基于脉间频率捷变的末制导雷达抗噪声调频干扰仿真研究

张永祥，顾晋晋

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

在现代战争中，战场环境日益复杂，精确制导武器可实现对敌目标的探测、截获、识别及跟踪，并能完成对敌目标的高精度打击，而成为战场上必不可少的作战手段[1-3]。末制导雷达作为精确制导武器实现高精度打击的核心部件，其作用就是完成导弹在运动过程中的末段制导工作[4]。因此，末制导雷达的电子对抗已成为军事战斗中常见的打击手段，且电子对抗手段随着干扰机技术及数字射频存储技术的发展而日益复杂[5-7]。

频率捷变技术是一种主动波形对抗技术，基于频率捷变的末制导雷达，因其载频不固定，所以可以自主规避噪声干扰频段，降低被侦察识别的概率[8-9]。国内科研工作者对频率捷变对抗的研究已取得了一定的成果。陈荣对频率捷变雷达在宽带阻塞干扰、频带边缘干扰等多种干扰形式下的干扰效果进行了分析[10]。刘天鹏、苏伍各等人，通过对脉间频率捷变雷达回波相位的分析，开展了雷达合成孔径雷达成像和逆合成孔径雷达研究[11-12]；张晨路等人对频率捷变雷达的3种(直接频率合成、光调制与光解调、直接数字式频率合成)信号接收方案进行了对比研究，并提出了相应的杂波抑制方案[13]。程彦杰等人研究了扫频干扰下频率捷变雷达的干扰效能及影响因素[14]。

针对末制导雷达的电子对抗，根据干扰产生方式的不同可分为无源干扰和有源干扰2种类型[15]。噪声调频干扰是有源干扰的一种，具有干扰频率涵盖范围大、带宽内变化较快的特点，在对敌方雷达目标进行干扰时，压制效果显著，遮盖明显。因此，噪声调频干扰被广泛应用[16]。

本文采用脉间频率捷变技术，实现末制导雷达对抗噪声调频干扰的目的。文中首先建立噪声调频干扰信号模型，然后对脉间频率捷变雷达模型进行分析，最后进行数值仿真。本文可为末制导雷达抗噪声干扰设计提供依据，对提高精确制导武器战场适应能力具有一定意义。

1 噪声调频干扰信号模型

在末制导雷达向目标发射脉冲信号时，假设目标只产生1个回波，目标回波信号S(t)可表示为[17]：

S(t)=ASe(t)

(1)

式中：A为回波幅度；Se(t)为发射信号包络，采用末制导雷达最常用的线性调频信号波形[18-20]，可表示为：

(2)

(3)

(4)

式中：f0为载频频率；T为脉冲宽度；μ为调频斜率；B为信号带宽。

仿真中，采用载频f0=18 GHz，信号带宽B=25 MHz，脉宽T=50 μs，雷达回波信号波形如图1所示。

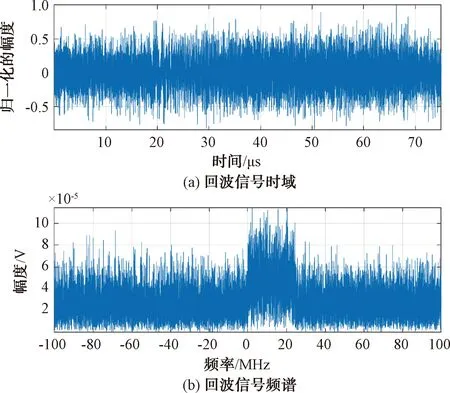
图1 目标回波信号波形

噪声调频干扰[21]为射频噪声干扰经频率调制后产生，噪声调频干扰J(t)可表示为：

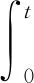
(5)

式中：U0为幅度；φ0为初始相位；ω0为中心频率；KFM为调频斜率；u(t′)为噪声调频信号。

噪声调频干扰的均值E[J(t)]可表示为：

E[J(t)]=U0Ecos[θ(t)+φ0]=0

(6)

θ(t)=ω0t+e(t)

(7)

(8)

噪声调频干扰的相关函数Rj(τ)可表示为：

(9)

当u(t′)服从均值为0的正态分布时，e(t)也服从均值为0的正态分布，则相关函数Rj(τ)为：

(10)

(11)

ΔΩn=2πΔfn

(12)

(13)

式中：σ2(τ)为调频函数方差;ΔΩn为调制噪声谱宽;mfe为有效调频指数;fde为噪声调频干扰信号有效调频带宽;Δfn为调制噪声带宽[21]。

噪声调频信号功率谱Gj(ω)的表达式为：

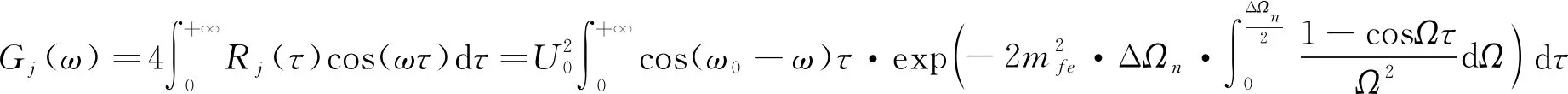
(14)

考虑到噪声调频干扰的功率谱Gj(ω)过于复杂，在分析噪声调频干扰时，一般根据有效调频指数mfe的设置条件求Gj(ω)近似解，具体为：

当mfe>>1时，Gj(ω)和噪声调频干扰等效带宽Δfj分别为：

(15)

(16)

当mfe<<1时，Gj(ω)和噪声调频干扰等效带宽Δfj分别为：

(17)

(18)

末制导雷达在与噪声调频干扰真实对抗中，一般采用mfe>>1情况，以获得较宽的噪声调频干扰等效带宽Δfj。噪声调频干扰信号的仿真结果，如图2所示。

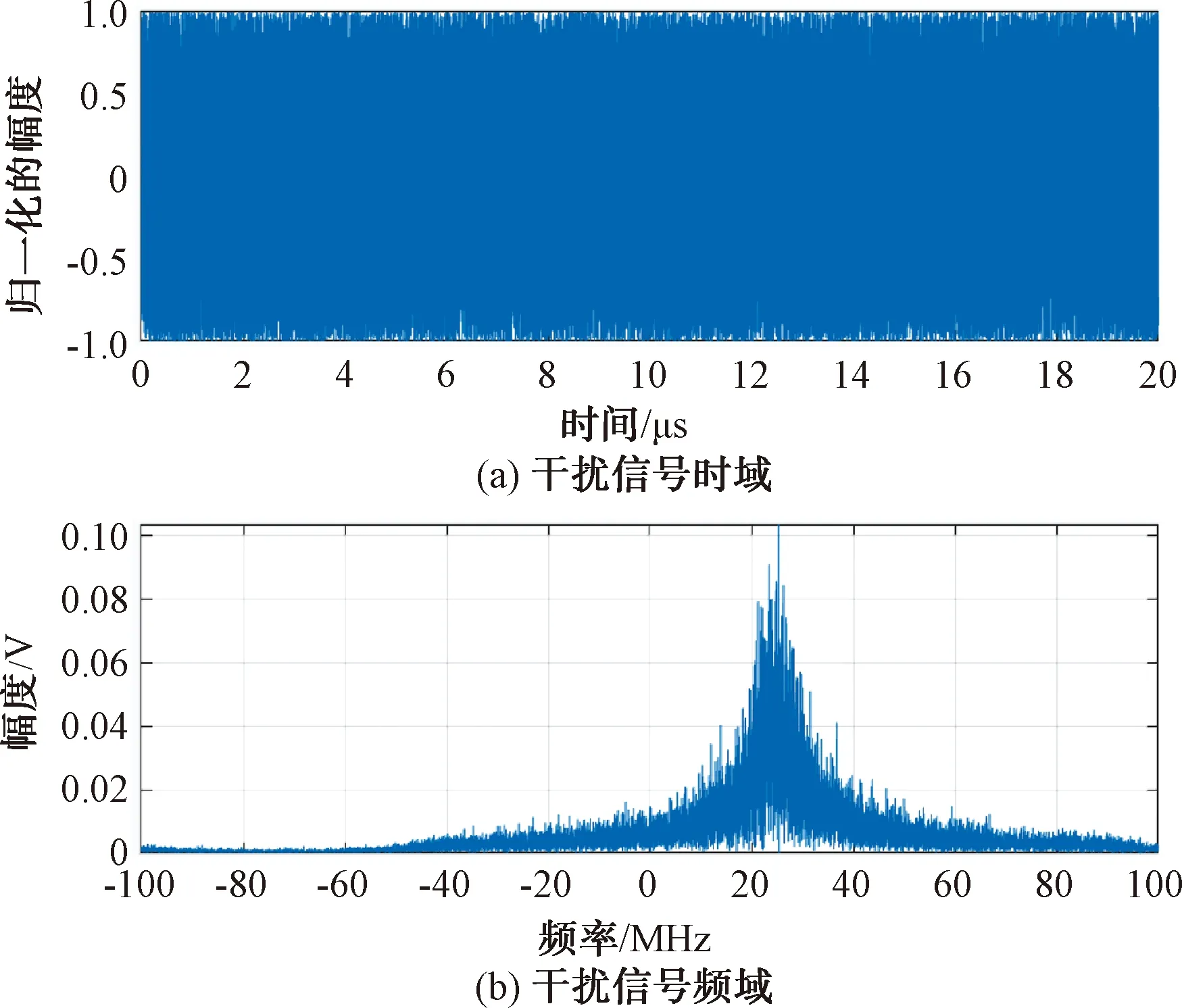
图2 噪声调频干扰信号仿真结果

2 脉间频率捷变雷达模型

脉间频率捷变是频率捷变方式的一种，基于脉间频率捷变的末制导雷达，其发射信号的载频均在宽带范围内，且载频按某种规律快速变化[9]。脉间频率捷变雷达发射信号Si(t)可表示为：

(19)

式中:Tr为信号的重复周期;T为脉冲宽度;μ为调频斜率;N为脉冲积累数目;fi为第i个脉冲的载波频率：

fi=f0+m(i)Δf,i=1,2,…,N

(20)

式中：f0为载频频率；Δf为相邻载频之间的频率间隔；m(i)为随机整数，取值范围为：

0≤m(i)≤M-1

(21)

式中：M为总的跳频数。

3 基于脉间频率捷变的末制导雷达抗噪声调频干扰仿真研究

在不考虑雷达噪声、环境噪声和杂波情况下，末制导雷达接收到的真实回波信号x(t)可以表示为：

x(t)=S(t)+J(t)

(22)

式中:S(t)为目标回波信号；J(t)噪声调频干扰。

仿真中，目标初始距离为60 km，仿真参数为载频f0=18 GHz，信号带宽B=25 MHz，脉宽T=50 μs，脉冲积累数目N=128，调制噪声带宽Δfn=50 MHz。

在末制导雷达发射信号经频率捷变处理前，对真实回波信号x(t)进行脉冲压缩处理，处理后的仿真结果如图3所示。由图3(a)可知，在无噪声调频干扰时，真实回波信号x(t)在60 km处被凸显；由图3(b)可知，在有噪声调频干扰时，目标被干扰信号覆盖。发射信号经频率捷变处理后，对末制导雷达的真实回波信号x(t)进行脉冲压缩处理，处理后的仿真结果如图4所示。由图4可知，经过频率捷变处理的发射信号，能够有效抑制噪声调频干扰，真实回波信号x(t)在60 km处被发现，噪声调频干扰无效。

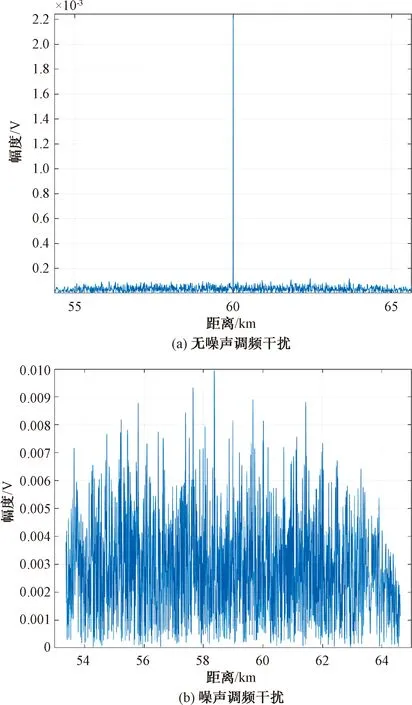
图3 发射信号经频率捷变处理前，对x(t)进行脉冲压缩处理的仿真结果

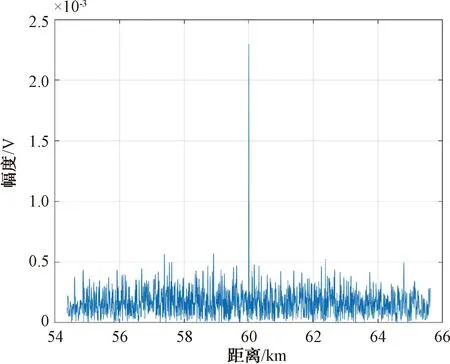
图4 发射信号经频率捷变处理后，对x(t)进行脉冲压缩处理的仿真结果

末制导雷达发射信号经频率捷变处理前后，测量距离与实际距离间的关系如图5所示，测量误差如图6所示。由图5和图6可知，在发射信号经频率捷变处理前，受噪声调频干扰影响，末制导雷达测距误差在-4～6 km之间，测距误差范围大，且分布杂乱；在发射信号经频率捷变处理后，制导雷达测量距离与实际距离几乎一致，测量效果不受噪声调频干扰的影响。仿真结果表明，基于脉间频率捷变的末制导雷达可有效抑制噪声调频干扰。

图5 末制导雷达发射信号经频率捷变处理前、后的距离测量曲线

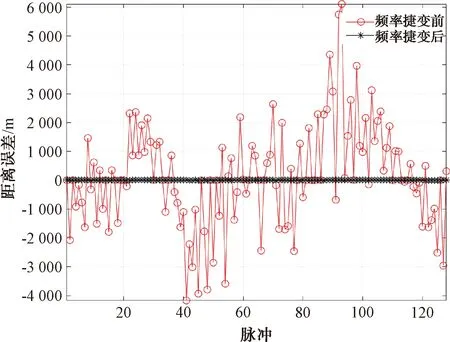
图6 末制导雷达发射信号经频率捷变处理前、后的距离测量误差曲线

4 结束语

本文就末制导雷达的电子对抗开展研究，首先建立了噪声调频干扰信号模型，然后建立脉间频率捷变雷达模型，最后仿真研究了末制导雷达在有无噪声干扰及频率捷变处理下的脉冲压缩处理结果、基于脉间频率捷变的末制导雷达的距离测量性能。仿真结果表明，脉间频率捷变抗噪声调频干扰措施有效。本研究内容可为末制导雷达抗噪声调频干扰的设计提供参考。