基于相位干涉法的反无人机系统的测向原理

2022-12-25徐后乐

舰船电子对抗 2022年6期

关键词：天线阵均匀分布接收机

徐后乐

(启元实验室，北京 100095)

0 引言

近20年来，随着无人机技术的发展，无人机技术正以革命性的进步解决现实生活中的各方面问题。并且市场规模也在逐渐稳步扩大，在国民经济和社会生产生活中发挥着越来越重要的作用。

目前无人机科技已应用于影视拍摄、飞行表演、快递运输、新闻报道、农业植保、灾难救援、野外监测、生物监控、测绘、电力巡检等多工作领域。

无人机技术将为企业和社会带来诸多好处。然而，从用户隐私和安全到法律问题和不公平使用，许多因素导致了无人机的劣势。

随着无人机的非法使用，对无人机的管控是相关部门必须要解决的问题。可以使用视频、雷达等技术手段来侦测无人机。然而视频技术由于受天气等影响不能全天候工作，而主动雷达由于需要发射电磁波来探测无人机，电磁波又会干扰电磁环境甚至危害人民群众的身体健康，所以被动无源雷达技术成为侦测无人机的主要手段。

无人机的方向或者具体位置是无人机管控需要的必要信息，无人机的测向技术是无人机管控必须要解决的问题。使用无线电检测无人机的方向属于无线电测向技术领域，无线电测向有比幅测向、相位干涉法测向、多普勒测向、空间谱估计测向等多种方法[1]。相位干涉法测向相比其他方法有测量精度高、工程实现简单等优点，因此相位干涉法普遍用于反无人机系统的测向。

天线阵的排列方式有多种方式，其中常用的有圆阵和L阵。多个天线阵均匀分布于一个圆阵中，称为均匀圆阵多元阵相位干涉测向；多个天线阵分布成L形，称为L阵多元阵相位干涉测向。其中均匀圆阵与L阵相比具有结构对称、精度高、灵敏度高等优点，所以常用的相位干涉法测向一般采用均匀圆阵结构。

本文首先推导了均匀圆阵的相位干涉测向的原理，然后利用MATLAB对算法进行了仿真，并实际采集无人机信号验证了该方法的正确性。

1 测向原理推理

如图1所示，N个全向天线阵均匀分布于圆心为O、半径为R的圆中，N个天线分别为A1,A2…An，其中A1位于x轴上，A1,A2…An逆时针排列。空中无人机M在圆阵的平面xoy的投影为P，水平角为α，俯仰角为β[2]。

图1 均匀圆阵相位干涉测向原理示意图

假设M到圆心O的距离为L，M的空间坐标为(xM,yM,zM),利用直角三角形的三角函数，可以得到如下公式：

(1)

(2)

xM=Lcosβcosα

(3)

yM=Lcosβsinα

(4)

zM=Lsinβ

(5)

N个天线均匀分布于半径为R的圆中，则天线An的方位角为：

(6)

其坐标为(xn,yn,zn),同理利用直角三角函数，可以得到：

xn=Rcosφn

(7)

yn=Rsinφn

(8)

zn=0

(9)

假设目标M的回波信号满足远场条件到达圆阵的N元阵天线，回波信号到圆阵圆心O点与天线An之间的距离差为Δdn，利用向量投影可以计算Δdn：

Rcosβcos(φn-α)

(10)

计算距离差Δdn带来的相位差为Δφn，要求Δdn小于回波信号的波长λ，则:

(11)

设n,m为N圆阵天线阵中的2个阵元的ID，根据式(11)可以得到回波信号到圆阵圆心O点与天线ID为n之间距离差引起的相位差:

(12)

同理，根据式(11)可以得到回波信号到圆阵圆心O点与ID为m的天线之间距离差引起的相位差：

(13)

设Δφn与Δφm的相位差为：

Δφn,m=Δφn-Δφm

(14)

即：

(15)

令：

cosαcosβ=x

(16)

sinαcosβ=y

(17)

将式(16)、(17)代入到式(15)中，从而得到：

(18)

令:

(19)

(20)

将式(19)、(20)代入到式(18)中，从而得到：

Δφn,m=an,m×x+bn,m×y

(21)

当N=5时，n分别取值为1～N，m取值为2，3,…,N,1时，利用式(19)和(20)可得如下表达式：

(22)

(23)

(24)

对于式(22)的求解，利用最小二乘法可以计算出x和y的值[3]，即:

(25)

不难发现，式(17)除以式(16)可得:

(26)

根据式(26)可以得到目标的方位角:

(27)

将式(16)、(17)代入下式可得:

x2+y2=(cosαcosβ)2+(sinαcosβ)2=cos2β

(28)

从而得到目标的俯仰角：

(29)

利用该方法可以得到目标的俯仰角，但是不能够区分无人机是在圆阵的上方还是下方。如果想要确定无人机在天线阵的上方还是下方，需要利用2层天线阵即可实现。如果没有这方面的需求，只需要一个均匀分布于一个圆阵的多元天线阵加相关的无线电接收设备即可精确探测出无人机的来波方向。

2 天线阵参数

均匀圆阵相位干涉法测向中天线阵的主要参数是圆阵的半径，根据上面的算法原理推理可知，计算无人机的来波方向需要测量2个天线阵的回波信号的相位差公式Δφn,m。在实际工程实现时，2个天线阵的回波信号的相位差的最大值与最小值之间的差要小于等于1个周期，即360°，因此要求：

|Δφn,m|≤π

(30)

将式(15)代入式(30)，可得：

n-m=1

(31)

表1列出了第2节中天线阵元在相关频率下的天线阵半径。

表1 不同阵元下的天线圆阵半径参数

3 测向算法仿真

为了验证上述相位干涉法测向原理的正确性，采用MATLAB程序对该算法进行仿真。先假设在理想情况下，各个天线阵的接收机幅度和相位完全平衡，模拟无人机的方位角和俯仰角分别为49.5°和11°，为了计算无人机到各个天线阵之间的相位差，仿真程序除了设定无人机角度信息外，还需要设定无人机距离天线阵中心的距离。该仿真程序对天线阵进行了100次数据采集,并计算无人机的角度信息。由于仿真是基于理想情况进行的，所以计算出的角度信息与仿真程序的设置值一致，该程序验证了上述相位干涉法测向算法的正确性，仿真结果如图2所示。

图2 理想情况下相位干涉法测量无人机角度信息的仿真结果

实际情况下，由于模拟元器件以及线长不严格等长等因素导致各个天线到接收机的模数转换器(ADC)之间的物理链路不完全一致，因此多个接收通道之间存在幅度和相位不平衡，假设各个通道之间的相位差在[-5°,5°]范围内符合均匀分布，重新对上面的仿真程序进行仿真，仿真结果如图3所示。仿真结果表明，虽然各个通道存在相位不一致性，但是通道间的相位差在一定范围内，该算法也可以比较准确地解算出无人机的角度信息。

图3 幅相不一致时相位干涉法测量无人机角度信息的仿真结果

4 工程验证

在室外，利用无人机对测向算法进行工程验证，天线采用五元阵天线。为了节省接收机通道，使用具有2个接收通道的接收机，天线阵与接收机之间采用射频切换开关实现2个接收通道的接收机对多个天线阵分时采集，每次同时采集相邻2个天线之间的回波数据。接收机的硬件架构如图4所示。

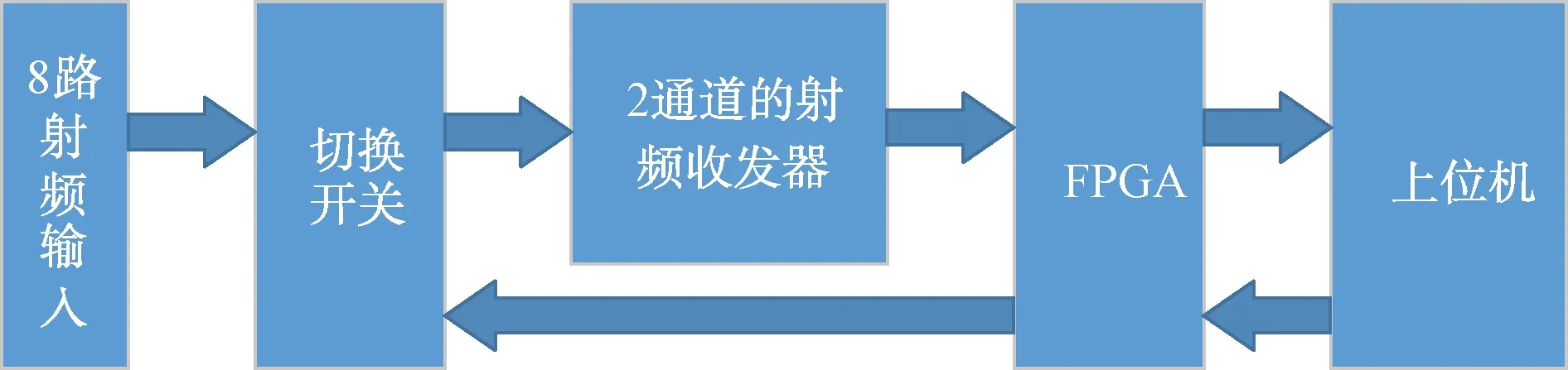
图4 多通道接收机的硬件框架

现场可编程门阵列(FPGA)将同时采集到的2个通道的原始数据通过PCIE发送给上位机，上位机将收到的数据保存成文件。连续地依次采集多个相邻天线阵对之间的数据，并一直不断地循环。MATLAB读取上位机保存的回波数据，并进行信号处理，图5是100帧某个相邻天线对的回波信号的频谱瀑布图，将2个天线的回波信号瀑布图分别显示在图的左右两侧。

图5 相邻天线对的实际回波信号的频谱瀑布图

MATLAB先读取上位机保存的数据文件，判断相应的帧标志后，读取各个天线对的原始数据，并对数据进行幅相校正，然后进行快速傅里叶变换(FFT)计算频率，再估计无人机信号的频带，在目标频带内计算天线对的相位差，通过相位差可以得到式(24)的矩阵B，根据式(19)和(20)可以得到式(23)的矩阵A，然后将矩阵A和B代入到式(25)可以得到x和y，将x和y代入到式(27)和(29)，可以得到无人机的水平角和俯仰角。图6是使用实际采集无人机的回波数据，然后根据本论文的测向算法100次计算无人机的角度信息。该图表明多次测量无人机的角度信息，水平角在3°范围内波动，俯仰角在3°范围内波动，相位干涉法测量无人机的角度波动小，可靠性高。