通信发射系统中各种因素对EVM指标的影响
2022-12-25王平
王 平
(中国电子科技集团公司第三十六研究所,浙江 嘉兴 314033)
0 引 言
误差矢量幅度(EVM)是衡量一个通信发射系统性能的重要指标[1]。
EVM定义了时域上数字调制信号与理想信号的精度误差[2],如图1所示。实测信号矢量S(n)与理想信号矢量R(n)之间的夹角为相位误差;S(n)与R(n)之间的幅度差为幅度误差;S(n)与R(n)之间的矢量差即为误差矢量E(n)。

图1 误差矢量图
EVM表示误差矢量幅度相对理想矢量幅度的百分比,计算公式如下:
(1)
EVM是在一定时间内,理想无误差信号与实测信号的向量差。因为在每个符号变化时,这个值也在不断变化,所以EVM值存在最大值、均方根值(RMS)等多个概念。一般情况下,采用EVM的均方根值来表示。EVM值越大,说明发射系统发射信号的调制质量越差;EVM值越小,发射信号调制质量越好,表明发射的信号越接近于理想信号。理解EVM定义以及分析其与系统设计指标参数的关系,对于通信发射系统的设计、开发是极其关键的。
1 各种因素对EVM指标的影响分析
在通信发射系统中,信号从产生到发射的流程如图2所示。

图2 通信发射系统信号流程示意图
首先,数字基带I/Q信号通过数字正交上变频产生数字射频信号S(t),信号的时域表达式为:
S(t)=I(t)cos(ωct)+Q(t)sin(ωct)
(2)
式中:基带信号I(t)和Q(t)包含了调制信息;ωc=2πfc表示射频的载波角频率。
数字射频信号S(t)通过数模转换(DAC)得到模拟信号S1,之后再通过信号调理或者模拟上变频得到最终的射频小信号S2,信号S2经过功率放大器设备产生射频待发射信号S3,最后通过发射天线辐射出去。
一般情况下,通信发射系统产生并发射的数字调制信号会遇到多种失真因素,导致信号调制有误差,EVM指标恶化。失真因素包括:I/Q不平衡、相位噪声[3]、非线性放大[4]、信道加性高斯白噪声[5]等。
1.1 I/Q不平衡
在发射机中,I/Q不平衡指发射机的同相(I)和正交(Q)支路间的幅度和相位不匹配。理想情况下,同相和正交支路具有相等的幅度增益和90°相位偏差。但是在实际的发射系统中,通常难以实现上述理想情况。非理想的上变频、I和Q支路的不平衡滤波器和数模转换器(DAC)等均可能产生I/Q不平衡。
以正交相移键控(QPSK)信号为例,I/Q不平衡对此信号EVM指标影响的仿真模型图如图3所示。在仿真模型中,EVM模块的参考输入为理想的QPSK信号,实际输入为经过I/Q不平衡模块后的QPSK信号。
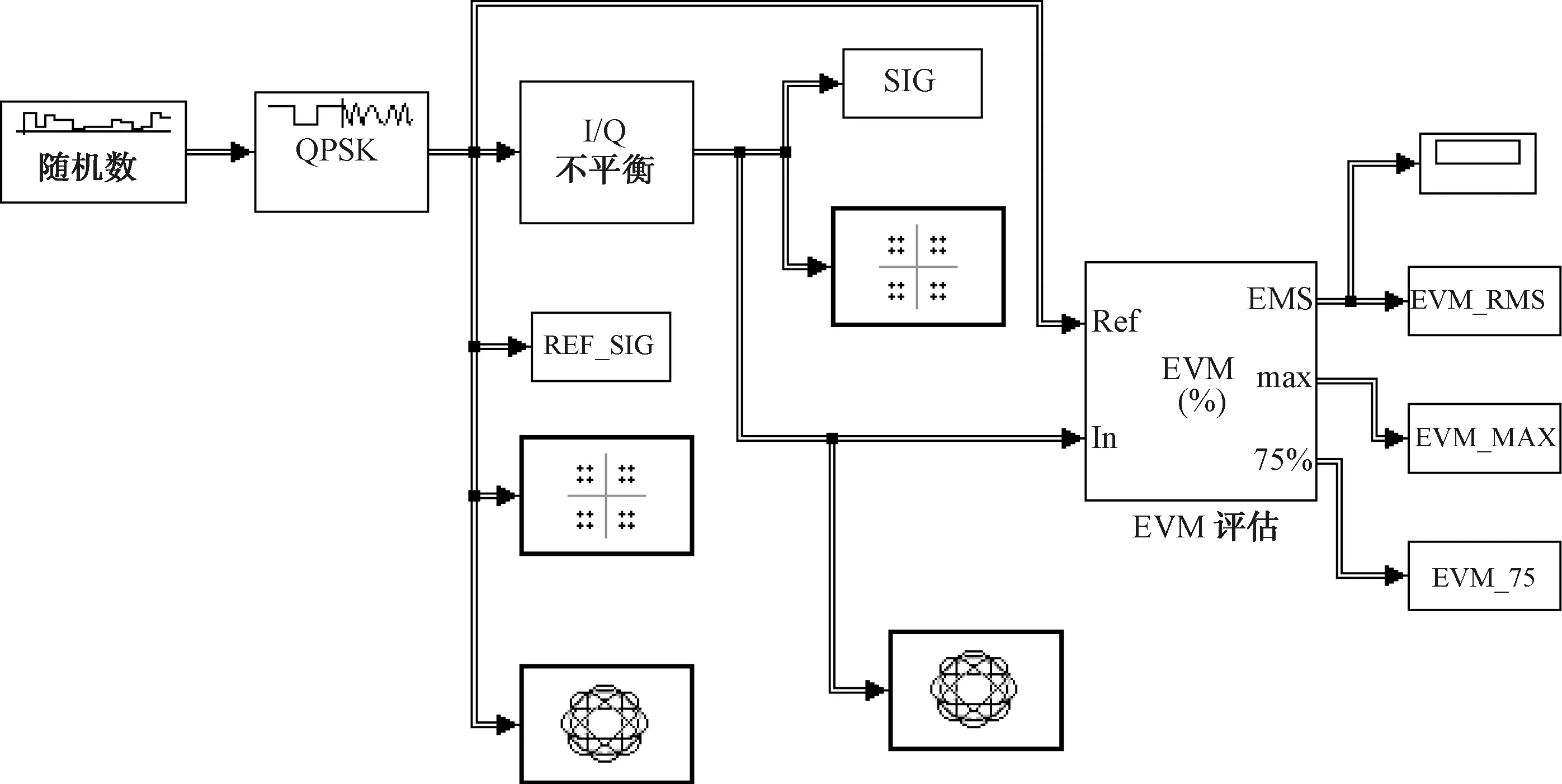
图3 I/Q不平衡对QPSK信号EVM指标影响的仿真模型图
I/Q不平衡包括I/Q幅度不平衡和I/Q相位不平衡,通过设置IQ不平衡模块中的具体参数来进行仿真。I/Q幅度不平衡达到2 dB时,仿真的EVM均方根为11.56%,对应的信号星座轨迹对比图如图 4 所示,可以发现此时信号的矢量星座点已经发生了明显的偏移,星座轨迹已经明显变形。

图4 I/Q幅度不平衡信号与理想信号的星座轨迹对比图
改变参数值,不同程度的I/Q幅度不平衡对应的EVM值如表1 所示。
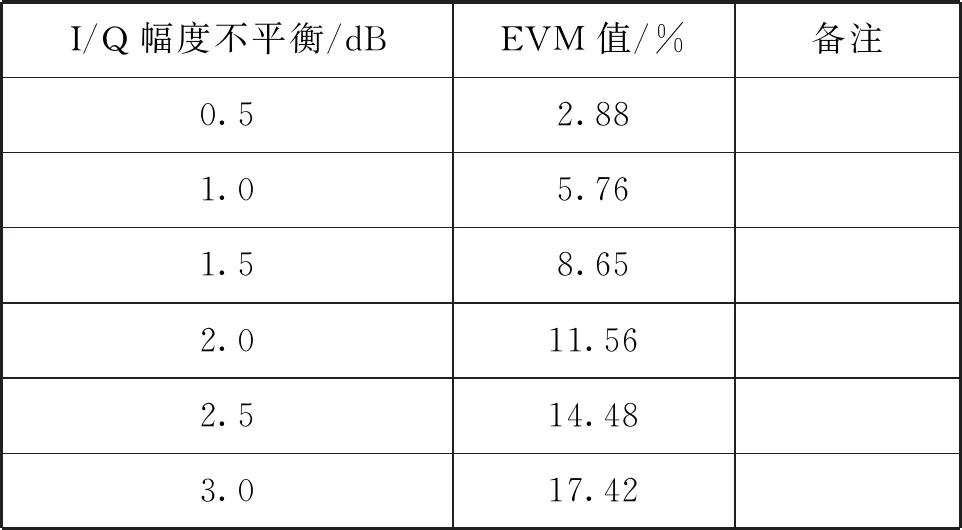
表1 不同程度I/Q幅度不平衡对应的EVM值
I/Q相位不平衡达到12°时,仿真的EVM均方根为10.51%,对应的信号星座轨迹对比图如图5所示。此时信号的矢量星座点已经发生了明显的扭曲。
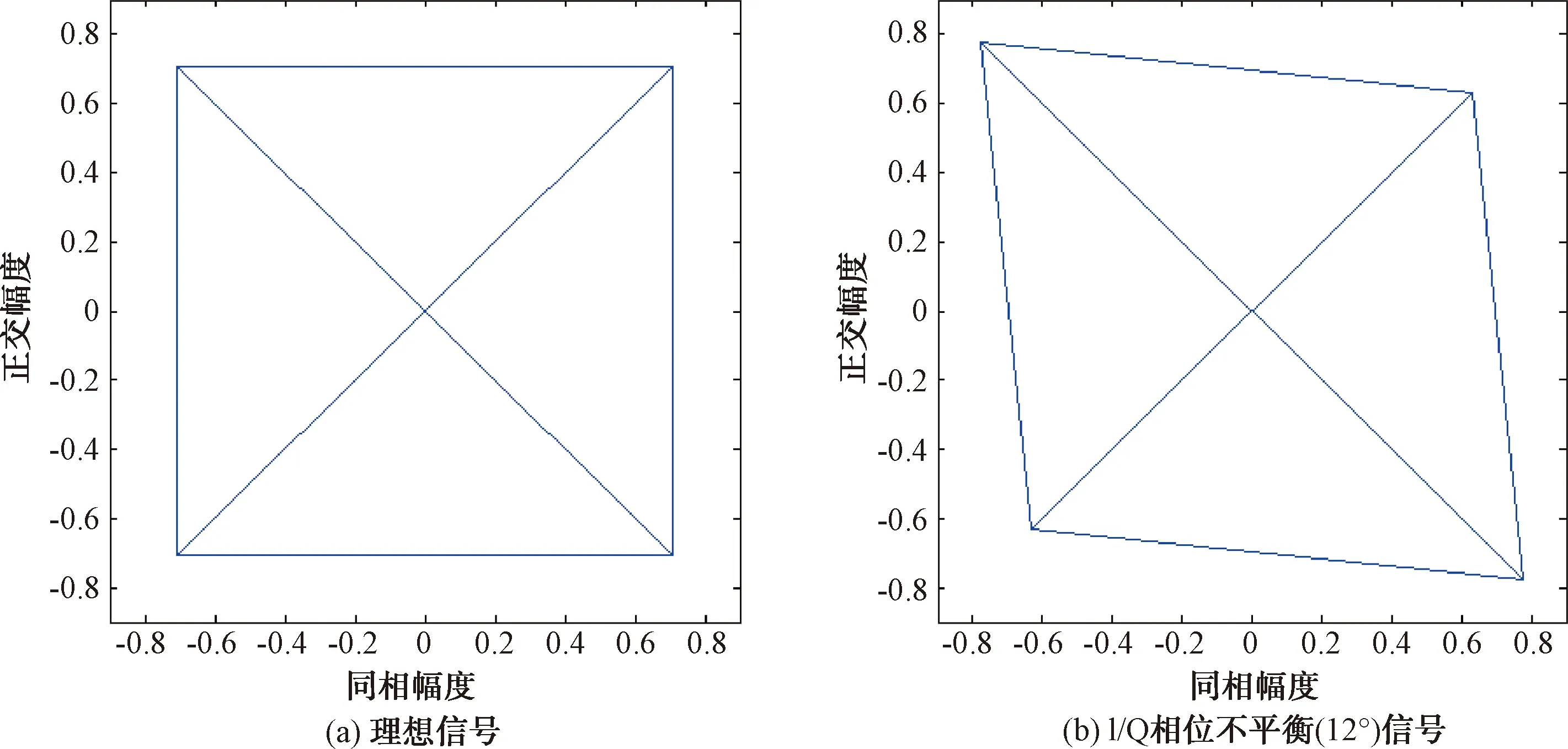
图5 I/Q相位不平衡信号与理想信号的星座轨迹对比图
改变参数值,不同程度的I/Q相位不平衡对应的EVM值如表2所示。

表2 不同程度I/Q相位不平衡对应的EVM值
I/Q幅度不平衡和I/Q相位不平衡叠加后,对应的EVM值如表3所示。
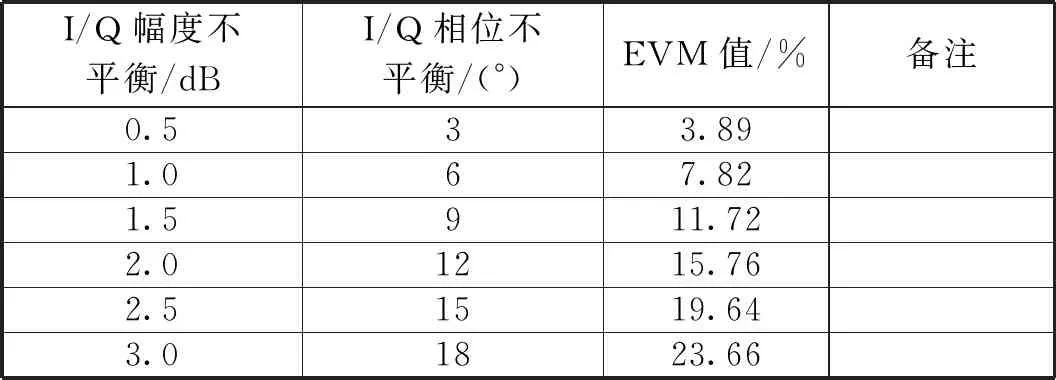
表3 不同程度I/Q不平衡对应的EVM值
可见,I/Q不平衡越明显,对应的EVM值越大,信号质量越差。
1.2 相位噪声
在发射机中,本振信号的相位噪声是一种常见的噪声,在时域上表现为抖动,在频域上表现为宽裙边。相位噪声对QPSK信号EVM指标影响的仿真模型图如图6所示。
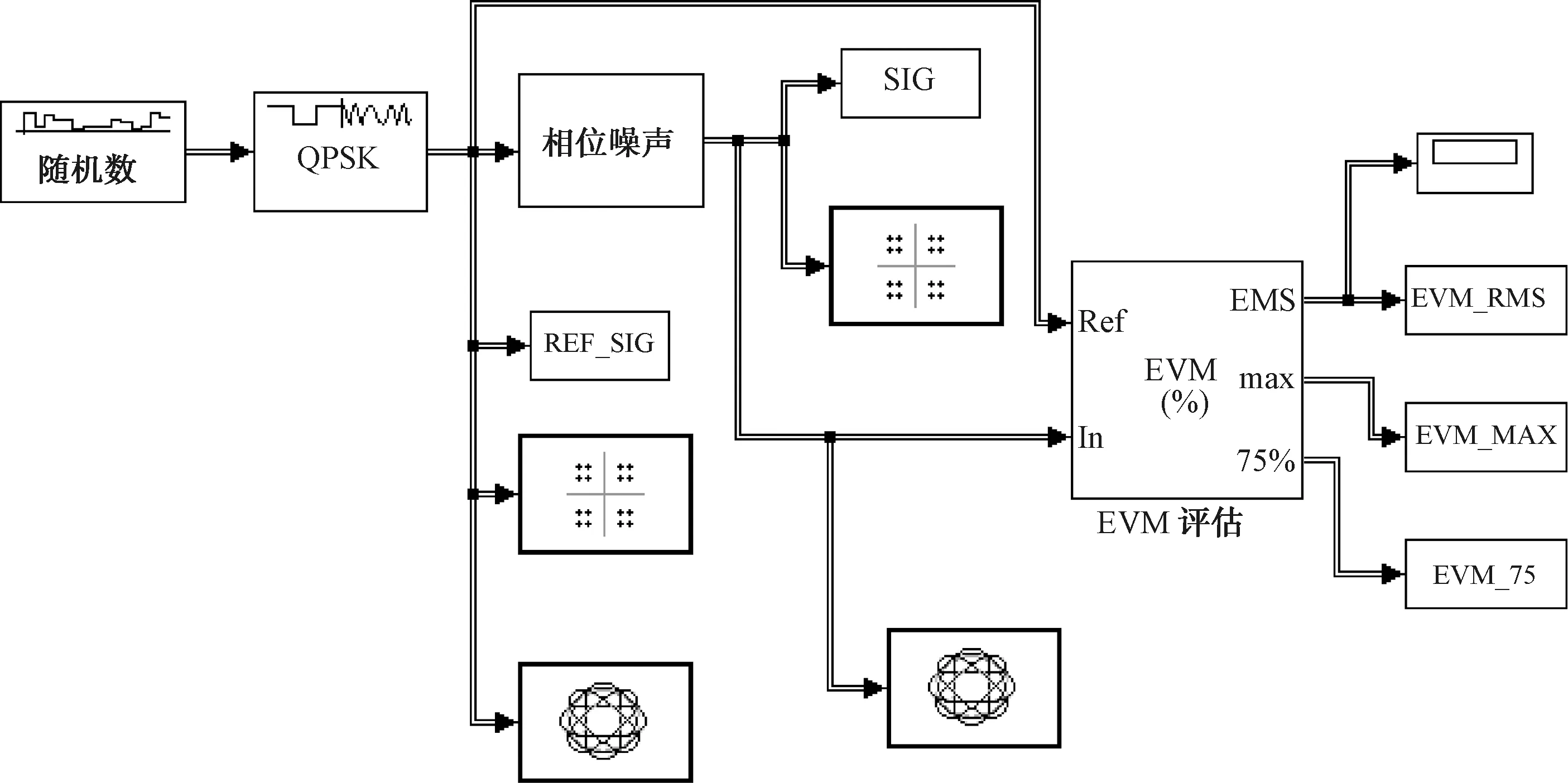
图6 相位噪声对QPSK信号EVM指标影响的仿真模型图
相位噪声为-80 dBc/Hz(频谱10 kHz)时,仿真的EVM均方根为4.72%,对应的信号星座轨迹对比图如图 7 所示,此时信号的矢量星座点已经发生了明显的扩散和旋转。
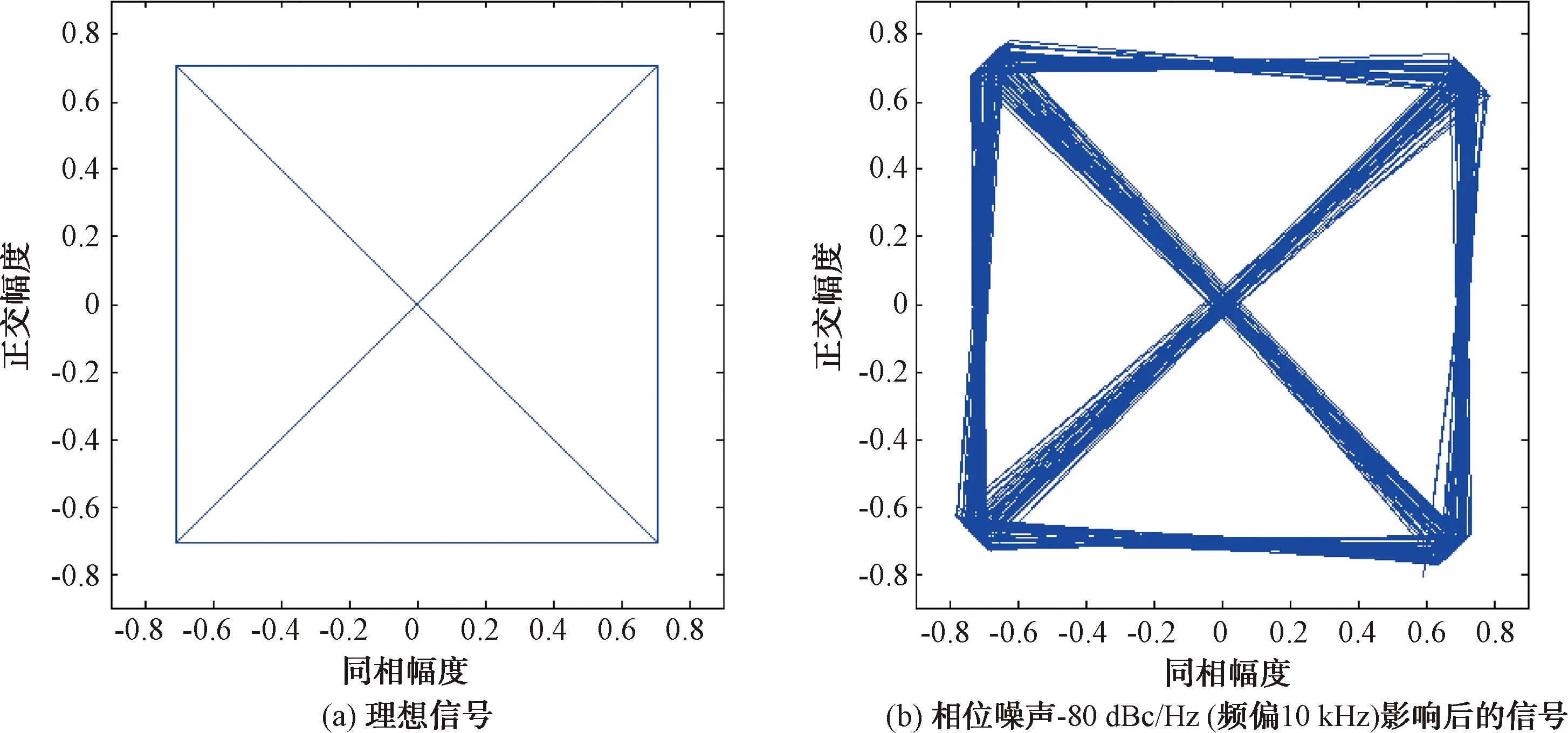
图7 相位噪声影响后的信号与理想信号的星座轨迹对比图
在频偏为10 kHz的情况下,不同相位噪声对信号EVM值的影响如表4所示。
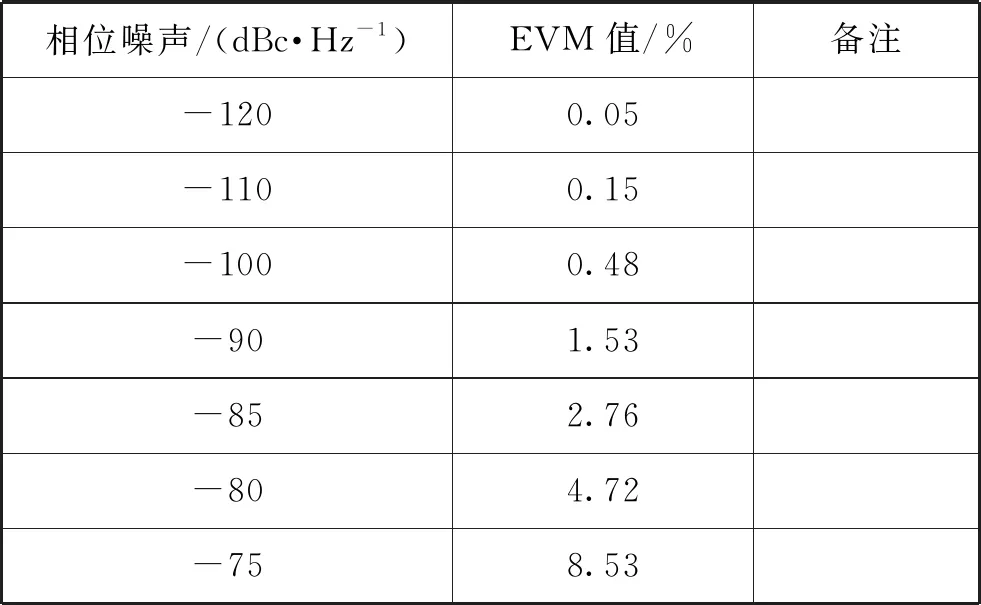
表4 不同相位噪声下信号的EVM值
可见,相位噪声指标越恶化,对应的EVM值越大,信号质量越差。
1.3 非线性放大
在发射信号的产生、放大和传输过程中,非线性放大主要由功率放大器产生。因为实际使用的功率放大器为非线性器件,并且功率放大器的效率越高,其非线性程度一般也越差。在发射系统中,为了获得较高的效率,功率放大器一般工作在AB类,工作点在1 dB压缩点附近,甚至在饱和区,此时的非线性效应将更加严重。
功率放大器的非线性主要体现在2个方面:AM-AM特性和AM-PM特性。其中AM-AM特性表示输出信号幅度和输入信号幅度的关系,AM-PM特性表示与输入信号幅度相关的输出信号的附加相移。现假设输入到功率放大器的等效复信号为:
Vi(t)=r(t)ejθ(t)
(3)
式中:r(t)和θ(t)分别为输入信号Vi(t)的幅度和相位。
功率放大器的输出信号为:
Vo(t)=G(r(t))ej(θ(t)+Φ(r(t)))
(4)
那么,G和Ф就分别称为功率放大器的AM-AM和AM-PM特性函数。AM-AM特性使得功率放大器的输出不再是其输入的线性函数,产生幅度失真。AM-PM特性使得输出的信号附加相移不为零,相当于存在一个调相分量,产生相位失真。
同样以QPSK信号为例:产生8个信号频率为100~117.5 MHz(频率等间隔2.5 MHz)、符号速率均为1 Msps的 QPSK小信号,然后通过某型最大输出500 W的功率放大器设备。对放大后中心频率为115 MHz的QPSK信号进行解调和EVM实测,功率输出50 W时,实测结果如图 8 所示,EVM值为14.59%。

图8 功率放大器放大后QPSK信号的实测解调图
改变功率放大器的输出功率,对应的EVM值如表5 所示。

表5 不同功率放大时信号的EVM值
结论:功率放大器输出功率越大,非线性越严重,对应的EVM值越大,信号质量越差。
1.4 信道加性高斯白噪声
噪声是所有通信信道的固有部分,实际的噪声信号在某一频段内可以用高斯白噪声的特性来进行近似处理。信道加性高斯白噪声(AWGN)是一个数学模型,可用于仿真发射机与接收机之间的信道噪声。
信道加性高斯白噪声对QPSK信号EVM指标影响的仿真模型和图6类似,只是将相位噪声换成了AWGN。
信道加性高斯白噪声的信噪比为22 dB时,仿真的EVM均方根为7.96%,对应的信号星座轨迹对比如图9所示,此时信号的矢量星座点已经发生了很明显的扩散。
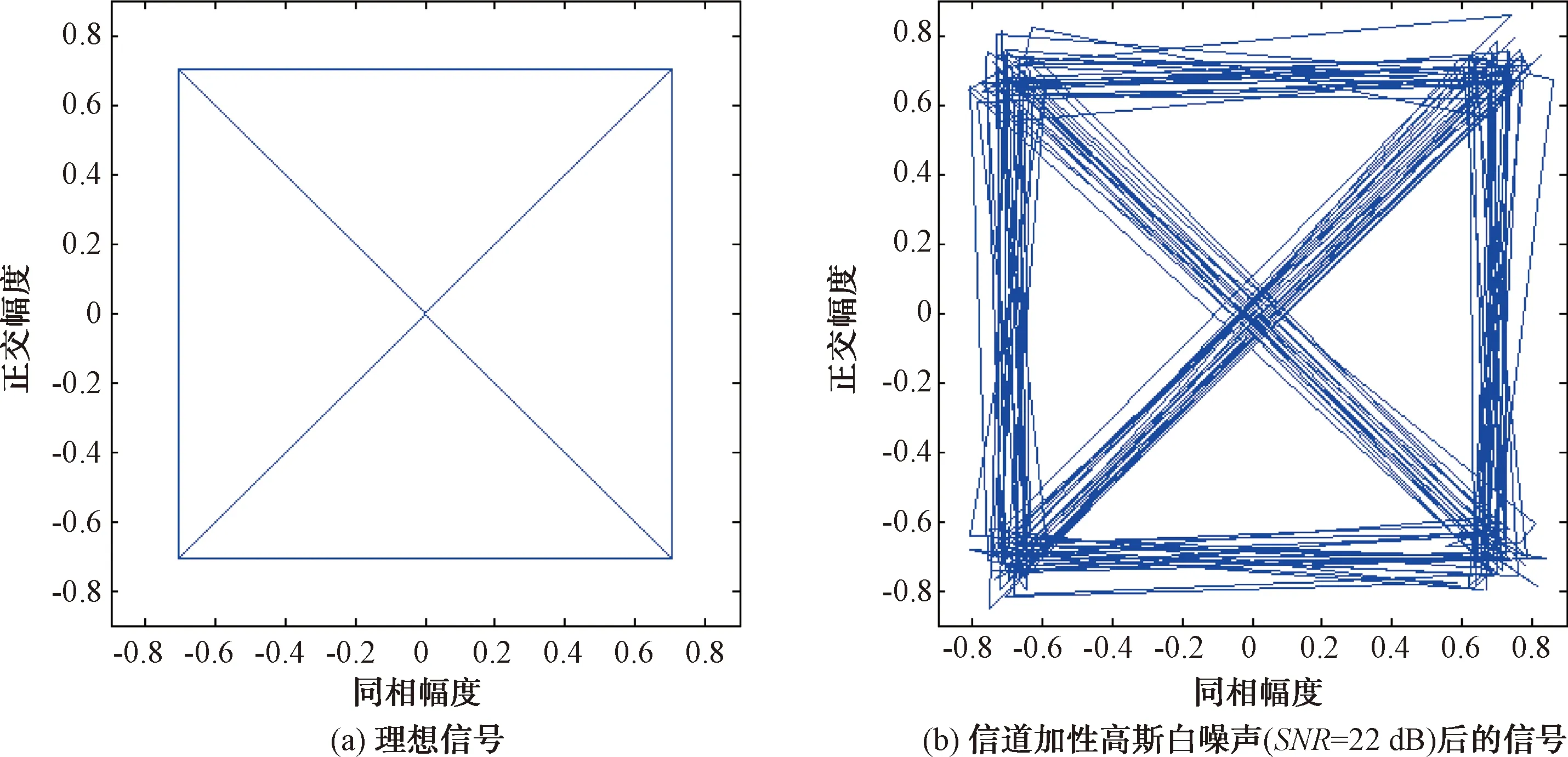
图9 信道加性高斯白噪声后的信号与理想信号的星座轨迹对比图
不同信噪比的加性高斯白噪声对信号EVM值的影响如表6所示。
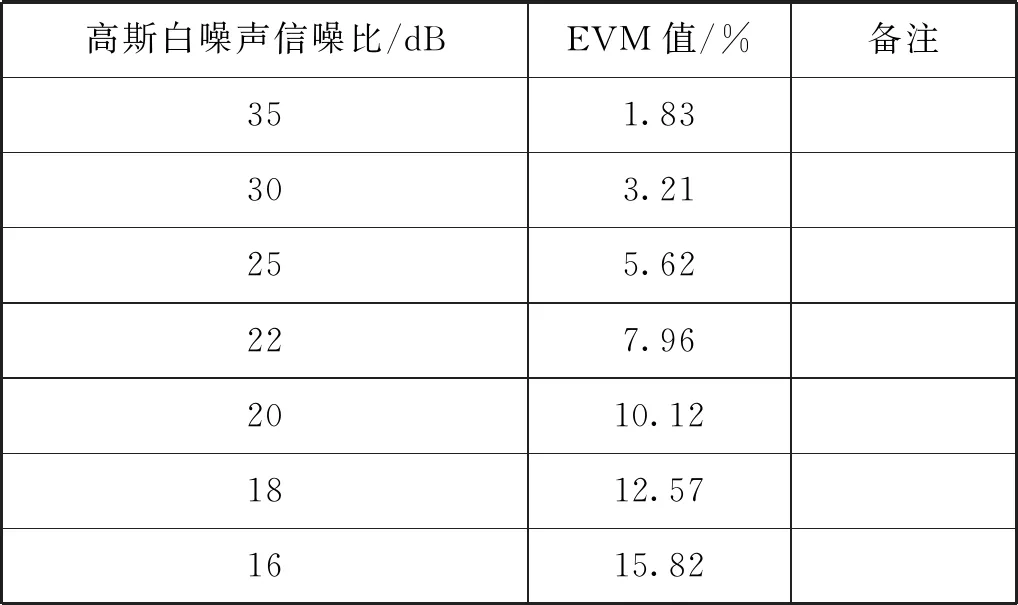
表6 增加不同信噪比的高斯白噪声后信号的EVM值
结论:信道加性高斯白噪声的信噪比越低,对应的EVM值越大,信号质量越差。
2 结束语
在通信发射系统中,I/Q不平衡、相位噪声、非线性放大和信道加性高斯白噪声都会对数字调制信号的EVM指标产生影响。除此之外,如果在信号
产生的过程中,采用了软件削波或者硬件限幅等有损信号处理,那么最终信号的EVM指标势必也会随之恶化。
本文都是以QPSK调制信号为例进行的仿真计算或实测,但不同阶调制信号的抗干扰能力不一样,数字调制信号调制方式越复杂,频率带宽利用率越高,抗干扰能力越差。根据3GPP技术规范TS38.141的参考规定,QPSK的EVM指标要求为18.5%以内,四进制正交幅度调制(16QAM)的EVM指标要求为13.5%以内,八进制正交幅度调制(64QAM)的EVM指标要求为9%以内。因此,在实际工程中,一方面要尽可能优化各种设计来降低EVM指标;另一方面也要根据情况综合选择合适的信号调制阶数。
