基于间歇采样的LFM雷达干扰建模与仿真

崔 伟，魏 杰，王琰琦

(1.空军航空大学，吉林 长春 130022；2.解放军93841部队，新疆 乌鲁木齐 830037)

0 引 言

随着对抗新体制雷达的需求牵引，基于数字射频存储器(DRFM)的干扰技术得到了长足发展，尤其针对线性调频脉压信号更能获得良好的干扰效果。间歇采样转发技术能够实现对大带宽信号的实时性干扰，灵巧噪声可以产生高密度的脉内相参假目标，均可有效对抗脉内和脉间调制的雷达波形[1-3]。文献[4]～[6]提出了非均匀间歇采样转发干扰的形式，运用m序列产生多普勒频移调制和延时非均匀转发等方式实现非均匀间歇采样，并使用禁忌搜索算法进行优化求解，改善了均匀采样方式的不足。文献[7]对卷积调制的灵巧噪声进行了建模与仿真，并研究了干扰效果。文献[8]提出了灵巧噪声干扰机的组成原理。文献[9]建立了时域卷积及乘积调制灵巧干扰的通用数学模型，具有较强普适性。文献[10]～[13]分别以三角波、方波、梯形波和梳状谱作为卷积调制信号，并分析了干扰效果。文献[14]对几种不同卷积调制干扰样式进行了归纳与对比。文献[15]进一步提出多波形调制的干扰机架构，增强了干扰的应用性与针对性。然而，现有的干扰应用仍具有一定局限性：如非均匀采样方式干扰效果单一、可控性差，复杂的内部调制削弱了间歇采样转发干扰的实时性等。

本文基于间歇采样和卷积调制灵巧噪声的建模与分析，提出了一种周期交替采样的非均匀采样方法，能够实时产生人工可控的假目标群；进一步提出锯齿波卷积调制的干扰信号形式，并与间歇采样转发相结合，产生了非均匀的密集假目标群，压制和遮盖效果均较强；通过调整周期锯齿波的各项参数可以实现假目标的位置、幅度和密度的灵活控制，针对性强，对雷达的自适应干扰具有重要意义。

1 干扰信号建模与分析

1.1 间歇采样与匹配滤波

假定采样脉冲信号形式如下：

(1)

式中：τ为脉宽;Ts为重复周期;fs为采样频率，通过傅里叶变换得到其频谱为：

(2)

设雷达发射LFM脉冲信号x(t)，经间歇采样后得到采样信号为：

xs(t)=q(t)x(t)

(3)

其频谱为：

Xs(f)=Q(f)*X(f)

(4)

代入式(2)得：

(5)

式中：Xs(f)为X(f)的周期加权延拓；fs为延拓周期；an=τfsSa(nπτfs)，代表幅度加权系数。

设h(t)为雷达接收机匹配滤波器响应函数，经匹配滤波后，采样信号输出为ys(t)，其表达式为：

ys(t)=xs(t)*h(t)

(6)

其频谱为：

Ys(f)=Xs(f)H(f)=

(7)

式中的X(f-nfs)H(f)可视为多普勒频移为fd=nfs的回波经匹配滤波后输出的频谱，则Ys(f)可看成具有不同多普勒频移的回波脉冲信号经匹配滤波并幅度加权后频谱的叠加。

结合前面对an的分析，对于线性调频(LFM)雷达，干扰效果表现为一个幅度较大的主假目标(对应于n=0时)和位于其两侧幅度逐渐衰减的假目标群(对应于其他情况下)。

1.2 锯齿波卷积调制

设计卷积调制信号为周期锯齿波，设置锯齿波幅值为1，周期为T，其表达式为：

(8)

对其进行傅里叶级数展开：

(9)

(10)

(11)

(12)

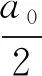
将各参数代入式(9)得：

(13)

其频谱为：

(14)

干扰信号经匹配滤波后可表示为：

xp(t)=x(t)*f(t)*h(t)

(15)

其频谱为:

XP(ω)=|X(ω)|2F(ω)

(16)

经上述分析可知，F(ω)集中分布于零点附近，频谱形式表现为一系列冲击函数，其幅度由零点向两侧逐渐减小。由此可知，经卷积调制后的干扰频谱集中在线性调频信号的中心频率附近且其幅度向两侧逐渐降低。

2 间歇采样转发干扰效果分析

2.1 均匀间歇采样

假设线性调频信号带宽为15 MHz，时宽为50 μs，信号时频域特性如图1所示。

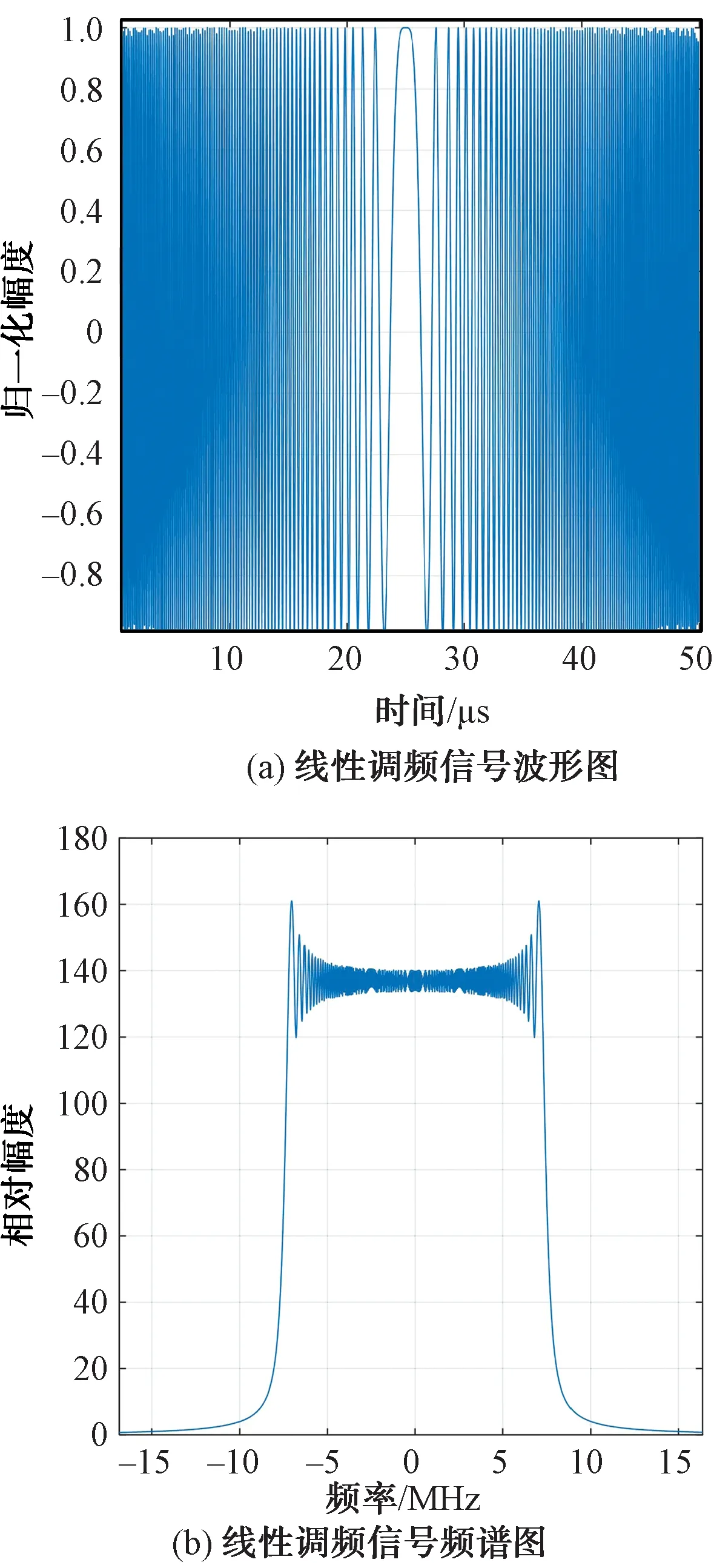
图1 线性调频信号时频特性图

对其进行均匀间歇采样处理，设置采样周期为4 μs，采样脉宽为2 μs，仿真结果如图2所示。

图2 间歇采样信号时频特性图

为分析参数变化对干扰效果的影响，分别设置Ts为4 μs、2 μs，τ为2 μs、1 μs，仿真结果如图3所示。

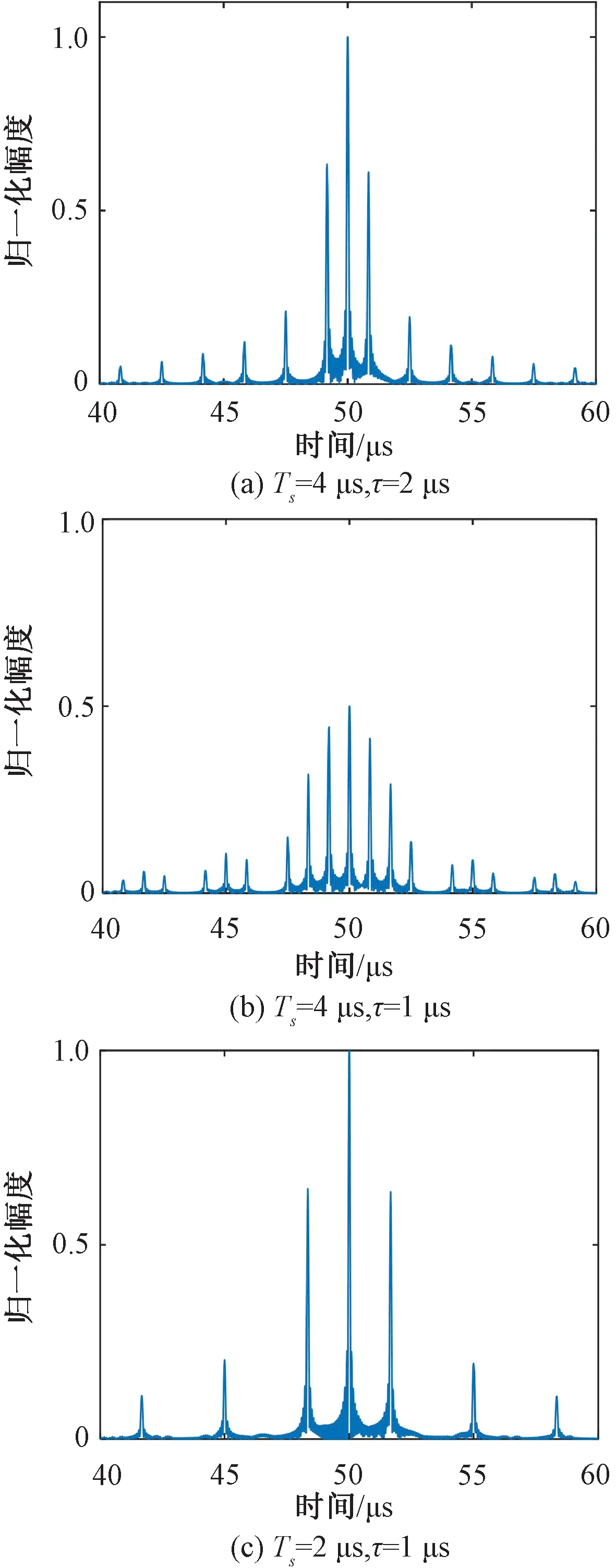
图3 不同参数下干扰信号波形图

由图3可知，均匀采样转发干扰效果表现为一串径向分布的假目标串，主假目标幅度最高，次假目标幅度由中心主假目标向两侧逐渐衰减，有效假目标个数为3～5个。

结合图3与前面对an的分析可知，假目标幅度取决于采样占空比，占空比越大，主假目标幅度就越高。直接转发条件下，50%为可实现的最大占空比，随占空比减小，次假目标衰减速度减缓，形成的假目标群幅度相差不大。占空比不变，Ts增大时，各假目标的间距减小，分布更加密集。

2.2 周期交替采样转发干扰

结合前面仿真结果可知，均匀采样转发干扰具有有效假目标个数较少、压制效果弱、规律性强等缺陷，在参数设置上也往往顾此失彼，干扰效果不明显。对此，提出一种周期交替采样的新方式，该方式自主设置不同的采样参数交替循环执行，不同采样参数和周期次序所产生的干扰效果也不同。

此处以三周期交替采样为例，设置间歇采样周期分别为4 μs、6 μs和3 μs，对应占空比设置为50%、20%以及40%，在雷达信号时宽内按次序循环进行采样，仿真结果如图4所示。

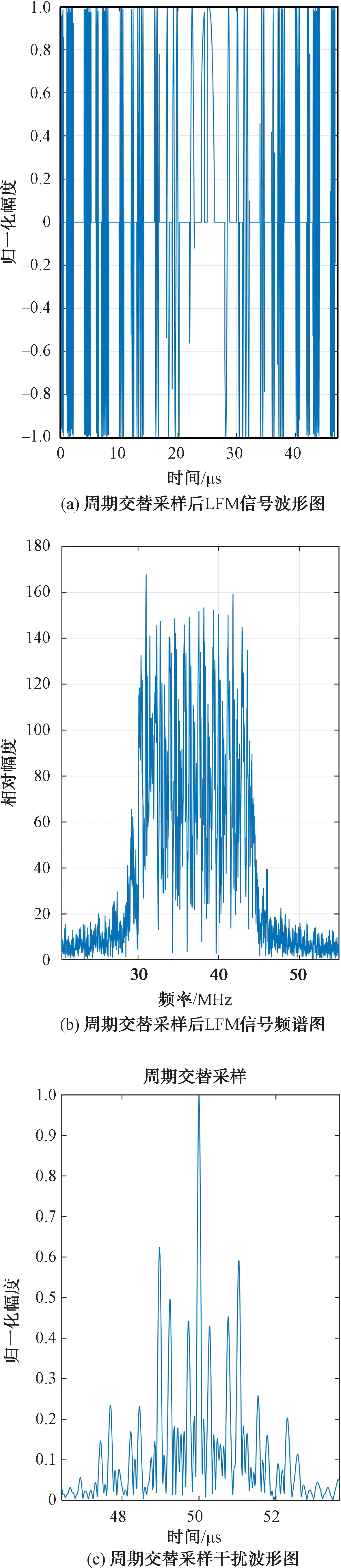
图4 周期交替采样信号时频特性及干扰波形图

与均匀采样方式相比，周期交替采样方式有效假目标数量及密集程度增加，假目标群整体幅度有较大提升且分布更为随机，压制干扰效果更加明显。通过合理搭配不同采样参数及周期交替次序，可以使假目标幅度、密集程度及衰减速度等参数更具针对性，干扰效果灵活可控，较好地解决了均匀采样方式的不足。

3 卷积调制灵巧噪声

3.1 锯齿波卷积调制干扰

以锯齿波作为卷积调制信号，设置锯齿波频率为1 MHz，采样率15 MHz，周期为1 μs，噪声时宽为5 μs，即以5个周期为对象，仿真得到干扰信号匹配滤波输出如图5所示。

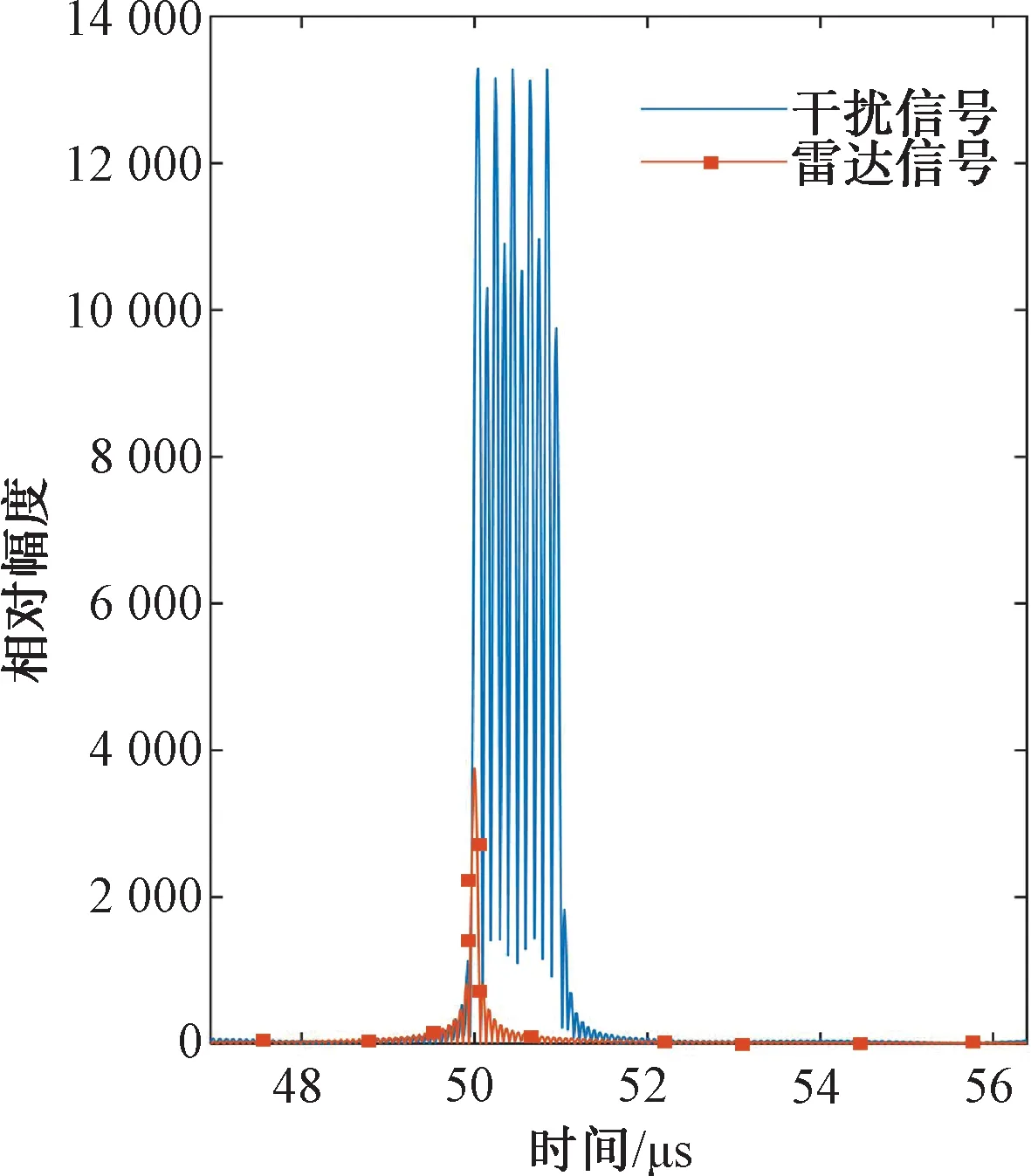
图5 锯齿波卷积调制干扰匹配滤波输出

经匹配滤波后，干扰生成5个主假目标，其幅度相比于真实信号有大幅提高，假目标属性可以灵活控制，假目标群具备欺骗和遮盖双重效果。

3.2 基于间歇采样的锯齿波卷积调制干扰

(1) 基于不同采样方式的锯齿波卷积调制干扰

锯齿波参数设置同上，噪声时宽为7 μs，均匀采样周期4 μs，占空比50%，三周期交替采样周期分别为1 μs、3 μs和2 μs，占空比对应为50%、40%、40%。仿真结果如图6所示。

图6 不同采样方式下干扰信号匹配滤波输出波形图

经卷积调制后，周期交替采样产生的主假目标幅度较之均匀采样有一定提高，两种采样方式总的干扰效果相似，改善了单一干扰样式规律性、延时性等缺陷，集群假目标欺骗及遮盖效果更好。

(2) 参数分析

以均匀采样方式为例，对锯齿波频率、时宽等参数变化带来的影响进行具体分析。

设置锯齿波频率f分别为1 MHz、0.5 MHz，采样率fs分别为15 MHz、20 MHz，噪声时长Ls分别为5 μs、15 μs，间歇采样周期4 μs，占空比50%。仿真结果如图7所示。

由图7可知：随噪声时宽Ls增加，假目标群幅度提高，并随之出现一定时延，随采样率fs提高，干扰信号幅度得到较大的提升，然而假目标覆盖范围缩减，随锯齿波频率增大，假目标分布更为密集，而其幅度产生衰减。

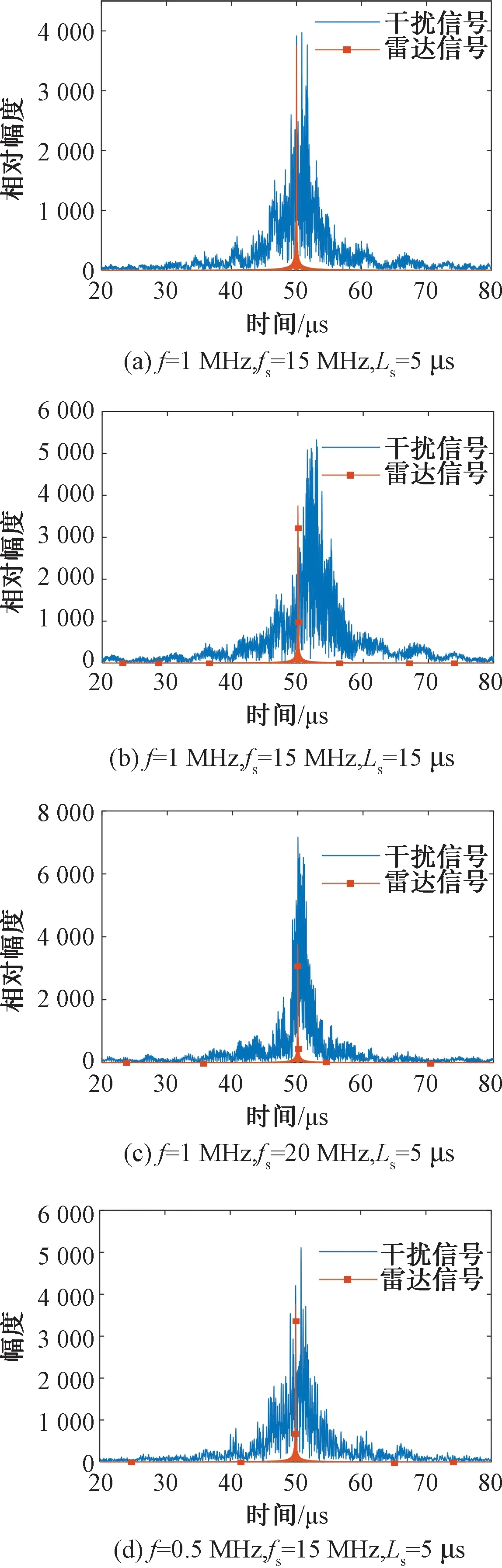
图7 参数变化对干扰效果的影响图

仿真结果证明，通过调节周期锯齿波各时域参数，可以控制假目标位置、幅度以及密集程度等属性，干扰效果灵活可控。通过合理配置有关参数，有利于针对特定雷达信号实施最佳干扰，对干扰机的自适应干扰技术具有重要意义。

4 结束语

基于均匀采样转发样式，提出了周期交替采样的方式，假目标群整体幅度提升且分布随机，压制干扰效果明显改善，干扰效果灵活可控。并以噪声卷积调制为基础，提出了锯齿波卷积调制的干扰信号形式，进一步在均匀及非均匀间歇采样的基础上进行锯齿波卷积调制，产生了具有非均匀密集假目标性质的灵巧干扰，欺骗和遮盖效果强。通过调整周期锯齿波的各项参数可以实现假目标的位置、幅度和密度的灵活控制，对雷达干扰具有适应性、针对性。