基于ANSYS软件的1+6钢丝绳网格划分策略及仿真
2022-12-25韦磊,张鸿
韦 磊,张 鸿
(中国船舶集团有限公司第八研究院,江苏 扬州 225101)
0 引 言
钢丝绳具有质量轻、承载大、工作平稳等特点,广泛地应用于各种工业场合,运输领域的港口集装箱吊装设备、建筑领域的塔式起重机、机械领域的车间行车、生活中的电梯无不彰显钢丝绳的优势。钢丝绳由于具有复杂的螺旋捻制结构,内部钢丝之间存在非线性接触特征,常规的理论计算无法准确获取钢丝绳内部的力学和运动特性,因此本文主要借助有限元仿真软件ANSYS对其进行研究。ANSYS有限元软件广泛应用于机械领域,不仅能够进行简单的静力学仿真计算,还能够进行非线性的力学仿真求解[1]。本文主要针对1+6钢丝绳进行研究,具体分析钢丝绳有限元建模方法和钢丝绳内部钢丝受力和运动情况。该研究方法对于复杂的异形股、多层股等不同类型的钢丝绳同样适用。
1 1+6钢丝绳有限元模型
1.1 三维模型导入
1+6钢丝绳具有螺旋捻制特征,其侧丝的几何生成曲线含有一次螺旋线[2],如图1所示。ANSYS软件中直接建立螺旋结构体较为麻烦,因此可以借助三维软件Creo2.0进行建模。将Creo2.0软件中建立的钢丝绳的三维模型保存为igs格式,应用ANSYS软件中的/AUX15接口导入到ANSYS软件进行分析。由于1+6钢丝绳具有对称性结构,只需要导入钢丝绳内部中心丝和1根侧丝,通过VGEN体复制命令可以得到完整的1+6钢丝绳。为了方便在ANSYS软件中提取钢丝绳内部钢丝接触线上的位移特征,研究钢丝之间的相对运动,在Creo2.0软件中绘制出钢丝接触线[3],导入ANSYS软件后则会自动生成接触线。本文选用的1+6钢丝绳参数如下:中心丝丝径3.4 mm,侧丝丝径3.1 mm,侧丝捻距73 mm,钢丝绳长100 mm。

图1 1+6钢丝绳三维模型
1.2 网格划分策略
ANSYS软件中常用的网格划分方法有自由网格划分和映射网格划分。这2种网格划分方法对钢丝绳进行网格划分都不能在钢丝接触位置准确地生成节点。为了节约非线性计算的时间,在不影响研究数据可靠性的前提下更快更准确地得到计算结果,本文采用分层切割且网格密度渐变的网格策略进行网格划分。钢丝绳轴向两端存在约束及边界效应,因此主要对钢丝绳轴向中间段进行研究,中间段需要网格细化。同时钢丝绳内部中心丝和侧丝接触位置存在应力集中,因此中心丝与侧丝的线接触位置需要进行网格细化。
下面具体说明1+6钢丝绳在ANSYS软件中的网格划分策略:
(1) 使用VSBW体切割命令切割钢丝绳,通过移动工作平面将整绳切割得到3段钢丝绳,进而将每段钢丝绳沿轴向采用不同的网格密度进行划分;
(2) 选用MESH200单元对钢丝绳端面进行网格划分,在中心丝和侧丝接触位置生成节点,将端面钢丝接触位置的网格进行细化,提高求解精度,如图2所示;

图2 1+6钢丝绳端面网格模型
(3) 使用LESIZE命令控制钢丝绳轴向网格划分密度,通过设定合适的比例尺,中间段沿轴向采用一致较密的网格划分,两侧沿轴向采用两端渐疏的网格划分,如图3所示;

图3 1+6钢丝绳轴向网格模型
(4) 选用185单元对钢丝绳进行体网格划分,使用VSWEEP体扫掠命令进行钢丝的体扫掠从而生成体网格。
通过上述网格划分策略获得的网格模型不仅在1+6钢丝绳内部中心丝和侧丝接触线上准确生成节点且接触线位置的网格得到细化,钢丝绳轴向中间段的网格也进行了精细划分,因此通过ANSYS软件计算得到的钢丝绳中间段和接触线上的节点数据更加准确。而钢丝绳两端面受边界效应影响较大,选择较为稀疏的网格密度划分,在不影响求解精度的前提下缩短了求解时间。
1.3 接触、约束施加与求解
接触问题的求解首先需要满足接触条件,具体包括法向接触条件和切向接触条件,其中法向接触条件为不可贯入性和法向接触力为压力,切向接触条件本文考虑有摩擦的库伦模型[4]。不可贯入性可以表示为:
(1)
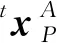
库伦摩擦模型可以表示为:
(2)
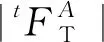
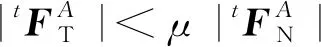
1+6钢丝绳的中心丝和6根侧丝之间相互接触,需要在ANSYS软件中定义接触对,具体通过定义目标单元和接触单元来实现。TARGE170单元可以表示三角形、圆柱形、圆锥形、球形等多种形式的复杂曲面形状,选用TARGE170作为目标单元,三维4节点低阶四边形CONTA173单元可以定义柔性三维的接触面,选用CONTA173作为接触单元。通过设置合适的关键字选项和实常数可以定义钢丝间的接触特性,关键字设置如下:
KEYOPT(2)=0,设置摩擦类型KEYOPT(12)=0,通过设置摩擦系数MU的数值来定义摩擦系数。TARGE170与CONTA173需要设置的具体实常数包括法向接触刚度(FKN)、最大穿透容差(FTOLN)、初始接触调整带(ICONT)、指定近区域接触范围(PINB)等。实常数设置如下:FKN=0.5,FTOLN=0.01,ICONT=0,PINB=0.5。
钢丝绳主要载荷形式为拉伸载荷,本文主要研究拉伸位移载荷下1+6钢丝绳的应力分布和运动分析。本文钢丝绳边界约束条件为一端固定,另一端施加位移载荷,具体操作过程如下:
选取固定端面的所有节点,对其施加完全约束,即可将钢丝绳的一侧端面固定;在钢丝绳加载端面上方1 mm处建立参考节点,选取参考节点和加载端面上的所有节点,耦合这些节点所有方向的自由度,实现参考节点和加载端面的刚性化,对参考节点施加载荷可以等效为对加载端面加载。加载端面具有x、y、z3个方向的移动、转动自由度,因此参考节点可以选用质量21单元。本文对参考节点施加位移载荷0.2 mm,控制参考节点z向的转动自由度可以实现钢丝绳加载端面约束扭转和自由扭转2种不同的边界约束。本方法通过对参考节点定义边界条件和施加载荷可以实现对加载端面的等效操作。
通过有限元软件对钢丝绳进行非线性接触求解,很多学者为了使求解更快地收敛,忽略内部钢丝之间的摩擦,将摩擦系数设为0。本文考虑摩擦的影响,设置摩擦系数为0.115。同时考虑Von Mises屈服准则,设置材料屈服极限为1 500 MPa。将有限元软件的程序单位均使用kN、cm进行输入,得到的应力单位为107Pa。
2 1+6钢丝绳应力分布及运动分析
2.1 1+6钢丝绳应力分布
1+6钢丝绳中间段受边界约束效应影响较小,因此取出z=50 mm的中间截面进行分析,分别得到约束扭转和自由扭转时中间截面的等效应力云图,如图4所示。
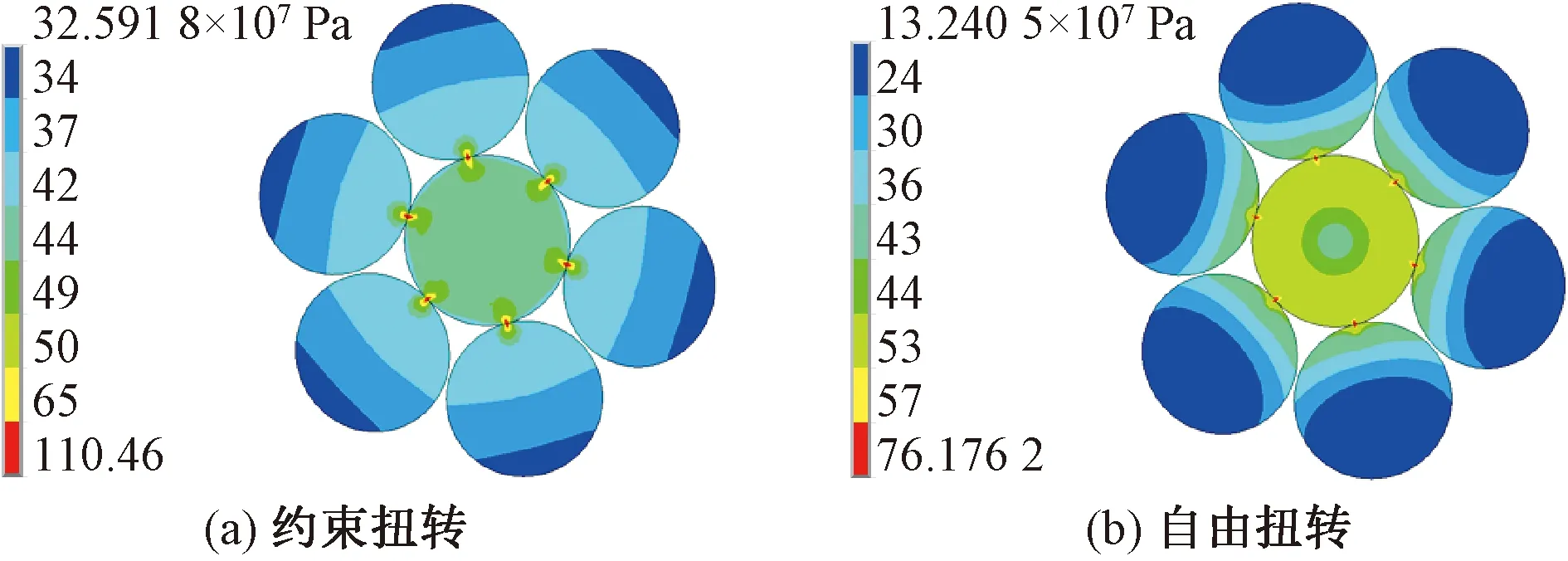
图4 中间截面的等效应力云图
从图4所示的应力云图可以看出,约束扭转和自由扭转2种边界约束条件下,两者等效应力均在中心丝与侧丝的接触位置达到最大值,同时约束扭转时等效应力在数值上明显大于自由扭转。这是由于约束扭转情况下内部应力得不到有效释放,而自由扭转下钢丝绳一端可以自由旋转,从而释放了一部分的应力。2种约束边界条件下侧丝的应力变化梯度均比中心丝的应力变化梯度更加明显,中心丝的等效应力由接触位置处向中心处逐渐降低,而侧丝的等效应力由接触位置向侧丝外圈快速衰减,其中约束扭转下侧丝等效应力接近层状分布,自由扭转下侧丝的等效应力接近于二次曲线状分布。
2.2 1+6钢丝绳运动分析
为了清晰地反映钢丝绳截面上的位移分布情况,取出钢丝绳z=50 mm的中间截面进行分析,将结果坐标系设置为Global cylindric,钢丝绳在约束扭转、自由扭转时中间截面的各向位移分布云图分别如图5、图6所示。
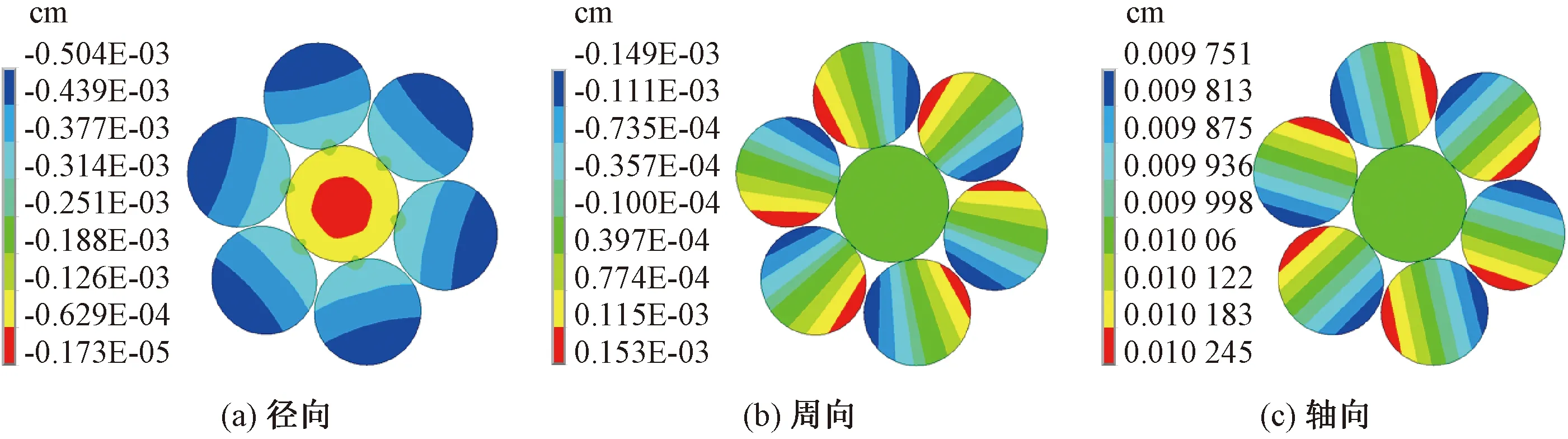
图5 约束扭转时中间截面各向位移分布
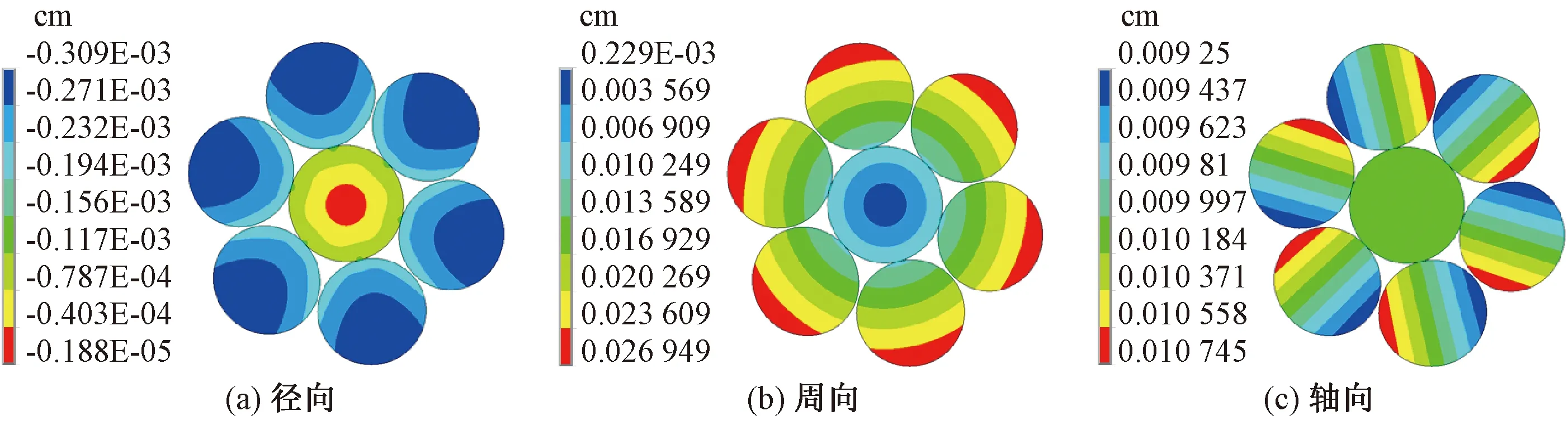
图6 自由扭转时中间截面各向位移分布
从截面的各向位移分布图可见,中心丝径向位移分布在约束扭转和自由扭转时相同,由内向外逐渐增大,周向位移在约束扭转时接近于0,自由扭转时由内向外呈环状逐渐增大,轴向位移在约束扭转和自由扭转时相同,接近0.01 cm;侧丝径向位移分布在约束扭转时接近层状分布,自由扭转时呈二次曲线状分布,由接触位置向外逐渐增大,周向位移在约束扭转时接近层状分布且接触位置接近于0,自由扭转时呈二次曲线状分布且由接触位置向外逐渐增大,轴向位移在约束扭转和自由扭转时均呈层状分布。
1+6钢丝绳内部中心丝和侧丝的接触线为一次螺旋线,施加轴向位移载荷时,中心丝和侧丝会产生相对运动,钢丝间相对运动状态可以通过钢丝间接触线的各向相对位移来描述。
通过网格划分策略可以在接触线上生成节点,提取接触线上节点的坐标和各向位移,可以拟合出完整的接触线的运动轨迹。由于提取接触线上各节点在笛卡尔坐标系下的位移很难描述中心丝和侧丝的相对运动状态,因此提取接触线上各节点在柱坐标下的运动位移,1+6钢丝绳内部中心丝与侧丝的相对运动主要通过周向相对位移和轴向相对位移体现。约束扭转和自由扭转时1+6钢丝绳中心丝(IW)和侧丝(OW)接触线的周向相对位移和轴向相对位移沿钢丝绳轴向的变化如图7所示。
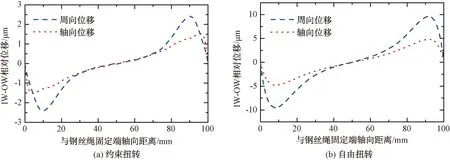
图7 接触线相对位移
约束扭转和自由扭转时1+6钢丝绳两端面的中心丝和侧丝没有相对运动,因此周向相对位移和轴向相对位移均为0。侧丝由于具有螺旋捻制特性,在受到拉伸位移载荷的情况下会与中心丝产生相对转动。周向相对位移和轴向相对位移在中间段基本上呈线性变化,钢丝绳自身具有对称性,z=50 mm处的周向相对位移和轴向相对位移为0,而钢丝绳两端面由于边界约束发生突变,自由扭转时周向相对位移和轴向相对位移均大于约束扭转的情况。
3 结束语
本文建立了基于ANSYS软件的1+6钢丝绳有限元模型,提出了一种分割渐变的网格划分策略,对需研究位置的网格进行细化,实现了钢丝绳非线性求解的精确性和快速性。求解得到约束扭转和自由扭转2种约束条件下1+6钢丝绳的应力云图,约束扭转时等效应力在数值上明显大于自由扭转。同时求解得到约束扭转和自由扭转2种约束条件下1+6钢丝绳的中间截面各向位移分布和接触线的周向、轴向相对位移沿轴向的变化,自由扭转时周向、轴向相对位移在数值上明显大于约束扭转。
