精心设计课堂导入 深化数学概念教学

徐 彬

江苏省常州市戚墅堰实验中学 213011

数学概念涵盖了数学的公式、定义、法则和定理等内容，是数学知识的核心和基础，是解决数学问题的基石，因此数学概念教学在数学教学中具有至关重要的作用.在概念教学中，教师容易犯照本宣科的错误，或者采用强行记忆的教学方式，导致学生不能真正理解数学概念的内涵，出现记忆混淆、概念错用的现象.在进行概念教学时，教师要通过教学活动引导学生参与体验，让学生不仅知其然，更知其所以然，真正理解概念的形成过程，从而更好地运用数学概念解决问题，促进数学思维的发展［1］.在概念教学中，科学合理地进行导入可以有效提升概念教学的有效性，能激发学生的学习兴趣和求知欲.笔者平时对数学概念教学的导入进行了一些实践和思考，下面谈谈自己的想法.

联系生活导入新概念

概念的形成不是空洞的说教，需要建立在学生已有的生活经验基础之上.因此，进行概念教学的导入时，教师要联系学生已有的生活经验，让学生观察和分析生活中熟悉的事例，以激发学生的好奇心.学生通过寻找生活中的原型，更能在直观感性认识的基础上学习概念.

案例1正、负数.

教学时，教师可通过生活中大量有相反意义的生活用语进行导入，如收入和支出、上升和下降、零上和零下等，这样能让学生更加轻松地认识正、负数所代表的意义.

案例2数轴.

数轴概念的导入也可以从学生熟悉的生活入手.

（1）首先，学生可以根据地图画出自己家到学校的路程，并通过自己的生活体验，感受到路程问题可以简化为具体的直线问题，从而进行研究.

（2）其次，教师可以让学生在直线的相应位置画出相对应的物体，使学生初步感知“数轴”的概念.

（3）最后，教师可以让学生观察温度计，比较温度计与自己所画图形的区别.通过观察，学生发现温度计上的温度有0刻度以上和0刻度以下之分，它们可分别用正数和负数表示，从而引出“数轴”的概念.

温故知新导入新概念

类比是数学学习中的重要方法之一，其可以起到温故知新、锻炼思维、构建知识框架的作用.类比不仅是调动思维进行前后知识联系和比较，从而更加深入学习的一种思维锻炼手段，还是进行概念引入的一种重要方法.

案例3圆周角.

学生已经学习了圆心角，在此基础上学习圆周角的概念时，教师可以采用与圆心角类比的方法进行导入.

师：我们已经知道圆心角是顶点在圆心的角，那么圆周角有什么特点呢？

生（齐）：圆周角一定是顶点在圆周的角.

师：老师画几个角，同学们判断一下这些角是不是圆周角（如图1所示）.

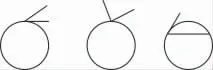
图1

（学生陷入沉默）

师：仅仅是顶点在圆周上的角就一定是圆周角吗？

生（齐）：不一定.

师：除了顶点在圆周上，在判断圆周角时，我们还要看角的两边的位置.那么为什么圆心角的定义只要规定角的顶点就可以了呢？

通过与所学知识进行类比，学生可以轻松地掌握新的知识，并能区分圆周角和圆心角之间的异同点，在轻松的氛围中自然而然地接受了新的概念.

设置问题导入新概念

思维是数学的核心，在概念教学中同样要注意思维的训练.教师在教学中应该做好引导和组织工作，为学生的探究、发现搭建交流的平台，构建和谐的课堂氛围，鼓励学生积极探索，获得新知和运用知识的技能.通过问题激发学生思考，这是锻炼学生思维、导入概念的重要途径.

案例4三角形的角平分线和中线.

教学“三角形的角平分线和中线”时，传统教学一般是采用直接画一个三角形，在三角形中画出中线、角平分线的方式让学生认识三角形的中线和角平分线，接着进行试题训练，检测学生的掌握情况.这样的概念教学看起来非常自然，实则带有直接记忆和模仿的特点，学生的思维没有得到有效的锻炼，缺少了过程的体验和感受，难以真正理解三角形角平分线和中位线的概念.因此，教师可以通过问题的方式驱动学生思考，引导学生主动探究和获取知识，这样不仅能让学生收获有关的数学概念知识，还能锻炼学生的思维.因此，笔者教学时进行了如下的导入设计：

先在黑板上任意画出一个△ABC.

（1）能不能在BC边上找到一点D，连接AD后，AD将△ABC分成面积相等的两部分？

（2）点P是直线BC上的一个动点，连接AP，线段AP在什么时候长度最短？

（3）你能在BC边上找到一点E，使得∠BAE和∠CAE相等吗？

上述问题能引发学生进行如下思考：两个等高的三角形在什么情况下面积相等？在直线外一点到直线上各点的距离中，什么时候距离最短？怎样找到使两个角相等的点E？通过以上问题的探究，学生不难发现点D是线段BC的中点，AP⊥BC，AE平分∠BAC，从而自然地引出所要学习的概念.

游戏导入概念学习

数学游戏是调动学生学习兴趣的重要手段之一，可以使学生调动多种感官参与学习，发挥最大的学习潜能，提高学习效率.数学概念的学习一般较为抽象、复杂，如果教师能根据学习目标设计有趣的游戏，便可以营造轻松愉快的学习氛围，收到意想不到的学习效果.

案例5无理数.

无理数的定义是无限不循环小数，如果只是让学生记住这个定义，学生不仅很难理解，而且具体辨析某个数是否为无理数时也常常出错.所以笔者通过数学游戏的方式进行无理数概念教学的导入.

游戏准备：将一个圆形转盘分成10个相等的区域，分别写上0～9这10个数字.

游戏过程：让学生旋转转盘，并请学生将每个人转到的数字在小数点后面记录下来.随着转转盘学生的增多，所得到的数字的位数也越来越多，并得到了0.3982748…

师：如果我们一直转下去，会得到一个什么样的小数呢？

生1：会得到一个无限多位的小数.

师：这会是一个无限循环小数吗？

生2：不是无限循环小数.

师：为什么呢？

生2：因为转盘上有10个数字，每个人所转的数字不确定，所以一般来说数字不会重复循环.

师：是的，这个小数与我们前面所学的有限小数和无限循环小数不同，是一种新的小数.在数学上，我们把这一类数称为无理数.下面，我们就进入无理数的学习……

通过游戏体验，学生对无理数有了非常直接的体验，不再觉得无理数遥不可及，而是更加易于接受，也让数学概念的学习有了更加丰富的意义.

提升内驱力导入概念学习

学习的内驱力是学生能够保持长期学习的动力，那在概念学习中，如何才能激发学生学习的内驱力呢［2］？首先要有能够吸引学生的要素.只有学生感兴趣的话题才能让学生的注意力更加集中，并充满兴趣.教师在进行问题设计时，还要注意问题的难度，如果所提问题学生不需要过多的思考，那么很难激发学生的学习欲望，因此教师在教学时要设计可以驱动学生进行思考的问题，唤起学生的兴趣，让学生有明确的探究目标，从而进入新概念的学习.

案例6平面直角坐标系.

平面直角坐标系离学生的生活较远，因此教学时教师要拉近其与学生之间的距离，让学生更加直观地体会到平面直角坐标系的作用.笔者教学时进行了如下教学设计：

（1）数轴是什么？

（2）数轴上的点有什么含义？

（3）学校在车站西面100 m处，少年宫在车站的东面50 m处.请在数轴上标出学校、少年宫和车站的位置，并说一说这样标记的理由.

（4）车站的南面50 m处有一个公园，你能在数轴上标出公园的位置吗？

上述问题由易到难，第（1）（2）问是已经学过的内容，第（3）问比较简单，第（4）问则增加了难度，学生无法在数轴上标出相应位置.第（4）问引发学生思考，经过讨论，他们得出可再画一条与已知数轴垂直的数轴便可标出公园的位置，由此平面直角坐标系的概念呼之欲出.这样的问题在学生已有知识的基础上引发新的思考，既能培养学生思维的深刻性，又过渡自然，概念的导入也水到渠成［3］.

总之，数学概念的导入应遵循学生的认知规律，应在学生已有经验的基础上进行教学设计，应引导学生深入理解数学概念，以推动学生思维能力的提高.