激发合理猜想,成就数学学习的翅膀
2022-12-25卜英俊
卜英俊
江苏省常熟市海虞中学 215519
猜想在数学学习过程中是一种重要的探索手段,在数学发展史上很多伟大的定理都是通过猜想发现的,当然也有一些猜想被验证是不正确的.无论成功与失败,都表明猜想是学习数学的一种重要的能力.学生具备了猜想的能力,就为数学学习插上了想象的翅膀,学会了提出问题并解决问题,使自身的思维得到进一步的锻炼.
关于数学猜想的含义
数学猜想不同于想象,它是以数学知识为基础,在已有规律的基础上,通过数学方法进行推断或者推测.猜想的过程是运用数学知识进行分析和判断的过程,因此提出猜想本身就包含着创造性的劳动.正是因为有很多伟大的猜想,推动着数学理论不断发展,甚至在论证一些猜想的过程中还能发现其他的数学定理.因此培养学生的猜想能力,对于促进学生敢于质疑、敢于提出问题、敢于创新具有非常重要的意义.
如何培养学生的猜想能力
数学猜想能力的培养体现在课堂的每一个环节、每一个设计当中,教师只有深知教学活动与学生思维之间的关系,才能在活动中训练学生的思维,让课堂充满活力.
(一)动手实践,激发猜想兴趣
思维的锻炼与实践密切相关,学习过程中如果都是间接经验,学生不会有深刻的体会.而通过直接的动手操作,可以让学生在获得直接经验的过程中,激发猜想的兴趣.
案例1三角形中位线定理
师:同学们已经学习了三角形中位线的概念,那么三角形的中位线有哪些性质和特征呢?同学们不妨来自己动手画一画,看一看,想一想.
同学们应注意任何线与线的关系都有两种,一种为位置的关系,一种为数量之间的关系.同学们可以大胆地猜想一下.
生:我根据刚才画的几条中位线发现,三角形的中位线与三角形的第三边平行而且长度等于第三边的一半.
师:好的,同学们既然有了猜想,那我们要试着去论证一下这个猜想是否正确.大家可以试着动手做一下.大家做一个如图1的三角形,沿着三角形的中位线把△ADE剪下来,试着把△ADE和四边形BDEC拼接成一个平行四边形(如图2).

图1

图2

图3
师:看来同学们都拼接成功了,其实我们发现拼接的过程就相当于将DE延长,使E成为DF的中点,那么如何证明刚才你们的猜想呢?
生:通过三角形相似原理,BD∥CF,DF∥BC,也就证明了四边形BDFC是平行四边形,那么BC和DF相等,而E成为DF的中点,因此DE是BC的一半.
本例中教师并没有将定理直接告知学生,而是引导学生通过自己的作图和观察进行猜想,继而又通过剪拼发现了证明猜想的办法,这一系列的思维活动通过发现问题到证明问题,最终使学生获得成功的喜悦,激发了探究的兴趣.学生有了兴趣的驱使,学习就变得轻松愉快,自然愿意投入更多的时间和精力,愿意发挥自己的主观能动性去积极的探索和学习,让学习真正成为一种自觉.
教学中教师要积极创设活动,让学生主动参与,动手实践,大胆猜想,运用自己所学的知识大胆设疑、充分证明,激发自身学习的积极主动性.
(二)掌握方法,培养猜想能力
数学猜想是在已有数学知识的基础上,采用数学方法进行的推理,因此掌握数学方法是猜想需要的前提.猜想过程中普遍需要用到归纳和类比转化的思想,在教学中教师要不断培养学生归纳和类比的数学推理方法.
1.学会归纳方法
归纳是学生提高学习效果的重要方法.简而言之,归纳是由零散到整体的总结,是由特殊的例子推而广之成为普遍的定理.
案例2凸多面体中面、棱和顶点的关系
探究这其中的关系较难,凸多面体也无法穷尽,所以可以采用举例研究特殊图形来找到规律.教师引导学生通过列表格进行分类整理(如表1),在整理的过程中发现面、顶点和棱虽然增长的数量不一致,但是都有着同样的增加或者减少的趋势.再仔细研究学生就会发现面与顶点的和等于棱的数量加上2.

表1
本案例是典型地采用了归纳推理的方法.研究一种较难的数学定理或者猜想时,不要妄想一步登天,可以从最简单的部分着手,为了更加清楚直观,可以尽量采用列表、举例的方法,多举一些简单的例子进行观察,从变化当中发现不变的规律,自然可以发现其中的定理.在教学中教师要逐步引导学生通过特殊到一般的推理,有效简化推理的过程,论证猜想.
2.学会类比思想
类比思想是根据同类事物进行猜想和推理,在数学问题的解决过程中,类比思想应用非常广泛,很多重要的数学定理的论证就是通过类比思想完成的.
案例3多边形内切圆半径
问题1:如图4,已知三角形ABC的周长为l,三角形内部有一个内切圆O,其半径为r,以O为顶点划分成三个三角形.经过证明可知三角形ABC的面积等于三角形周长乘以内切圆半径的一半.由此得出猜想1:若四边形ABCD有一个面积为s的内切圆,四边形各边长分别为a,b,c,d,求推导出内切圆的半径.

图4
问题2:如图5,圆O为四边形ABCD的内切圆,OA,OB,OC,OD 将四边形ABCD 分割成四个三角形,△OCD,△OCB,△ODA,△OAB的高都是圆的半径,因此r=.据此可得出猜想2:若一个n边形存在内切圆,且已知圆的面积为s,边长分别为a,b,c,d…n,根据以上的猜想可以得到这个内切圆的半径为r=
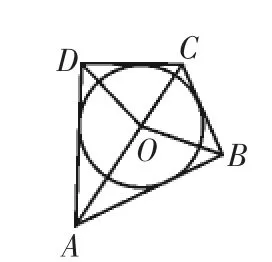
图5
本题通过典型的类比思想,先从三角形推理到四边形,进而再推广到n边形,使一个复杂的问题得以推理论证.类比思想就是对相似的性质、过程或者结构等进行联想和推理,教师在进行定理的讲解、习题的练习时都可以潜移默化地渗透这种思想,使学生利用知识之间的联系和类比,进行合理的猜想和推理.
加强变式练习,提高猜想能力
变式训练是有效拓展学生思维的方法,教师只有进行大胆的思维训练,才能让学生大胆质疑和猜想,提高猜想能力.
案例4
原题:如图6,以△ABC的两条边AB和AC为边,向外作正三角形ABD和ACE.请证明BE=DC.
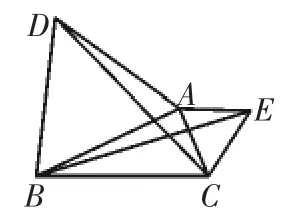
图6
本题是一道并不困难的证明题,如果只是讲解这道题,并没有很好地发挥它的作用,可以改变已知条件,也可以改变结论,还可以将图形与函数相结合,让这道题真正发挥出它的潜在价值——一题多变.
变式1:在已知条件不变的情况下,增加求答问题.
以△ABC的两条边AB和AC为边,向外作正三角形ABD和正三角形ACE.(1)证明BE=DC.(2)猜想直线CD与直线BE的夹角有什么特征?
变式2:增加新的结论,逆向推导已知条件.
如图7,以△ABC的三条边AB,AC,BC为边,在BC边的一侧作等边三角形BCF、等边三角形ACE和等边三角形ABD,请证明四边形DAEF是平行四边形.
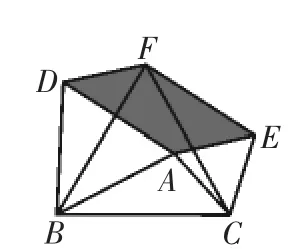
图7
猜想:当△ABC在什么情况下,四边形DAEF是矩形?当△ABC在什么情况下,四边形DAEF是菱形?当△ABC在什么情况下,四边形DAEF不存在.
通过改变已知条件,将试题变成一道几何综合题,增加了题目的难度,也需要学生运用综合思维能力以及分析和逻辑推理能力,在变式练习的过程中,学生的猜想能力得到了提高.猜想是思维的综合运用,在教学中教师需要鼓励学生大胆思考,对学生的想法要多鼓励和表扬,不能直接否定,可以通过引导分析,让学生逐渐找到思路.只有在不断的训练过程中,学生的猜想能力才能得到提高.
总之,猜想可以使学生锻炼思维,学会类比转化思想,进行更加综合的思考,让知识更加深刻;猜想还能增加学生的自信,培养学生的创新意识.猜想是兴趣使然,反过来又能激发学生的学习兴趣,所以教师要充分利用好猜想,让它为学生的学习插上飞翔的翅膀,让学生飞得更高、更远.
