流固耦合效应对进水塔结构动力响应特征影响研究
2022-12-24白文龙
白文龙
(深圳市深水水务咨询有限公司,广东 深圳 518000)
水工建筑安全稳定性一方面取决于静荷载下结构应力、位移特征,同时不可忽视地震动荷载下结构应力、位移响应特征[1-2],此对水工结构抗震设计具有重要启发意义。进水塔乃是水电站等水利枢纽工程中重要组成部分,其运营安全与塔体自身结构特征参数密切相关[3-4],也与静、动力荷载状态有关,而其中动荷载状态包括有不同类型的输入地震动。李伟[5]、李锋等[6]为研究进水塔结构静、动力特征,借助Abaqus、ANSYS等仿真平台,开展了进水塔自身锚固参数影响下的静、动力响应特征分析,从结构应力、位移变化评价进水塔结构设计方案。也有赵杰等[7]、刘浩[8]从地震动非线性输入方面入手,探讨振型分解法、反应谱叠加法以及拟静力法等不同动力响应特征计算方法下,进水塔等水工结构动力响应特征差异。流固耦合是进水塔结构动力响应分析不可回避的问题,如何有效模拟流固耦合作用,对系统性评价进水塔结构动力响应特征有重要意义,程琦[9]、王忠等[10]提出ALE网格、有限元网格、无网格等不同类型的解决方案,并在实际工程中进行验证,探讨流固耦合非线性作用下水工建筑动力响应演化特征。本文为探讨沧江水利枢纽进水塔结构动力响应特征,引入四种不同类型地震波输入方案,探讨地震波类型对流固耦合场中进水塔结构动力响应特征影响,为水工抗震设计提供基础参考。
1 研究方法
1.1 工程概况
广佛地区水资源丰富,地表流经河流包括有珠江、沧江等干流,其中沧江乃是佛山地区重要水位调节、蓄洪排涝枢纽,控制流域面积超过2500km2,对广佛城市一体化经济建设具有重要水利优势。每年夏季乃是广佛地区台风汛期防洪压力最大时,目前已有的沧江水利枢纽包括有电排站、泄洪闸以及引水工程等,各水工设施所在河段分散性较大,对区域内综合水资源的利用处于较为不利状态,特别是电排站原设计最大排涝量可达300m3/s,但目前受限于泥沙淤积、河床水位抬高、堤防防渗不足影响,导致电排站在台风汛期常出现进水口泥沙堵塞、排涝量过小的局面,此对城区防洪排涝带来较大不利影响。综合现有水利设施运营考虑,沧江管理部门计划在佛山高明区沧江下游段Z6+232段新建一综合小型水利枢纽,该枢纽工程具有防洪排涝、引供水以及通航的水利作用,工程内容包括有泄洪闸、泄洪洞、溢洪道、引水渠道及其附属进水塔等水工建筑。按照经济节俭的建设原则,部分水工建筑乃是在原有水工设施的基础上进行改进提升,如泄洪洞借助原有该位置的引水隧洞进行改扩建,设计最大泄流量可达555m3/s。该新建枢纽重点工程为溢洪道设施,其规划设计平面布置如图1所示,具有引渠段、泄槽以及消能段,泄槽段坡度为0.25,重建后溢洪道轴长为82m,配置有多层次多类型消能构件,比如宽尾墩、挑流鼻坎以及掺气坎等,设计最大消能率可达46.5%,该溢洪道与上游泄洪洞进水塔乃是主要的泄流建筑。进水塔高程为86m,该进水塔是水利枢纽规划的新型泄流设施,不仅具有引供水通道作用,同时具备泄流传导作用,其立面与截面几何示意如图2所示。进水塔内外水高程一致,截面高a、宽b分别为14.5m、13.5m,内部塔体截面c、d分别为6.8m、4.5m。进水塔投入运营后,动水压力冲击荷载自振影响下,塔体结构势必具有一定振型发展,对塔体内部水流进入溢洪道具有加大势能的作用。
1.2 动力响应模型
相比一般水工建筑动力响应特征分析,进水塔结构的地震动响应分析在于考虑水体存在影响,根据水工结构附加质量法,引入Westergard附加质量公式[11]:
(1)
式中,mw(h)—附加水体质量,g;ψm(h)—附加水体质量动水压力分布系数;ρw、ηw—水体标准密度,g/cm2;水体粘滞系数;A、H0—固体场触水面积,m2;水位,m;a—水体运动系数。
结合水工结构动力控制方程N-β,获得进水塔结构动力响应方程积分式:
(2)

考虑溢洪道泄洪洞与进水塔结构为步调一致性运营,因而动力响应方程中动力阻尼系数按照Rayleigh阻尼计算,如下式:
C=αM+βK
(3)
(4)
式中,ϖ1、ϖ2—第1、2阶数自振频率,Hz;ς—阻尼系数;α、β—Rayleigh动力系数。
不仅如此,考虑水体质量自身运动特性,引入水体N-S方程,如下式[12]:

(5)

进而,联系前述式(1)(2)(5),获得了进水塔结构流固耦合下运动方程,此也为本文开展流固耦合下进水塔结构动力响应计算的理论依据。
图3为采用ADINA有限元平台建立起进水塔内外塔体的计算模型。该模型中设计无水头压差,高程均为90m,塔内流体长度按照泄洪洞高度3倍取值,设定为43.5m,全模型中均采用四边形微单元作为分析模块,共获得计算网格单元326844个,节点数265284个。在进水塔模型的底部设置为无运动、无透水边界条件,所有水体模型表面均为自由面,按照Free-Surface边界设置水体,水体与塔体交界面上设置为流固耦合边界,ADINA可根据水体与塔体结构的主导作用识别网格单元。根据沧江水利枢纽规划,进水塔结构材料为C30混凝土,因而其静、动模量参数均按照该类型混凝土取值。
进水塔结构地震动力响应特征不仅与自身结构特征有关,与所输入地震波类型也密切相关,地震波类型的随机性,会导致水工结构动力响应特征出现显著差异性。为此,本文选取3种天然地震波类型与一种人工合成地震波进行动力响应计算,分别为EI Centro波、Taft波、广州波以及人工合成波,此四种类型地震波加速度时程特征如图4所示,前20s时程曲线中峰值加速度均为0.25g。基于不同类型地震波输入下,探讨不考虑水体质量与流固耦合作用下进水塔结构动力响应特征。

图1 溢洪道几何设计剖面、平面图
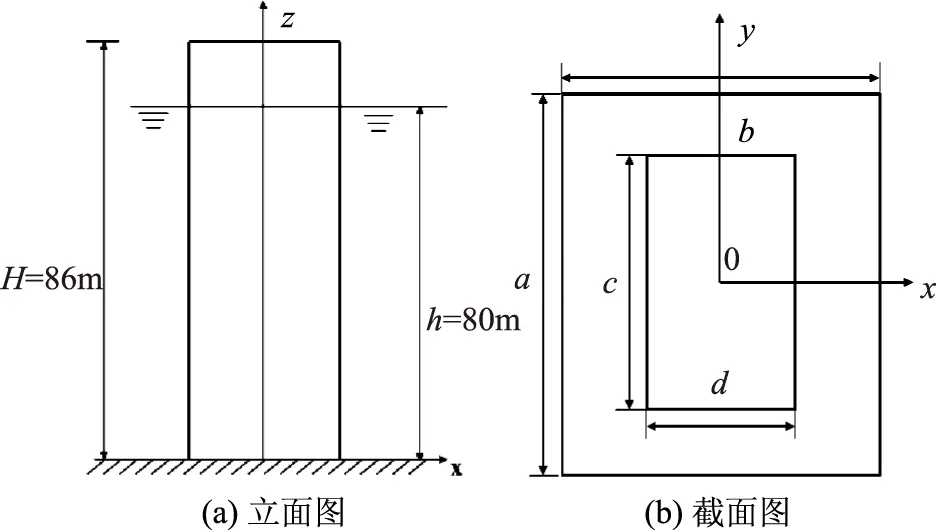
图2 进水塔几何示意
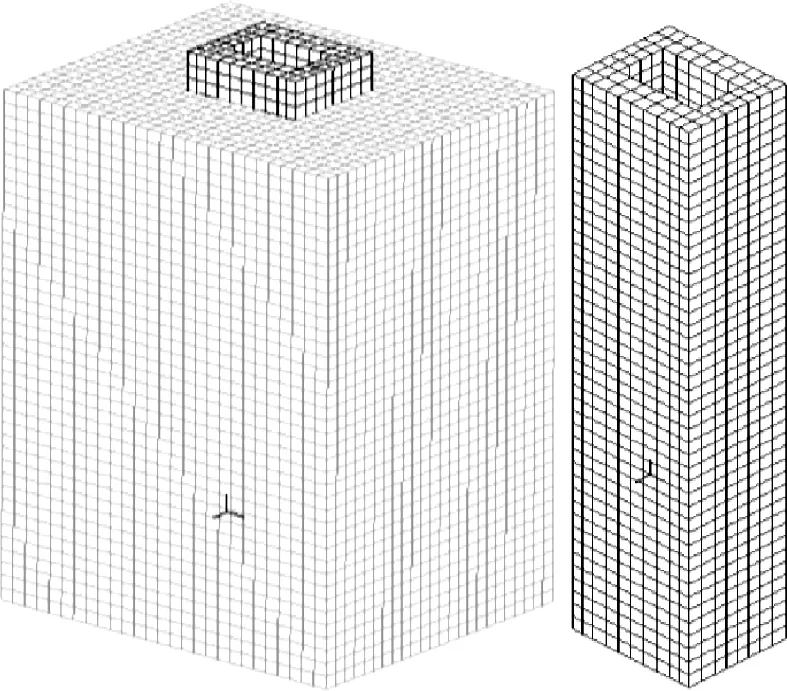
图3 进水塔体结构计算模型

图4 加速度时程特征
2 进水塔结构自振特性
基于进水塔结构自振特性计算,获得了塔体在无水工况及流固耦合下各阶自振特征,如图5所示。分析图中自振特征参数可知,随阶数增大,自振频率均提高,在流固耦合计算工况中,10个阶数中自振频率平均增幅为11.6%,而在无水工况下平均增幅为15.1%,即流固耦合下塔体结构自振频率受计算阶数影响敏感度弱于无水工况。相比之下,流固耦合工况中的塔体结构自振频率分布为3.15~8.38Hz,而无水工况下自振频率较前者提高了61.7%~115%,分布在5.1~18Hz。分析表明,塔体水流的存在,会增大塔体结构自身质量,导致自振作用下动力阻尼系数增大,使之自振频率故而低于无水工况[9,13]。

图5 各阶自振频率变化特征
进一步对前10阶数下塔体结构振型特征进行分析,如图6所示。从图中可看出,在第1~3阶数时,塔体结构以横向振型为主,而在第4~6阶数时,塔体结构具备有竖向扭动振型,当计算阶数为7~10次时,塔体振型以具有横、竖向组合式振型特征。由此可知,自振作用下,塔体结构为横向-竖向-横、竖向组合式振型演变特征。

图6 塔体结构振型特征
3 进水塔结构地震动响应特征
3.1 位移响应特征
基于四种不同类型地震波输入,并设定塔体中水位高度分别由0、15、30、45、60、75、90m梯次组成,计算获得流固耦合效应与无附加水体质量下塔体结构位移响应特征,如图7所示。

图7 塔体结构位移响应特征
由图中位移特征可知,当不考虑附加水体质量时,同一种类型地震波在水位0~60m下,其位移响应特征均为一致,而水位超过75m后,位移响应特征才具有一定增幅,即不考虑流固耦合效应下,位移响应特征与塔中水位呈“不变-递增”的两阶段特征。分析表明,不考虑附加水体质量,并不意味着塔中结构位移响应特征与水位毫无关联性,而是当水位超过塔中水位限值的80%后,其位移响应具有递增效应。从具体类型地震波的变化来看,广州地震波在水位75m后变幅最大,3方案间平均增幅可达35.5%,而人工合成地震波下位移响应值的变幅最小,仅有10.7%增幅,而EI Centro地震波、Taft地震波下的位移响应特征值在水位75~90m方案间平均增幅较为接近,为20%左右。除人工合成地震波外,其他3种天然地震波在水位低于75m下,位移响应特征值基本接近,稳定在11mm左右,而人工合成地震波在该水位方案下位移值低于前三者地震波,仅有5.28mm。综上可知,当不考虑附加水体质量时,水位对塔体结构位移响应特征影响具有高界限性,而该界限为75m;同时,自然地震波对塔体结构地震作用强于人工合成地震波,在高界限性影响阶段,前者类型地震波对位移特征影响变幅也高于人工合成地震波[7]。
当考虑流固耦合效应时,位移响应特征与塔中水位关系前者如图7(a)所示中有较大差异性,当水位增加,即塔中水体质量增大,进水塔结构整体质量放大系数加大,此时不论是何种类型地震波输入,结构位移响应值均减小。塔中水位从0m增大至80m的过程中,塔体结构位移响应值降幅最大属EI Centro地震波与Taft地震波,两者降幅分别达75.8%、74.7%,当塔中水位每增大15m,塔体结构位移响应值平均降幅分别为20.8%、19.9%,在水位限值90m时,两类型地震波下塔体位移响应值分别达3.1、3.3mm。相比之下,在各水位方案中,广州地震波、人工合成地震波对塔体结构位移响应值影响幅度较弱,特别是广州地震波输入方案,在塔中水位45m后即处于位移响应值恒定状态,而人工合成地震波输入时,各方案中位移响应值均处于缓降状态,平均降幅仅为7.5%。分析表明,流固耦合作用下,水体质量有助于削弱塔体结构位移响应,但以EI Centro地震波与Taft地震波对进水塔结构位移响应最为敏感,而广州地震波作用下塔体结构位移响应水平较高,但受塔中水位影响敏感较弱。
3.2 应力响应特征
从进水塔结构动力响应特征中不仅可获得位移响应特征,亦可获得应力响应特征变化,本文从应力响应时程特征曲线中提取获得不同水位下塔体结构第一主应力峰值变化特征,如图8所示。
由图中应力响应特征可知,当不考虑水体质量时,无论输入地震波为何种类型,其应力响应峰值均随水位为递增变化。如在广州地震波输入方案,当塔中水位为15m时,其第一主应力响应峰值为2445.95kPa,而塔中水位为45、75、90m时主应力响应峰值分别提高了16.6%、34.1%、44.8%,从水位变幅层次来看,广州地震波输入方案下主应力响应峰值的平均增幅达7.6%。在EI Centro地震波、Taft地震波以及人工合成地震波输入方案中,主应力响应峰值分别具有增幅15.8%、10.6%、13.3%,即不考虑水体质量工况下,以EI Centro类型地震波受塔中水位影响敏感度最高。
当附加水体质量后,整体上主应力峰值均低于前者工况,EI Centro地震波输入方案下,两者工况在各水位下应力响应峰值差幅分布为4.3%~86.9%,尤以人工合成地震波在考虑与不考虑水体质量工况对比下应力响应差幅最显著,达22.2%~90.5%。当进水塔结构处于流固耦合场时,塔中水位增大,其主应力响应峰值呈一致性递减变化,此影响变化特征与不考虑水体质量下呈鲜明差异[3,14]。EI Centro地震波输入方案中主应力响应峰值在水位15m时为701.3kPa,而在水位90m时为264.5kPa,各水位方案间主应力响应峰值平均降幅为22.4%;而Taft地震波在水位15、90m下分别为742.3、156.2kPa,各方案间随水位15m具有平均降幅17.8%;广州地震波、人工合成地震波下平均降幅分别为2.4%、16.3%。对比来看,以EI Centro地震波受水位影响敏感最大。进一步对比各类型地震波输入方案下的主应力响应峰值,以广州地震波输入下最大,该方案下主应力峰值分布为1346.98~1554.2kPa,而人工合成地震波输入下应力响应峰值水平最低,仅分布为71.1~262.9kPa。由此可知,人工合成地震波在考虑水体质量的前提下,塔体结构主应力响应峰值水平较低,而天然地震波中以广州波下响应峰值水平最大,但其受水位影响较弱。

图8 塔体结构第一主应力响应特征
4 结语
(1)流固耦合场中自振频率低于无水工况;自振作用下塔体结构振型由横向-竖向-横、竖向组合式振型演变。
(2)当不考虑水体质量时,位移响应值随塔中水位呈“不变-递增”特征;自然地震波下塔体位移响应强于人工合成地震波。
(3)考虑流固耦合场时,位移响应值随塔中水位为递减变化,而降幅最大属EI Centro与Taft地震波,广州地震波输入下位移响应水平最大,人工合成地震波输入下位移响应最低。
(4)不考虑水体质量下,以EI Centro地震波输入下主应力响应峰值受水位影响最大;人工合成地震波输入下有、无考虑水体质量下应力响应峰值差幅最大。
