General design principle of artillery for firing accuracy

Linfang Qian,Guangsong Chen,Minghao Tong,Jinsong Tang

School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing,210094,China

Keywords:Firing accuracy Projectile-artillery coupling Rotating band conformal Sensitivity analysis Error control

ABSTRACT In this paper,based on the topological description method,the kinematic and dynamic equations of the projectile flight and projectile-artillery coupling system during the whole process of firing are constructed.The factors that can affect the projectile burst points,namely the state parameters of the projectile on the muzzle and state parameters of the barrel muzzle,as well as the factors that affect the barrel muzzle state parameters,are analyzed.On this basis,the design principle of artillery firing accuracy is proposed.The error analysis and the corresponding inverse problem,the extraction method of key parameters affecting artillery implicated motion,the conformal and control method of rotating band are analyzed and presented.Finally,the presented method is verified through a vehicle mounted howitzer case,and the muzzle state parameter interval is obtained meeting the given firing accuracy.In addition,the sensitivity analysis of artillery parameters shows that the less the correlation between the parameters and the barrel,the less the influence on the projectile implicated motion.The analysis of the coupling effect between rifling and the rotating band shows that the uniform rifling is the optimal form for the conformal of the rotating band during firing.

1.Introduction

Artillery firing accuracy refers to the statistical value of the deviation between a group of burst projectile points and the target point.It is not only one of the core indicators of artillery but also a difficulty issue in artillery industry research[1-3].It is becoming and more important to improve the firing accuracy of artilleries on the modern battlefield,especially for the demands of covering targets by first group shooting,hitting the target on the first shoot,and destroying targets on hitting.Meanwhile,as the primary combat equipment,the artilleries’high-efficient strike capability with low cost is not only the requirement of the industry promotion but also an important direction for competing development[4].Artillery firing accuracy design is to analyze the key factors that can affect the firing accuracy,and to improve the firing stability and reduce the disturbance of the projectile by modifying these factors during the overall design stage.However,since the firing accuracy is caused by the superposition of random factors of all parts in the artillery weapon system during the whole firing process,there are numerous and complex factors affecting the firing accuracy,the error distribution and transmission law of key factors are difficult to control,and the lack of methods to obtain the key parameters during the firing process makes the firing accuracy a major technical problem that has been perplexing the model development of artillery industry[4,14].

Artillery firing accuracy is closely related to the development of artillery dynamics.From the first international ballistic conference held in the United States in 1974 to the 31st international ballistic conference held in India in 2019,the motion of projectiles in bore and artillery dynamics are two important themes in every conference[5,6].For a long time,many researchers have done long-term researches on the load environment,projectile-barrel coupling,projectile motion property,and so on,and have achieved fruitful results.Newill[7]et al.developed the artillery system dynamics analysis software and verified the model through tests.Ray[8]studied the influence of equipment manufacturing accuracy on firing accuracy and projectile dispersion in detail.Chen[9]studied the influence law of barrel bending on nutation motion of projectiles in bore,and gave specific calculation formulation.Tabiei[10]et al.studied the coupling motion of the projectile and flexible barrel in the bore by using Lagrange and ALE methods.Han[11]systematically analyzed the factors affecting the burst point distribution of projectile by establishing external ballistic equations with different complexity and gave the physical explanation of the influence of muzzle state parameters on firing accuracy.Guo[12]established a model of long-range artillery which can analyze the relationship between the firing accuracy and the state parameters of the projectile muzzle,and deeply studied the influencing factors and the test technology.Rui[13]analyzed the firing dispersion based on the maximum entropy method and obtained that the distribution of projectile burst point is a quasi-normal distribution with skewness,which has very important practical value for the application of artillery firing accuracy.Wang[14]discussed the factors affecting the firing dispersion of artillery and summarized the technical means taken to develop artillery weapon models and improve the firing dispersion.Feng[15]analyzed the sensitivity of parameters affecting the firing dispersion based on the Latin hypercube sample method and range analysis method,and explored the influence property of structural parameters on firing density.Wang et al.[16]proposed a random parameter interval analysis method and gave the final optimal parameter scheme for given dispersion requirements.Based on continuum mechanics and modern probability theory,Qian et al.[17]research the motion characteristics of projectile during the internal and external ballistics,and the corresponding uncertain of the state of projectile are also discussed.The PRODAS ballistic software was used by Dursun to model the projectile-gun system and identify the effects of the projectile muzzle velocity,forward and rear bourrelet diameter,manufacturing tolerance,gun support stiffness and recoil stiffness on the projectile dispersion[18].Leonhardt et al.[19]measured five different experimentally bore center lines and analyzes the effect centerline nonlinearity on projectile exit conditions by using Abaqus/Explicit.Wang et al.[20]proposed a nonintrusive interval uncertainty propagation approach for the response bounds evaluation of artillery multibody dynamics model created in ADAMS/Solver,and the interval response of the artillery is obtained.Le et al.[21]investigated the individual and combined effects of disturbance factors including trust misalignment,the offset of the center of gravity and misalignment of the principal axes of inertia on falling point distribution of a type of unguided rocket.Alosaimi[22]presented the model-based system engineering methodology to predict modular artillery charge system performance,and identified the sources of error that can determine the performance of MACS in both launch phase and in-flight phase of the projectile.The research derived the errors in the launch phase and investigated their implication to the overall performance(in form of dispersion and accuracy).Khalil[23]assessed the tabulated FT modeling and production accuracy,in terms of the input meteorological data,the elevation and azimuth angles round-off,and Earth’s rotation approximation.It was validated in a 155M107 projectile.Ding et al.[24]developed a test method that combines an inertial measurement system with a high-speed photogrammetric system to measure the muzzle response,and obtained the muzzle response characteristics of small unmanned ground vehicles with small arms(SUGVsSA)during shooting.Koç[25]applied the adaptive neural fuzzy model to estimate the vibrations at the tip of an antiaircraft barrel considering different ammunition.Kasahara et al.[26]presented a seamless calculation of the acceleration phase in the tube and the full separation process using 3-D computational fluid dynamics coupled with rigid body dynamics to investigate the shockwave interactions around a railgun-launched projectile.Other researches about fire accuracy,muzzle disturbance and projectileartillery coupling dynamics in recent years can be found in Refs.[27-29].These researches have systematically formed the theory of artillery firing accuracy analysis.However,the related inverse problem,namely the design principle of artillery firing accuracy,needs to be further investigate.

In general,for the uncontrolled projectile launched by artillery,the factors that affect the firing accuracy include meteorology and artillery firing.Among them,the meteorological conditions focus on the interaction between air and projectile,which is an important part of exterior ballistics and projectile design;Artillery firing focuses on how to give the initial conditions for the projectile to fly and the effect on the shape of the projectile,which needs to be considered in the process of artillery design,and is also the focus of this paper.Therefore,in order to more clearly show the effect of artillery firing on firing accuracy,meteorological conditions are regarded as a stable process,that is,ideal meteorological conditions,without considering the effect of changes in meteorological conditions on projectile flight,so as to obtain the effect of various factors of artillery on firing accuracy in the process of artillery firing through theoretical modeling and analysis.

In this paper,based on the topological description method,the kinematic and dynamic equations of the projectile flight and projectile-artillery coupling system during the whole process of firing are constructed.The factors that can affect the projectile burst points,namely the state parameters of the projectile on the muzzle and state parameters of the barrel muzzle,as well as the factors that affect the barrel muzzle state parameters,are analyzed.On this basis,the design principle of the artillery firing accuracy is proposed,including the transmission and reverse calculation of the parameter errors,the extraction of the key parameters affecting the barrel traction motion,and the rotating band conformal,etc.Finally,the case study and verification are carried out through a vehicle-mounted howitzer.

2.Coordinate system establishment

It is assumed that the target coordinates have been determined,the meteorological conditions are stable,the firing data is accurate,and the start time of projectile transmission is the same as system movement,recorded as t=t0=0,the time when the projectile exit of shot is recorded as t=tG,and the time when the projectile reaches the burst point,that is,the time when the flight ends,is recorded as t=tC.

The sketch and the coordinate system of a howitzer artillery is shown in Fig.1.A,B,C and Dare respectively used to represent the four generalized parts of the artillery,that is the chassis,upper frame,cradle,and barrel.The projectile is represented by Q,and the rotating band is represented by F.In order to describe the motion of artillery,it is necessary to establish the relevant coordinate system.(1)Inertial coordinate system oG-xG1xG2xG3is denoted as iG,and The unit base vector of the coordinate axis isiGej(j=1，2，3).The coordinate origin oGis located on the ground and coincides with the midpoint of the connecting line between the center of the left and right spade.(2)The coordinate systems of chassis,upper frame,cradle,and barrel are respectively recorded asA，B，C，D).The origin oAof iAis located at the midpoint of the front axle axis of the chassis,and the base vector of the coordinate system is represented byiAej(j=1，2，3).The origin oBof iBis located in the lower plane of the upper frame and coincides with the center of the inner race,and the unit base vector of the coordinate axis is represented byiBej(j=1，2，3).The origin oCof iCis located at the midpoint of the connecting line of the trunnion on the cradle,and the unit basis vector of the coordinate system is represented byiCej(j=1，2，3).The origin oDof iDis located at the intersection of the barrel axis and the front-end face of the breech,and the unit basis vector of the coordinate system is represented byiDej(j=1，2，3).(3)The projectile coordinate system iQ,that is oQ-xQ1xQ2xQ3.The coordinate origin oQis located on the geometric center of the projectile,and the unit basis vector of the coordinate system is represented byiQej(j=1，2，3),as shown in Fig.2.

The transformation relationship between different coordinate systems can be shown in Fig.3.For example,the transformation relationship between the iDand iGcan be directly given as iD=LiD·LiC·LiB·LiA·iG.ivis the velocity coordinate system and Lδis the transformation tensor between the velocity coordinate system ivand the iQ.The detailed of the definition of coordinate system the transformation relative of the coordinate system is given in Ref.[17].

3.Flight motion of projectile

3.1.Exterior ballistic motion equation

Fig.4 shows the state of the projectile in the air.According to the external ballistic equation of the rigid body with 6◦of freedom,the state of the projectile in the air at any time t can be described by the following 12 state variables:

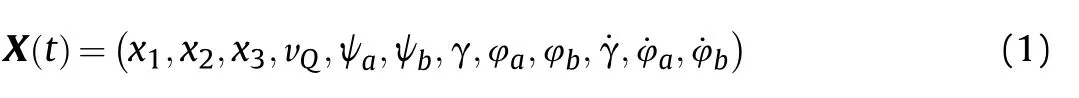
Fig.1.Coordinate system.

Fig.2.Projectile coordinate system iQ.

Fig.3.Transformation relationship between coordinate systems.

where,x=xjigejis the position vector of the projectile geometric center oQrelative to og;.x=.xjigej=vQive1is the velocity of the projectile geometric center oQrelative to the coordinate system ig,vQ=‖‖is the modulus of the projectile geometric center velocity,ψaand ψbis the velocity deflection angle,andive1=cos ψbcos ψaige1is the direction of the velocity unit vector;φaand φbare the swing angle of projectile axis;.φaand.φbare the angular velocity of projectile axis;γ and.γ are the rolling angle and angular velocity of the projectile axis.

In addition,there is a pair of dependent state variables,namely the angle between the projectile axis and the velocity axis,called the attack angles δ1and δ2.The attack angles δ1and δ2have the following relationship with the deflection angles ψaand ψb,and the swing angles φaand φb

The angular velocity of the projectile relative to the coordinate system igis given by Ref.[17]

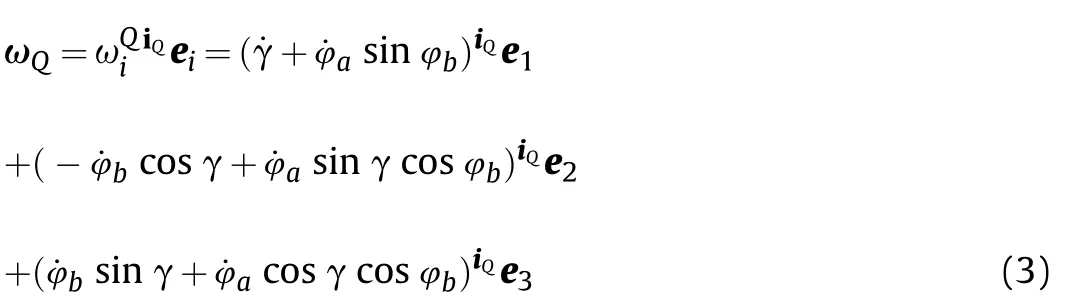
For any point on the projectile OQ,the position vectorof the point in the coordinate system iQ,and the position,velocity and acceleration vector in the coordinate system igare respectively as

Fig.4.The degrees of freedom of projectile.

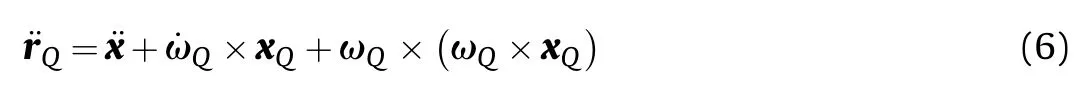
Once the projectile flies in the air at a certain Mach number and attack angle,a certain pressure will be generated on the surface of the projectile,formed aerodynamic force and aerodynamic torque which can be simplified to the geometric center oQof the projectile.Aerodynamic force can be decomposed into drag FD,lift FLand Magnus force FM.Aerodynamic moment can be decomposed into static moment Mz,equatorial damping moment Mzz,polar damping moment Mxz,Magnus moment My,unsteady damping moment M.α,etc.The detail expression of these forces and moments can be found in Ref.[11].

Based on the virtual power principle,the differential equation of projectile can be obtained as

where

in which

where,ΩQis the volume domain of the projectile,mQis the mass of the projectile,xQGis the eccentricity,IQis the moment of inertia,and~xQis the second-order cross product tensor of vector xQ.

3.2.Muzzle initial condition

The instant when the rear end-face of the rotating band exit the muzzle is defined as the moment t=tGas shown in Fig.5.At this time,the initial conditions for the projectile exit the muzzle are as follows:

where

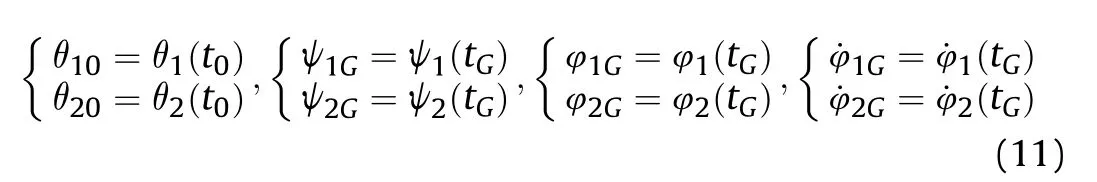
When t=tG,the motion state of the projectile at the muzzle is

and attack angle and velocity of attack angle are

The angle of the barrel at time t=tGis

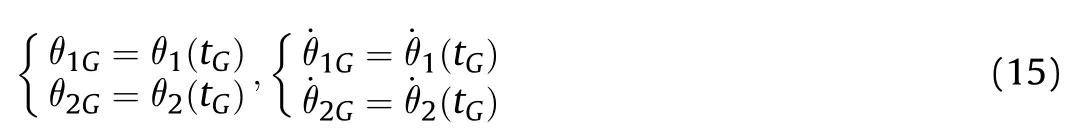
By solving Eq.(7)with Eq.(12)and Eq.(13),the general expression of the following solution can be obtained:

where,F is the force and moment given by Eq.(8).

If Eq.(16)takes value at time t=tC,the position vector of burst point can also be obtained

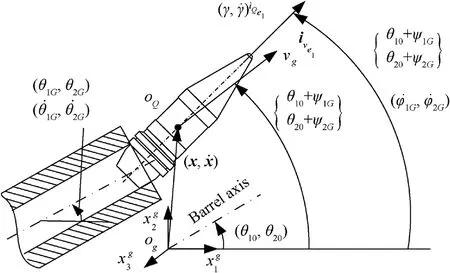
Fig.5.Muzzle state variables of projectile.

3.3.Factors affecting the position of projectile burst point

It can be seen from Eq.(18)that the position coordinate x of the projectile is related to the initial condition XGof the muzzle and the aerodynamic load F.Assuming that the plastic deformation and conformal performance of the projectile,especially the rotating band is consistent during in bore,then x is only related to XG.The factors in XGthat have an important impact on x are discussed below:

(1)By observing the specific composition of XG,we can find that xG=x(tG)is very small compared with the position coordinate xC=x(tC)of projectile burst point,so its influence can be ignored.

(2)vghas an important influence on xC,but from the perspective of artillery overall design,vgis determined by charge structure and interior ballistic design.In the overall design process of considering firing accuracy,the effect of charge structure on vgerror or burst point dispersion needs to be analyzed separately.For the artillery structure design,the effect of charge structure on vgerror and burst point dispersion can be considered as a fixed part.So,it may not be considered in this paper.The detailed of the vgand other muzzle state parameters error to the burst point dispersion can be found in Refs.[30,31].

(4)In this way,from the perspective of the overall design of the artillery,the muzzle factors that have an important effect on xCare only:

Obviously,it can be seen that the factors that have an important impact on xCin XGare the amount of angular motion.According to the synthesis principle of angular motion,the angular velocity of the projectile is the sum of the implicated angular velocity of the barrel and the angular velocity of the projectile relative to the barrel.Therefore,ψ1Gand ψ2Gare related to the muzzle transverse velocity of the barrel,and φ1G，φ2G，.φ1G，.φ2Gare related to the muzzle transverse angular motion of the barrel.

Therefore,the overall design task of artillery firing accuracy is.

(1)Control the muzzle transverse angle motion and transverse velocity of the barrel;

(2)Control the coupling between the projectile and the barrel,so as to control the relative angular motion of the projectile;

(3)Control the plastic deformation and conformal consistency of rotating band to ensure the consistency of aerodynamic force.

Since vghas an important influence on xC,the influence of vgshould be considered in Eq.(18)in the subsequent discussion,i.e.

4.Projectile-artillery coupling motion

4.1.Basic agreement

Let rI,and(I=A，B，C，D)are the position,velocity and acceleration vector of the local coordinate system origin oIon the vehicle-mounted howitzer component I relative to the inertial coordinate system origin oG;ωIand.ωIare the absolute angular velocity and angular acceleration of component I respectively;Recordandare respectively the position,velocity and acceleration vector of the origin oJof the coordinate system on part J relative to the origin oIof the coordinate system on part I;ωIJ.is the angular velocity and angular acceleration of component J relative to component I;Record

4.2.Projectile-artillery coupling motion equation

Considering components B and components A,the following relationship exists:

Then,the position,velocity and acceleration vector of any point xBon the component B can be expressed as

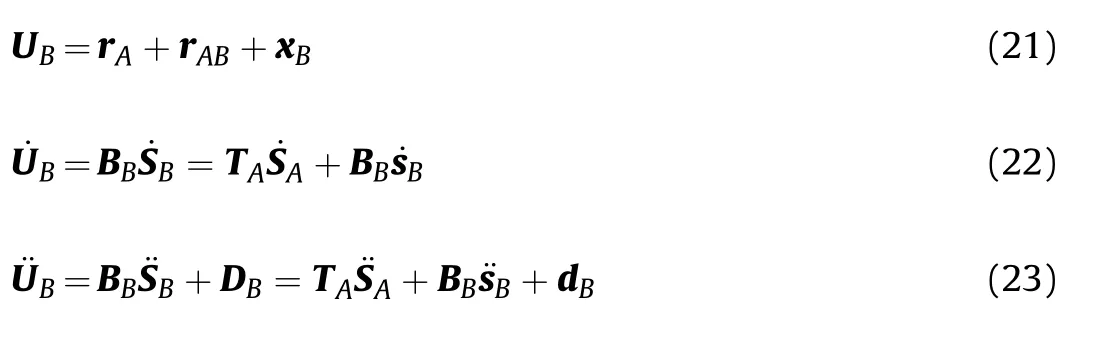
Similarly,the displacement,velocity and acceleration vector UK,,of any point xKon component K(K=C，D，Q，F),and the corresponding BK,TKand dKcan be obtained.

where wFandare respectively used to represent the elasticplastic deformation and deformation velocity of the rotating band.

According to the system topology described in Fig.3,the system kinematics equation can be obtained through configuration synthesis

where,H2and H3are 6×6 block matrix;Among them,the diagonal elements of H2are BA,BB,BC,BD,BQand 1,the only off diagonal element is located in row 6 and column 5,with the value BF,and the other elements are 0;The values of H3in row 2,column 1,row 3,column 2,row 4,column 3,row 5,column 4 and row 6,column 5 are TA,TB,TC,TDand TFrespectively,and the other elements are 0.

The dynamic equation of the projectile-artillery coupling system can be established by applying the virtual power principle

where

in which

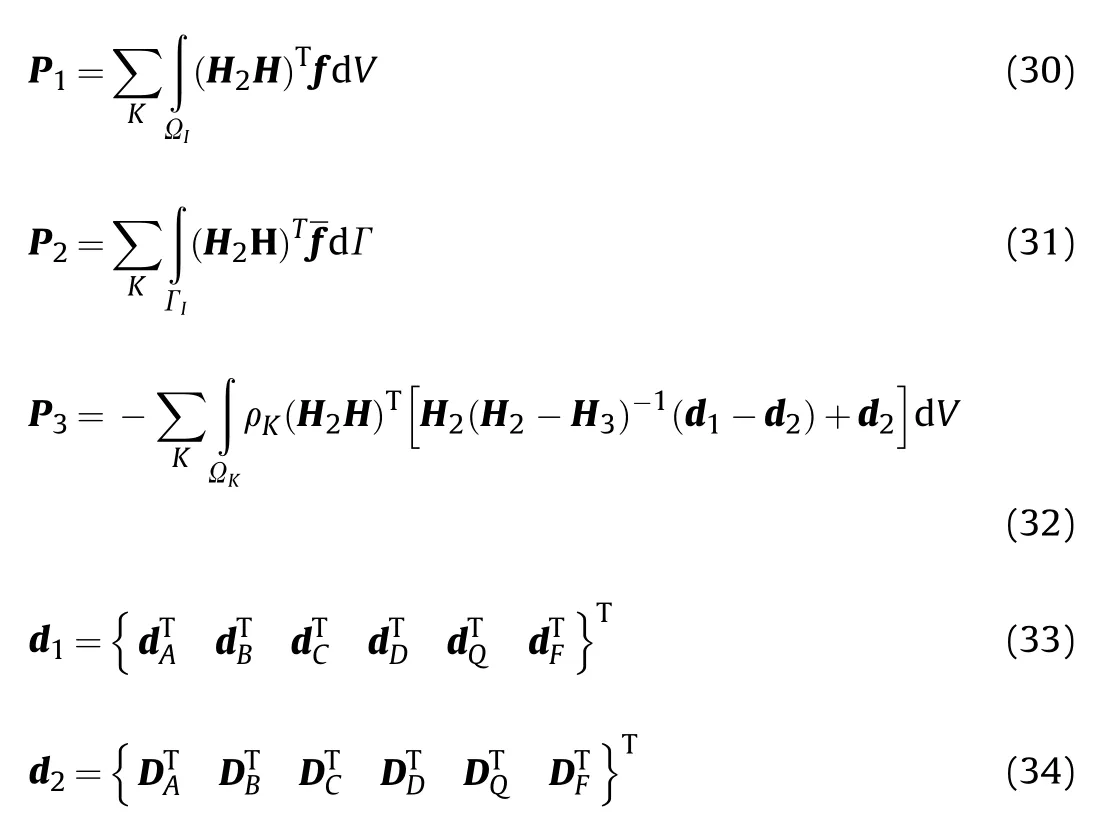
In addition to the above relative motion relationship,there are some additional constraints in the projectile-artillery coupling system,such as the constraint of rifling equation.To this end,the constraint equation is written as follows:

Then the dynamic equation of the whole system with constrained is

where c is the component of the acceleration constraint equation and λ is the corresponding constraint force.

5.The key parameter identification

By solving Eq.(36)and using the kinematic relationship similar to Eq.(21)-Eq.(23),the displacement UD,velocity.UDand angular velocity ωDand the direction pointed iDof the barrel can be obtained.Based on this,the angle and angular velocity of the barrel in Eq.(15)can be calculated by using the transformation relationship,which is recorded as follows:

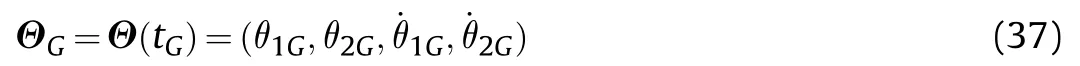
On the other hand,In Eq.(19),except vg,XGis the sum of the implicated motion of the barrel ΘGand the and its relative barrel angular motion.According to the analysis in Section 3,ΘGis a function of the initial firing condition Y0of the artillery,the structural parameter Y of the artillery and the generalized load P,which can be expressed as

The influence of artillery parameters Y on artillery firing accuracy is reflected by effecting barrel implicated angle motion ΘG.Analyzing the key artillery parameters Ypwhich has an important impact on ΘGis one of the important issue of artillery dynamics simulation analysis.

The Morris trajectory method based on the basic effect has the characteristics of global and local sensitivity analysis.Compared with other methods,the Morris trajectory method has a lower computational cost and it is still effective for parameters with very small sensitivity[32].It obtains the sensitivity of parameters through the statistical calculation of the local gradient(called basic effect)on the trajectories which are distributes in the parameter space.Morris trajectories are generated by randomly ergodically changing the values of each variable in a group of sample points.Such repetition can generate many trajectories in the parameter space,as shown in Fig.6.For each trajectory,the basic effects of each parameter can be calculated,and the relative importance of the parameters can be judged by counting the mean and standard deviation of the basic effects formed by many trajectories.

The specific steps are as follows:

(1)Determination of artillery angular motion parameters ΘGk(Y，Y0，P),(k=1，2，…，6);

(2)Generate M initial Morris trajectories;

(3)Calculate the muzzle response of each point on the Morris trajectory ΘGki(i=1，2，…，M+1);

(4)Calculate the basic effect of each point on the Morris trajectory,Ejk(j=1，2，…，N),N is the number of the Y;

(5)Obtain the mean value μ(Ejk)and standard deviation σ(Ejk)of the basic effects statistically;

(6)Obtain the key parameter Ypthat has an important impact on Θ(Y，Y0，P，t)through comparing the statistic parameters.i.e.

1)If μ(Ejk)is larger,the important of the parameter is larger;

2)If σ(Ejk)is larger,it means the parameter and the response have stronger nonlinear correlation or strong interaction with other parameters[34].

This leads to

Fig.6.Schematic diagram of Morris trajectory.

6.Firing accuracy design

6.1.Basic principles

According to the definition of firing accuracy,the covariance matrix γxCof firing accuracy can be represented as follows:

where,E(·)is the expectation of the variable(·),and there are

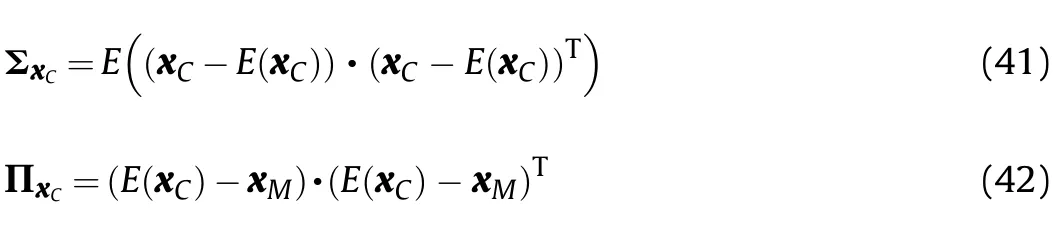
where ΣxCis the covariance matrix of the dispersion of a group of projectile burst points,andПxCis the covariance matrix of the dispersion center of a group of burst points to the target point.

Firing accuracy design is a core problem in the design of medium and long-range artillery.Its basic principle is to find the key factors affecting firing accuracy according to the firing accuracy requirement,and improve the firing accuracy of artillery through restricting or control these factors.

Eq.(16)and Eq.(39)respectively give the mapping relationship between the position coordinates of the projectile burst point and its muzzle state variables,and the projectile muzzle state variables and the key parameters of the artillery.These expressions are the basis of the design principle of artillery firing accuracy.

Assume the mean of the dispersion of projectile burst point is μxC=E(xC),the mean and the covariance of projectile muzzle state parameter are μXGand ΣXG,which can be obtained from Eq.(42)

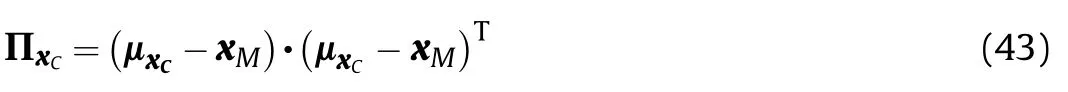
The above formulation shows that μxCis given byПxC,that is

On the other hand,if the mean and covariance of Eq.(17)are calculated,the following relationship is established.

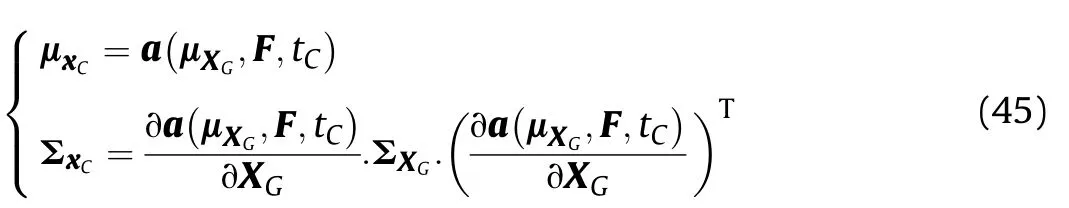
The above formulations give the mapping relationship between the μXG,ΣXGof the projectile muzzle state parameters XGand μxC,ΣxCof the burst point xCof the projectile.Investigation the first formulation of Eq.(45)and Eq.(44),it can be seen that μXGis determined by theПxC

The inverse problem of the second formulation of Eq.(50),the solution can be expressed by the following general expression:

Record the mean and covariance matrix of the artillery key parameter are μYpand ΣYp,and calculate the mean and covariance of Eq.(39),then

Finding the inverse problem of the first formulation in Eq.(48),the general solution can be obtained.

Solve the inverse problem of the second formulation in Eq.(48),the general solution also cans be obtained.

If the artillery firing accuracy requirementПxCis given,the mean value μXGof projectile muzzle state parameters can be obtained from first formulation in Eq.(45);if the covariance matrix ΣxCof firing dispersion is given,the covariance matrix ΣXGof projectile muzzle state parameters can be obtained from the second formulation in Eq.(45);if μXGand ΣXGare given,the mean μYpand covariance ΣYpof key parameters that have an important impact on firing accuracy can be obtained from Eq.(46)and Eq.(47).Therefore,Eq.(43)-Eq.(47)constitute the basic method of artillery firing accuracy design.

In practical engineering,many practical constraints and realizable problems should be considered.The following basic methods are often used.

Due to the limitation of structural design,the mean μYpof artillery key parameter Yphas the following constraints:

where μLYpand μUYpare the lower and upper limits of μYprespectively.

The constraint in Eq.(48)can be expressed by the following constraint relationship:

Due to the constraints of the actual manufacturing process conditions,the upper and lower limits of the key parameter Ypcovariance matrix are ΣUYpand ΣLYprespectively,i.e.

Assume that the relationship between the μYpand ΣYpof the key parameters Ypis as follows:

Simultaneous solutions Eq.(47)-Eq.(49)can obtain the mean μYpand ΣYpof the artillery key parameters Ypthat meet the firing accuracy requirements.The detail discussion about the inverse problem can be seen in Ref.[17].

6.2.Rifling twist design

The rifling twist ηD(xD1)restricts the rotation of the projectile around the barrel axis in the bore,and its constraint relationship is as follows:

where,rdis the radius of the land of the rifling,xD10is the coordinate of the starting position of the rifling,y(xD1)is the expansion function of the rifling,which has the following relationship with the rifling twist ηD(xD1):

The rifling twist directly affects the rotational motion of projectile around barrel axis.If y′(xD1)is constant,the motion of.φ(xD1)and¨φ(xD1)is directly proportional to the velocity.xD1and acceleration¨xD1of the projectile,and the proportional coefficient y′(xD1)/rdis both constant,and the projectile meets the condition of rigid body motion;If y′(xD1)is not constant,i.e.y′′(xD1)≠0,the rotational angular velocity and angular acceleration of the projectile around the barrel axis are not equal along the width of the rotating band,which does not meet the conditions of rigid body motion.y′′(xD1)≠0 causes the rotating band in the process of contact with the rifling,and the forced plastic extrusion along the circumferential direction of the rotating band is not uniform,which makes the rotating band deformation inconsistent,resulting in inconsistent air resistance of the flight motion of projectile.These result in increased the dispersion of xCand reduced the firing accuracy of the artillery.

The angular displacement,angular velocity and angular acceleration of xD1on the rotating band which relative to the starting point xD10are

where,Hα=1+y′2(xD1).

The maximum deformation angle δαmaxof the rotating band squeezed by the rifling in the circumferential direction during the transportation of the projectile in the bore can be calculated by Eq.(59).

Obviously,if y′(xD1)is constant,δαmax=0.

The influence of rifling twist on the extrusion of rotating band in the width direction.As shown in Fig.7,the angular displacement,angular velocity and angular acceleration of point xD1on the rotating band relative to point xD1qare respectively:

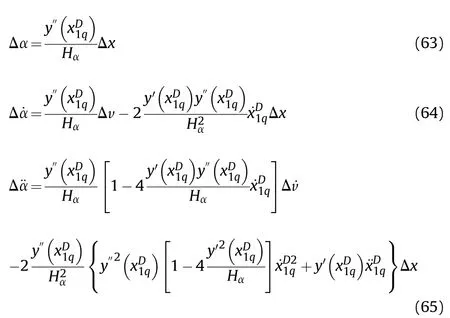
At present,the rifling can be divided into three types according to the twist form:uniform rifling,gradual rifling and mixed rifling.The muzzle twist ηD(xD1G)is determined by the gyro stability and tracking stability of the projectile flying in the air.

The expansion equation y=y(xD1)of uniform rifling is in linear form,which is characterized in that y′(xD1)is a constant on the whole rifling,that is,from the starting point xD1=xD10to the muzzle point xD1=xD1G.The analytical expression of rifling is

The expansion equation of the gradual rifling is typical in quadratic form,which is characterized by the linear change of y′(xD1)along the barrel axis in the whole rifling,that is,from the starting point xD1=xD10to the muzzle point xD1=xD1G.The analytical expression of rifling is

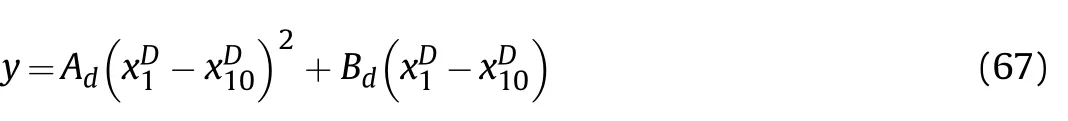
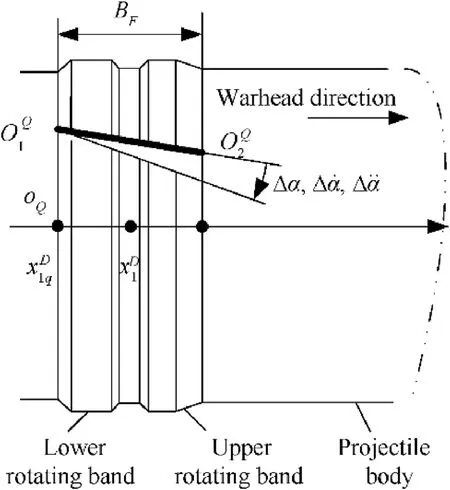
Fig.7.Schematic diagram of the relationship between rotating band and rifling。.

Mixed rifling consists of gradual rifling and uniform rifling;Generally,gradual rifling is adopted from the rifling starting position(xD1=xD10)to a position(xD1=xD1η)on the barrel,and uniform rifling is adopted from xD1=xD1ηto muzzle(xD1=xD1G).The analytical expression of rifling is

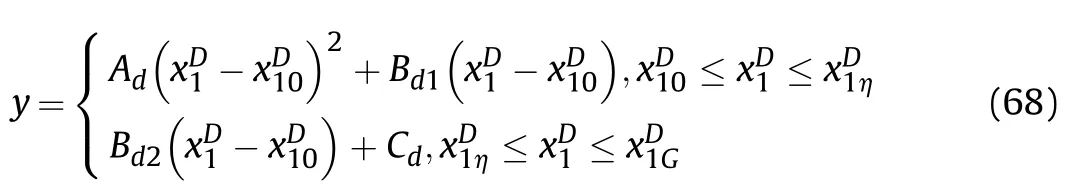
The coefficients Ad,Bd,Bd1,Bd2and Cdin Eq.(66)-Eq.(68)determine the geometric form of rifling,and the design of rifling twist is to determine these coefficients.

In addition,the shape of the rotating band has an important influence on the aerodynamic characteristics of the projectile.Fig.8 is the picture of the existence and falling off of the rotating band after the launch.Fig.9 shows the aerodynamic force diagram of the projectile with and without the rotating band during external ballistic.The research of Ref.[35]shows that the existence of the rotating band increases the resistance area of the projectile,resulting in a difference in the resistance coefficient compared with the projectile without the rotating band,and this difference has a greater effect in the small angle of attack and low Mach number.At low speed,due to the existence of the rotating band,the pressure disturbance near it is great,and then extends backward,affecting the pressure distribution on both sides of the tail and the bottom of the projectile,making the derivative of Magnus moment coefficient higher than that of the without rotating band of projectile.When the flight speed of the projectile increases to a certain extent(Ma is 1.10-1.30),the rectification effect of the rotating band on the air flow is more obvious.At this time,the derivative of Magnus moment coefficient of the projectile with rotating band is lower than that of the projectile without the rotating band.

7.Case analysis

7.1.Design of muzzle state parameters of projectile

A 155 mm vehicle-mounted howitzer launches an uncontrolled projectile with the maximum range angle and full charge.The maximum range is‖‖μxC‖‖=30 km.The position coordinate of the given target point is xM=29000ige1+60ige3(m),and

The distribution of burst point is considered as normal[13,32],and the dispersion is taken as the following three working conditions:

The task is to obtain the mean μXGand standard deviation σXGof the state parameters at muzzle XGthat meet the above firing accuracy requirements.

According to the requirements of given target point andПxC,we can draw a circle with target point oMas the center and radius R=Any point on the circle meets the requirements ofПxC.As shown in Fig.10,there are four center points on the circle,oC1,oC2,oC3and oC4all meet the requirements.

Taking oC2as an example,the coordinates of this point are

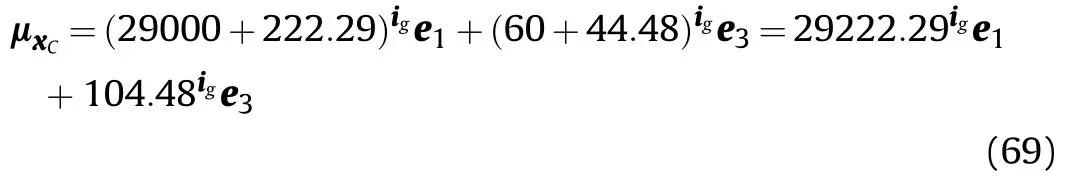
According to the dispersion center coordinates μxCgiven above,the mean μXGof projectile muzzle state parameter can be calculated inversely by applying the external ballistic equation Firstly,and then the standard deviation σXGof the projectile muzzle state variable can also be obtained.Assuming that the distribution of muzzle state parameters is normal,the range of μXGand σXGare shown in Table 1.

Three groups of results of projectile muzzle state variables meeting the firing accuracy requirements are obtained,as shown in Table 2.It can be seen that the projectile muzzle state parameters and their errors which meet the firing accuracy requirements is a solution set in the envelope space,which needs to be further optimized in combination with structural constraints,manufacturing process constraints,economic constraints and other conditions.

7.2.Identification of artillery key parameters

Also,a 155 mm vehicle-mounted howitzer launches a projectile with full charge is considered.The projectile-artillery coupling dynamics model with many artillery parameters Y can be established.To verify the effectiveness of the model,the comparison of the natural frequency,the recoil displacement and the vertical displacement at muzzle of the barrel with experiment result is carried out.During the experiment,the modal of the tube was measured by hammer,and the displacement of the tube was measured by laser acceleration sensor[35,36].The natural frequency result is show in Table 4 in which the natural frequency is dimensionless by

Table 1 The range of μXG and σXG.

Table 2 Projectile muzzle state variables.

Table 3 The dimensionless natural frequency of barrel.

Fig.8.The rotating band after launch:(a)Rotating band is complete;(b)Rotating band falls off.

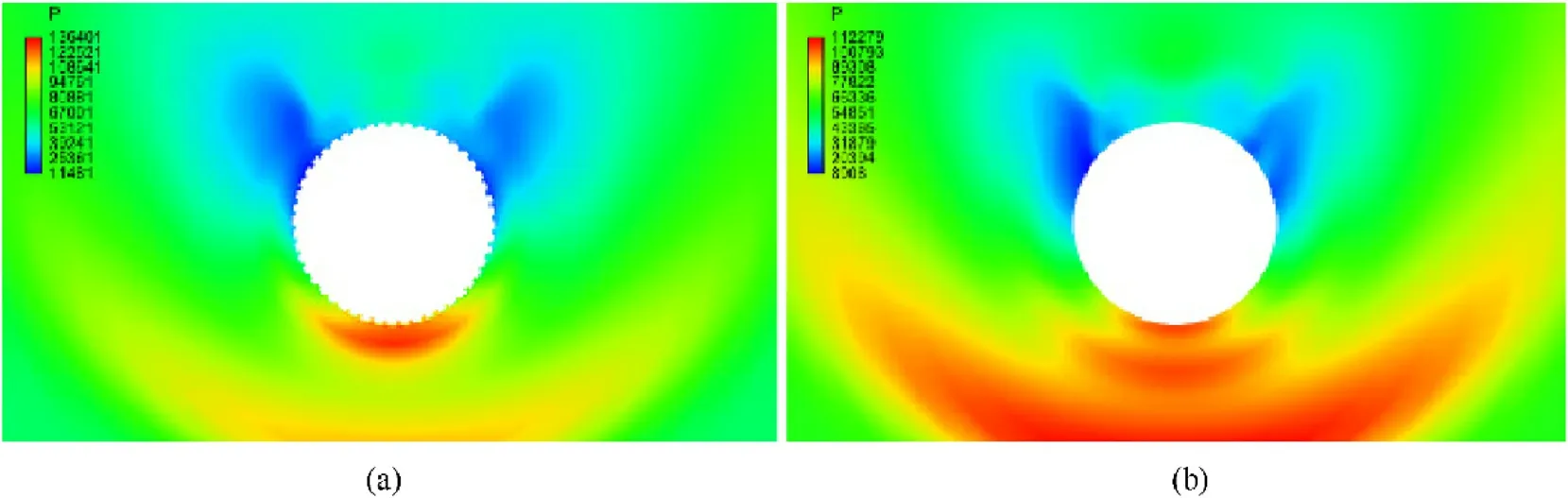
Fig.9.Cloud diagram of interface pressure distribution at the location of the rotating band:(a)With rotating band;(b)Without rotating band.

Fig.10.Relationship between dispersion center point and target point.

where A0and I0are the area and moment of inertia of the back surface of the barrel,E and ρ are the elastic modulus and density of the barrel respectively,Lsis the length of the barrel,ωiis the ith order circular frequency of the barrel.

From Table 3,we can see that the natural frequency of barrel is consistent with the experiment results.

The recoil displacement and the vertical displacement at muzzle of the barrel is shown as Fig.11 and Fig.12.It can be seen that the response of barrel during launch process is also agree with the experiment.

The Morris sensitivity analysis method given in Subsection 5.2 is used to identify the key parameters Ypthat have an important impact on ΘG=Θ(tG).The basic process is as follows:(1)All model parameter intervals are mapped and uniformly distributed to generate the initial Morris trajectory.(2)The quasi-optimal trajectory is obtained by using the Euclidean distance criterion between maximum and minimum trajectory.(3)The absolute mean and variance of the basic factors of each parameter were obtained by combining the dynamic model.(4)Identify the key parameters that affect the motion of barrel muzzle[36].According to the experience and results of previous researchers[37],the parameters of elevating equilibrator,large frame oil cylinder and seat ring,and the parameters of recoil part,cradle and overall structure are selected.41 parameters in the model of vehicle-mounted howitzer are determined as the sensitivity analysis parameters,as show in Table 4.Among them,No.1-2 are recoil parameters,No.3-9 are cradle parameters,No.10-14 are overall structure parameters,No.15-25 are elevating equilibrator parameters,No.26-35 are seat ring parameters,and No.36-41 are parameters of large frame oil cylinder.

Table 4 List of artillery parameters.

The above parameters are sampled to form a serial of trajectories,the basic effects are calculated,and the sensitivity to the muzzle motion parameters of barrel is measure by the mean valueμ(Ejk)and standard deviation σ(Ejk)of the basic effects through statistical method.The normalization results are shown in Figs.11-16,and the larger the value of μ(Ejk)and σ(Ejk),the parameter is more important.

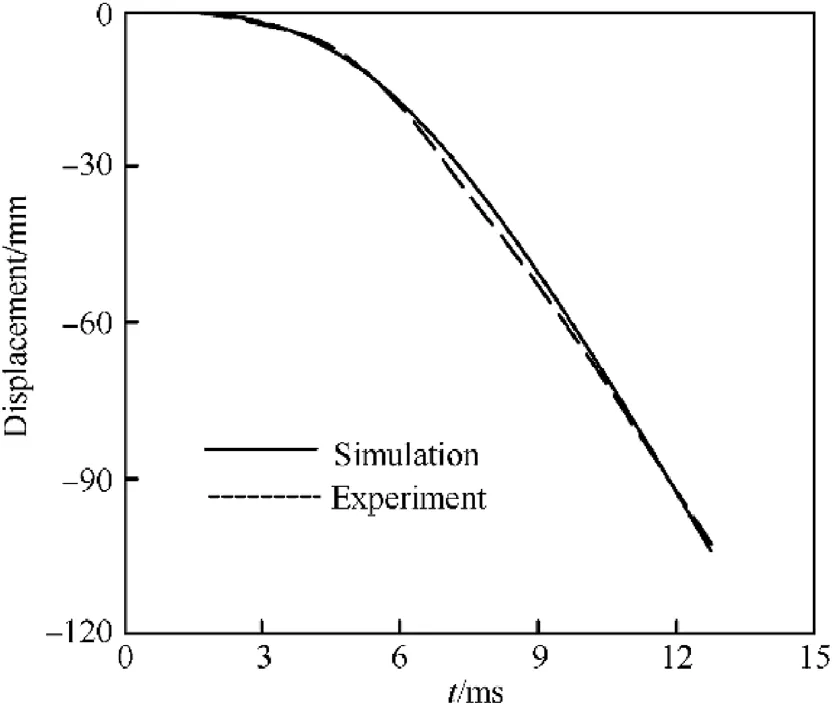
Fig.11.The recoil displacement of the barrel.

Although the accuracy of the basic effect method is not high,and cannot accurately rank the importance of parameters,but it can distinguish important parameters from non-important parameters,and can identify important parameters robustly.If we specify the parameters whose normalized parameter value is greater than 0.2 as important parameters,we can obtain the key parameters from Figs.13-18,and the key parameters for the muzzle state parameter are listed in Table 5.From the above results,it can be seen that the key parameters affecting the barrel angular displacement,barrel angular velocity and transverse velocity are similar,and the key parameters affecting the barrel elevation angular displacement,barrel elevation angular velocity and vertical velocity are also similar,and there are many key parameters.Some parameters of recoil part,cradle,overall structure,elevating equilibrator and seat ring have a great influence on the motion state of barrel,and the parameters of large frame oil cylinder have no obvious influence on each motion parameter of barrel.

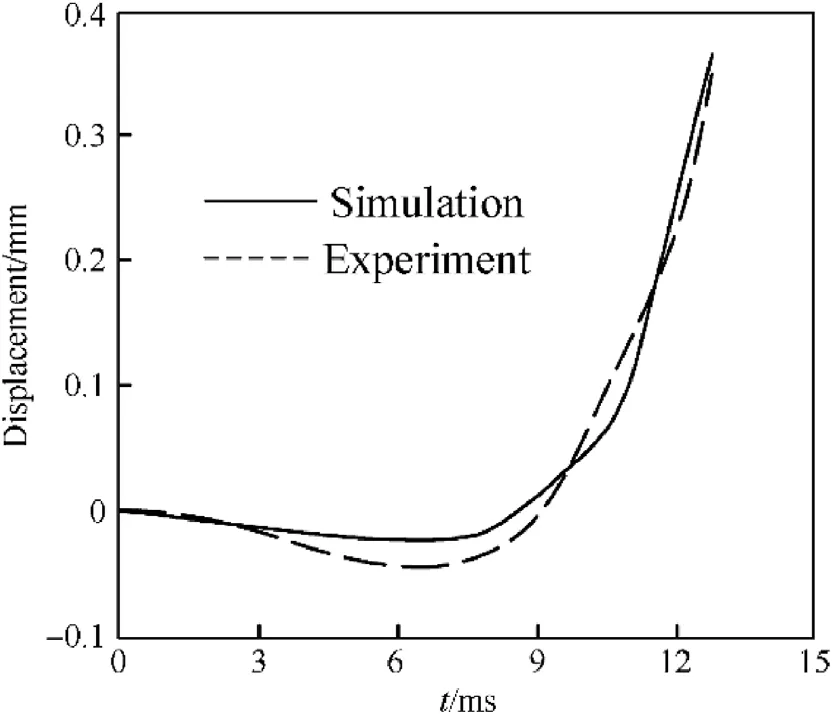
Fig.12.The vertical displacement at muzzle of barrel.

In order to facilitate the analysis,the key parameters identified above are sorted according to the components,as shown in Table 6.A total of 18 key parameters affecting the motion state of the barrel are obtained in the summary table,and the farther away from the barrel,the weaker the influence of the parameters.

Table 5 Sensitive parameters.

Table 6 Sensitive parameters of components.

7.3.Rifling twist design

(1)Influence of rifling twist on projectile rotation

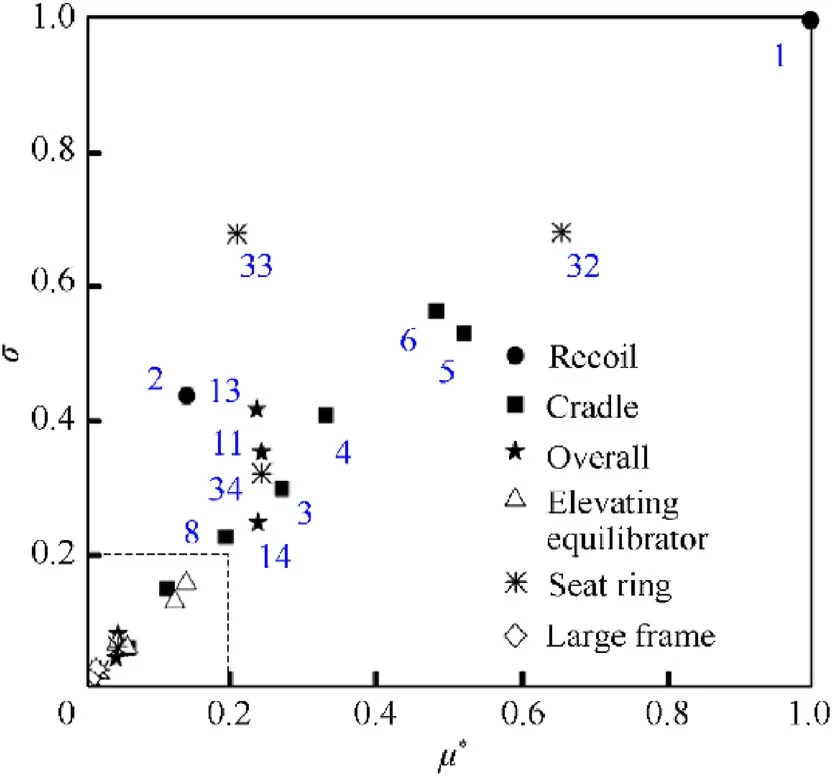
Fig.13.Muzzle angular displacement θ1G sensitivity.

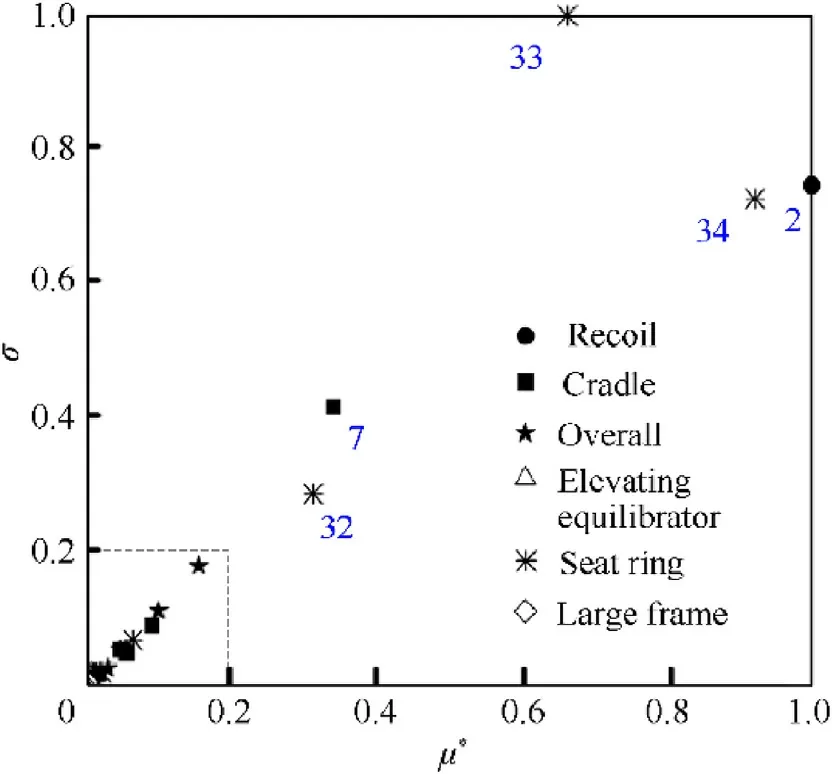
Fig.14.Muzzle angular displacement θ2G sensitivity.

Fig.15.Muzzle angular velocity sensitivity.

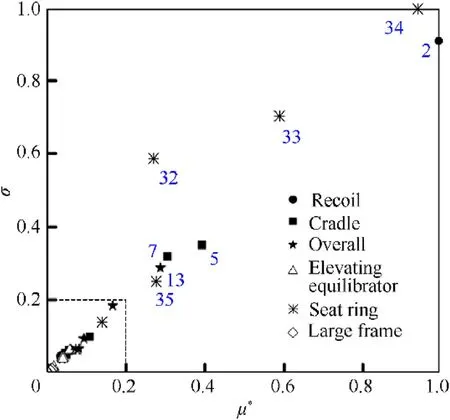
Fig.16.Muzzle angular velocity sensitivity.

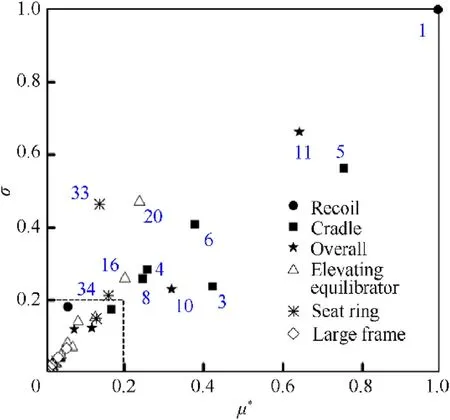
Fig.17.Muzzle vertical velocity vyG sensitivity.

Fig.18.Muzzle lateral velocity vzG sensitivity.

It is assumed that the radius of a barrel is rd,the starting point of twist is xD10,the middle point is xD1η and the end point is xD1G.The variation law of φ(xD1),.φ(xD1)and¨φ(xD1)of uniform rifling,gradual rifling and mixed rifling with projectile stroke xD1is shown in Fig.17.

(1)It can be seen from Fig.19(a)that among the three different types of rifling,the angular displacement of projectile rotating around the barrel axis at the muzzle are 14.31 rad,10.02 rad and 10.41 rad respectively.The initial twist angle of uniform rifling is 6.92◦,which is larger than that of gradual rifling and mixed rifling by 3.59◦;In terms of angle growth,the growth rate of gradual rifling is slower than that of mixed rifling,and the growth rate of mixed rifling is slower than that of uniform rifling.The angle of mixed rifling at xD1=xD1ηis continuous and smooth.(2)It can be seen from Fig.19(b)that the growth rate of the uniform rifling on the projectile rotation angular velocity starts to be fast,and the follow-up is relatively stable;The increasing speed of the gradual rifling on the angular velocity of projectile rotation is relatively stable.The action trend of the mixed rifling is similar to that of the gradual rifling before xD1=xD1η.However,at the point xD1=xD1η,due to the action of the rifling,the angular velocity has a break point,which forcibly cuts into the uniform rifling,and then is similar to that of the uniform rifling.(3)It can be seen from Fig.19(c)that the growth rate of the angular acceleration of the projectile rotation caused by the uniform rifling starts to be fast,and then decreases steadily;The growth rate of the other two rifling on the projectile rotation angular acceleration increases nonlinearly,but there is a sudden change in the angular acceleration of mixed rifling at xD1=xD1η.The reason is y′′-(xD1η)=2Ad≠y′′+(xD1η)=0,that is the second derivative is discontinuous,and the sudden change of angular acceleration will have an impact on the projectile motion,resulting in plastic deformation of the rotating and the decrease of conformal performance.(4)Based on the above analysis,in addition to the fact that the twist angle of the rifling at the initial section of the rifling is 60%higher than that of the other two rifling,the effect of uniform rifling on the projectile is the best,which is conducive to improving the conformal performance of the plastic deformation of the rotating band;The resistance of rifling with high twist angle when cutting into the rotating band is large,but the projectile motion speed in the initial section is low.This resistance can be overcome by improving the rifling strength and enhancing the toughness of the rotating band.

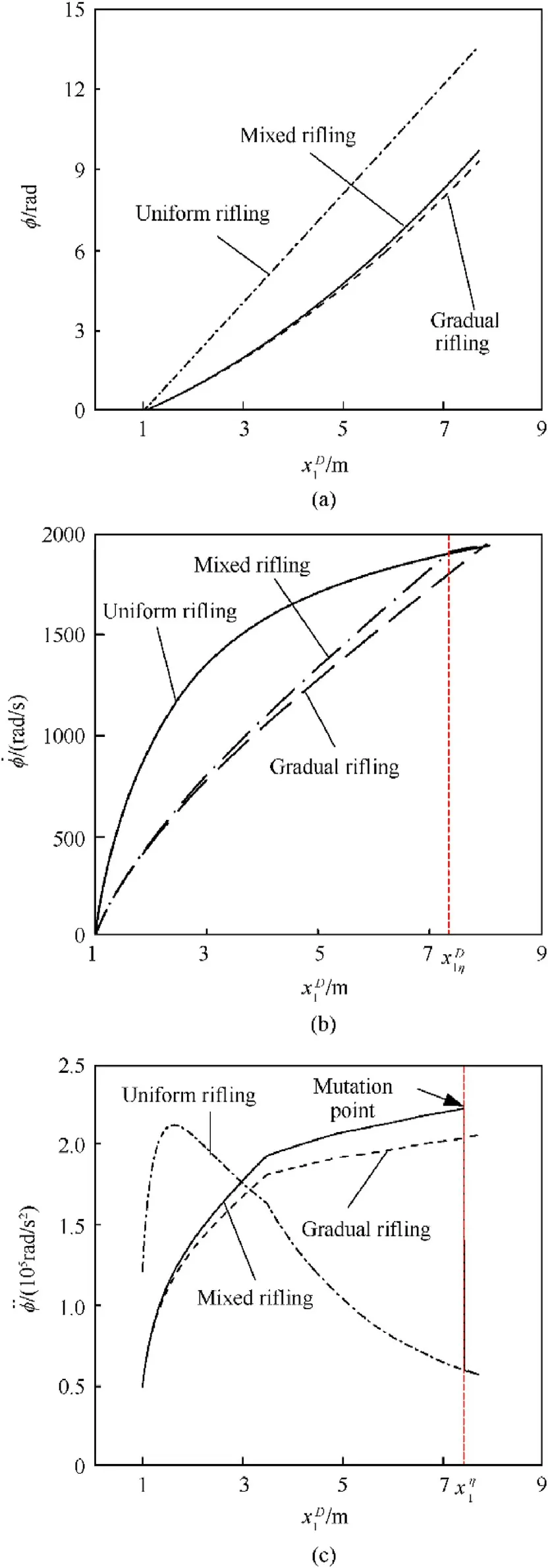
Fig.19.Comparison the φ,.φ and¨φ of rifling:(a)Angular displacement;(b)Angular velocity;(c)Angular acceleration.

(2)Effect of twist on circumferential deformation of rotating band

Under the three rifling conditions,the variation law of the angular displacement δα,angular velocity δ.α and angular acceleration δ¨α squeezed by rifling at any point on the rotating band calculated by Eq.(64)with the projectile stroke xD1is shown in Fig.20.

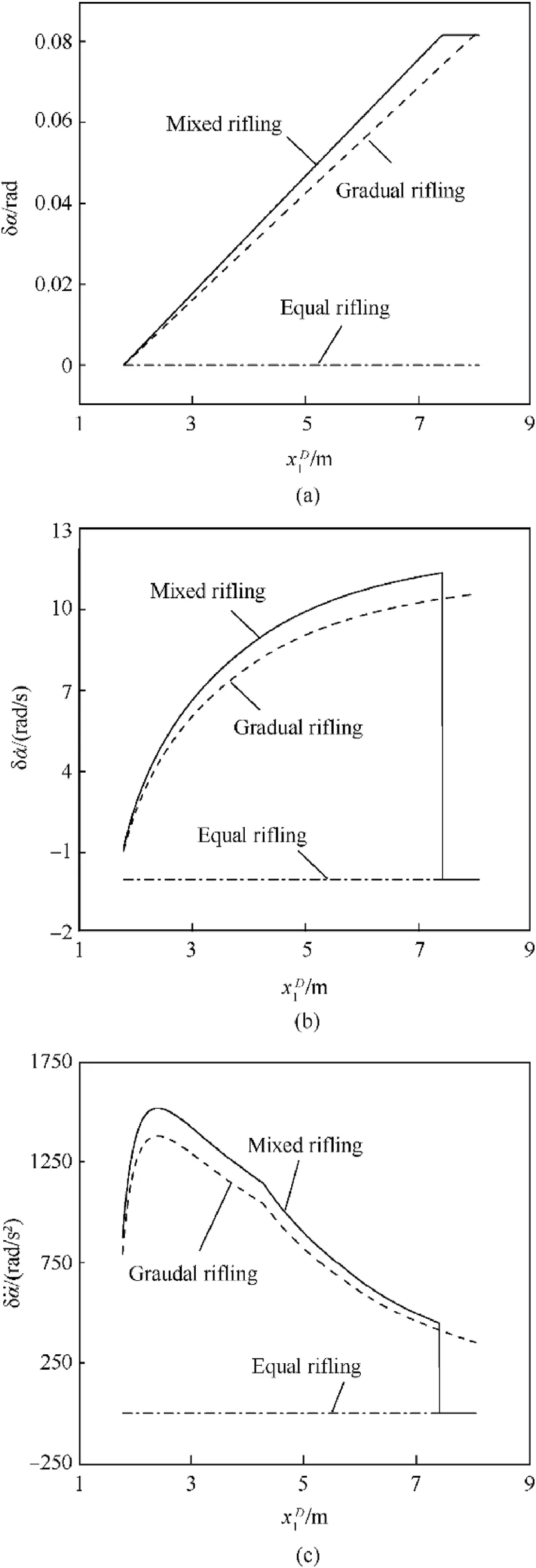
Fig.20.Circumferential extrusion δα,δ.α and δ¨α of rotating band:(a)Angular displacement;(b)Angular velocity;(c)Angular acceleration.

①δα=0,δ.α=0 and δ¨α=0 on the whole course of uniform

rifling indicates that they squeeze the rotating band evenly;

②The δα≠0,δ.α≠0 and δ¨α≠0 in the whole process of the gradual rifling show that it has an obvious squeezing effect on the rotating band.The maximum value of δα is 4.6◦,the maximum value of δ.α is 11rad/s,and the maximum value of δ¨α is 1400rad/s2.The large δα,δ.α and δ¨α will reduce the contact width between the rotating band and the vaginal,reduce the radial stiffness of the rotating band,and reduce the anti-nutation ability of the projectile;

③The mixed rifling is δα≠0,δ.α≠0 and δ¨α≠0 before xD1ηand δα=0,δ.α=0 and δ¨α=0 after xD1η.The maximum value of δα is 4.6◦,the maximum value of δ.α is δ.α=12 rad/s and the maximum value of δ¨α is δ¨α=1500 rad/s2.The extrusion angular velocity δ.α and extrusion angular acceleration δ¨α at xD1=xD1η are not smooth,which will cause the impact in the rotating band and increase the nutation velocity of the projectile;

④Based on the above analysis,the uniform rifling has the best effect on the projectile,which is conducive to improve the conformability of the plastic deformation of the rotating band,and the other two types of rifling will reduce the conformability of the plastic deformation of the rotating band.

8.Conclusions

In this paper,the dynamic equations of artillery during the whole firing process are constructed by using the topological description method.The factors that can affect the burst point of the projectiles,namely projectile on the muzzle and the state parameters of the barrel muzzle,as well as the artillery factors that affect the state parameters of barrel muzzle,are analyzed.The principle and method for improving the artillery firing accuracy are proposed,and the method is demonstrated and verified by a case of vehicle-mounted howitzer.In fact,the design principle proposed in this paper has been verified and applied in the practice of several types of artillery.The main conclusions are as follows:

(1)The key factor affecting the firing accuracy of the artillery is to control the implicated angular motion of the system before the projectile exits the muzzle during the artillery firing process,the control of the angular motion of the projectile relative to the barrel,and the control of the consistency of the plastic deformation of the rotating band during the coupling process of the projectile and the artillery(no flanging phenomenon).

(2)The key to control the coupling motion of projectile and artillery is to control the mechanical characteristics of the contact interface between the rotating band and the rifling.Therefore,the rifling twist has a very important influence on the coupling motion performance of projectile and artillery and its air flight performance.The inducement for the influence on the above performance is the initial condition of rotating band driving.

(3)As the inverse problem inherently existential multiple solutions,the application of constraints(including structural constraints,manufacturing process constraints,economic constraints and other conditions)needs to be combined with specific practice.In fact,there is no best design result for artillery firing accuracy,but only how to match the actual use of the system more closely.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the Natural Science Foundation of China(Grant No.11472137)and the Fundamental Research Funds for the Central University(Grant No.309181A880 and 30919011204).