Influence of local stiffeners and cutout shapes on the vibration and stability characteristics of quasi-isotropic laminates under hygrothermo-mechanical loadings

T.Rajanna ,K.S.Subash Chandra ,K.Venkata Rao

a Department of Civil Engineering,B.M.S College of Engineering,Bengaluru,560019,India

b Research Scholar,B.M.S College of Engineering,Bengaluru,560019,India

c Department of Mechanical Engineering,B.M.S Evening College of Engineering,Bengaluru,560019,India

d Department of Mechanical Engineering,Government Polytechnic,Bagepalli,561207,India

Keywords:

ABSTRACT s The perforated stiffened panel is generally found as a sub-component of sophisticated structures.The fundamental purpose of this panel is to withstand against buckling under complicated loading and environmental conditions.Hence,an accurate knowledge of critical buckling behaviour of stiffened panels is very much essential for a reliable and lightweight structural design.In this paper,the focus is on quasi-laminated panels with different cutout shapes of various sizes and their responses to hygrothermal environments under nonlinearly varying edge loads and is compared with the locally stiffened panels.Towards this,the modelling of the panel and stiffener is done by adopting nine-noded heterosis plate elements and three noded beam elements respectively.The stiffener formulation is suitably modified in order to take the torsional effect also into consideration along with the effect of shear deformation.Initially,the plate and the stiffener elements are treated separately,and then the displacement compatibility is maintained between them by using the transformation matrix.For a given loading and geometric discontinuity,the stress distribution within the perforated panel is highly non-uniform in nature and hence a dynamic approach has been used to calculate buckling loads by adopting two sets of boundary conditions,one set for pre-buckling stress analysis and the second set for buckling analysis.Four different quasi-isotropic stacking sequences are deliberated in this work by varying different plyorientation in each scheme.The study also addresses the effect of various parameters such as nonlinear loads,hygro-thermal loads,cutout size and shapes,position of cutout,stiffener parameters,stacking sequences,thickness of plate and boundary conditions.

1.Introduction

One of the most commonly used structural materials in industries such as aircraft,automobile,and ship building is fiberreinforced polymer composite.Since the application of these materials encountered diverse forms of usage,their service life was often marked by wear and tear.In-plane load is the only substantial load that influences these materials'overall stability and vibration characteristics.Further,the various shaped cutouts are commonly found in the composite laminates to facilitate many requirements.This significantly reduces the stiffness of the laminated panels.Furthermore,environmental factors also contribute to further reduction in stiffness of such perforated panels,resulting premature failure at lower stresses.This premature failure may be prevented by properly designing the stiffeners around the various shaped cutouts with a marginal weight penalty.As a result,an understanding of the buckling behaviour of laminated panels with reinforcement around various shaped cutouts is critical for design engineers in order to accomplish effective design under the action of hygro-thermo-mechanical loading circumstances.

Many researchers have investigated plates'vibration and buckling behaviour with/without cutouts under uniform in-plane edge compression[1,2].In the real-time scenario,uniform edge loads are very uncommon.Analysis of the laminated panels with various shaped cutouts under non-linear/non-uniform edge loads is needed to be considered in real-time applications under hygrothermal environmental conditions.Studies have also been done to analyze the vibration and buckling problems of composite panels with square/circular cutouts under different types of loading conditions without considering the effect of environmental conditions and cutout shapes[3-5].A few studies[6-8]have also been done with elliptical cutouts considering uniform edge loads.Recently,Chandra et al.[9]analysed the buckling problems of composite laminates under linearly varying and sinusoidal compressive/tensile in-plane loads with elliptical cutouts.The effect of environmental conditions and cutout shapes are not considered in their work.

The presence of stiffener significantly increases the buckling strength of the panel with a marginal weight penalty,especially in the case of perforated panels subjected to hygro-thermomechanical loading conditions.Plates with a variety of reinforcing methods are also used in aircraft fuselage and wings,ship hull and deck,offshore boiler boxes,pressure vessels,roof boxes,rockets,etc.,.Kolli&Chandrashekhara[10]used finite element technique to analyze the stiffened laminated panels under transverse loading by treating panel and stiffener separately.They utilized the transformation matrix in order to maintain the compatibility between the panel and the stiffener.Many researchers[11-17]have worked on free vibration of stiffened panels experimentally and compared analytically using finite element analysis,while works related to buckling characteristics were carried out by some researchers[18-20]but they were restricted to the plate without cutouts.Sahoo[21]investigated the vibration analysis of laminated stiffened plate with a square cutout using finite element method(FEM).A few authors[22,23]have published works on buckling characteristics of laminated panel with a reinforced square and circular cutouts subjected to uniform edge loads.The buckling responses of composite laminates with a centrally placed reinforced circular cutout under non-uniform edge loads have also been investigated by a few researchers[24-26].However,these analyses are restricted to centrally placed circular cutouts without considering the effect of different cutout shapes and their position under hygrothermal loading conditions.FRP composites deteriorate due to one or more combined forces such as hygrothermal and hygrothermomechanical buckling,extreme vibration amplitudes or high stress levels.The environmental consequences in the analysis of symmetrical and anti-symmetrical plates under hygrothermal conditions have been studied by Ram&Sinha[27,28].Biswal et al.[29,30]carried out experimental and analytical studies on composite shells under thermal conditions.Analytical studies were carried out with eight-noded doubly curved isoparametric FE having five degrees of freedom per node and were compared with the results obtained experimentally.Padhi&Pandit[31],Dafedar&Desai[32]and Das&Niyogi[33]studied the free vibration analysis of cross-ply laminated composites by considering the effect of environmental conditions(hygro-thermals).These analyses were performed without considering cutouts or openings in the panel.The hygrothermal effects on cutout panels are crucial,since they have open edges and have no edge restrictions.Ram & Sinha[34]analysed the free vibration and bending considerations in hygrothermal conditions on laminate composite surfaces,including the circular cutout.Natarajan et al.[35]have investigated the free vibration and buckling behaviour of laminated composite plates with a centrally placed circular cutout in a hygrothermal environment by using expanded finite element approach.Topal & Uzman[36],Maharudra et al.[37,38],Devarajan & Kapania[39]have also considered the effect of environmental conditions to investigate the buckling characteristics of composite laminates with a centrally placed circular/elliptical cutout.Recently,Chandra et al.[40]have carried out hygrothermomechanical vibration and buckling analysis of laminates with elliptical cutouts under localised edge loads.Furthermore,the influence of non-uniform mechanical loads and varied forms of cuts,as well as effect of local stiffeners,were not taken into account in their investigation.

In this brief literature review,it is clear that the composite laminate with cutouts are studied in-depth with regard to vibration and buckling characteristics subjected to uniform in-plane edge loads.The influence of non-uniform edge loads and environmental circumstances on the vibration and buckling of composite laminates with and without cutouts is very much limited in the literature.To the best of the authors'knowledge,no work found in the literature related to composite laminates with nonlinear edge loads in conjunction with locally reinforced cutouts under hygrothermal loading circumstances.This paper therefore examines the vibration and buckling behaviour of four different quasi-isotropic laminate schemes such as[(0+θ)/(60+θ)/(-60+θ)]s,[(0+θ)/(90+θ)/(-45+θ)/(45+θ)]s,[(0+θ)/(36+θ)/(-36+θ)/(72+θ)/(-72+θ)]s,[(0+θ)/(-60+θ)/(30+θ)/(90+θ)/(-30+θ)/(60+θ)]s.The influence of cutout shapes and locally provided stiffeners in each scheme is thoroughly studied by developing MATLAB code.The influence of various parameters such as nonlinear edge loads,hygrothermal loads,cutout size and shapes,position of elliptical cutout,stiffener parameters,stacking sequences,thickness of plate and boundary conditions are extensively investigated.

2.Theory and formulations

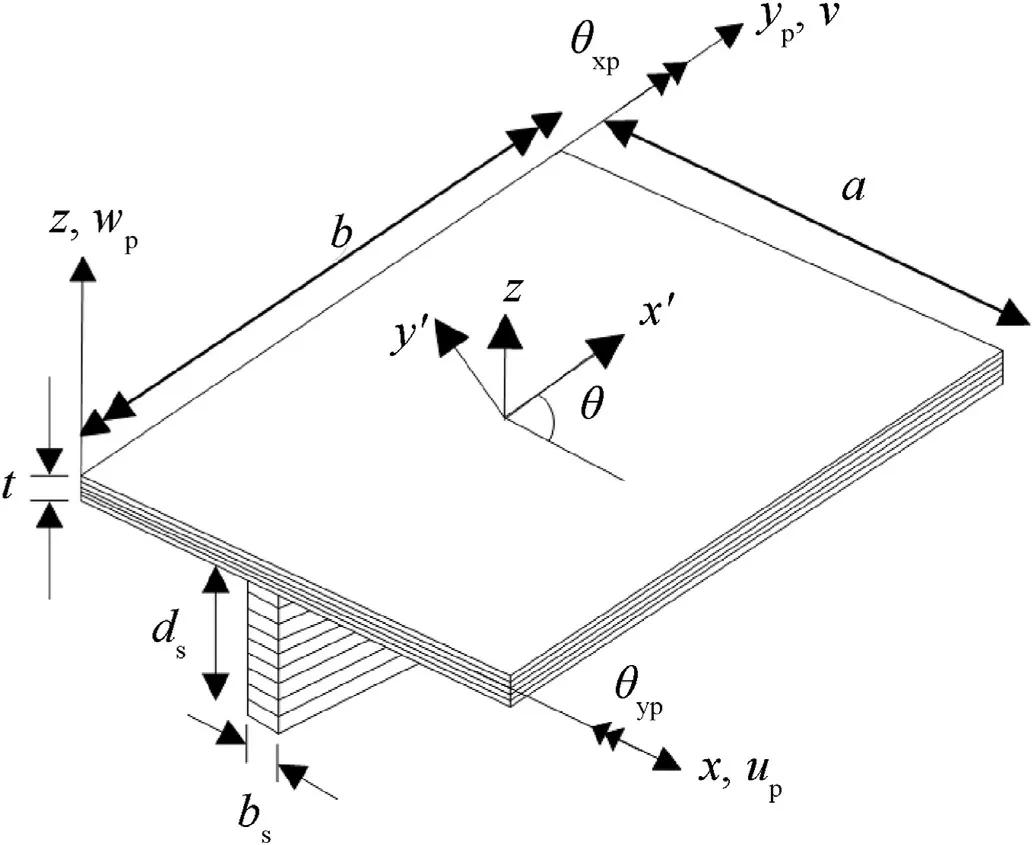
Fig.1.Geometry of the laminated panel with stiffener.

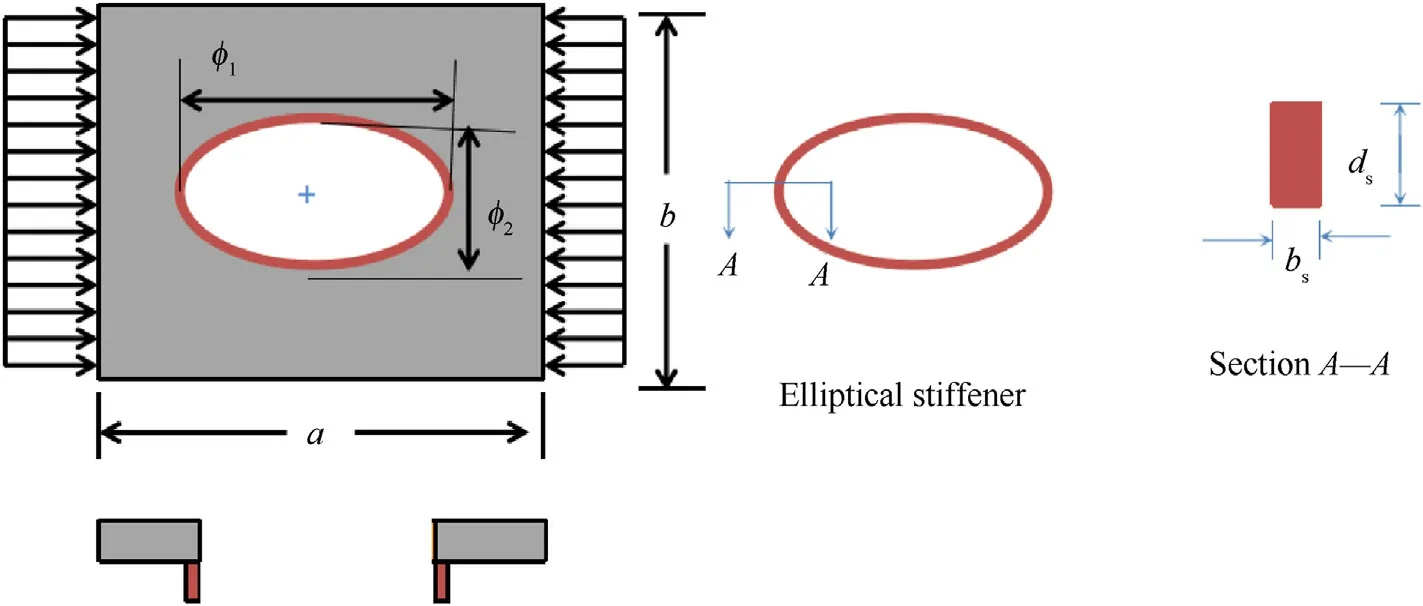
Fig.2.Geometry of the panel with a centrally placed elliptical-horizontal cutout with eccentrically placed local stiffener around the cutout.

A typical stiffened laminated plate along its coordinate definition is presented in Fig.1.The geometrical configuration of this unidirectional stiffened plate of size a x b with the plies oriented at an angle‘θ‘.The laminated panel is provided with a centrally placed elliptical cutout having a major axis of length φ1,and a minor axis of length φ2 and the stiffener of cross-section bs×dsand is attached eccentrically to the face of the laminated panel as shown in Fig.2.The plate is constructed by using 9-noded heterosis element,whereas the stiffener is modeled by employing 3-noded isoparametric beam element.A structured mesh configuration of the panel with the centrally placed elliptical cutout is highlighted in Fig.3.The mesh pattern is selected in such a way that a finer mesh is adopted in the vicinity of the cutout region by maintaining the edge skewness to a bare minimum.However,the rectangular mesh with an aspect ratio close to 1.0 is maintained in the outer region of the panel.The stiffener that is attached to the panel is positioned along the nodal line of the plate element.

In this study,the first order shear deformation theory and a shear correction factor of 5/6 is considered for the nonlinear distribution of shear strains through the thickness[1]is used to formulate the equations for composite laminates.The displacement field of a thin laminated composite plate is

Green-Lagrange's strain-displacement relation is utilized throughout the formulation.The strain displacement relation consists of two parts:(i)linear strain terms used in the derivation of the elastic stiffness matrix and(ii)nonlinear strain for the geometrical stiffness matrix.

The linear and nonlinear strains in the above equation are utilized to develop elastic stiffness and geometric stiffness matrices[1].

2.1.Constitutive relations

The composite panel's constitutive relations subjected to temperature used in the present buckling analysis are described as follows.The stress-strain relation for laminate given by equation

The constitutive matrix in the above Eq.(3)is given by

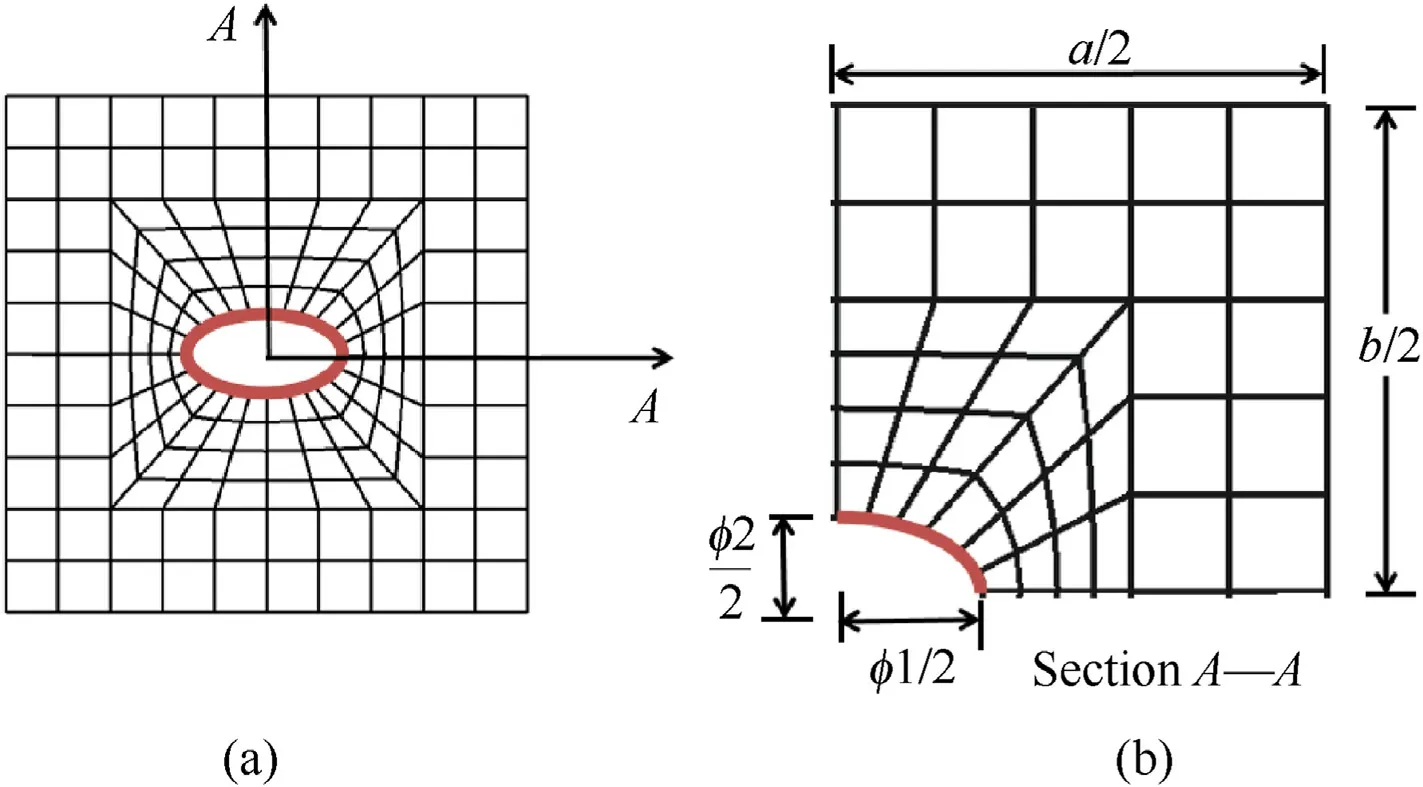
Fig.3.(a)Meshing pattern adopted for the panel with an elliptical-horizontal cutout(b)Detailed mesh pattern over a quarter panel.

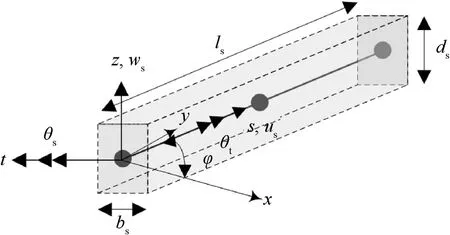
Fig.4.Geometry of stiffener with arbitrary orientation.

The each terms in Eq.(4),expressed as

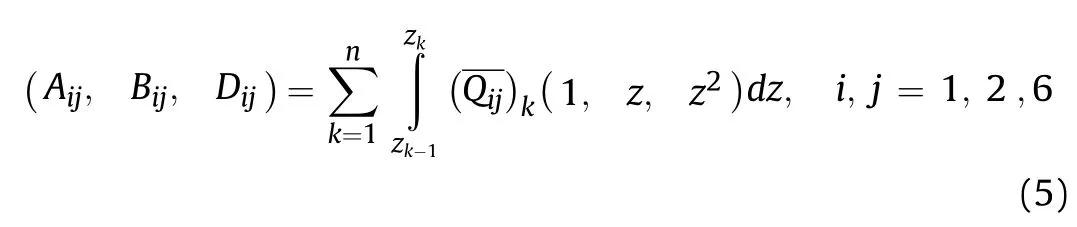
and

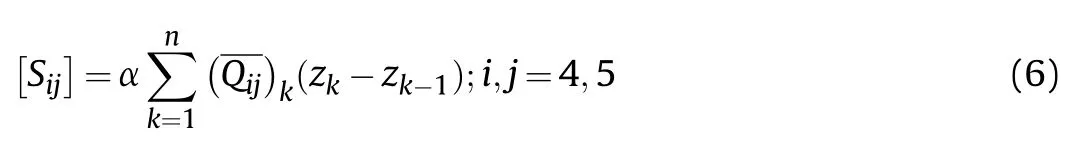
The non-mechanical force and moment resultants due to temperature are expressed as follows.

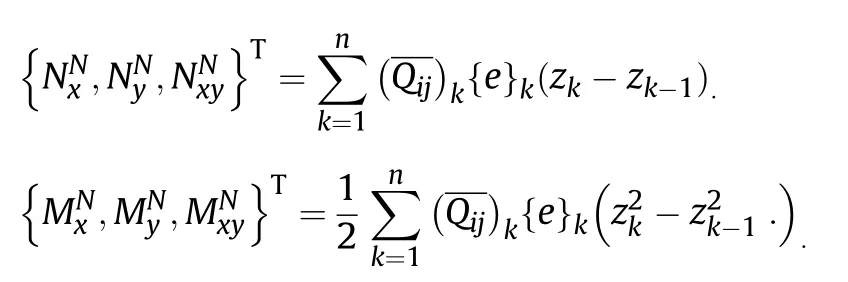
where,

in which[T]=Transformation matrix due to temperature and is given as

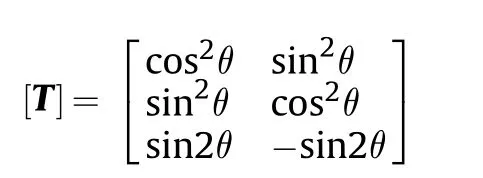
ex，ey，exyare the non-mechanical strains of the kth lamina,oriented at an arbitrary angle θ;β1，β2are the moisture coefficients of a lamina and α1，α2are the thermal coefficients in longitudinal and lateral directions.C0and T0are the reference moisture content and temperature,respectively,and Cfand Tfare the elevated moisture concentration and temperature respectively.C0and T0are assumed to be 0% and 300 K(Kelvin)respectively.

2.2.Constitutive matrix of the stiffener

Fig.4 shows the geometry of a typical stiffener of length‘ls’,width‘bs’,and has the depth‘ds’along with the positive coordinate system.The stiffener is aligned at an angle φ with respect to the global x-axis.Based on the modified beam theory[12],the displacement field at any distance z from the stiffener mid-plane is given by

where θsand θtare bending and torsional rotations along the face of t-and s-axes,and where usand wsare axial and transverse displacements.The linear strain displacement relations are given by

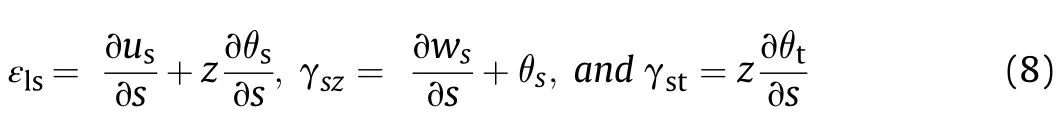
In the present formulation,the stiffener is modeled as a laminate composite.Therefore,the stress-strain relation of any kth lamina with reference to the stiffener's local axis(s-t-z)may be expressed as

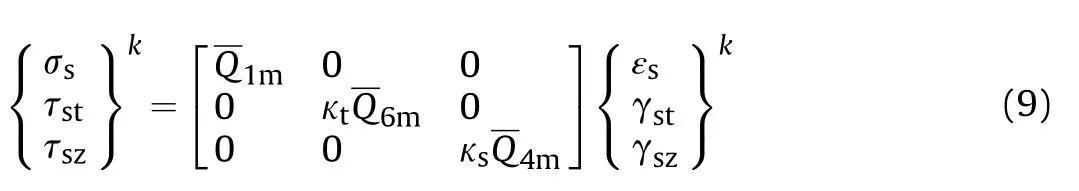
in which, ｛Ns｝T=｛Nsi，Msi，Msti，Qszi｝Tand｛εsL｝T=｛εsi，χsi，χsti，χszi｝Tare the stress resultant and strain vectors of the stiffener,respectively.The constitutive matrix of the stiffener[Ds]is shown,whose details are in Ref.[20].

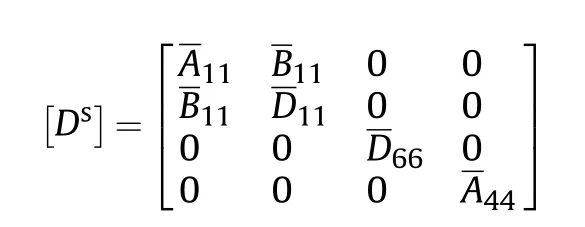
2.3.Finite element formulation

The panel is discretized by employing a nine-noded heterosis plate element.This holds five degrees of freedom(u,v,w,θxand θy)at all exterior nodes and four degrees of freedom(u,v,θxand θy)at the interior node.The isoparametric element is directed towards the natural coordinate and by using the Jacobian matrix is converted to the Cartesian coordinate system.The non-dimensional co-ordinates ξ and η of 9-noded heterosis element is depicted in Fig.5.

The following are the different matrices of the plate element needed for analysis[29,30,40]:

Eqs.11-16 represent element elastic stiffness matrix;element mass matrix;element geometric stiffness matrix due to applied inplane loads;element geometric stiffness matrix due to hygrothermal loading of the element;elemental load vectors due to hygrothermal(non-mechanical)forces and elemental load vectors due to mechanical forces and are computed by using the principle of minimum potential energy[42].

2.4.Stiffener element formulation

The stiffener is modeled by employing 3-noded iso-parametric quadratic beam element.The stiffener that is attached to the panel is positioned along the nodal line of the plate element.Applying Green-Lagrange's strain-displacement expression,the elastic stiffness matrix[kes],the geometric stiffness matrix[kGs]and the mass matrix[ms]for the stiffener element are expressed as:

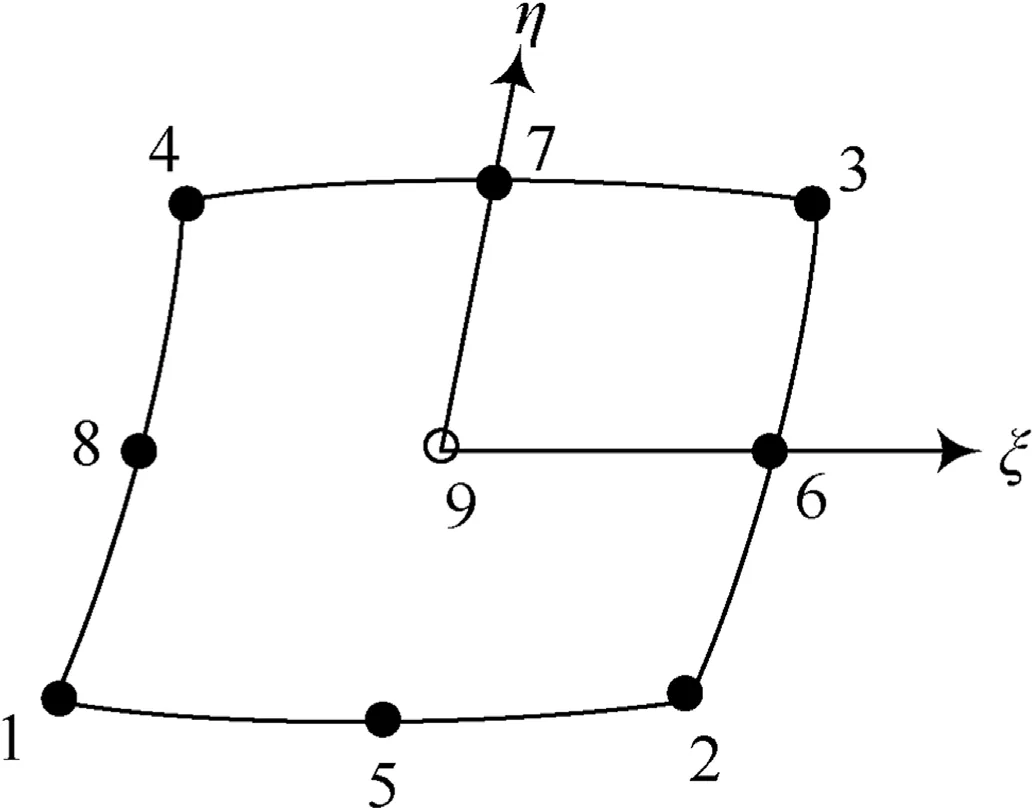
Fig.5.Nine noded quadrilateral plate element.

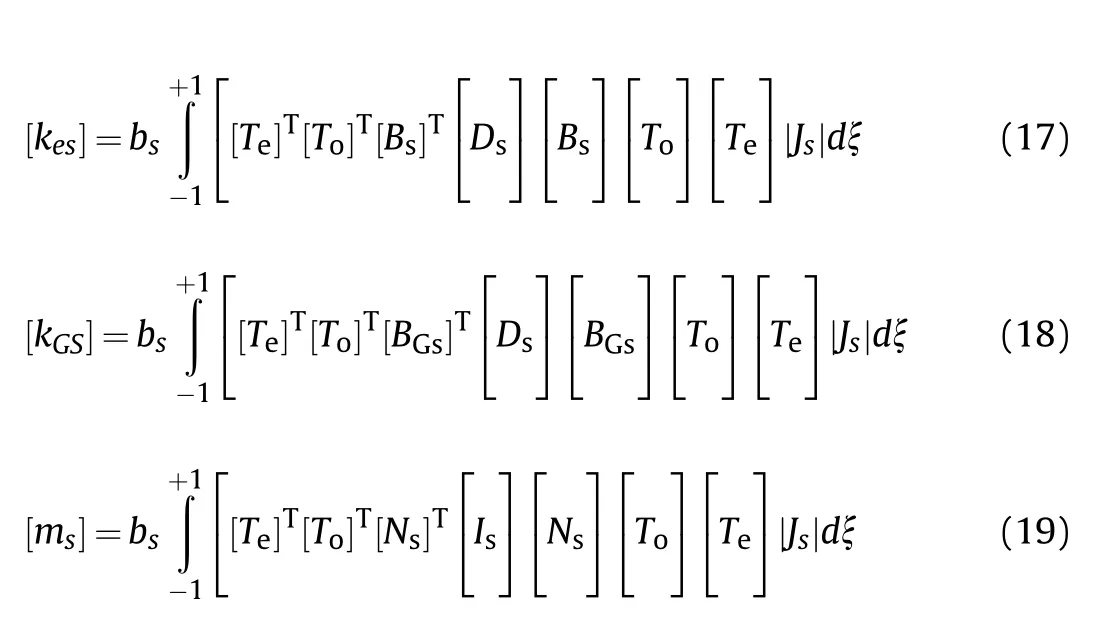
where,[Te]and[To]are matrices of transformation,taking into account the eccentricity and random orientation of the stiffener,[Bs]and[BGs]are the linear and nonlinear strain-displacement matrix and[Is]is inertia matrix of the stiffener whose details are found in Ref.[18].

2.5.Governing equation

The governing differential equilibrium equations for stiffened/unstiffened panels under hygro-thermal and in-plane edge load(P)is given by

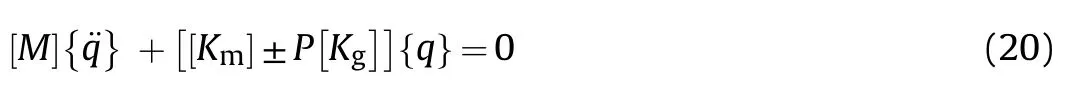
where,[Km]-the modified stiffness matrix,is a function of temperature and moisture,=[K+KHg+KTg],in which[K]is the global elastic stiffness matrix,[KHg]is the geometric stiffness matrix due to moisture,[KTg]-the geometric stiffness matrix due to temperature;[M]-the mass matrix;[Kg]-the geometric stiffness matrix,which is a function of different in-plane localized edge loading as per the present model.

The{q}and｛¨q｝terms are displacement and acceleration node vectors that must be determined according to the eigen value solution.Eq.(20)could be transformed as follows to typical eigenvalue problem

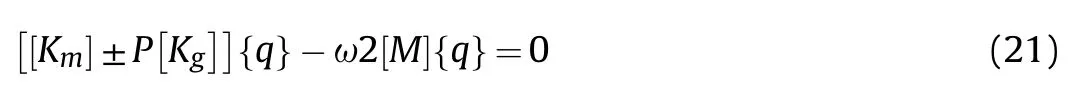
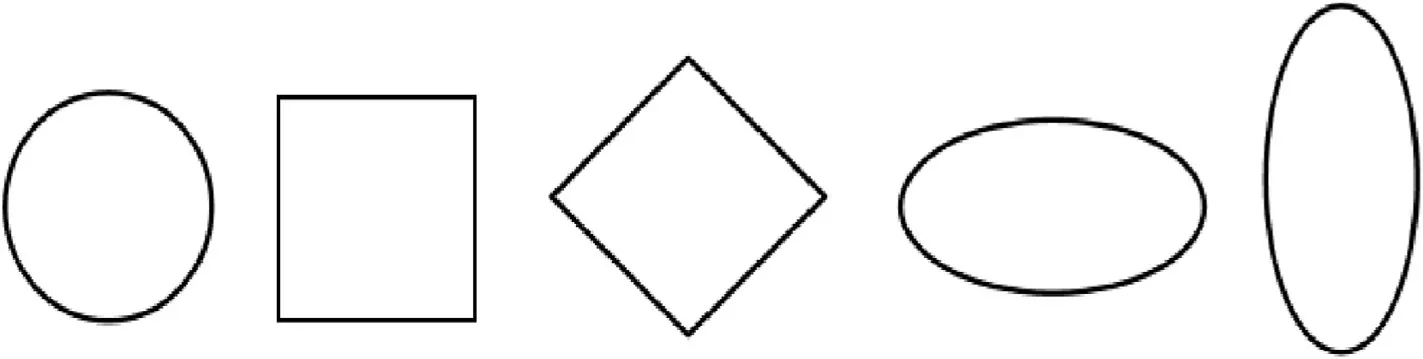
Fig.6.Cutout shapes considered in sequence circular,square,diamond,elliptical-horizontal and elliptical-vertical.

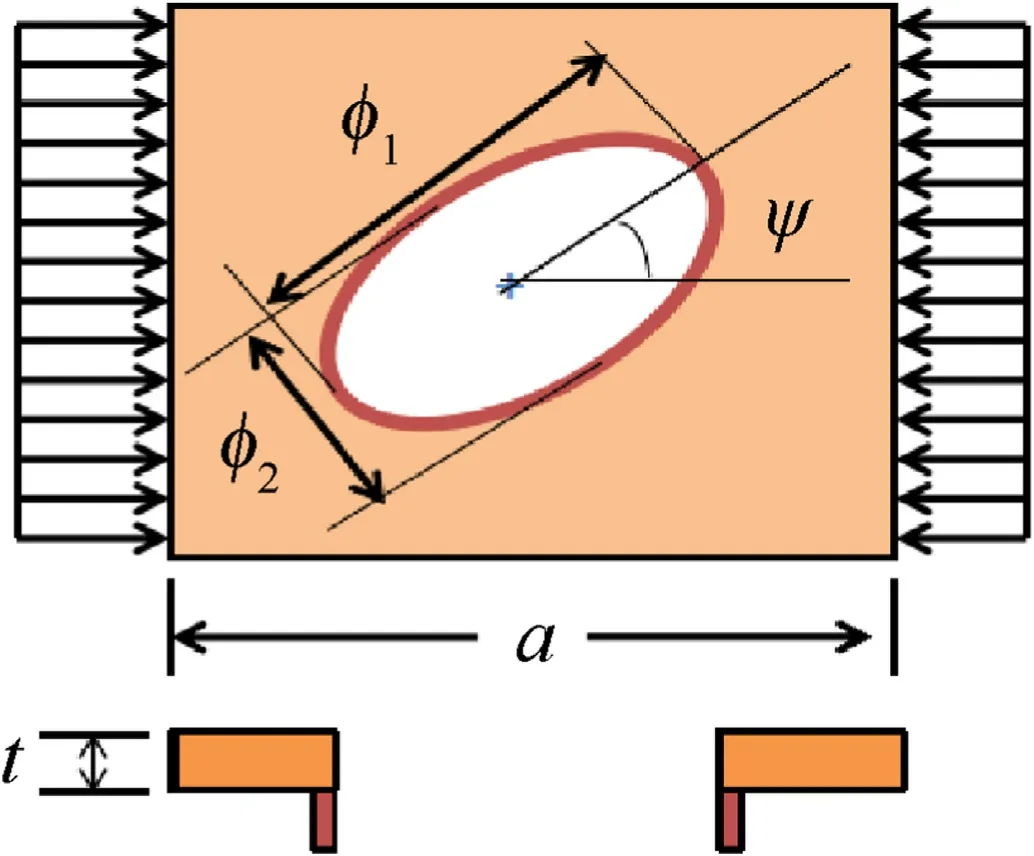
Fig.7.Panel with oblique elliptical cutout-with eccentric elliptical stiffener.

The dynamic technique is used to determine buckling loads using the aforementioned equation.In this method,the natural frequency decreases as the intensity of the in-plane load‘P’increases,eventually reducing to zero at the commencement of buckling.Buckling load is defined as a load at which the frequency drops to zero.The numerical algorithm calculates these parameters.

3.Results and discussions-problem definition and computer programming

The square panel considered in this work is thin,with thickness ratio configuration(b/t=100)and all four sides are simply supported unless otherwise specified.The different shaped cutouts such as circular,square,diamond and elliptical(both horizontal and vertical)considered in this investigation are shown in Fig.6.Even though different shaped cutouts are presented,the elliptical cutoutis considered majorly in this work.As a result,the total volume of cutout on each of the forms(circular,square,and diamond)is equal to the total volume of cutout on the elliptical cutout(φ1/b).As illustrated in Fig.7,the centrally placed elliptical cutout has major axis φ1,being the longest and minor axis φ2,being the shortest and the ellipse is oriented at an angle ψ to the x-axis.The stiffener used in this study is positioned eccentrically around the cutout forms,with stiffener depth dsand stiffener breadth bs.Unless otherwise specified,the stiffener depth to width ratio(ds/bs)is assumed to be 2 and the fibres are oriented parallel to the stiffener's longitudinal axis.Furthermore,the total volume of stiffener required for a particular cutout size is equal to the volume of material removed from the panel by the cutout section of the panel itself.As a result,for a given cutout form and size,the total volume of the plate including the stiffener remains the same as that of the plate without the cutout.The numerical algorithm computes these parameters.The different non-linearly varying edge loads considered in this work is shown in Fig.8.The non-linearly varying load acting on the load edge P0xcan be expressed in Eq.(22),wherein P is the intensity of compressive force,η=y/b(loading edge distance),and μ,λ and k determine the nonlinear variation of quadratic equation.For instance,the case of LP-1 is obtained when loading parameters are considered as μ=1,λ=1 and κ=-2.Further,as an extension,the effect of hygro-thermal environmental condition is also considered in a few problems of this work.This loading is a uniform change in temperature-humidity combination with a mechanical edge loading.The material properties considered are as shown in Tables 1 and 2.

Table 1 Elastic moduli of carbon/epoxy at different temperatures;G13=G12,G23=0.4G12,ν12=0.3,α1=-0.3×10-6/K and α2=28.1×10-6/K.

Table 2 Elastic moduli of carbon/epoxy at different moisture concentration;G13=G12,G23=0.4G12,ν12=0.3,β1=0 and β2=0.44

Table 3 Convergence of buckling(γcr)and frequency parameters(ϖ)of a panel with reinforced elliptical-vertical cutout,φ1/b=0.5,and φ1/φ2=2.

Table 4 Buckling results of a SSSS edged square panel with an elliptical cut out under uniform edge load;E11=130.0 GPa,E2 2=10.0 GPa,G12=G13=5.0 GPa,G23=3.4 GPa,and ν12=0.35.

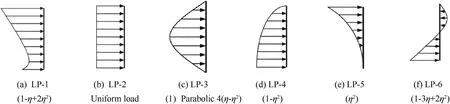
Fig.8.Types of in-plane edge loading under present study,along the edge x=0.

The critical loads and natural frequencies in non-dimensional form are as follows:

3.1.Computer programming

A computer algorithm has been developed for the present hygrothermomechanical analysis.The analysis procedure is shown in Fig.9.In the first step,the model geometry is created with elliptical cutout dimensions(φ1/b and φ1/φ2),ellipse orientation(ψ)and stiffener dimensions(dsand bs).A refined structured mesh(in Fig.3.)is generated for the model.In the second step,the mechanical properties are specified with non-uniform mechanical loading and intensities,along with specified moisture and temperature range.In the third step,the element elastic and mass matrices are obtained by using the standard procedure of finite element assembly.In the fourth step,the modified stiffness matrix[Km]is generated by clubbing elastic stiffness matrix and residual stiffness matrix,which includes temperature and moisture change.Further,the geometric stiffness matrix[Kg]is essentially a function of the in-plane stress distribution due to the mechanically applied non-uniform edge loadings.If the mechanical loading is absent,then the modified stiffness matrix is simply an elastic stiffness matrix and the geometric stiffness matrix is a function of moisture and temperature.In the last step,the eigen value problem is then solved and natural frequency and critical buckling load/temperature/moisture are determined.These steps are repeated as long as the first frequencies are degraded to zero value.At this state,load/temperature/moisture reaches the first critical values and the laminate is said to be buckled.The authenticity of the developed formulation may be verified by validating the critical loads with respect to the results available in the open literature.

Numerous examples are solved to demonstrate the effect of various types of non-linearly varying load patterns,cutout sizes,and other plates'parameters on the vibration and buckling characteristics.The selective integration technique based on the Gauss quadrature(i.e.,reduced integration(2×2)for shear stiffness terms and full integration(3×3)for bending stiffness)is employed throughout the analysis to avoid the shear locking effect.

3.2.Boundary conditions

In this study,various types of edge constraints are implemented,in which S(simply supported)and C(clamped)are used in the string of various boundary conditions.In the analysis,the buckling results are calculated in two different stages.Firstly,the prebuckling analysis is carried out in order to determine the in-plane stress distributions within the plate element.The critical buckling loads are then calculated using the in-plane stresses.

Fig.9.Flowchart of hygrothermomechanical buckling and vibration analysis procedure.

The displacement boundary condition considered for both prebuckling and buckling analyses are as follows:

Simply supported boundary condition(SSSS).

·For pre-buckling stress analysis:w=θy=0 at x=0，b;w=θx=0 at y=0，a and u=0,v=0 at two nodes along the edges x=b/2 and y=a/2 respectively.

·For buck ling analysis:u=w=θy=0 along x=0,b;v=w=θx=0 along y=0,a.

Clamped boundary condition(CCCC).

·For pre-buckling stress analysis:w=θy=θx=0 along x=0,b and y=0,a and u=0,v=0 at two nodes along the edges x=b/2 and y=a/2 respectively.

·For buckling analysis:u=v=w=θx=θy=0 al on g x=0,b and y=0,a.

3.3.Convergence and validation studies

In a finite element analysis,the convergence study is essential for proper discretization of the structure in order to obtain reasonably accurate results.To achieve this,a simply supported square panel with a centrally placed elliptical-vertical reinforced cutouts has been considered for the vibration and buckling analysis and the results are tabulated in Table 3.The eight layered laminate of(45/-45/0/90)sis considered for the panel and the ply-orientation of stiffener along the axes is considered.The stiffener is placed eccentrically around the cutout.The results from the convergence analysis shows that,total of 196 elements are essential for good convergence for both with and without stiffened panels.

3.4.Comparison study-with elliptical cutouts

A comparison study is required to validate the accuracy of the present formulation developed for solving various problems considered in this work.The effect of elliptical cutout orientation placed horizontally and vertically has been studied in this section by considering simply supported square composite laminates and the obtained results are tabulated in Table 4 along with the numerical solutions of Jain and Kumar[7].The results are also verified by the solutions obtained using the ABAQUS software and are presented within the brackets.There is good agreement between the present results and literature as well as the FE package-ABAQUS.

3.5.Comparison study of vibration and buckling-panels with stiffeners

An isotropic clamped square panel with a centrally placed single stiffener is deliberated for the free vibration problem by considering following dimensions:a=b=0.2032 m,h=0.00137 m,ds=0.0127 m and bs=0.00635 m.The material properties considered are,E=68.7 GPa,ν=0.3 and ρ=2820 kg/m3.The natural frequencies of first ten modes are tabulated in Table 5 along with the experimental results of Olson and Hazell[13]and also with the numerical solutions obtained from literature[12-15].The good correlation is observed between the present results and those with experimental as well as numerical solutions.

The comparison study is further continued for the buckling analysis of stiffened plates with two orthogonal stiffeners with several combinations of boundary conditions and the results are tabulated in Table 6 along with the results of Hamedani and Ranji[19]obtained by using FE technique.The buckling results are presented in non-dimensional form(γcr=Pcrb2/(π2D)).The dimension of the stiffener is decided based on the bending rigidity(EIs/Db)and axial rigidity(As/bt)of the stiffener,which are taken as 15 and 0.05,respectively.The numerical results of different boundary conditions agree well with the available literature.

Table 5 Natural frequencies(Hz)of clamped square stiffened panel with one central stiffener.

Table 6 Buckling parameters of a square stiffened panel subjected to bidirectional parabolic varying compression with eccentric stiffeners placed bidirectionally.

Table 7 Effect of temperature and moisture concentration on the natural frequencies(ϖ)of a SSSS edged square plate.

Table 8 Effect of temperature and moisture concentration on bucking ratios of a SSSS edged square panel.

3.6.Comparison study of vibration and buckling-panels with moisture and temperature

The comparison study is further continued to work out the effect of thermal difference and moisture concentration on the nondimensional vibration parameters of composite laminate with(0/90/90/0)layup scheme and the numerical results are tabulated in Table 7 along with the FEM solutions of[29-31,33].The material properties considered are as follows:b/t=100,E11=130 GPa,E22=9.5 GPa,G12=6 GPa,G13=G23,G23=0.5 GPa,and ν12=0.3,ρ=1600 kg/m3.The obtained numerical results establish excellent agreement with the literature.

The above same study is further continued for buckling analysis of composite laminates by considering the effect of thermal and moisture concentration and the obtained results are tabulated in Table 8 along with various authors from the literature.The material properties are the same as considered for the previous comparison study.From this study also,the present results are well matched with the numerical results those in the literature.The excellent agreement in the present FEM results using 9-noded heterosis element confirm the correctness of the formulation and computer coding.A wide variety of problems have been investigated using the validated coding,as detailed in the subsequent sections.

4.Parametric studies on buckling and vibration of laminated cutout panels with/without local stiffener

Several case studies have been examined to illustrate the effect of different cutout shapes with and without stiffeners around the cutouts subjected to various non-uniform edge loads.Unless otherwise stated,a simply supported plate with aspect ratio,a/b=1.0 and thickness ratio,b/t=100 is considered in the study.For a given stiffener direction,the fibre orientation is always considered along the axis of the stiffener and its volume is equal to the volume of material removed by the cutout portion of the panel.Therefore,for a particular cutout shape and its size,the total volume of plate including stiffener must remain same as that of the plate without cutout.Further,the total volume of cutout on each of the shapes(circular,square and diamond)is equal to the volume removed from the elliptical cutout(φ1/b).In the case of elliptical cutout,the ratio of major-axis to the width of panel(φ1/b)is taken as,φ1/b=0.5 and the ratio of major-axis diameter to minor-axis diameter is kept as,φ1/φ2=2 unless otherwise specified.

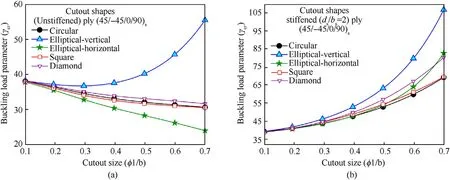
Fig.10.Variations in buckling load parameter vs.cutout sizes for various cutout shapes by considering(a)unreinforced and(b)reinforced cutouts,ds/bs=2.

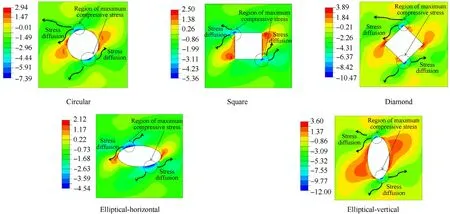
Fig.11.X-component stress contours of quasi-ply panel with different cutout shapes.

4.1.Effect of local stiffener on different cutout shapes and sizes

The effect of different cutout shapes and its sizes(i.e.,circular,square,diamond,elliptical-vertical and elliptical-horizontal)has been considered in this section to investigate the buckling characteristics of composite laminates with and without stiffeners under loading pattern-2(LP-2)and the results are illustrated in Fig.10(a)and 10(b),respectively.The variation in stress contour for different unreinforced cutout shapes can also be seen in Fig.11.The stiffeners are placed locally around the cutout shapes as explained earlier.In case of stiffener,the fibre-orientation is considered along the axis of the stiffener and an eight layered(±45/0/90)slayup scheme is considered for the panel.It is witnessed from Fig.10(a)that the buckling resistance of the panel(γcr)decreases with the increase in cutout area,irrespective of cutout shapes except in the case of elliptical-vertical,wherein the value of γcrincreases with the increased cutout area.This may be attributed to the generation of tensile stresses at wider area and also diffusion of compressive stresses towards the stiffer region with the cutout size.This increase in the tensile stress and diffusion of compressive stresses re-stabilize the panel resulting in an increase in the buckling resistance with the cutout shapes,which can be seen in the stress contours as shown in Fig.11.It is also noticed from Fig.10(a)that the circular and square cutouts have identical buckling values,wherein the difference never exceeds more than 1.4%,even in the case of locally stiffened panels.An elliptical-vertical cutout is by far the most buckling resistant of all other cutout shapes and sizes and is found to be least when applied to elliptical-horizontal cuts.However,adding a local stiffener to all the cutout shapes might improve their buckling resistance,notably in the case of ellipticalhorizontal cutout shapes,as can be seen in Fig.10(b).

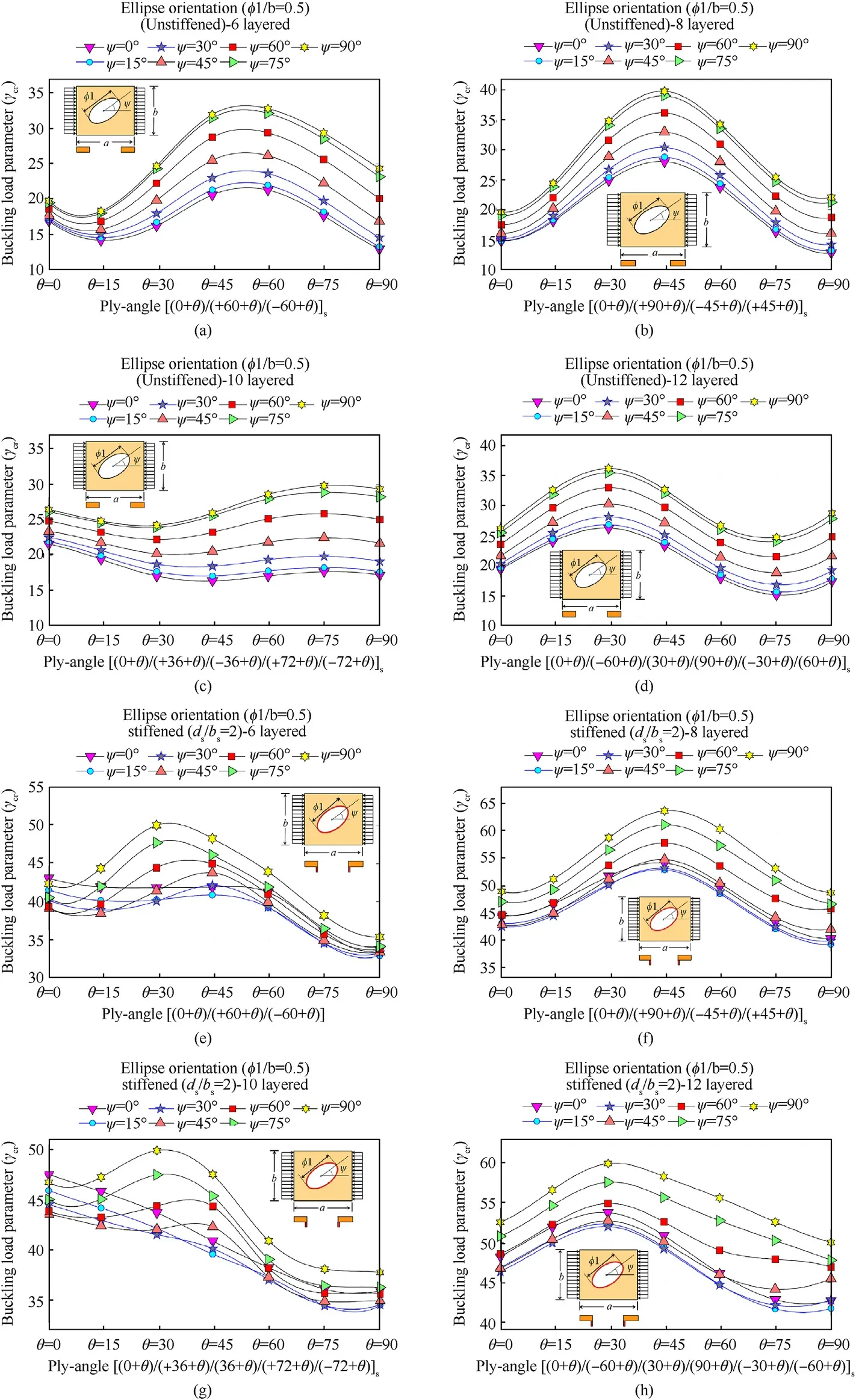
Fig.13.Variation of γcr vs.quasi-isotropic schemes without stiffener[quasi-1(a),quasi-2(b),quasi-3(c)and quasi-4(d)]and with stiffener[quasi-1(e),quasi-2(f),quasi-3(g)and quasi-4(h)].

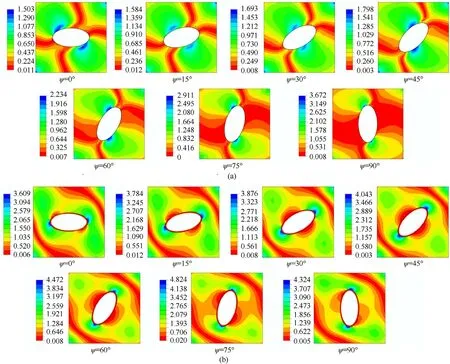
Fig.14.(a)Vonmisses stress contour of(45/-45/0/90)s quasi-ply panel with elliptical cutout(φ1/b=0.5)having different ellipse orientation ψ=0◦,15◦,30◦,45◦,60◦,75◦,90◦without reinforcement.(b)Vonmisses stress contour of(45/-45/0/90)s quasi-ply panel with elliptical cutout(φ1/b=0.5)having different ellipse orientation ψ=0◦,15◦,30◦,45◦,60◦,75◦,90◦with reinforcement.

4.2.Effect of local stiffener on different quasi-isotropic laminate schemes with elliptical cutout orientation

The effect of orientation of elliptical cutouts and ply-angles on different quasi-isotropic laminate schemes shown in Fig.12,has been investigated in this section by considering with and without stiffeners and the results are depicted in Fig.13(a)-13(h).Four different quasi-isotropic schemes,[(0+θ)/(60+θ)/(-60+θ)]s,[(0+θ)/(90+θ)/(-45+θ)/(45+θ)]s,[(0+θ)/(36+θ)/(-36+θ)/(72+θ)/(-72+θ)]s,[(0+θ)/(-60+θ)/(30+θ)/(90+θ)/(-30+θ)/(60+θ)]shave been considered and the influence of different plyorientations on each scheme is thoroughly studied by considering loading patern-2.The total thickness on each of the combinations is kept constant.

It is observed from Fig.13 that,for any given quasi-isotropic laminate scheme,the buckling resistance of the panel generally increases with the increase in ply-angle up to certain stage and thereafter decreases with a further increase in ply-angle.Also,it is observed that the elliptical orientation(ψ)significantly affects the strength of the panel and it is found to be highest when ψ=90 irrespective of quasi-isotropic layup schemes for both stiffened and unstiffened panels.It is worthwhile to note that the best chosen layup scheme on each of the quasi-isotropic laminates for both unstiffened and stiffened panels are as follows:in the case of quasi-1,(±60/0)sfor unstiffened and(30/90/-30)sfor stiffened;quasi-2,(±45/0/90)sfor both unstiffened and stiffened;quasi-3,(90/±54/±18)sfor both unstiffened and stiffened;quasi-4,(±30/±60/0/90)sfor both unstiffened and stiffened panels shows highest buckling resistance.

It is interesting to note that the panel with(±45/0/90)slayup scheme with the elliptical cutout placed vertically(ψ=90◦)has the highest buckling resistance among all quasi-isotropic layup schemes and orientation of the elliptical cutouts.In contrast,although the strength of the locally stiffened panels increases considerably in the elliptical-horizontal(ψ=0◦)orientation,it decreases slightly in all other types of cutout orientation.Fig.14(a)and 14(b)depicts the von-Misses stress contour of(±45/0/90)squasi-ply panel with and without reinforced cutouts,respectively by considering different ellipse orientations,ψ=0◦,15◦,30◦,45◦,60◦,75◦,90◦.It is observed that,as the ellipse angle ψ is varied from 0◦to 90◦,the stresses around the cutout get concentrated and move towards the major elliptical axis.As the region of stress decreases,the highest buckling resistance is found in elliptical-vertical cutout.Similar phenomenon are also found in stiffened panels but with more stress redistribution and away from the vicinity of the cutout as can be seen Fig.14(b).

Fig.15.Variations of buckling parameters(γcr)vs.stiffener depth ratios(ds/bs)with LP-1.

4.3.Effect local stiffener depth to width ratios on cutout sizes and in diverse hygro-thermo-mechanical loading condition

In this section,the panel with(45/-45/0/90)slayup scheme has been considered to investigate the effect stiffener depth ratio(ds/bs)on elliptical-vertical cutouts and the results are shown in Fig.15.As can be seen in Fig.15,the buckling resistance of the panel increases dramatically with the increase in ds/bsup to approximately 0.50-1.0,and then is practically constant with any further increase in ds/bs,irrespective of the cutout sizes.The rapid increase in the value of γcrwith ds/bsis observed to be much greater at larger cutouts compared to smaller cutouts.However,for smaller cutouts this change is essentially non-existent.

The effect of stiffener depth ratio is continued further under different combinations of hygrothermal loading conditions and the results are plotted in Fig.16 by considering elliptical-vertical cutout(φ1/b=0.5).The quasi-isotropic scheme with(±45/0/90)sis adopted for the panel.The loading pattern-2 along with hygrothermal condition is adopted for the study.It is observed from Fig.16 that the buckling resistance of the panel sharply increases when ds/bsinitially from 0.0 to 0.5 and thereafter found to be almost remain constant for further increase in the value of ds/bsfor any combination of hygro-thermal loads.It is interesting to note that the variation in the value of γcris not significant when the temperature raises from 300 K to 400 K without considering the effect of moisture,irrespective of ds/bsratios.However,there is significant variation in the value of γcris observed when the effect of moisture is considered along with the temperature.It is also interesting to note that the sharpness in the increase of γcris found to be significantly reduced when the panel is subjected to higher hygrothermal effects(400 K,1.5%C)as compared to that of the introduction of only higher thermal loads without hygral effect(400 K,0%C).The loss in the stiffness is more pronounced when both hygral and thermal loads are present.This is also true in the case of stiffened panels.

4.4.Effect of local stiffener on non-uniform loading patterns with the cutout size

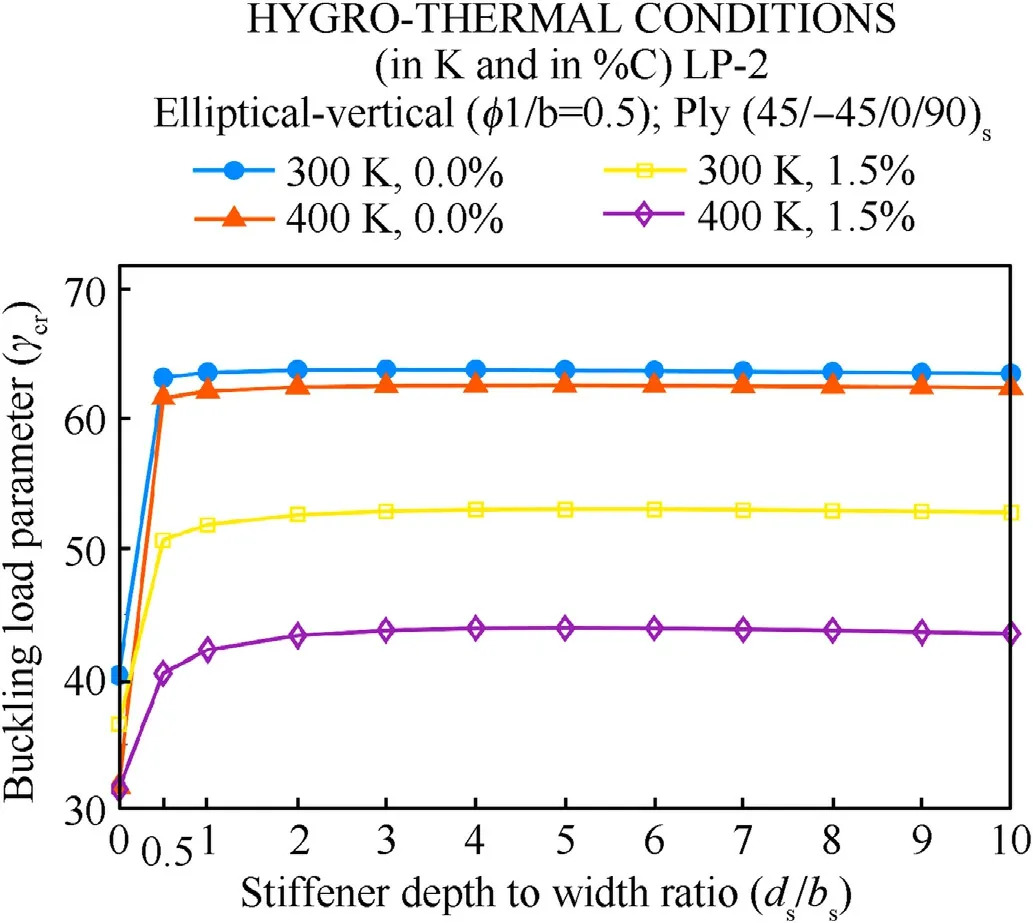
Fig.16.Influence of different combinations of hygrothermal loadings on stiffener depth ratios(ds/bs)with LP-2.

This case study presents the results on the effect of various nonlinearly varying edge loads on the buckling characteristics of composite laminates without and with stiffeners and the results are plotted in Fig.17(a)and 17(b),respectively by considering elliptical-vertical cutouts.It is witnessed from unstiffened panels that the buckling load parameter initially decreases slightly for all non-uniform loading patterns,up to φ1/b=0.4,and thereafter the buckling resistance rises with the further increase in cutout sizes as observed in Fig.17(a).While,in the case of stiffened panels(Fig.17(b)),there is no such initial fall in the buckling load parameters.In contrast,there is found to be a continuous increase in the buckling load with significantly higher buckling resistance than the unstiffened panels.The loading pattern-6(LP-6)is found to possess highest buckling resistance and LP-1 shows lowest resistance,irrespective of cutout sizes for both stiffened and unstiffened panels.This behaviour is explained by plotting stress contours for unstiffened panels under various non-linearly varying loads as shown in Fig.18.It is noticed from Fig.18 that most of the stress is concentrated near the cutout and making it the least buckling resistant whereas the LP-6 with partial tensile loading results in less stress concentration and stresses become more dispersed throughout the structure,resulting in the highest buckling strength.

The same study is further continued by considering different cutout shapes with a constant cutout size(φ1/b=0.5)and the numerical results are tabulated in Table 9 by considering various nonlinear edge loads.It is observed that the elliptical-vertical has higher buckling resistance for both stiffened and unstiffened panels,irrespective of loading patterns.Further,it also observed that the elliptical-horizontal shaped cutout shows least buckling resistance in the case of unstiffened panels whereas circular cutout is the least in the case of stiffened panels,irrespective of loading conditions.

Table 9 Comparison of γcr between unstiffened and stiffened panels with different cutout shapes(φ1/b=0.5).

4.5.Effect local stiffener on different sized cutouts under hygrothermo-mechanical loading condition

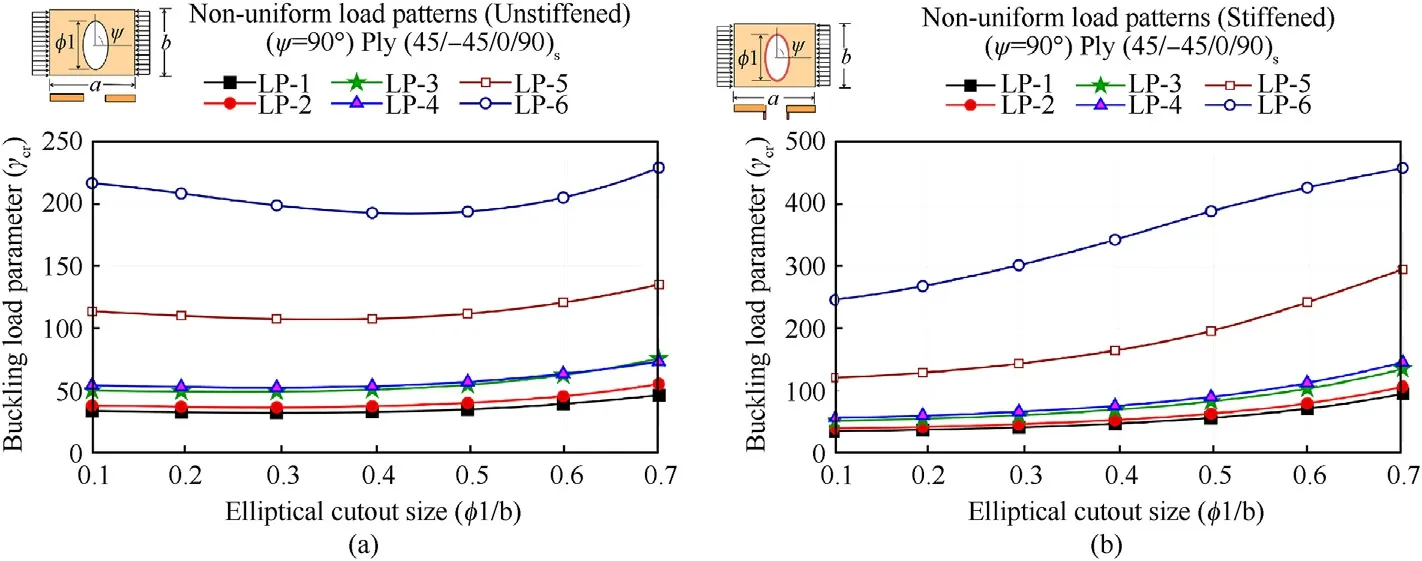
Fig.17.Variations of γcr vs.cutout sizes(φ1/b)under various non-linearly varying edge loads by considering(a)Unstiffened and(b)Stiffened(ds/bs=2)panels.

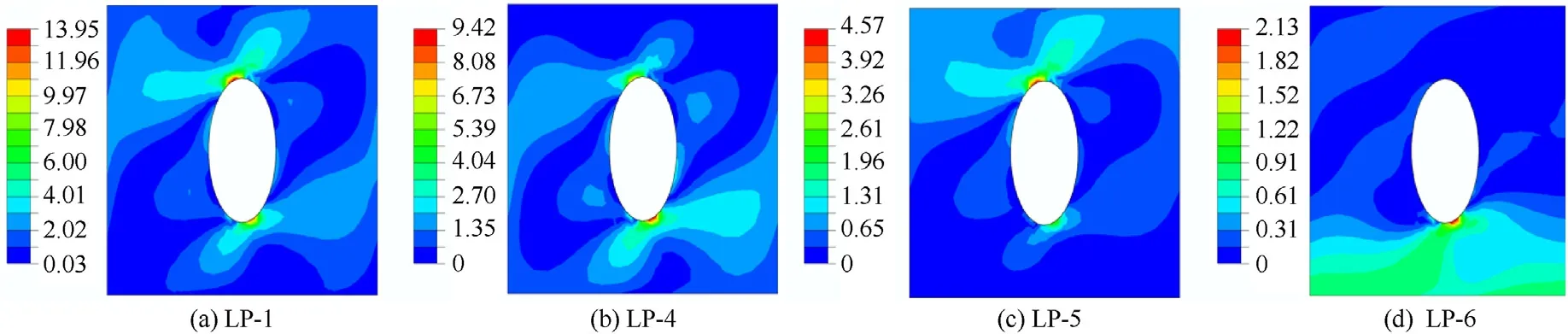
Fig.18.Vonmises stress distribution in the elliptical-vertical cutout panels(φ1/b=0.5)under various non-uniform loading patterns.

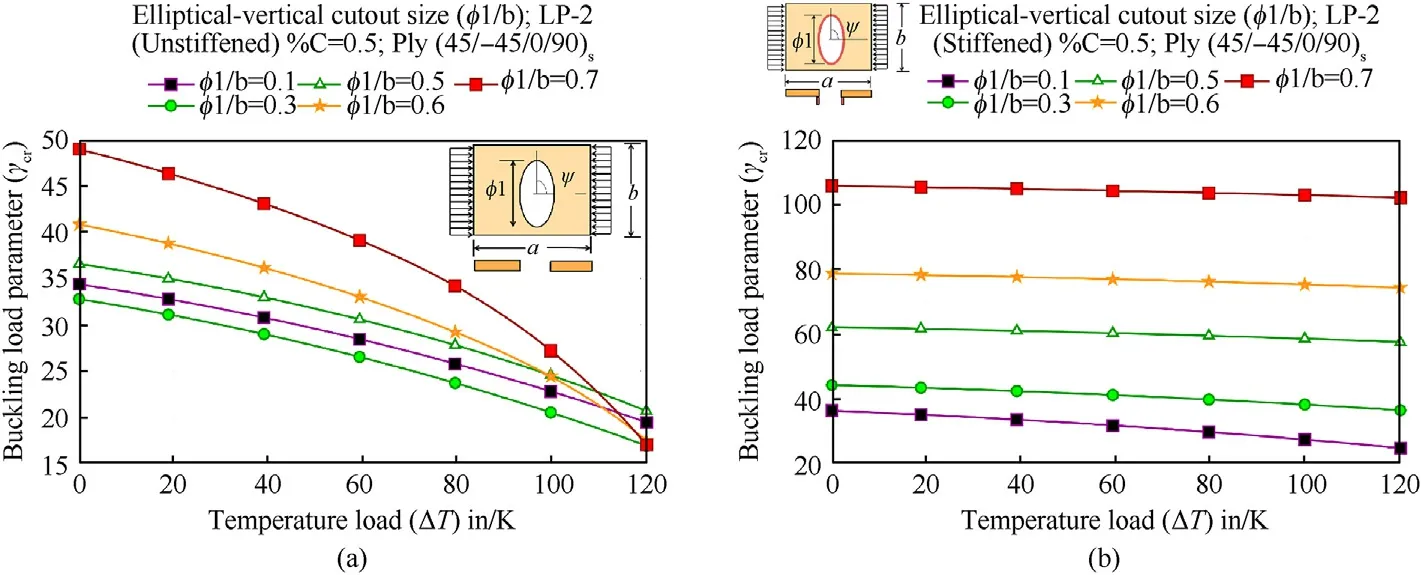
Fig.19.Influence of hygrothermal loads on different cutout ratios of(a)unstiffened and(b)stiffened(ds/bs=2)panels subjected to loading pattern-2(LP-2).

The combined effect of hygrothermal and mechanical loads(LP-2)on the buckling behaviour of unstiffened and stiffened panels with different sized cutouts has been deliberated in this section and the results are illustrated in Fig.19(a)and 19(b),respectively by considering vertically placed elliptical cutout.It is observed from Fig.19(a)that for any given cutout size,the buckling resistance of the panel decreases with the increase in temperature.The combined impact of mechanical and hygrothermal loadings in bigger cutouts is found to reduce the γcrasymptotically,accompanied by a rapid reduction in stiffness.This behaviour is practically nonexistent in stiffened panels,as shown in Fig.19(b),where the reduction in buckling resistance with temperature is not as pronounced as it is in unstiffened panels,owing to the increased stiffness of the panel caused by the local stiffener.It is also observed from Fig.19(a)that for a given temperature,the buckling resistance of the panel increases with the increase in cutout size.This increase in cutout size is found to be predominant at lower temperature only,and is insignificant at higher temperature.In case of locally stiffened plate as observed in Fig.19(b),the buckling resistance of the panel significantly increases with the increase in cutout size irrespective of temperature.Additionally,as shown in Fig.19(a),the buckling resistance of the panel rises as the cutout size increases at a given temperature.This increase in cutout size is shown to be most pronounced at lower temperatures and to be negligible at higher temperatures.However,as observed in Fig.19(b),the buckling resistance of the panel rises substantially with increasing cutout size regardless of temperature.

Fig.20.Influence of eccentricity of elliptical cutouts on(a)unstiffened and(b)stiffened panels(ds/bs=2)subjected to LP-2 at 300 K and 0.0%C.

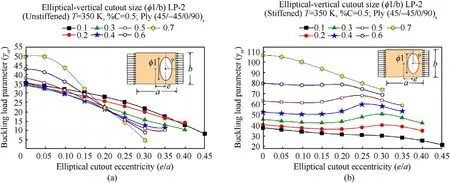
Fig 21.Influence of eccentricity of elliptical cutouts on(a)unstiffened and(b)stiffened panels(ds/bs=2)subjected to LP-2 at 350 K and 0.5%C.

4.6.Effect of hygro-thermo-mechanical load on the eccentricity of cutouts

The influence of eccentricity of elliptical-vertical cutout along xdirection(e/a)on unstiffened and stiffened panels is examined in this section and the results are illustrated in Fig.20(a)and 20(b),respectively by considering different sized cutouts.The stiffeners are provided around the elliptical cutouts and the panel is subjected to loading pattern-2(LP-2).The cutout eccentricity,e/a=0 indicates the centrally placed cutout.It is observed from Fig.20 that the value of γcrdecreases with the increase in cutout eccentricity(e/a)irrespective of cutout ratios except for φ1/b≤0.3,wherein the γcrslightly increases with the cutout eccentricity both in the case of stiffened and unstiffened panels.However,the increase in the value of γcrof the cutout eccentricity is found to be insignificant in the case of unstiffened panels as compared to that of stiffened panels.It is very important to note that in the case of unstiffened panels,the buckling resistance of the panel increases with the increase in cutout size only when the eccentricity,e/a≤0.13 and thereafter asymmetric behaviour is observed.However,this is not true in the case of stiffened panels,wherein the buckling resistance of the panel increases with the increase in cutout size irrespective of eccentricity of cutouts.This is due to the fact that stiffener around the cutout improve the edge stiffness substantially of the entire panel and therefore its buckling strength,particularly with larger cuts.

The cutout eccentricity study is further continued to examine the influence of hygro-thermo-mechanical load on the eccentricity of elliptical-vertical cutouts by considering unstiffened and stiffened panels and the results are shown in Fig.21(a)and 21(b)respectively.The panels are analysed at higher temperature of 350 K and increased moisture concentration of 0.5% along with loading patern-2(LP-2)as a mechanical loading.As shown in Fig.21(a),the value of γcrfalls continuously,as e/a increases,owing to the additional stiffness loss due to hygrothermal loads along with mechanical loading.The similar decrease in γcris also evident in stiffened panels,as can seen in Fig.21(b).However,it can be observed that due the effect of local stiffener,the influence of hygrothermal loading is considerably lesser in the stiffened panels.

4.7.Effect of hygro-thermo-mechanical loading on different thickness ratios and boundary conditions.

The effect of thickness on different boundary conditions of unstiffened and stiffened panels with elliptical-vertical cutout(φ1/b=0.6)subjected to hygro-thermo-mechanical loading has been studied in this section and the numerical results are tabulated in Table 10.The mechanical loading pattern-4 and patern-5(LP-4 and LP-5)are considered for the study along with different hygrothermal loadings.It is observed from this section that,for a given mechanical load and boundary condition,the buckling resistance of the panel significantly reduces with the increase in hygrothermalloads only in the case of thin panel configurations.But,this behaviour is not true in the case of thick panels,wherein the reduction in buckling resistance with the hygrothermal loads is almost negligible.This may be attributed to the fact that the buckling of thick panels are significantly governed by the transverse shear stiffness rather than the usual bending stiffness.It is also observed that there is a phenomenal increase in the buckling strength with the introduction of stiffener around the cutout.The introduction of local stiffener also increases the modes,which can be seen in Fig.22.The increase in the modes as well as stiffness results in higher buckling strength.

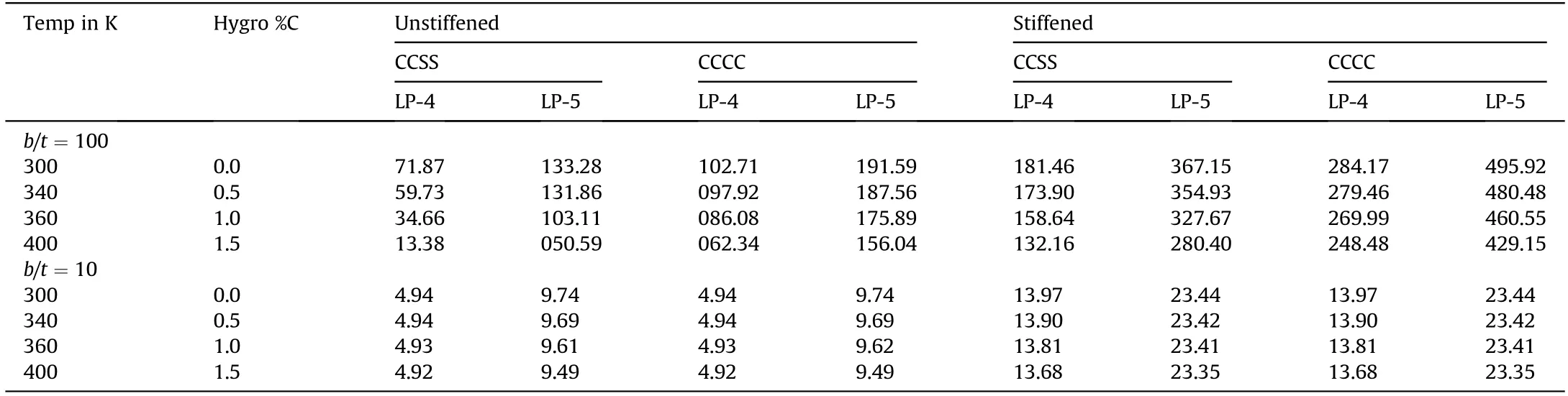
Table 10 Influence of different hygro-thermo-mechanical loads on unstiffened and stiffened panels under different boundary and thickness ratios(b/t,φ1/b=0.6 and ds/bs=2.0).

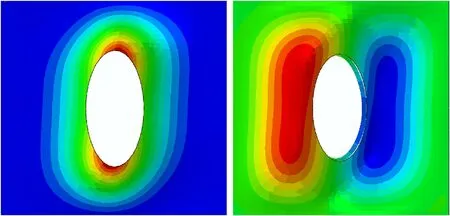
Fig.22.Mode shapes of clamped(CCCC)plate(a)unstiffened,(b)stiffened under LP-4,b/t=100,φ1/b=0.6 and ds/bs=2.0 at 300 K and 0.0%C.

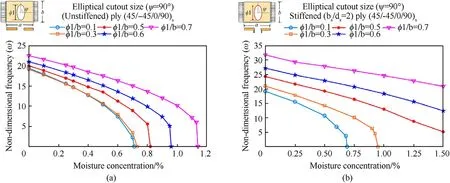
Fig.23.Influence of moisture concentration on the frequencies of quasi-2 type(a)unstiffened and(b)stiffened panels with different sized elliptical-vertical cutouts(ds/bs=2.0).

4.7.Effect of local stiffener on free vibration under hygrothermal environment

This case study deals with the free-vibration analysis of(±45/0/90)slaminated composite panel with elliptical-vertical cutouts subjected to hygral load.In this,the non-dimensional frequencies are established by keeping the temperature constant(i.e.,300 K)and the moisture concentration is gradually increased from 0% to 1.5%.The effect of moisture concentration on the vertically placed different sized elliptical cutouts with and without stiffeners is studied in this section and the results are illustrated in Fig.23(a)and 23(b)respectively.It is observed from Fig.23 that the frequency of vibration decreases with the increase in moisture concentration and becomes zero at the onset of buckling parameter.However,a significantly higher frequency of vibration is observed in the case of locally provided stiffened panel.It is important to note that for a given moisture concentration,the natural frequency increases with the increase in cutout size for both stiffened and unstiffened panels.The increased frequency is mainly due to significant reduction of mass as compared to that of stiffness of panel.

The cutout plates without stiffener initially manifest a linear drop in fundamental frequencies that drop asymptotically with worsening hygrothermal condition before attaining numerical instability,due to reduction in stiffness.However,The stiffened plates generate higher fundamental frequencies withstood more hygrothermal loads and manifest considerably longer linear drop compared to their weaker counterparts.

5.Conclusions

The present study is carried out under different case studies,keeping in view the various practical situations taken into considerations.The volume of material removed by the cutout section of the panel is used to calculate the stiffener volume.Therefore,for a particular cutout shape and its size,the total volume of the plate including stiffener must remain same as that of the plate without cutout.Further,the total volume of cutout on each of the shapes(circular,square and diamond)is equal to the volume removed from the elliptical cutout.Numerous case studies are conducted to investigate the impact of vibration and buckling on thin laminated panel under various shaped and sized cutouts with and without local stiffeners subjected to various hygro-thermo-mechanical loading situations.Based on the case studies,some useful insights have been detailed as below.

❖The panel with vertically placed elliptical cutout shows greatest buckling resistance as compared to all other cutout shapes,even in stiffened panels with a variety of cutout configurations.

❖Cutout shapes and its sizes significantly affect the buckling strength of the panel.The buckling strength of the panel decreases with the increase in cutout size,irrespective of cutout shapes except for the panel with vertically placed elliptical cutout,wherein the buckling strength increases with the increase in cutout size.

❖The buckling characteristics of both unstiffened and stiffened panels are significantly affected by the variety of quasi-isotropic lamination schemes.The eight-layered panel with(±45/0/90)slayup surpasses all other schemes,in terms of overall performance in both unstiffened and stiffened conditions.

❖For a given loading pattern,the buckling resistance of the unstiffened panel initially decreases with the cutout size upto φ1/b=0.4 and thereafter increases with the further increase in cutout size whereas γcrcontinuously increases in the case of stiffened panels.

❖The panel is strongly affected by the hygrothermal environmental conditions.When thermal and hygral stresses are coupled,the panel's buckling strength significantly decreases as compared to that of individual contributions.

❖It is found that the effect of temperature and moisture concentration is not as significant in the case of locally stiffened panels with larger sized holes as it is in the case of panels with smaller sized openings.

❖For a given cutout size,the buckling strength of the panel increases with the increase in the depth of stiffener upto certain stage and thereafter almost remains constant for further increase in the depth of stiffener.

❖The location of the cutout has a significant effect on the buckling strength of the panel.The buckling strength of the panel increases with the increase in cutout size only when the cutout is placed in the centre,but it is reversed when the cutout is placed nearer to the edge of the panel.

❖The boundary conditions and hygrothermal loads significantly affect the buckling strength of panel only in thin plate configurations,but it is trivial during thick plate configurations.

❖The frequency of vibration decreases with the increase in hygrothermal loads.However,locally stiffened panels have higher frequencies and a larger capacity of holding hygrothermal loads.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.