非等效累积损伤模型

孙振铎，吕松峰，侯东勃，张明洋

(1.河北大学 质量技术监督学院，河北 保定 071002；2.河北大学 河北省新能源汽车动力系统轻量化技术创新中心，河北 保定 071000；3.北京遥感设备研究所，北京 100854 )

随着中国工业的发展，在满足飞行器、高速列车、汽车等高速化、轻量化和高可靠性需求的同时，其机械结构中关键零部件的疲劳强度设计越来越受到重视[1-3].机械结构或零件在实际的运行过程中所承受的循环载荷并不是恒定的[4]，因此，许多学者开展了变幅疲劳研究，并基于损伤理论构建了很多累积损伤疲劳模型.

现存的大多累积损伤模型，如Miner模型[5]、Manson-Halford 模型[6]、叶笃毅模型[7]、Corten-Dolan模型[8]以及尚德广模型[9]等，均是基于“等效损伤”的原则构建出来的.冯胜等[10]则认为，材料在累积损伤过程中会遵循“非等效损伤”的原则，即材料每一次循环所产生的疲劳损伤对下一次循环的疲劳损伤会产生影响，并据此分别构建了线性[10]和非线性[11]疲劳累积损伤模型，且得到了较好的预测结果，但是，其所构建的模型计算过程较为复杂，在工程应用时会产生一定的难度，因此，有必要构建一种计算模式较为简洁的“非等效累积损伤”模型.

本文首先比较了修正Miner模型、Manson-Halford模型、Cortan-Dolan模型和叶笃毅模型的预测精度，并基于“非等效累积损伤”的原则，以Miner模型和Manson-Halford模型为基础，构建出新的“非等效累积损伤”模型，并与构建之前模型的预测结果进行比较分析.

1 试验材料与方法

基于10根45号钢疲劳试样，使用QBG-100型高频疲劳试验机，开展常温轴向拉-压加载疲劳试验，应力比R=-1，加载频率约为100 Hz，其中，6根试样用于恒幅加载疲劳试验，4根试样用于二级变幅加载疲劳试验.试样形状及尺寸如图1所示.

恒幅加载疲劳试验结果如图2所示.当σ=260 MPa时，有N>107次，故可将260 MPa视为45号钢的疲劳极限.

图1 试样形状及尺寸Fig.1 Shape and dimensions of specimen

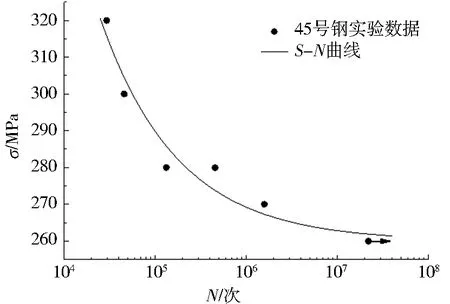
图2 45号钢疲劳试验结果Fig.2 Fatigue test results of No.45 steel

基于三参数幂函数S-N曲线模型N(σ-σf)H=C，式中C和H为材料性能常数，N代表循环次数，σ代表疲劳极限.结合试验数据可得45号钢的S-N曲线方程为

N(σ-260)1.96=7.86×107.

(1)

由式(1)，可计算出在应力水平分别为270、280、290 MPa时，对应的疲劳寿命分别为856 017、219 542、99 043 次.

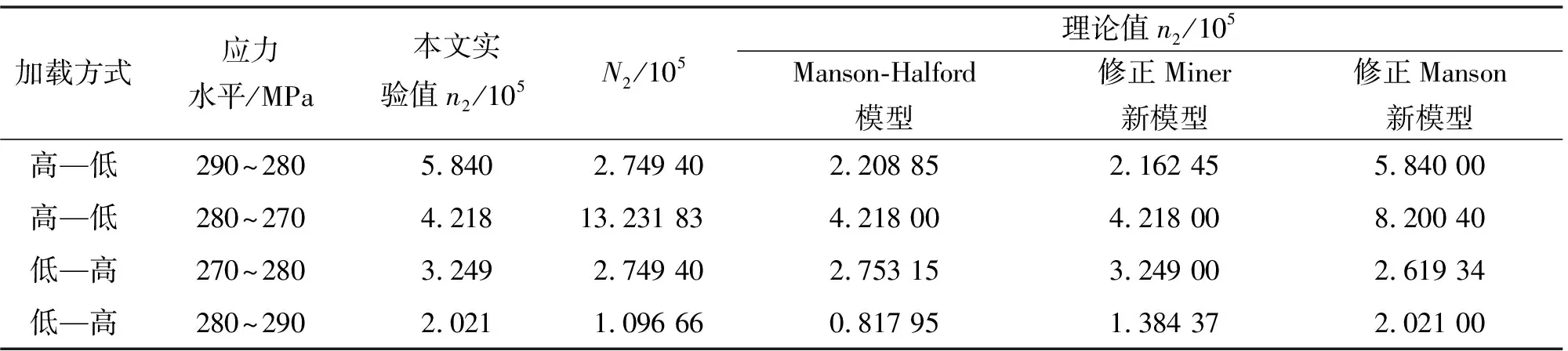
二级变幅加载疲劳试验结果及计算数据如表1所示.n1、n2分别为应力水平σ1、σ2下的循环次数，N1、N2为应力水平σ1、σ2下的疲劳寿命.

表1 45号钢二级加载试验数据

2 4种非等效累积模型的对比分析

本文进行比较分析的4种累积损伤模型见表2所示，基于45号钢试验数据得到的对比分析结果如表3所示.

表2 4种累积损伤模型

表3 基于本文45号钢试验数据的预测结果

图3为4种累积损伤模型寿命预测结果对比分析.图3可知，分别针对高—低和低—高加载顺序拟合临界损伤值以后，叶笃毅模型的预测精度要稍好于Corten-Dolan模型，Miner模型的预测精度要好于上述2种模型，其计算结果多数在2倍偏差以内，而Manson-Halford模型的预测精度要稍优于其余3种模型.

图3 4种累积损伤理论预测精度对比Fig.3 Comparison of prediction accuracy of four cumulative damage theories

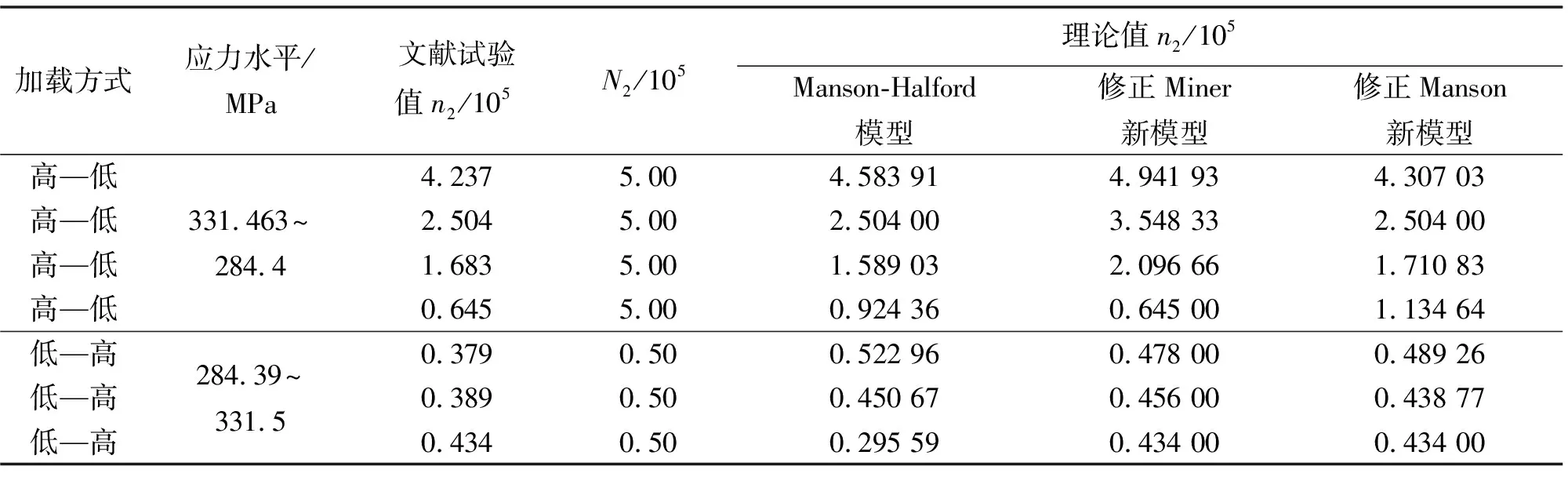
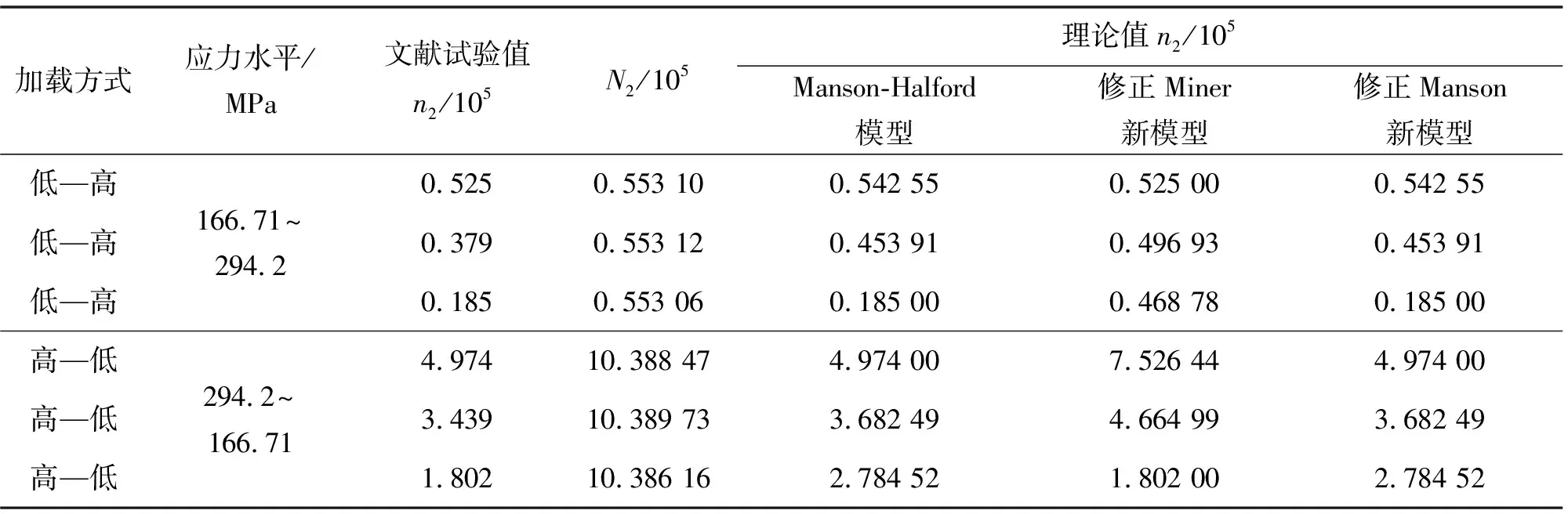
为了更进一步评估4种累积损伤模型的预测精度，分别基于文献[9]中45号钢光滑和缺口试样、16 Mn钢光滑和缺口试样的二级加载试验数据，对4种模型的预测结果继续进行对比分析，计算结果如表4～7所示.

表4 基于45号钢光滑试样试验数据的预测结果

表5 基于45号钢缺口试样试验数据的预测结果

表6 基于16Mn钢光滑试样试验数据的预测结果

表7 基于16Mn钢缺口试样试验数据的预测结果

图4～5为4种模型基于4组实验数据的预测精度对比.

a.光滑试样;b.缺口试样图4 基于45号钢的预测结果对比Fig.4 Comparison chart of prediction results based on No.45 steel

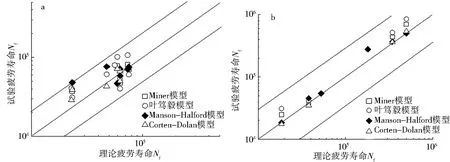
a.光滑试样;b.缺口试样图5 基于16Mn钢的预测结果对比Fig.5 Comparison of prediction results based on 16Mn steel

由图4a和图5可以发现Manson-Halford模型的预测结果均在1倍偏差以内，且理论值较其余3种模型最接近试验值，叶笃毅模型的预测结果比Miner模型和Corton-Dolan模型好；由图4b可以发现，虽然Manson-Halford模型有1个数据点不在1倍偏差以内，其理论值大于试验值，可能是因为试样表面缺陷的存在导致试样疲劳寿命较短，使试验数据具有分散性，这是偶然事件不会频繁复现，但是整体预测结果优于叶笃毅模型.综上在4种模型中，Manson-Halford模型的预测结果要优于其他3种模型.

为了保障算法拥有足够的搜索空间，需要设置较大的初始温度t0，现有设置方法主要包括构建经验公式、随机变换函数增量和均匀抽取样本法[17]。但3种方法均需事先利用个体抽样方法确定极值或方差，样本代表性较差，额外计算量过大。

3 基于非等效累积损伤的新模型构建

3.1 基于非等效损伤原则构建的修正Miner模型

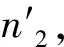
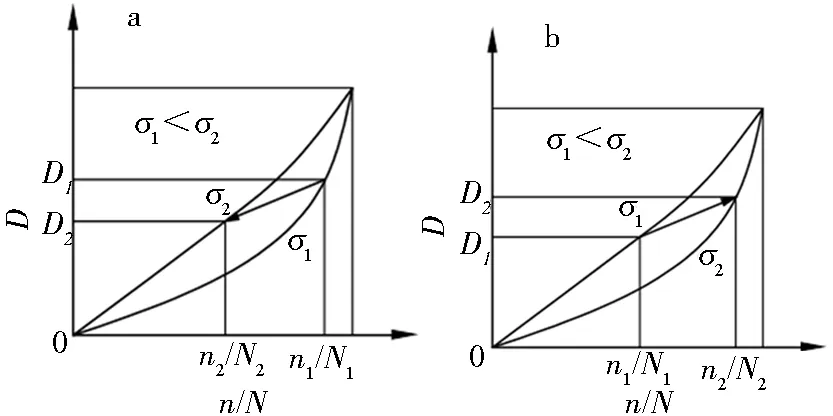
a低—高加载；b高—低加载图6 非等效累积损伤示意Fig.6 Schematic diagram of non-equivalent cumulative damage

(2)

n2/N2=1-(n1/aN1).

(3)

该模型属于线性非等效累积损伤模型.

3.2 基于非等效损伤原则的修正Manson-Halford模型

Manson-Halford[13]模型每一个循环造成的损伤为

(4)

式中，Ni是当前载荷下直至材料破坏的疲劳寿命，B和β为材料常数.

同一种材料的B是不变的，而且在多级加载公式推导以及寿命预测过程中，B没有做任何贡献，因此，将Manson-Halford模型中每一个循环造成的损伤做适当修改为

(5)

式中，Ni为当前载荷下的疲劳寿命.该模型恒幅载荷下，循环数等于疲劳寿命时，损伤值D= 1.

常幅载荷下，多个循环造成的损伤为

(6)

式中，ni为当前载荷下的循环次数.

在二级加载公式推导过程中，由一个应力水平过渡到另一个应力水平时，D不变，本文在该推导过程中，实际D值是有变化的，即D1=aD2.由此可以推导出

(7)

式中，β=0.4.式(7)即为基于非等效损伤的修正Manson-Halford模型.

多级加载情况下，参数a表示损伤非等效累积参数，其值可由试验数据拟合得到；通过大量试验数据拟合参数a，结果发现，-2.5

4 新模型预测精度分析

由4种模型的预测精度对比可知，Manson-Halford模型的预测精度最优.因此，本文将2种新模型与Manson-Halford模型的预测精度进行对比分析，基于本文试验数据的计算结果如表8所示，可以发现2种新模型的预测值更接近试验值.

表8 3种疲劳模型的寿命预测结果

图7所示为2种新模型和Manson-Halford模型的预测结果对比.从图7中可知，3种模型的预测精度基本都位于1倍偏差以内，而且修正Miner新模型和修正Manson-Halford新模型的预测精度差别不大，但是总体上修正Manson-Halford新模型的预测精度好于另外2种模型.

图7 3种模型的预测结果对比Fig.7 Comparison of prediction results of three models

为了更好地验证新模型的精度，分别采用文献[9]中45号钢和16Mn钢的光滑试样和缺口试样的两级加载试验数据进行验证，计算结果如表9～12所示.

表9 3种模型基于45号钢光滑试样的寿命预测结果

表10 3种模型基于45号钢缺口试样的寿命预测结果

表11 3种模型基于16Mn钢光滑试样的寿命预测结果

表12 3种模型基于16Mn钢缺口试样的寿命预测结果

图8～9为3种模型预测结果对比,可以看出，Manson-Halford模型的预测精度相对较低，修正Miner新模型的预测结果较好，而修正Manson-Halford新模型的预测结果相对最优.

a.光滑试样;b.缺口试样图8 3种模型基于45号钢的预测结果对比Fig.8 Comparison of prediction results of three models based on 45 steel

a.光滑试样;b.缺口试样图9 3种模型基于16Mn钢的预测结果对比Fig.9 Comparison of prediction results of three models based on 16Mn steel

5 结论

基于等效损伤原则的4种累积损伤模型中，Cortan-Dolan模型的预测结果最差，其次依次是Miner模型和叶笃毅模型，Manson-Halford模型的预测结果最优.

基于非等效损伤原则构建的2种新模型，其预测结果均要优于Manson-Halford模型，相比于修正Miner新模型，修正Manson-Halford新模型的预测精度更好.