W(2)到Kac模的0阶上同调

丁亚洲，王淑娟

(1.黑龙江大学 数学科学学院，黑龙江 哈尔滨 150080；2.上海海事大学 文理学院，上海 201306)

李超代数的上同调与代数自身的扩张理论以及表示的扩张理论密切相关.例如:相对上同调理论在Borel-Weil-Bott理论中的地位尤为重要[1]；抛物子代数幂零根基的上同调在Kazhdan-Lusztig理论中也占有重要地位[2].Kac[3-4]提出决定特征零域上单李超代数到所有不可约模的低阶上同调问题.苏育才等[5]关于李超代数slm|n和osp2|2n上同调的研究解决了Kac所提的问题.近些年来，很多人对Kac所提上述问题的素特征版本进行了研究.Wang等[6]通过对sl2|1到其Kac模以及单模的权导子进行计算, 确定了素特征域上sl2|1到其Kac模以及单模的一阶上同调.文献[7]通过研究素特征域上gl(2,F)到模李超代数W(m,3,1)的一维上同调，计算出了所有gl(2,F)到W(m,3,1)子模的导子和内导子.

众所周知，尽管素特征域上单李超代数的分类工作还没有完成，但是Witt型李超代数是一类重要的单李超代数，孙丽萍等[8]确定了gl(m,n)到Witt型李超代数的低维上同调.Sun等[9]通过对Witt代数进行子模分解和权空间分解，计算了素特征域上slm|n到Witt超代数的一阶上同调.Shu 等[10]研究了Witt型模李超代数W(2)的限制模，Duan等[11]确定了W(2)的所有单模.由于Witt型李超代数的不可约模都是Kac模的单商模，所以本文主要确定了秩为2的Witt型模李超代数W(2)到所有Kac模的0阶上同调.通过定义，计算W(2)的限制Kac模与非限制Kac模的极大平凡子模，进而决定了W(2)到限制Kac模及非限制Kac模的0阶上同调.具体地讲，当S≠0,λ=(0,2)时，W(2)到限制Kac模KS(λ)的0阶上同调空间是一维的；当S≠0或λ≠(0,2)时，W(2)到Kac模KS(λ)的0阶上同调空间都是零维的.

1 预备知识

Z-阶化限制李超代数的Kac模的定义以及0阶上同调的定义如下：

其中，uS(g)为g的S-包络代数，称这个诱导模为Kac模, 记为Kχ(λ).

根据定义, 作为向量空间

KS(λ)≅Λ(g-1)⊗FM(λ).

定义2[3]设g是李超代数，M为g-模.g到g-模M的0阶上同调空间定义为

H0(g,M)={m∈M|xm=0,∀x∈g}.

模李超代数W(2)具有下列元素构成的基：

{∂1,∂2,x1∂1,x2∂2,x1∂2,x2∂1,x1x2∂1,x1x2∂2}，

[f∂i,g∂j]=f∂i(g)∂j-(-1)|f∂i||g∂j|g∂j(f)∂i，

约定∂i(xj)=δij，其中，δij是Kronecker符号.令∂i,xj的Z-次数分别为1和-1，则

W(2)=W(2)-1⊕W(2)0⊕W(2)1

是Z-阶化李超代数.

众所周知，W(2)的任意单模都是其Kac模的商模，进而Kac模在W(2)的表示理论以及上同调理论中具有重要地位.本文尝试研究W(2)的上同调问题.根据0阶上同调的定义，一方面，W(2)是一类单李超代数，所以它到伴随模的0阶上同调是零维的；另一方面，W(2)到一维平凡模F的0阶上同调显然是一维的.虽然这是2个极端的例子，但是这意味着模的结构决定0阶上同调的结果.于是本文目标为确定W(2)到Kac模的0阶上同调.

令

h1=x1∂1-x2∂2,h2=x1∂1+x2∂2,

定义3[11]特征标S分为3类：

S(x1∂2)=0,S(h1)=0,S(h2)=2r,S(x2∂1)=1,

其中r∈F.

S(x1∂2)=0,S(h1)=r-s,S(h2)=r+s,S(x2∂1)=0,

其中r,s∈F且r,s不全为0.

对于Fp中任意数a以及整数k，引入自然数Φ(a)和Φ(a,k)使得

Φ(a)∈{0,1,…，p-1}，Φ(a,k)∈{0,1,…,p-1}，

且

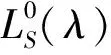
h1·vi=(λ1-2i)vi,h2·vi=λ2vi，

x1∂2·vi=i(λ1-i+1)vi-1,

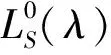
h1·vi=(λ1-2i)vi,h2·vi=λ2vi,

x1∂2·vi=i(λ1-i+1)vi-1,

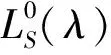
h1·vi=(λ1-2i)vi,h2·vi=λ2vi,

x1∂2·vi=i(λ1-i+1)vi-1,x2∂1·vi=vΦ(i+1).

2 主要结论

本节确定了W(2)到所有Kac模的0阶上同调.

1)当S=0或当S半单且r=s≠0时，KS(λ)具有标准基

{1⊗vi,∂1⊗vi,∂2⊗vi,∂1∂2⊗vi|0≤i≤Φ(λ1)}.

2)当S半单且r≠s或当S正则幂零时，KS(λ)具有标准基

{1⊗vi,∂1⊗vi,∂2⊗vi,∂1∂2⊗vi|0≤i≤p-1}.

任取y∈H0(W(2),KS(λ)),根据定义2可知h1y=h2y=0，即y属于KS(λ)的权为零的权空间KS(λ)0.于是H0(W(2),KS(λ))⊆KS(λ)0.因为

h1·(1⊗vi)=(λ1-2i)(1⊗vi),h2·(1⊗vi)=λ2(1⊗vi),

h1·(∂1⊗vi)=(λ1-2i-1)∂1⊗vi,h2·(∂1⊗vi)=(λ2-1)∂1⊗vi,

h1·(∂2⊗vi)=(λ1-2i+1)∂2⊗vi,h2·(∂2⊗vi)=(λ2-1)∂2⊗vi,

h1·(∂1∂2⊗vi)=(λ1-2i)∂1∂2⊗vi,h2·(∂1∂2⊗vi)=(λ2-2)∂1∂2⊗vi,

所以有下列结论：

1)当S=0时，KS(λ)0可由下列元素线性张成

δλ2=01⊗vΦ(λ1,0),δλ2=1∂1⊗vΦ(λ1,-1),δλ2=1∂2⊗vΦ(λ1,1),δλ2=2∂1∂2⊗vΦ(λ1,0)，

其中，若k∉{0,1,2,…，Φ(λ1)}，约定vk=0.

2)当S正则幂零且r=0时,KS(λ)0具有标准基

{δλ2=01⊗vΦ(λ1,0),δλ2=1∂1⊗vΦ(λ1,-1),δλ2=1∂2⊗vΦ(λ1,1),δλ2=2∂1∂2⊗vΦ(λ1,0)}.

3)当S正则幂零且r≠0时,λ2∉Fp，于是KS(λ)0=0.

4)当S半单时，λ1∉Fp或λ2∉Fp，于是KS(λ)0=0.

下面只需考虑S=0或者S正则幂零且r=0 两种情况.

1)设S=0.任取y∈H0(W(2),KS(λ)),不妨设

y=a1δλ2=01⊗vΦ(λ1,0)+a2δλ2=1∂1⊗vΦ(λ1,-1)+a3δλ2=1∂2⊗vΦ(λ1,1)+a4δλ2=2∂1∂2⊗vΦ(λ1,0).

故

0=∂1·y=a1δλ2=0∂1⊗vΦ(λ1,0)+a3δλ2=1∂1∂2⊗vΦ(λ1,1),

0=∂2·y=a1δλ2=0∂2⊗vΦ(λ1,0)-a2δλ2=1∂1∂2⊗vΦ(λ1,-1),

于是a1δλ2=0∂1⊗vΦ(λ1,0)=a1δλ2=0∂2⊗vΦ(λ1,0)=a2δλ2=1∂1∂2⊗vΦ(λ1,-1)=a3δλ2=1∂1∂2⊗vΦ(λ1,1)=0.

这意味着a1δλ2=01⊗vΦ(λ1,0)=a2δλ2=1∂1⊗vΦ(λ1,-1)=a3δλ2=1∂2⊗vΦ(λ1,1)=0.进而y=a4δλ2=2∂1∂2⊗vΦ(λ1,0).

由于vΦ(λ1,0)≠0⟺0≤Φ(λ1,0)≤Φ(λ1),于是下面对Φ(λ1,0)和Φ(λ1)的大小关系分2类进行讨论.

i) 当Φ(λ1,0)<Φ(λ1)时，注意到

0=x2∂1·y=a4δλ2=2∂1∂2⊗vΦ(λ1,2).

由于Φ(λ1,2)=Φ(λ1,0)+1≤Φ(λ1)，所以∂1∂2⊗vΦ(λ1,2)≠0.进而a4δλ2=2=0，即y=0.

ii)当Φ(λ1,0)=Φ(λ1)时，即λ1=0，亦即y=a4δλ1=0δλ2=2∂1∂2⊗v0.容易证明当λ1=0，λ2=2时，∂1∂2⊗v0∈H0(W(2),KS(λ)).

于是当S=0且λ=(0,2)时，H0(W(2),KS(λ))是一维的，具有基∂1∂2⊗v0；当S=0但λ≠(0,2)时，H0(W(2),KS(λ))是零维的.

2)设S正则幂零且r=0.任取y∈H0(W(2),KS(λ)),不妨设

y=a1δλ2=01⊗vΦ(λ1,0)+a2δλ2=1∂1⊗vΦ(λ1,-1)+a3δλ2=1∂2⊗vΦ(λ1,1)+a4δλ2=2∂1∂2⊗vΦ(λ1,0)，

故∂1·y=∂2·y=x2∂1·y=0，即

a1δλ2=0∂1⊗vΦ(λ1,0)+a3δλ2=1∂1∂2⊗vΦ(λ1,1)=0,

a1δλ2=0∂2⊗vΦ(λ1,0)-a2δλ2=1∂1∂2⊗vΦ(λ1,-1)=0,

a2δλ2=1∂1⊗vΦ(λ1,1)+a3δλ2=1(-∂1⊗vΦ(λ1,1)+∂2⊗vΦ(λ1,3))+a4δλ2=2∂1∂2⊗vΦ(λ1,2)=0.

进而

a1δλ2=0=a2δλ2=1=a3δλ2=1=a4δλ2=2=0,

即y=0.