李超三系的形心及其性质

赵冠华，朱玉龙，刘 洁

由于李超三系在数学和物理上的一些应用，特别是可以用于求解Yang－Baxter方程，从而引起了人们的研究兴趣［1－5］.形心的概念在研究代数的结构和分类中起着重要的作用［6－14］，受此启发，论文将讨论李超三系的形心及其性质.首先回顾一些基本概念，未提到的有关概念请分别参阅文献［4，14］.

设V=V0⊕V1是Z2－阶化线性空间，其中:V0={x∈V|d(x)=0}，V1={x∈V|d(x)=1}，d(x)表示x的阶化次数.简记(－1)d(x)d(y)=(－1)x·y.总假定文中的元素是齐次的，即或者x∈V0，或者x∈V1.

定义1 一个Z2－阶化线性空间T=T0⊕T1，如果它有三元线性运算满足

1)d(［x，y，z］)=d(x)+d(y)+d(z)(mod 2);

2)［x，y，z］ = － (－ 1)xy［y，x，z］;

3)(－ 1)xz［x，y，z］+(－ 1)yx［y，z，x］+(－ 1)zx［z，x，y］ =0;

4)［u，v，［x，y，z］］= ［［u，v，x］，y，z］+(－ 1)(u+v)x［x，［u，v，y］，z］+(－ 1)(u+v)(x+y)［x，y，［u，v，z］］.则称 T 为一个李超三系.

设T=T0⊕T1是一个李超三系，L是T的Z2－阶化子空间，若［L，T，T］⊆L，称L是T的理想.若I，J分别是李超三系T的理想，则I+J，I∩J都是T的理想.令Z(T)={x∈T|［x，T，T］=0}，称Z(T)是T的中心，显然Z(T)是T的理想.

规定李超三系T的左乘和右乘变换分别为

L(x，y):L(x，y)(z)= ［x，y，z］;R(x，y):R(x，y)(z)=(－ 1)z·(x+y)［z，x，y］，∀x，y，z∈ T.

显然d(L(x，y))=d(x)+d(y)，d(R(x，y))=d(x)+d(y)(mod 2).若李超三系T的所有左乘变换的集合记为 H=L(T，T)={∑L(xi，yj)|xi，yj∈ T}，可得到 H 构成一个李超代数［4］.

设 T=T0⊕ T1是一个李超三系，令 EndαT={φ ∈ End T| φTs⊆ Ts+α，s=0，1}，α =0，1.则结合超代数End T=End0T⊕End1T，按照运算［a，b］=ab－(－1)abba构成李超代数.

定义2 设T是一个李超三系.称Γ(T)={φ∈End T|［φ，L(x，y)］=［R(x，y)，φ］=0}为李超三系T的形心.

定义3 设T是一个李超三系.在空间直和L(T)=T⊕H中规定二元运算，满足

［t1⊕h1，t2⊕h2］=(h1(t2)－ (－ 1)h2·t1h2(t1))⊕(L(t1，t2)+［h1，h2］)，∀t1，t2∈T，h1，h2∈H.则称L(T)为李超三系T的标准嵌入李超代数.

定理1 设T为一个李超三系，则

证明 由 Γ(T)={φ ∈ End T|［φ，L(x，y)］ = ［R(x，y)，φ］ =0}，可得

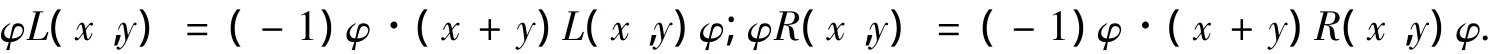
对任意 x，y，z∈ T，有

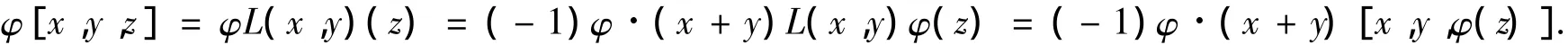
又由 φR(x，y)(z)=(－ 1)φ·(x+y)R(x，y)φ(z)，(－ 1)φ(x)=(－ 1)φ +x，可得

定理2 设T为一个李超三系.则Γ(T)是一个可换的李超代数.

证明 对任意 φ，φ ∈ Γ(T)，x，y，z∈ T，有

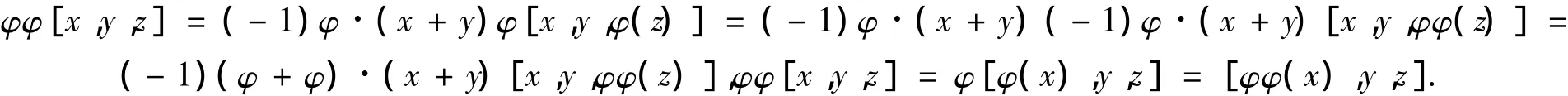
由定理 1可知 φφ ∈ Γ(T)，即 Γ(T)是一个结合超代数.规定二元运算［φ，φ］ =φφ －(－1)φ·φφφ，易证Γ(T)可以构成一个李超代数.

又由 φφ［x，y，z］ = φ［φ(x)，y，z］ =(－ 1)φ·(φ(x)+y)［φ(x)，y，φ(z)］，有

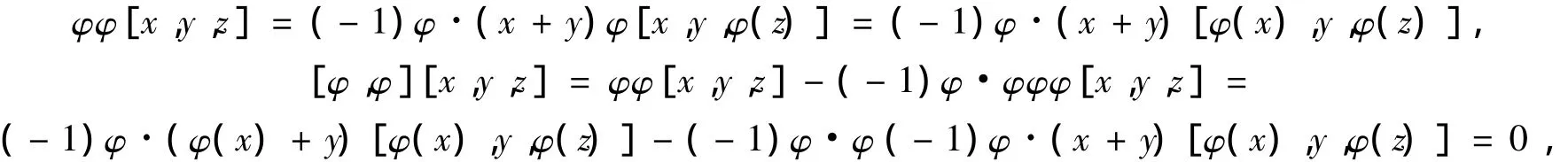
即［φ，φ］=0，所以Γ(T)是一个可换的李超代数.

定理3 设T为一个单李超三系.则Γ(T)具有可除性.

证明 由于T的理想在H作用下是不变的，T为单李超三系当且仅当H是不可约超代数.

对任意 φ ∈ Γ(T)，φ ≠0，x，y∈ T，有

可得φ(T)在H作用下是不变的，即φ(T)=T.从而φ是一个满射.又由T为单李超三系，可得kerφ =0.从而φ是一个单射.所以φ是一个双射，即φ－1∈End T.

对任意 x，y，z∈ T，有

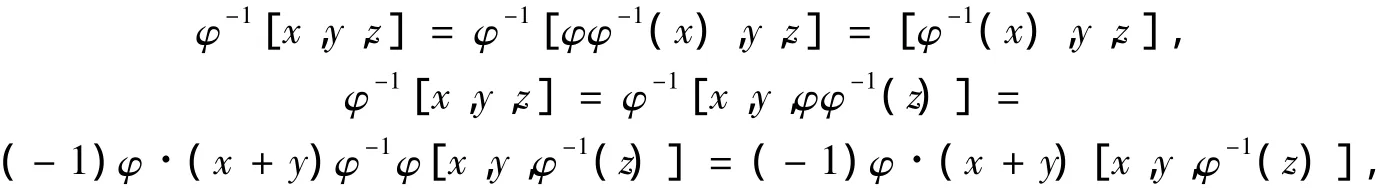
从而φ－1∈Γ(T)，即Γ(T)具有可除性.

定理4 设T为一个李超三系，L(T)=T⊕H为其标准嵌入李超代数.则对任意φ∈Γ(T)，存在ψ ∈Γ(L)，使得 ψ|T= φ，ψ|H∈ Γ(H).

证明 对任意φ∈Γ(T)，t⊕h∈L(T).规定L(T)上的变换:

任取 h∈ H，由［φ，h］ =0，故有 φh=(－1)φ·hhφ.对任意 h∈ H，可得

对任意 t1，t2，z∈ T，可得

即对任意t1⊕h1，t2⊕h2∈L(T)，可得

所以 ψ ∈ Γ(L).显然 φ|T= φ，又由 φh=(－1)φ·hhφ，可得 φ|H∈Γ(H).

设L(T)为李超三系T的标准嵌入李超代数.规定L(T)的自同构

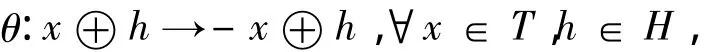
则称θ为L(T)的主对合自同构.

引理［4］设L(T)为李超三系T的标准嵌入李超代数.则对∀x，y，z∈T，有

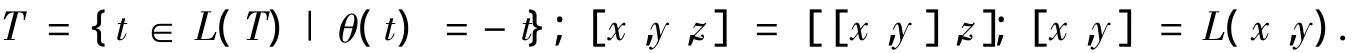
定理5 设T为一个李超三系，L(T)=T⊕H为其标准嵌入李超代数.若对任意ψ∈Γ(L)，且ψθ= θψ.则有 ψ |T∈ Γ(T).

证明 任取t∈T，由于

可得ψ(t)∈T，即ψ|T∈End T.

对任意 x，y，z∈ T，有

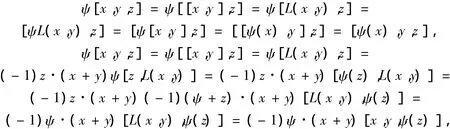
所以

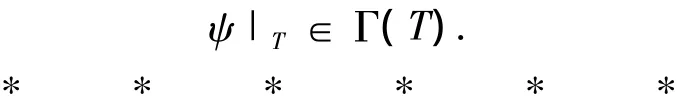
致谢:在写作过程中得到了河北大学张知学教授的指导和帮助，在此深表谢意.

［1］ Okubo S，Kamiya N.Quasiclassical Lie superalgebras and Lie supertriple systems［J］.Comm Alg，2002，8:3825 －3850.

［2］ Okubo S，Kamiya N.Jordan－ Lie superalgebras and Jordan － Lie supertriple systems［J］.J Alg，1997，198:388 －411.

［3］ Okubo S.Triple products and Yang － Baxter equation and symplectic ternary systems［J］.J Math Phys，1993，34:3273－3292.

［4］ Zhang Z X，Jia P P.The killing forms and decomposition theorems of Lie supertriple systems［J］.Acta Math Scientia，2009，29B:1 －11.

［5］ 潘玉霞，张庆成.李超三系的分解唯一性［J］.数学物理学报，2008，28A:1058－1066.

［6］ Jocabson N.Lie and Jordan triple systems［J］.Amer JMath，1948，71:148 －170.

［8］ Hophins N.On the derivation algebra of Lie module triple systems［J］.J Algebra，1987，111:520 －527.

［9］ Lister W G.A struction theory of Lie triple systems［J］.Trans Amer Math Soc，1952，72:217 －242.

［10］ Hophins N.Nilpotent ideals in Lie and anti-Lie triple systems［J］.JAlgebra，1995，178:480 － 494.

［11］ Shi Y Q，Meng D J.On derivations and automorphism group of Lie triple systems［J］.JNankai University，2002，35:32－37.

［12］ 张知学.反李三系的不变双线性型［J］.数学年刊，2004，25A(4):429－436.

［13］ 孟道骥.复半单李代数引论［M］.北京:北京大学出版社，1998.

［14］ 张知学，刘丽巧.李超代数上的不变双线性型［J］.数学年刊，2004，25A:1139－1146.