基于RELM的时间序列数据加权集成分类方法*

赵林锁，陈 泽，丁琳琳，宋宝燕

(1.辽宁工程技术大学力学与工程学院,辽宁 阜新 123000;2.辽宁大学信息学院,辽宁 沈阳 110036)

1 引言

时间序列数据通常是指一系列带有时间间隔的实值型数据[1]。它的特点是不同时刻数据之间存在着某种关联，这种特性反映了数据在随着时间变化的过程中存在着某种规律[2]。时间序列数据广泛应用于灾害监测[3]、金融监管[4]和医疗[5]等领域。时间序列数据之间的类别差异具体体现在其数据的传播频率不同、数据幅值大小差别以及数据点间的时间间隔不同等方面。例如，对于矿山监测领域所产生的时间序列数据来说，微震监测系统中的传感器接收到微震波，均会产生微震时间序列数据，由于其传播速度不同，产生的幅值大小不同，导致每次发生的微震事件类型不同，造成的危害程度也不同，后期救援的方式方法亦不同[6]；对于医疗领域的心电时间序列数据来说，医疗心电信号也是一种时间序列数据，医生会依据心电信号的频率大小和幅值高低来区分心电信号的类别，根据不同类型的心电信号给出不同的诊治方案[7]。因此，有效分类时间序列数据具有极其重要的意义。

然而，现实应用中的时间序列数据常常伴有大量的环境噪声[8]。例如，矿山微震时间序列数据中，由于矿区环境复杂，传感器产生的时间序列数据常常伴有大型机械作业、水流等环境噪声；心电时间序列数据中，大量患者的心电时间序列数据通常会受到外来环境因素干扰，产生环境背景噪声。噪声引起对应的时间序列数据出现偏差，极大地改变了时间序列数据的真实形态，在一定程度上影响了时间序列数据的分类精度。因此，在对此类时间序列数据分类之前，需要对时间序列数据进行降噪预处理。

由于时间序列数据通常具有维度高、数据量较大的特性，许多学者对其分类方法进行了深入研究。Luo等[9]提出了一种基于SVM(Support Vector Machine)的重构训练集RTS-SVM(Reconstructed Train Set-Support Vector Machine)方法来实现时间序列数据分类，并采用了轮盘赌协同进化算法R-CC(Roulette Cooperative Coevolution)优化RTS-SVM的参数。但是，该方法没有充分考虑到关键支持向量，分类性能仍有待提升。Yang等[10]提出了一种卷积神经网络CNN(Convolutional Neural Network)和递归神经网络RNN(Recurrent Neural Network)相结合的分类方法DPCRCN(Dual Path CNN RNN Cascade Network)，首先利用CNN进行数据特征提取，再使用RNN学习特征和输出映射，但其中的数据融合方法仍然存在问题，且训练模型时间较长。Li等[11]提出了一种基于极限学习机ELM(Extreme Learning Machine)和自适应集成技术的时间序列预测方法，并在大量的时间序列数据集上进行了验证，算法的泛化性能还有待提升。综上，使用机器学习算法对时间序列数据分类还存在着预测精度较低、泛化性能较差的缺陷。

本文以正则化极限学习机RELM(Regularized Extreme Learning Machine)作为基分类器，提出了一种基于RELM的时间序列数据加权集成分类方法E-PSO-RELM(Ensemble-Particle Swarm Optimization-Regularized Extreme Learning Machine)。在数据挖掘领域的UCR时间序列数据开源数据集[12]上进行了仿真实验，实验结果表明，相比于其他方法，本文方法能够有效提高时间序列数据的预测精度且提升了泛化性能。本文主要贡献如下所示：

(1)针对时间序列数据中所含有的噪声，引入了小波包变换WPT(Wavelet Packet Transform)方法，基于其较高的时间序列数据时频分辨率，通过阈值函数处理小波包系数，进而去除噪声。即将时间序列数据通过WPT方法分解成小波包系数，并对小波包系数进行阈值量化处理，再对其重构得到去噪后的时间序列数据。

(2)针对去噪后的时间序列数据分类，本文提出了一种有效选取RELM基分类器的方法。通过训练RELM的隐藏层节点的数量，计算得到不同隐藏层节点数量下的预测标签，并选出分类精度最高的隐藏层节点数量所对应的RELM作为基分类器。

(3)针对时间序列数据维度高、数据量较大，导致单个基分类器的预测精度较低、泛化性能较差的问题，本文提出了一种基于粒子群优化PSO(Particle Swarm Optimization)算法的RELM基分类器权值优化方法。考虑到PSO算法结构简单、迭代速度快的特点，同时考虑到各个RELM基分类器之间的信息互补性，通过PSO算法不断优化基分类器的权值，对时间序列数据进行加权集成分类。

2 相关工作

近年来，许多学者对时间序列数据进行了广泛深入的研究[13]。在时间序列数据分类的问题中，极限学习机(ELM)作为一种单隐层前馈神经网络机器学习算法，其具有算法结构简单、泛化性能好的特点，往往只需设置隐藏层节点的数量即可求得最优唯一解[14]，ELM凭借这些特点被广泛地应用在关于时间序列数据的处理问题中[15,16]。Yan等[17]提出了一种基于卡尔曼滤波器与ELM相结合的方法CS-DELM(Cost Sensitive-Dissimilar ELM)对时间序列数据进行了分类研究，但该方法在处理时间序列数据时仍然存在不稳定性，泛化性能有待提升。Xu等[18]提出了一种基于MOPSO-ELM(Multi Objectives Particle Swarm Optimization-ELM)的分类方法，利用改进的粒子群优化算法(PSO)对ELM的参数进行了优化，提高了预测精度，但算法的复杂度较高，训练时间较长。Fan等[19]提出了一种基于极限学习机(ELM)的改进分层集成结构EILEA(ELM-Improved Layered Ensemble Architecture)对时间序列数据进行了预测，该方法提升了平均预测精度和运行效率，但没有对ELM的隐藏层节点数量进行优化，泛化性能较差。

综上，在使用单分类器对时间序列数据进行分类时会出现分类结果不稳定、泛化性能较差的问题。集成分类方法往往能够有效解决这一问题。集成分类方法通常按照某种规则对性能较差的弱分类器进行组合，能够有效提高分类性能[20]。但是，在实际应用中，若所需的基分类器数量较少或是重用常见分类器的一些经验时，研究者往往会选择具有一定分类性能的强分类器作为基分类器来提升分类性能，并且通过对分类器的权值进行优化，能够充分利用分类器间的信息互补性，并给每个基分类器赋予不同权值来弥补分类器之间的差异。Liu等[21]提出了一种基于ELM的加权集成分类方法，针对数据的不平衡现象，结合样本的分布引入了平衡因子，并通过加权集成方法提升了方法的稳定性。Feng等[22]提出了一种基于马尔科夫链的动态加权集成信用评分方法，根据每个基分类器分类性能的变化，调整基分类器的权重，并验证了方法的预测精度和效率。

在集成分类方法中的基分类器选择方面，传统的ELM分类方法中的输出权值矩阵是由隐含层矩阵的广义逆所得出的，导致传统的ELM分类方法仍然存在过拟合现象，降低了分类精度和泛化性能；针对ELM的这种缺陷,RELM通过引入正则化因子，并同时考虑了经验风险和结构风险，构建了新的目标函数；相对于ELM能够有效地提高分类精度和泛化性能[23]。

因此，本文针对现有时间序列数据分类方法的不足，为提高分类方法的预测精度、泛化性能，以及考虑到集成分类方法的良好特性，以RELM作为基分类器，提出了一种基于RELM的时间序列数据加权集成分类方法。

3 时间序列数据去噪

时间序列数据常常伴有大量的环境噪声，降低了分类精度，影响了时间序列数据的后续处理，因此对时间序列数据进行去噪是非常必要的。考虑到小波包方法的多频率分析特性，本文使用基于小波包的去噪方法，通过对时间序列数据的频带多尺度划分获取小波包系数，然后对高频和低频小波包系数进行阈值量化处理，并通过对小波包系数重构，得到去噪后的时间序列数据。

3.1 小波包系数的获取

小波包系数的获取是指对时间序列数据逐层分解，并将分解后得到的小波包系数进行阈值量化处理，以优化小波包系数，从而达到去噪效果的过程。图1所示为对带有环境噪声的时间序列数据X(t)进行3层小波包系数分解，其中P[i,j]表示分解得到的小波包系数。

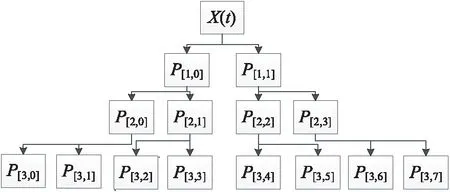
Figure 1 Wavelet packet coefficient decomposition

在图1所示的小波包分解过程中，首先对时间序列数据X(t)分解为第1层小波包系数P[1,0]和P[1,1]，分解公式如式(1)所示：

(1)

其中，将原始时间序列数据X(t)分别通过低通滤波器h和高通滤波器g(其中k,l表示滤波器系数,z表示分解总层数)分解为第1层小波包系数P[1,0]和P[1,1]，P[1,0]表示低频小波包系数，P[1,1]表示高频小波包系数。并且在接下来的每一次分解过程中均会将每一组小波系数P[i,j]分解成2个频率子带的小波包系数，得到低频小波包系数P[i+1,2j]与高频小波包系数P[i+1,2j+1]，每组小波包系数分解公式如式(2)所示：

(2)

其中P[i,j]表示第i层第j组小波包系数。

经过小波包分解后，时间序列数据与小波包的系数关系也可近似表示为式(3)所示：

X(t)=P[1,0]+P[1,1]=

P[2,0]+P[2,1]+P[2,2]+P[2,3]=

P[3,0]+P[3,1]+P[3,2]+P[3,3]+

P[3,4]+P[3,5]+P[3,6]+P[3,7]

(3)

接下来，根据软阈值函数处理原则[24]，对最后一层的每组小波包系数P[i,j]={P[i,j](1),P[i,j](2),…,P[i,j](n)}进行阈值量化处理，n表示小波包系数的个数，阈值处理函数如式(4)所示：

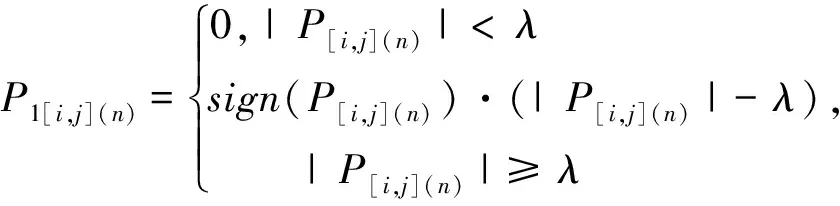
(4)

其中,λ表示设定的阈值，P[i,j](n)表示需要被优化的小波包系数，P1[i,j](n)表示优化后的小波包系数，sign(·)表示阶跃函数。

3.2 小波包系数的重构

小波包系数的重构是指对最后一层使用阈值函数处理后的小波包系数逐层重构得到去噪后的时间序列数据的过程，小波包系数重构的过程如图2所示，其中Y(t)表示去噪后的时间序列数据，P1[i,j]表示优化后的小波包系数。

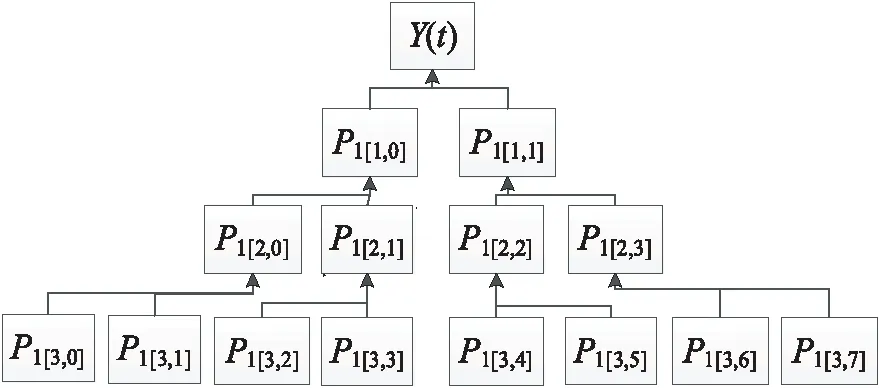
Figure 2 Reconstruction of wavelet packet coefficient

在每一层中的小波包系数重构公式如式(5)所示:

(5)

其中,h和g分别表示为低通滤波器和高通滤波器。最后由第1层小波包系数重构得到时间序列数据Y(t)。

在本节中经过小波包去噪后所得到的时间序列数据Y(t)，再通过下一节的加权集成分类方法进行分类。

4 时间序列数据的加权集成分类

针对去噪后的时间序列数据，本文提出了一种训练RELM隐藏层节点数量的方法，可有效选取基分类器。针对时间序列数据的数据量较大、数据维度较高的特点，以及在实际应用中使用单个基分类器分类时较易出现不稳定性，导致分类器预测精度不高、泛化性能较差的缺陷，本文提出了一种基于PSO算法的RELM基分类器权值优化方法，结合PSO算法的特点，通过PSO对基分类器进行权值优化，实现对时间序列数据的加权集成分类。

4.1 基分类器选取

RELM是一种结构简单、计算迅速的单隐层前馈神经网络学习算法。在集成分类方法中，不同的隐藏层节点数量对应着不同性能的RELM基分类器。首先计算各个基分类器的预测标签，再选取较高分类精度所对应的隐藏层节点数量，从而确定RELM基分类器。

(1)预测标签的计算。

针对去噪后的时间序列数据，初始化多个RELM基分类器，并以去噪后的时间序列数据作为输入，来计算RELM基分类器的预测标签。

其过程可表述为将去噪后的时间序列数据输入到各个初始化的RELM中，并以RELM的隐藏层节点数量为循环条件，计算每个隐藏层节点数量下的预测集标签。具体过程为：假设去噪后的时间序列数据为Y={y1,y2,…,yk}，数据的类别标签为T={1,2,…,a}，其中a表示标签个数，首先将数据分为训练集数据Y1和预测集数据Y2，以RELM的隐藏层节点数量J做为循环条件，将训练集数据Y1输入到RELM，并计算当前隐藏层节点数量为J时的输出权值矩阵LW，将预测集数据Y2输入到RELM中，通过LW得到当前隐藏层节点数量下的预测集标签T′(J)。

(2)隐藏层节点数量的获取。

得到预测集标签后，计算不同隐藏层节点数量下的分类精度，选取分类精度较高时的隐藏层节点数量，作为所需的RELM基分类器的隐藏层节点数量。

其具体过程为：通过(1)中所得到的预测集标签T′(J)，根据预测标签的结果计算当隐藏层节点数量为J时的分类精度acc(J)，并将acc(J)存储到列表S中。再根据acc(J)选取集成分类方法中的分类器。其具体做法为:令集成分类中的基分类器个数为q，随着隐藏层节点数量J的不断增加，分类精度会趋于稳定，但过多的隐藏层节点数量会使运行效率变低，则需计算q个分类精度的平均值。由于在训练初期，精度平均值相对较低，而随着隐藏层节点数量J的增加，其平均值也会逐渐变大，为了避免隐藏层节点数量J较大，则需在平均值处于相对较高且趋于稳定的初期时，获取其对应的隐藏层节点数量值，从而能够得到对应的基分类器数量。其中，为了有效识别平均值何时保持稳定，在训练过程中设定阈值λ，若在相邻w个精度平均值中任意2个值均小于或等于λ，则选取当前条件下的第1个平均值所对应的隐藏层节点数量J。

(3)算法描述。

确定了隐藏层节点数量J，也就是确定了所需的RELM基分类器。RELM基分类器选取方法如算法1所示。输入去噪后的时间序列数据Y，通过训练隐藏层节点数量J的方法得到预测集标签;然后根据预测标签计算隐藏层节点数量J所对应的分类精度acc(J)，并通过acc(J)来选取所需的基分类器。其中，g表示调谐参数，G(·)表示激活函数。

算法1基分类器选取方法

Input:数据集Y={y1,y2,…,yk},数据类别T={1,2,…,a},隐藏层节点数量取值范围为[m,v],c为步长。/*m表示初始值,v表示最大值*/

Output:隐藏层节点数量J和对应分类精度acc(J)。

Initialization:训练集数据被随机分为2组向量,命名为Y1 和Y2；创建S列表,SJ存储J及其对应的分类精度acc(J)。

//获得预测数据标签T′(J)

1forJ=mtovdo

2IW,B←Y1;

3H=G(IW*Y1+B);

4LW=(H′H+gI)H′Y1;

5IW1,B1←Y2;

6H1=G(IW1*Y2+B1);

7T′(J)←Softmax((H′1*LW)′);

8endfor

//计算分类精度

9forJ=m:c:vdo

10sum=0;

11while(T(J)=T′(J)):

12sum++;

13endwhile

14v=T(J).length;

15acc(J)=sum/n;

16S←J,acc(J);

17endfor

//选取多个基分类器

18t=1;

19whilet≤5:

/*计算相邻5个基分类器的分类精度平均值avg_acc*/

20ifavg_acc≤λ

21t=t+1;

22elseJ=J+50;

23endwhile

在时间复杂度方面，算法1由3个循环组成，其平均时间复杂度为O(n)，最好和最坏情况下的时间复杂度也为O(n)。在空间复杂度方面，算法1的存储空间会随着RELM的隐藏层节点数量的变化而变化，因此空间复杂度为S(n)。

4.2 基于PSO的基分类器权值优化

在得到RELM基分类器后，为每个基分类器赋予初始权值，再通过PSO算法不断优化基分类器的权值，对时间序列数据进行加权集成分类。

(1)基分类器的权值优化。

针对时间序列数据维度高、数据量较大的特性，在使用单个分类器分类时仍然存在预测精度低、泛化性能较差的问题，并考虑到PSO的特点以及各个RELM基分类器之间的信息互补性，本节给出了一种基于PSO的基分类器权值优化方法。

其具体过程为：以基分类器的权值作为PSO的粒子，以预测精度作为PSO的适应度函数值，随着迭代次数的增加不断优化基分类器的权值。假设输入样本集数据Y，初始化种群规模为K，即共有K个粒子Xi和粒子速度Vi,其中,Xi=[xi1,xi2,…,xin],Vi=[vi1,vi2,…,vin],i∈{1,2,…,K},xij存储的值为第i个粒子的第j个基分类器的权值aj，Vi是元素值为[0,1]的随机矩阵。对每次迭代中的每个粒子计算其预测结果T；并求出每个粒子的适应度函数值，即分类精度acc={acc(1),acc(2),…,acc(t),…,acc(K)}，其中acc(i)表示第i个粒子的适应度函数值。根据所有粒子的适应度函数值，得到每个粒子Xi的全局最优值gbesti和每个粒子的个体最优值pbesti，其中i∈{1,2,…,K}。通过PSO的粒子更新公式来优化每个粒子的下一次迭代的粒子和速度。随着迭代次数的增加，当迭代次数达到最大值时，得到最优基分类器权值a。

(2)加权集成分类。

得到基分类器优化的权值后，接下来对时间序列数据进行加权集成分类：

通过上一节中所得到的每个分类器的权值ai，则每个样本Xk被分到j类中的概率值为xjk，计算公式如式(6)所示:

(6)

其中,yji表示第i个分类器将样本分类到j类的概率值，n表示分类器个数。

再根据加权分类器的加权投票方法选出最大值所对应的类别作为Xk的预测分类结果j，如式(7)所示。

Xjk=max{x1k,x2k,x3k,…,xmk}

(7)

(3)方法描述。

优化了基分类器的权值后，对时间序列数据进行加权集成分类，算法2为本文提出的基于RELM的加权集成分类方法(E-PSO-RELM)。其中将分类器的权值作为PSO算法的粒子，通过式(6)和式(7)来计算每次迭代过程中的预测结果，并计算出预测精度作为PSO的适应度函数值，通过迭代次数的增加来优化基分类器的权值，得到优化的权值后再对数据集进行集成分类。

算法2基于RELM的加权集成分类方法(E-PSO-RELM)

Input:数据集Y,分类器个数n,迭代次数最大值Tmax; PSO相关参数：惯性权重ω,学习因子c1,c2,种群数量K。

Output:基分类器的权值(a1,a2,a3,…，an)。

Initialization:随机初始化K个粒子Xi=[xi1,xi2,…,xin],i∈{1,2,…,K};n表示分类器的数量;xij表示第j个 基分类器的权重ai,和K个种群规模的粒子速度值Vi=[vi1,vi2,…,vin],i∈{1,2,…,K}。

1whilet≤Tmaxdo:

//计算预测结果acc=[acc1,acc2,…,accK];

2fori=1 toKdo:

3fora=1 tomdo:

5T′(a)←argmax{x1i,x2i,x3i,…,xmi};

6endfor

7acc(i)←(ACC{T(i)′-T(i)};

8gbesti,pbesti←Find(acc);

11endfor

12t=t+1;

13endwhile

在该算法中，根据设定的PSO种群规模K值和设定的分类器数量n，其平均时间复杂度为O(nK)；并且由于算法2没有额外的存储空间开销，其空间复杂度为S(1)。

5 实验评估

为了验证本文方法的有效性，将其与目前常用的3种分类方法进行了对比。实验的硬件配置为Windows 10系统主机、16 GB内存、Intel(R)Core i5-9300H CPU 2.40 GHz以及64位操作系统。分类算法均在Matlab 2018a上实现。

5.1 数据集介绍

本文实验所选取的所有数据来自于时间序列挖掘领域的开源数据集资源UCR时间序列数据集[12]。由于UCR中数据集的数量较多，且数据集的数据维度具有较大差异，因此本文根据UCR数据集的数据特征，选取了具有代表性的16组数据集作为实验数据集。实验中所用到的数据集的具体信息如表1所示。

Table 1 Introduction of data sets

5.2 实验结果与分析

(1)基分类器选取实验。

选择5个RELM基分类器对本文集成分类方法进行集成分类实验。在本节中，通过本文提出的训练隐藏层节点数量的方法来确定每个数据集的RELM分类器数量；针对数据维度的不同，将16个数据集分为2组进行对比实验。

图3所示为训练RELM隐藏层节点数量实验结果，其中由于部分数据集的数据维度较高，所选取的隐藏层节点数量区间，即算法1中的[m,v]，取值为[100,2000]，如图3b表示；其他数据集的隐藏层节点数量区间选择为[100,1200]，如图3a表示。由于隐藏层节点数量相近时，通常得到的精度差别较小，因此，在实验中，以50为步长依次选取隐藏层节点数，这里的50为经验值，同时为算法1中的c值。

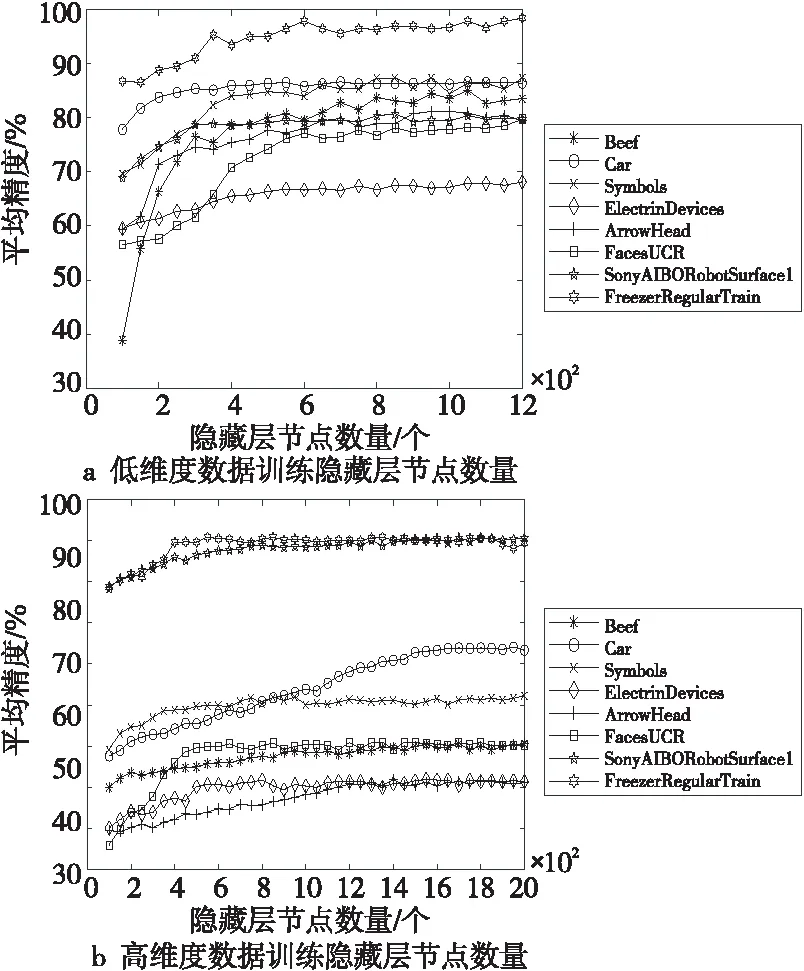
Figure 3 Number of hidden layer nodes in training RELM

在进行加权集成分类实验之前，先通过4.1节中提出的方法进行了训练隐藏层节点数量实验来确定每个数据集的基分类器数量；每个数据集上分别进行了20次实验，选取平均分类精度作为实验的评价标准。从图3中可以看出，不同的样本的平均分类精度以及所选取的隐藏层节点数量是不同的，并且平均精度的值在初始阶段均处于上升趋势，但数据集的维度和大小不同，得到的精度值大小也有差异，最终均会处于一个相对稳定的状态。根据4.1节中的方法，在保证分类精度相对稳定时即开始选取隐藏层节点数量，为能够有效地选取隐藏层节点数量，令算法1中的阈值λ取值为[0.35，0.5]，即选取多个平均分类精度差值在[0.35，0.5]内的值，并将该值对应的隐藏层节点数作为实验所需的隐藏层节点数，此区间值为本次实验的经验值。根据图3中的信息，对数据集的基分类器进行了选取，每个数据集选取的基分类器所对应的隐藏层节点数量信息如表2所示。

Table 2 Classifier selection

(2)加权集成分类实验。

在通过上述方法得到5个基分类器后，为了确保分类器之间具有一定的区分性，为每个分类器均赋予不同的激活函数sig(x)，目前被广泛使用的激活函数有sigmoid函数、ReLU(Rectified Linear Units)函数、Swish函数、sin函数和RBF(Radial Basis Function)函数[13]。

为了更好地验证本文方法的分类性能，选取ELM、E-ELM(Ensemble-ELM)、Vote-ELM、MGEoT(Multi Granularity Ensemble classification method)[25]、PCA-LSTM(Principal Component Analysis-Long Short Time Memory)[26]5种方法进行对比实验，各方法的具体介绍如表3所示。

在进行实验之前，首先对时间序列数据进行WPT去噪处理，然后每次实验均进行20次，取平均预测精度作为评价标准；并对本文提出方法中的PSO参数进行初始化，PSO的迭代次数为200次，学习因子c1和c2分别为0.8和0.2，惯性权重ω为0.5。并将本文提出的方法中的基分类器的初始权值ai均设为1。

Table 3 Introduction to classification methods

方法的泛化性能是指通过训练样本数据训练出来的模型，不仅能够对原有的训练集数据进行准确的分类，同样能够对预测集数据进行准确分类。为验证本文方法的泛化性能，本文选取预测集数据分类结果的平均分类精度作为评价标准。图4所示为不同分类方法对预测集数据分类结果的平均分类精度比较。

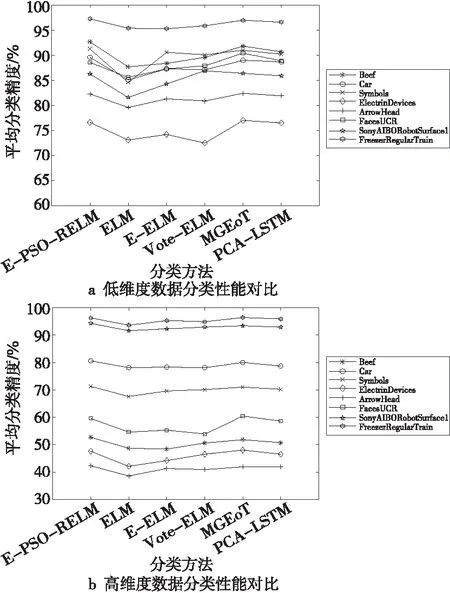
Figure 4 Comparison of average classification accuracy of methods

从图4中可发现，对比单个分类器，集成分类方法均有较好的效果。从图4a中可发现，在Symbols和SonyAIBORobotSurface1这2个低维度数据集上，由于训练集和测试集的数据个数差别较大，在单个分类器分类时由于训练数据较少不能够较好地得到训练模型，导致分类精度较低，泛化性能较差，而通过实验表明，集成分类方法较好地弥补了这一缺陷。在实验结果中，利用不同的分类方法处理不同的数据集所得到的分类结果均不同，对于低维度的数据集，集成分类的优化效果相比于其他4种高维度数据不够明显，这体现了集成分类能够很好地弥补分类器在处理高维度数据时所存在的差异性。通过图4也能发现，本文提出的对权值优化的E-PSO-RELM相比其他2种不对权值优化的方法E-ELM和Vote-ELM的分类性能均要好一些，并且具有与MGEoT和PCA-LSTM这2种方法相近的分类性能。并且从图4b中可发现，在MixedShapeSmallTrain和StarLightCurves这3个数据集上，对比于其他高维度数据集，本文方法得到的分类结果均较良好，这是由于虽然这2个数据集的维度较高，但在保证数据集个数一定多的条件下，也有助于提升分类性能。因此，在今后的实验中可以通过不断增加数据集的个数来检测分类器的性能。从图4中还能发现，对于维度最高的InlineSkate数据集，在使用单个ELM分类器分类时，由于单个分类器往往存在不稳定性，导致每次得到的预测精度大小差别较大，因此所求得的平均值较低。本文提出的E-PSO-RELM加权集成方法，对分类器赋予不同的权值，有效地改善了这种缺陷，同时也较好地提升了分类器的分类性能。然而，由于PSO属于一个迭代过程，在训练及分类过程中均需要一定的时间进行迭代，相比于其他2种方法在运行效率方面仍有一定的缺陷。

6 结束语

时间序列数据有效分类在人们日常生活中变得越来越重要。针对时间序列数据中通常伴有大量环境噪声的问题，本文结合小波包去噪方法的优势，通过阈值量化处理小波包系数，有效地去除了噪声。针对时间序列数据维度高、数据量较大的特性，本文提出的基于RELM的时间序列数据加权集成分类方法，充分利用了PSO算法的优势以及各个RELM基分类器之间的信息互补性，实现了对时间序列数据的有效分类。在仿真实验中，将本文方法与目前典型的时间序列分类方法进行了性能对比，结果表明：本文所提出的分类方法优于其他3种对比方法，通过有效提高分类的预测精度和泛化性能，进而有效提升了对时间序列数据的分类性能。