也谈符号意识及其培养

摘要：作为数学课程要培养的学生核心素养的主要表现之一，符号意识是把符号视为重要的语言，理解符号的意义，体会符号的特点，并根据非符号表征的情境创造符号和使用符号，因而表现为符号理解、符号表示、符号操作三个方面。根据这三个方面表现的关系，在小学数学教学中，教师可以重点引导学生创造数学符号表示意义，操作数学符号发展意义，并在这一过程中充分理解数学符号的意义，体会（感悟）数学符号的特点（功能），从而培养学生的符号意识。

关键词：小学数学；符号意识；符号表征；符号操作

一、 符号意识的表现

符号意識是《义务教育数学课程标准（2022年版）》（以下简称“新课标”）提出的数学课程要培养的学生核心素养的主要表现之一。仔细分析新课标对符号意识的描述可以发现，其主要表现为三个方面。首先，“知道符号表达的现实意义”“知道用符号表达的运算规律和推理结论具有一般性”（③④ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：8，8，8。），这指向“符号理解”。它要求学生能够认识常见的数学符号（如数字符号、字母符号、运算符号、关系符号、表示图形的符号以及具有特定意义的辅助符号等），理解它们在具体情境中表示的意义，体会它们所具有的准确性、简约性、抽象性、一般性等特点（邵光华，张妍，程玉婷.再谈数学语言及数学语言能力培养［J］.教育研究与评论，2022（7）：54。）。其次，“能够初步运用符号表示数量、关系和一般规律”③，这指向“符号表征”。它要求学生能够创造数学符号表征非数学符号表征的情境。最后，“初步体会符号的使用是数学表达和数学思考的重要形式”④，这指向“符号操作”。它要求学生能够操作数学符号进行运算和推理，展开形式化的数学思考。

进一步分析可以发现，三个方面是紧密联系的。符号理解和符号表征是互逆的过程，一个是从符号到意义，另一个是从意义到符号。在没有符号之前，符号表征是符号理解的基础，即先根据意义创造符号表征，再由此理解符号的意义。而有了基本符号之后，符号理解则是符号表征的基础，即先理解基本符号的意义，再由此针对具体情境创造符号表征。在符号理解和符号表征的基础上，可以通过符号操作展开形式化的数学思考，从而获得数学结论，解决数学问题。此外需要指出的是，体会数学符号的特点特别重要，它有助于“感悟符号的数学功能”，形成符号表征和符号操作的意识。

实际上，布鲁纳的认知表征理论认为：智慧发展的一般进程是，从动作表征经图像表征而达到符号表征的世界。从这个角度看，在数学课程领域，符号意识其实就和核心素养的另一个主要表现——几何直观类似：几何直观是把图形视为重要的语言，读图，体会图形的特点（直观），并根据非图形表征的情境作图和用图，因而表现为图形理解、图形表征和图形操作三个方面（程茂山.也谈几何直观的培养［J］.教育研究与评论（小学教育教学），2022（9）：69。）；符号意识是把符号视为重要的语言，理解符号的意义，体会符号的特点，并根据非符号表征的情境创造符号和使用符号，因而表现为符号理解、符号表示、符号操作三个方面。

二、 符号意识的培养

根据上述符号意识三个方面表现的关系，在小学数学教学中，教师可以重点引导学生创造数学符号表示意义，操作数学符号发展意义，并在这一过程中充分理解数学符号的意义，体会（感悟）数学符号的特点（功能），从而培养学生的符号意识。

（一） 引导学生创造数学符号表示意义

数学源于对现实世界的抽象。数学研究对象和结论，或者说数学概念和命题，也就是数学意义，常常需要创造数学符号来表示（有时可以借助自然语言符号来表示）。教学中，教师要引导学生经历创造数学符号表示数学意义的过程，体会到数学符号表征既有“讲道理”的必然成分，也有“人为规定”的偶然成分，即“理性”的“创造”。这体现了弗赖登塔尔的“再创造”教育思想，能帮助学生充分理解数学符号的意义，体会数学符号的简约性、一般性特点，同时感受数学的文化本质。如果学生先入为主地记住了教材中采用的和要求掌握的现代通用的数学符号，教师要引导学生尝试创造不同的数学符号表示相同的数学意义，并适当展现数学史上人类创造过的不同的数学符号；同时，要引导学生比较不同的数学符号，体会它们的优劣。这正如波利亚所说的：“让你的学生提出问题，要不就像他们自己提问的那样由你去提出这些问题；让你的学生给出解答，要不就像他们自己给出的那样由你去给出解答。”（乔治·波利亚.数学的发现（第二卷）［M］.刘景麟，曹之江，邹清莲，译.呼和浩特：内蒙古人民出版社，1981：179。）例如，十进位值制记数法是算术发展史上的重大创造，而现代通用的阿拉伯数字是这一记数法的重要表现形式。在小学数学“数与运算”内容的教学中，教师要引导学生尝试创造数概念的符号表征（即记数法），通过手指记数、实物记数、结绳记数、刻痕记数、算筹记数、算盘记数、古罗马数字记数、汉字记数、阿拉伯数字记数等活动“再现”人类记数史（石志群.数学符号教学：基于原理，发挥价值［J］.教育研究与评论（中学教育教学），2022（3）：4546。），体会现代通用的阿拉伯数字所蕴含的简洁的“数码”思想（用不同的符号表示不同的数）、整体的“进制”思想（将多个小的计数单位组成一个大的计数单位）和直观的“位值”思想（用不同的位置表示不同的计数单位），认识其他记数法的不足（比如算筹记数、算盘记数、古罗马数字记数没有很好地体现“数码”思想，古罗马数字记数、汉字记数没有很好地体现“位值”思想）。同时说明：十进制记数法与非十进制（如二进制、八进制、十二进制、六十进制）记数法相比，并没有特别明显的优势，更多地是因为人类恰好有十个手指以及十这个数不大不小（表示常见的数时所用的数码和数位平衡得较好，都不多不少）而被广泛采用。

同样地，教学数的大小比较、四则运算以及分数概念、小数概念、负数概念乃至各种图形及其关系时，可以让学生尝试创造表示等于、不等于、大于、小于、加、减、乘、除、运算顺序、分数、小数、负数、点、线、角、三角形、四边形、圆、平行、垂直等含义的符号，并适当介绍有关符号的演变过程。（有关历史可参见：徐品芳，张红.数学符号史［M］.北京：科学出版社，2006；关于等号、不等号的教学案例可参见：刘劲苓，文静.数学文化素养话题之十一：等号和不等号［J］.教育视界，2022（29）。）

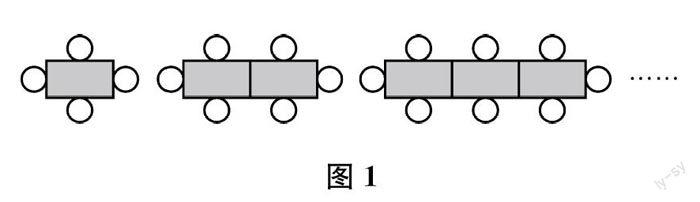
再如，字母表示数是代数发展史上的基础性创造。最初，字母表示的是确定的未知数（常量），由此发展出了方程方法；后来，字母可以表示不确定的任意数（变量），由此发展出了具有较强一般性的代数知识体系（包括函数内容）。在小学数学“数量关系”的教学中，教师要引导学生从具体的例子中寻找一般的数量关系，进而创造这些一般规律的符号表征，如用符号（字母式子）表示数位分解、因数分解以及和差关系、倍比关系、更复杂的组合关系，表示五种运算律以及一些有趣的运算规律，表示分數的基本性质、分数的四则运算法则，表示比例的基本性质、正比例关系、反比例关系，表示等式的基本性质，表示多边形的内角和公式、多种平面图形的面积公式、多种立体图形的体积公式，表示钉子板上的多边形的面积公式、图形缩放前后面积的变化规律、表面涂色的正方体的有关规律，表示诸如图1等所示的图形拼摆中的一般数量关系，表示现实中常见的诸如“路程=速度×时间”等的数量关系……体会其中“讲道理”的必然成分和“人为规定”的偶然成分。

这里值得一提的是，新课标在小学部分删去了方程的有关内容（移到了初中部分）。因此，在小学数学教学中，更多地要引导学生从不确定的任意数（变量）的角度看字母表示。比如，小明有x张漫画卡，小华比小明多5张漫画卡，那么小华有x+5张漫画卡。这一信息放在可用方程求解的具体问题中时，x可以是确定的未知数（常量），但教师更多地要引导学生体会“x+5表示比x多5的数量”的一般性。

（二） 引导学生操作数学符号发展意义

数学在抽象的基础上，通过对研究对象和结论的形式化运算和推理获得进一步发展，形成更多的结论和方法，即抽象结构。这里的形式化运算和推理主要表现为符号操作。教学中，有了数学符号表征之后，教师要引导学生根据形式化规则操作数学符号，获得新的数学符号表征，从而发展新的意义。在这一过程中，学生能更充分地体会到数学符号的简约性、一般性特点，形成良好的符号意识。

例如，在小学数学“数与运算”内容的教学中，在学生理解了“相同计数单位的个数相加减”以及“个数和个数相乘除得到结果的个数，计数单位和计数单位相乘除得到结果的计数单位”的算理之后（一开始不是很理解的话，也可以在具体计算中慢慢理解），教师可以引导学生探索基于现代通用的阿拉伯数字（记数符号）的计算形式（规则），从而实现以20以内的不进位、进位加法和不退位、退位减法以及表内乘法和除法计算为基础，通过符号操作完成多位数乃至小数的四则运算（主要指向现代常用的竖式，也可以是其他形式，如乘法的“铺地锦”）。有了合适的计算形式（规则），学生不需要具体地考虑（就像计算20以内的不进位、进位加法和不退位、退位减法以及表内乘法和除法那样）两个数的运算结果是多少，而只需要对数字（记数符号）进行相应的符号操作，得到最终的符号表征，从而体会到形式化的符号操作因为不考虑情境背景和具体意义而简化了思维，具有简约性。与此同时，教师还可以引导学生探索、比较基于其他记数法的四则运算形式（规则），从中深入体会阿拉伯数字的优越性。

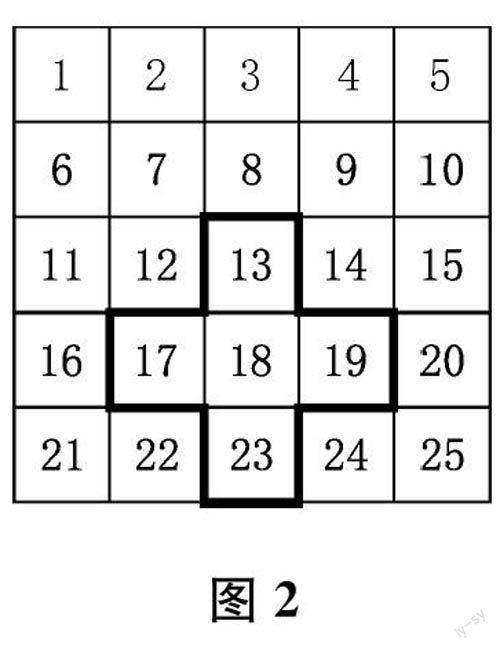
再如，在小学数学“数量关系”内容的教学中，教师可以引导学生基于数位分解、因数分解、和差关系、倍比关系等的符号表征（字母式子），通过利用运算律进行式子变形（符号操作），得到（或说明）一些有趣的运算规律。以苏教版小学数学三年级下册“有趣的乘法计算”的教学为例，可以通过（10a+b）×11=110a+11b=100a+10（a+b）+b的符号操作说明两位数乘11的计算规律，也可以通过（10a+b）（10a+10-b）=100a（a+1）-10ab+10ab+b（10-b）=100a（a+1）+b（10-b）的符号操作说明“头同尾合十”的两位数乘法计算规律。同样地，“和与积的奇偶性”“3的倍数的特征”乃至在图2中用“十字形”任意框出的五个数之和与中间数的关系等一般的数量关系（规律），都可以基于一般化的符号表征（字母式子），通过符号操作（利用运算律进行式子变形）得到（或说明）。

此外，列方程解决实际问题是最典型的先创造数学符号（列方程）表示意义，再操作数学符号（利用性质解方程，不考虑实际意义）发展意义（得结果，还具有实际意义）的过程，可以充分展现数学符号的简约性、一般性。虽然方程的有关内容移到了初中，但是在小学数学教学中，教师还可以适当渗透方程思想，以体现符号表征与操作在解决问题时的优势。例如，实际问题“甲库搬出240袋水泥到乙库后，甲库还比乙库多130袋，则原来乙库比甲库少多少袋”，因为比常见的“谁给谁后就同样多”的问题更复杂，学生解决时常常理不清数量关系。如果借助符号表征和操作来解决，则很简单：由（甲-240）-（乙+240）=130，得（甲-乙）=610。

最后需要指出的是，虽然在创造数学符号表示意义以及操作数学符号发展意义的过程中，学生可以较好地理解符号的意义，但是，因为符号具有不同程度的抽象性，其意义也常常可以变化。因此，教师还需要注意反过来，引导学生阅读所给符号，适当发散思维，解释各种可能的意义。比如，将“0”理解为“没有”或“一种临界状态”。再如，将“=”理解为“计算结果”或“等量关系”。又如，将“2a+2b”理解为长方形周长的一般形式。

（高慧，南京师范大学附属中学新城小学北校区。）