在椭圆横截面弹体正侵彻下有限厚铝靶的破坏模式及响应特性*

刘均伟，张先锋，赵瑶瑶，魏海洋,3，刘 闯，李鹏程

（1. 南京理工大学机械工程学院，江苏 南京 210094；2. 江苏永丰机械有限责任公司，江苏 淮安 211722；3. 北京航天长征飞行器研究所，北京 100074）

目前，相较于圆形横截面弹体，各种非圆横截面弹体由于具有在高超声速武器平台上适应性好、装填比大、抗弯强度高及平台内部有效载荷空间利用率高等优点已成为研究热点[1-3]。诸多学者在异形弹体对目标的侵彻与贯穿作用机理方面已开展了大量研究工作。Ben-Dor 等[4-5]、Yakunina[6-7]通过研究发现，对于弹体在稠密介质中的侵彻问题，非圆横截面弹体（多圆锥体切面）为最优的弹体结构形状，能够有效降低靶体侵彻阻力。Woo[8]基于傅里叶级数展开和最小二乘法，研究了以压力/速度边界条件控制的任意截面形状的空腔膨胀时空腔边界的应力分布特性，通过比较发现非圆横截面弹体具有更优异的侵彻性能。Bless[9]针对矩形横截面弹体和圆形横截面弹体进行了高速侵彻实验，分析了这2 种弹体的侵彻效率，发现非对称横截面弹体在临界速度以下的侵彻性能更优异。杜忠华等[10-11]开展了圆形、矩形和三角形3 类横截面弹体侵彻半无限金属板的实验和理论研究，发现在弹体最大横截面面积和初始速度相同的情况下，三角形横截面弹体的侵彻效率最高，矩形横截面弹体的侵彻效率次之，而圆形横截面弹体的侵彻效率最低。高光发等[12]基于杜忠华等[10-11]的实验结果，开展了相应的数值模拟，进一步验证了杜忠华等[10-11]的发现。Dong 等[13-14]、Gao 等[15]、高旭东等[16]开展了一系列椭圆横截面弹体侵彻半无限厚混凝土靶的实验，弹体横截面长短轴长度比分别为1.5 和2.0，实验数据表明，椭圆横截面弹体在700～1 000 m/s 的撞击速度范围内具有良好的侵彻性能和弹道稳定性；同时，通过数值模拟研究了椭圆横截面弹体侵彻混凝土靶的受力特性，结果表明，在相同侵彻速度下，弹体头部的法向应力从弹体横截面长轴方向向短轴方向逐渐升高。在有限厚靶板方面，王浩等[17-18]开展了椭圆横截面弹体正贯穿加筋板的研究，获得了椭圆横截面弹体剩余速度和靶板弹道极限速度的预测公式，发现随着椭圆弹体横截面长短轴长度比的增大，靶板的弹道极限速度近似线性升高。Landkof 等[19]基于刚塑性模型假设和能量守恒原理，考虑了裂纹传播、花瓣弯曲和靶板整体凹陷变形能，建立了锥形弹体正侵彻薄铝板弹道极限速度计算模型。张中国等[20]和Chen 等[21]开展了加筋板贯穿实验研究，讨论了加强筋对靶板破坏模式和弹道参数的影响，分析了靶板吸收能量的情况，根据实验数据修正了De Marre 贯穿经验公式。Song 等[22]和徐双喜等[23]同样基于刚塑性模型假设和能量守恒原理，分别对截卵形弹体和截锥形弹体贯穿加筋钢板进行了理论分析。

弹靶作用过程是一个复杂的动力学问题，在异形横截面弹体对目标的侵彻作用过程研究中，对弹体阻力以及侵彻剩余速度和侵彻深度的研究较广泛，而关于弹体侵彻作用下靶体响应特性的研究工作报道较少。研究异形横截面弹体侵彻作用下靶体破坏模式及响应特性对理解靶体非对称破坏、变形和耗能特性以及建立靶体阻力函数等具有重要意义。因此，本文中设计并开展3 种不同横截面弹体正侵彻2A12 铝板的实验研究，获得椭圆横截面弹体对2A12 铝板的破坏特性及弹体剩余速度；在此基础上，建立椭圆横截面弹体正侵彻2A12 铝板的数值模拟模型，结合实验结果验证模型的有效性，并从工程应用的角度，研究不同横截面弹体正侵彻铝板的剩余速度；另外，系统分析弹体横截面长短轴长度比对靶体破坏情况及响应特性的影响，包括靶体两侧花瓣的大小、形状和分布规律，靶体塑性应变区域的范围以及在弹体头部贯入阶段靶体沿周向各点的径向位移、径向应力和切向应力的变化规律等。

1 实 验

1.1 弹体和靶体

为了研究不同横截面形状弹体正侵彻铝板的破坏特性，开展了椭圆横截面弹体正侵彻铝板的实验。弹体材料为30CrMnSiNi2A 高强度钢，经淬火处理后洛氏硬度HRC 为55 ，屈服强度约为1 600 MPa。实验弹体如图1 所示，包括3 种弹型：C1 型弹、T1 型弹和T2 型弹。弹体主要参数见表1，a和b分别为弹体横截面长、短半轴长，β 为弹体横截面的长短轴长度比，L为弹体头部的长度，ψ 为弹体头部曲径比，m为弹体的质量。椭圆横截面弹体的头部曲径比不是一个常数，它与方位角密切相关，即沿圆周方向由长轴向短轴逐渐增大[2]，本文中所用曲径比均为短轴方向的曲径比。

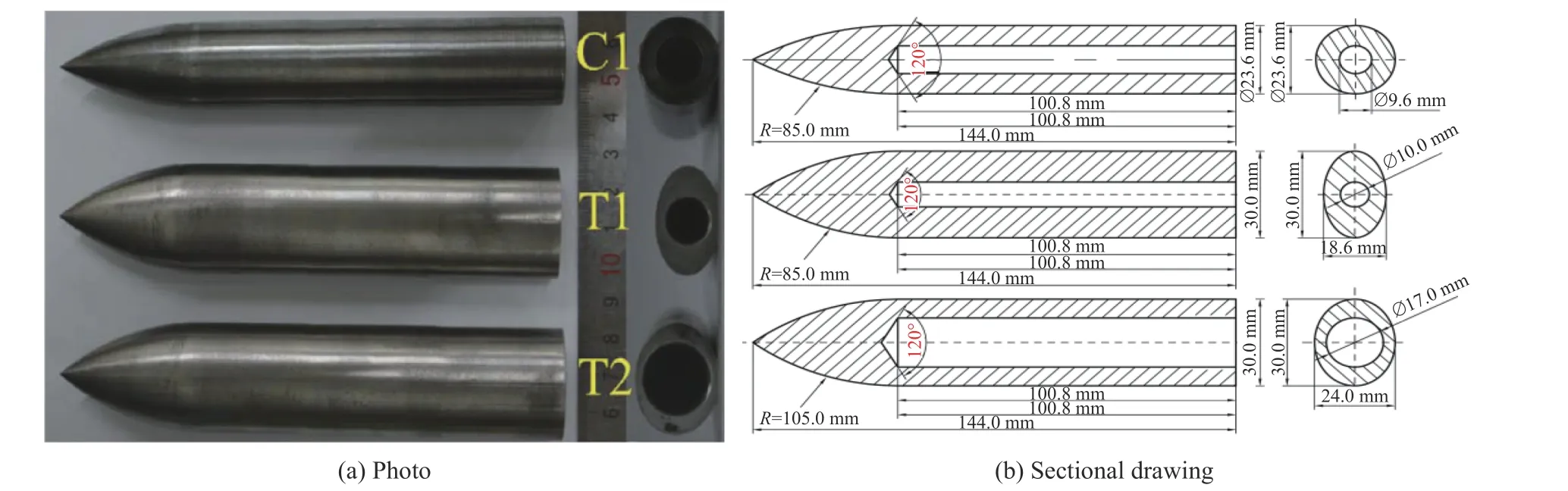
图1 实验弹体Fig. 1 Projectiles used in the experiments

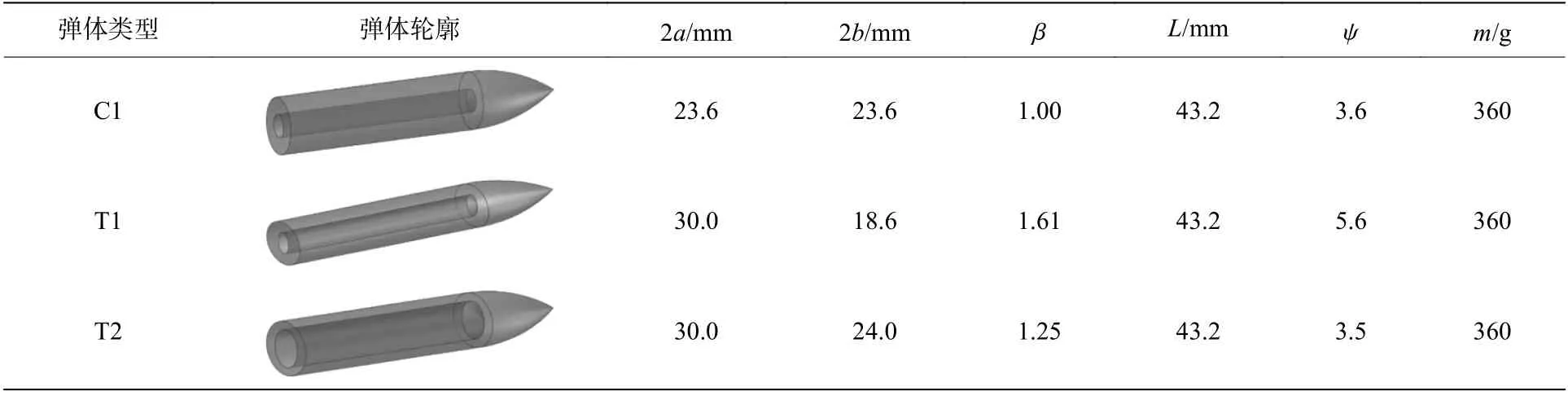
表1 三种弹体主要参数Table 1 Main parameters of three projectiles

为保证侵彻弹体的完整性以研究弹体横截面形状对靶体破坏效应的影响，选用强度较低（屈服强度约为200 MPa）的2A12 铝合金作为靶体材料。靶体尺寸设为400 mm×400 mm×30 mm 以忽略靶体两侧自由面对靶体响应的影响，如图2 所示。实验现场布置如图3 所示，采用高速摄像机观察弹体飞行姿态，同时将2 个平面镜分别放置于靶前和靶后弹体运动轨迹的正下方，与水平面呈45°夹角，通过测量和分析弹体与平面镜中弹体的位置变化，得到弹体的速度、运动轨迹和姿态。

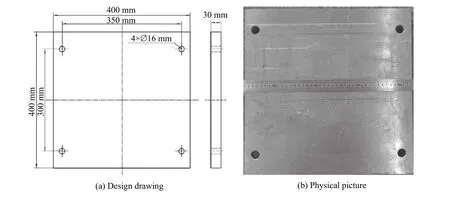
图2 实验靶体Fig. 2 Targets used in the experiments

图3 实验布局Fig. 3 Experimental layout

1.2 实验结果

共开展了10 发实验，其中C1 型弹体4 发，T1 和T2 型弹体各3 发，通过调整发射药量控制弹体速度在200～600 m/s。C1-4 弹体飞行姿态如图4 所示，根据高速摄影以及平面镜成像可以核定弹体的着靶姿态、初始撞击速度和剩余速度，实验结果见表2，v0为弹体初始撞击速度，vr为弹体剩余速度， α 为弹体的着靶角， γ 为弹体的偏航角。从表2 中可以看出：3 种弹体的初始撞击速度基本相同，具有一定的可比性；弹体最大着靶角 α 为2.69°，最大偏航角 γ 为-2.39°，基本满足正侵彻条件。

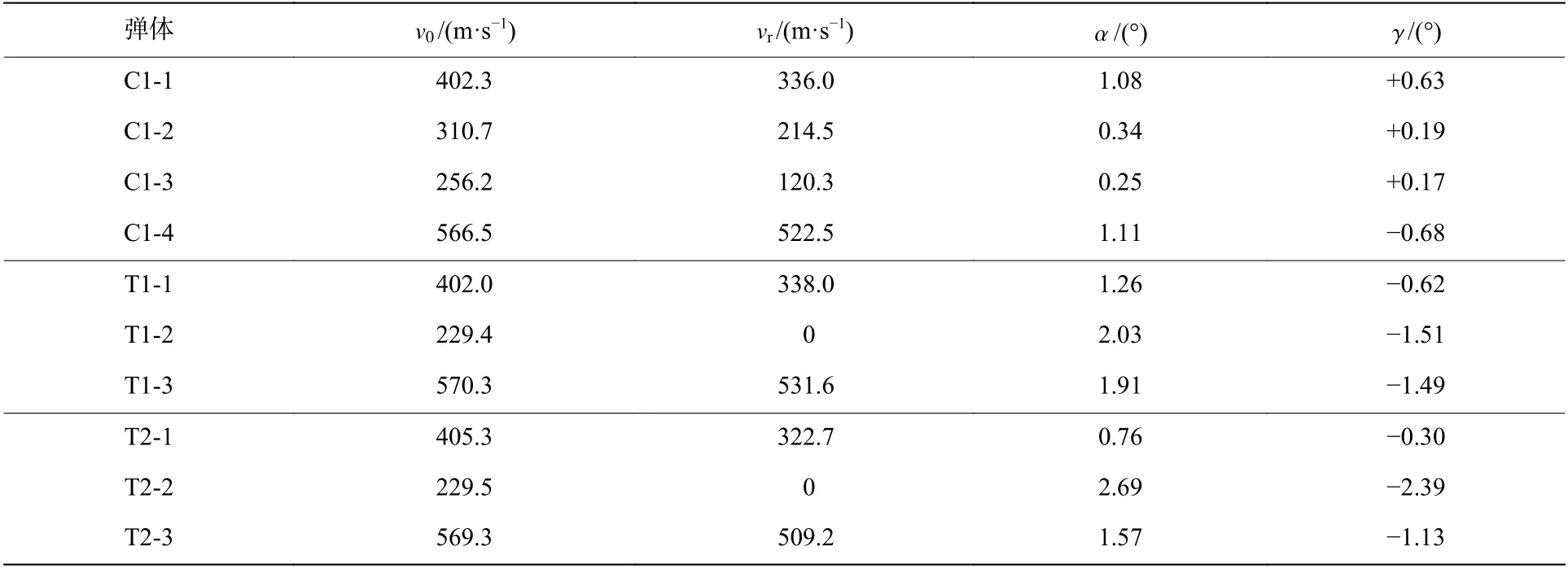
表2 弹体正侵彻铝靶的实验结果Table 2 Experimental results for normal penetration of projectiles into aluminum targets

图4 C1-4 弹体飞行姿态分析Fig. 4 Analysis of the flight attitude of the C1-4 projectile

C1-4 弹体侵彻铝靶前后的对比如图5 所示，弹体长度和形状无明显变化，仅表面有一定的摩擦痕迹，因此，弹体正侵彻铝靶的过程可视为刚体侵彻过程。

图5 实验前后C1-4 弹体对比Fig. 5 Comparison of the C1-4 projectile before and after the experiment

图6 为在3 种不同横截面形状弹体侵彻下铝靶的破坏形貌。可知，C1 型弹体贯穿铝靶后，在铝靶正面形成近似圆形的弹孔，孔径略大于弹体的直径，铝靶背面形成多个花瓣，且花瓣大小、分布较均匀；T1 和T2 型弹体与C1 型弹体类似，在铝靶正面形成近似弹体最大横截面形状和尺寸的孔洞，而铝靶背面的花瓣大小和分布与C1 型弹体侵彻下的有较大区别，靶体破坏情况呈现不对称性，表现为靶体孔洞横截面短轴方向的花瓣大于长轴方向的，部分靶体孔洞横截面长轴方向的花瓣甚至发生了崩落。这与文献[24]的结论一致，由于椭圆横截面空腔边界位移的不均匀性，空腔边界应力分布呈现从长轴至短轴逐渐降低的趋势，因此长轴方向受力更高。

图6 不同横截面形状弹体侵彻下铝靶的破坏形貌Fig. 6 Damage of aluminum targets under normal penetration of the projectiles with different cross-section shapes

2 数值模拟

2.1 有限元模型及材料参数

采用LS-DYNA 软件对铝靶在不同横截面形状的弹体正侵彻下的破坏特性进行数值模拟分析。铝板和弹体均采用八节点六面体单元，单元算法为拉格朗日算法。为了节约CPU 资源、提高数值模拟计算效率，整个模型采用1/4 建模，铝靶迎弹面的中心区域网格划分密集，网格大小为0.25 mm×0.25 mm×0.3 mm，网格从中心沿四周采用3 次蝴蝶网格过渡，中心区网格密集区域为10 倍弹径，弹靶有限元模型如图7 所示。通过关键字BOUNDARY_SPC_SET 设置对称面约束，弹体和靶体之间通过关键字CONTACT_ERODING_NODES_TO_SURFACE 设置侵蚀接触，在靶板两侧边缘面设置无反射边界条件，并施加固定约束，保证数值模拟的初始条件与实验中初始条件一致。

图7 有限元模型Fig. 7 Finite element models

从实验回收弹体可以看出弹体正侵彻薄铝靶的过程可视为刚体侵彻，因此对弹体采用MAT_RIGID刚体模型，而对铝靶则采用高应变率下适用的JOHNSON_COOK (JC)材料模型和GRÜNEISEN 状态方程共同表征，具体材料参数如表3 所示。表3 中A、B、C、m和n分别为静态屈服强度、硬化系数、硬化指数、温度软化指数和应变率系数， ρ 、G和µ分别为材料的密度、剪切强度和泊松比。

表3 材料参数Table 3 Material parameters

2.2 数值模型准确性验证

根据实验初始条件，对不同横截面弹体正侵彻铝靶过程进行了模拟。从表4 可以看到，数值模拟的弹体剩余速度与实验结果吻合较好，相对误差ɛr最大为9.2%。从图8 可以发现，数值模拟得到的3 种横截面弹体正侵彻铝靶的破坏形貌与实验结果吻合良好，仅部分铝靶孔洞边缘处一些尺寸较小的花瓣与实验结果有一定差距，这可能是由于单元侵蚀算法将部分畸变严重网格删除所致。数值模拟结果中靶板破坏情况与实验结果基本吻合，表明本文中使用的网格尺寸、材料模型及参数等是合理的，能较好地模拟不同横截面弹体正侵彻下铝靶的结构响应和破坏模式，后续可依据此模型对不同横截面弹体正侵彻下铝靶的力学行为进行分析和预测。

图8 实验靶板破坏形态与数值模拟结果对比Fig. 8 Comparison of failure morphologies of targets between simulation and experiment

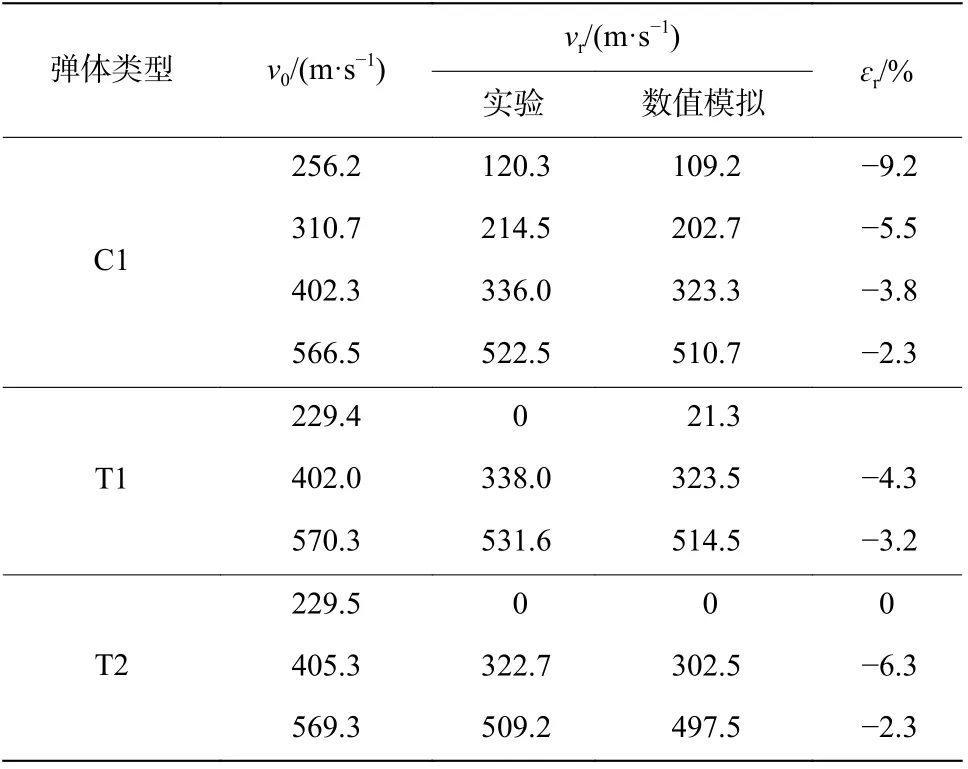
表4 弹体剩余速度模拟结果与实验结果的对比Table 4 Comparison of residual velocities of projectiles between simulation and experiment

3 椭圆横截面弹体正侵彻有限厚铝靶作用特性数值模拟分析

基于已验证的数值模型，系统研究了弹体椭圆横截面长短轴长度比对靶体破坏情况以及响应特性的影响，包括靶体两侧的花瓣大小、形状和分布规律，以及靶体塑性应变区域的范围等，并从工程应用的角度，计算了不同横截面形状弹体正侵彻铝靶后的剩余速度；同时在极坐标系中研究了在弹体头部贯入阶段靶体沿周向各点的径向位移、径向应力和切向应力的变化规律。

3.1 不同横截面形状弹体正侵彻铝靶后的剩余速度

为研究弹体椭圆横截面长短轴长度比对弹体剩余速度的影响，根据C1 和T1 弹体，在保证弹体横截面面积相同的情况下设计了2 种椭圆横截面弹体（T3 和T4 弹体），这4 种弹体横截面长短轴长度比β 分别为1.00、1.61、1.25 和2.00，弹体的初始速度v0为200～600 m/s，计算相应的剩余速度vr，如图9 所示，S为该弹体的最大横截面面积。通过调整弹身部分的开孔尺寸，保证各弹体的质量和头部长度一致。

从图9 可以看出，C1、T1、T3 和T4 型弹体的剩余速度差异较小，这表明椭圆弹体横截面长短轴长度比对其剩余速度的影响较弱。因此，在工程应用中，可直接使用圆形横截面弹体正贯穿靶板的工程模型来计算具有相同最大横截面面积的椭圆横截面弹体的剩余速度。T2 和T3 型弹体虽然具有相同的横截面长短轴长度比，但T2 型弹体的最大横截面面积大于T3 型弹体的，从两者的剩余速度曲线可以看出，T2 型弹体的剩余速度低于T3 型弹体的，这意味着弹体最大横截面面积对其正侵彻靶板后的剩余速度影响较显著。在设计弹体结构时，在保证弹体强度和刚度的情况下，尽量减小弹体的最大横截面面积以提高弹体穿靶后的剩余速度。

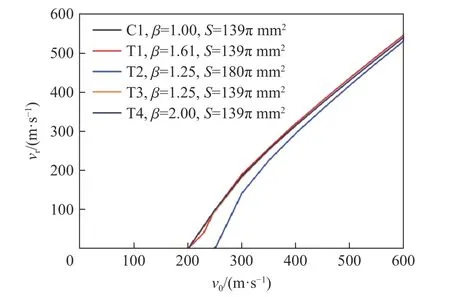
图9 不同横截面形状弹体剩余速度对比Fig. 9 Comparison of residual velocities of projectiles with different cross-section shapes

3.2 弹体横截面长短轴长度比对靶体破坏情况及响应特性的影响

为分析椭圆横截面弹体长短轴长度比对靶体破坏情况的影响，以长短轴长度比β 分别为1.00、1.25、1.61 和2.00 的4 种弹体（质量、长度、最大横截面面积等均一致）为计算模型，分析在400 m/s 弹体撞击速度下靶体破坏情况及响应特性的差异，如图10～11 所示。

从图10 可以看出，圆形与椭圆横截面弹体侵彻作用下靶体的破坏程度有一定差异（图中长轴方向为长轴平视图，即弹道边缘对应弹体长轴）。从靶体背部的花瓣数量来看，β=1.00 的C1 型弹体侵彻造成的花瓣数量最少（6 个），而β=2.00 的T4 型弹体侵彻造成的花瓣数量最多（多于20 个）。从花瓣的形态分析，前者靶体背部的花瓣大小一致、形状规则，且分布均匀，而后者靶体背部的花瓣则大小不一、形状不规则，且分布角度差距较大。总的来说，弹体横截面长短轴长度比越大，侵彻后靶体背部的花瓣数量越多，尺寸越小，且短轴方向的花瓣数量和靶体表面隆起高度大于长轴方向的。此外，从塑性应变分布可以看出，在花瓣处的应变值明显高于其余位置的，且长轴方向的高塑性应变区域更集中，意味着靶体在长轴方向受力更高，容易产生破坏，这也解释了实验中所观察到长轴方向花瓣发生的崩落现象。

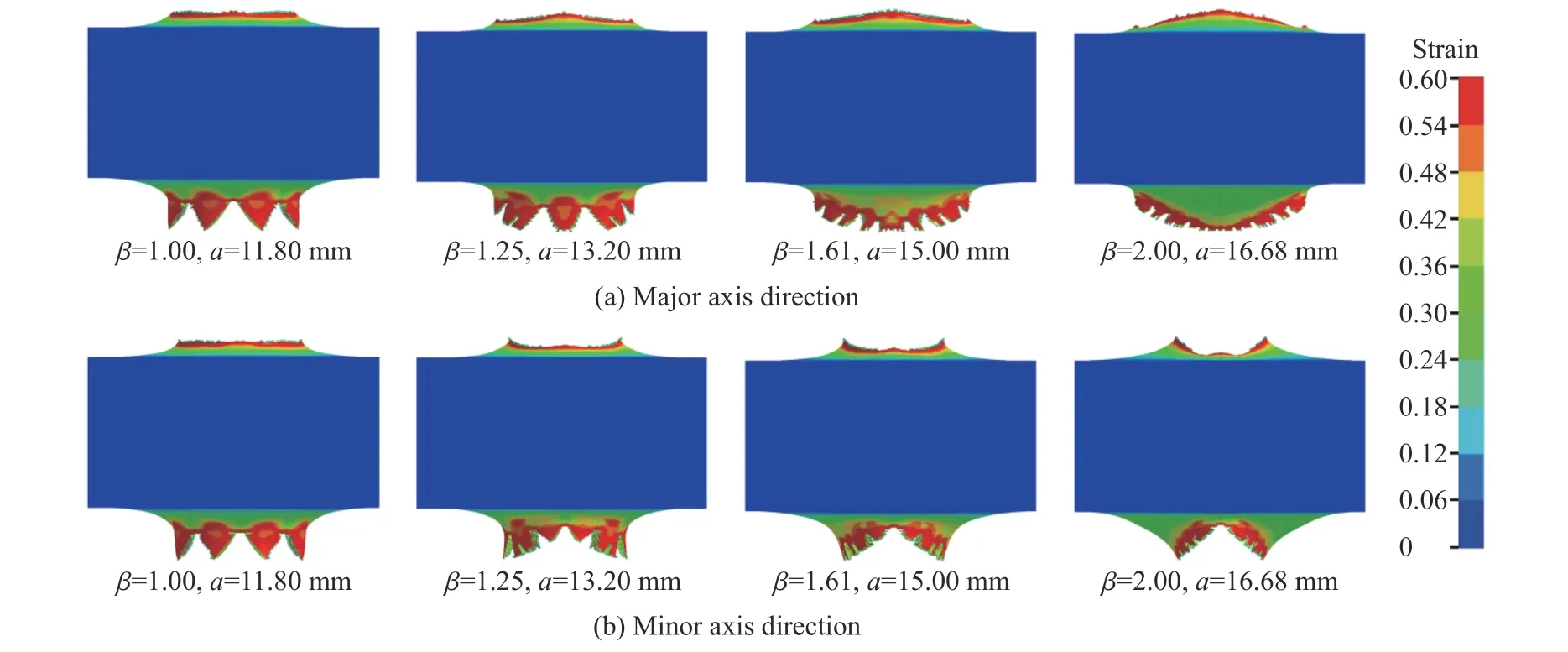
图10 弹体横截面长短轴长度比对靶体破坏形貌的影响Fig. 10 Influence of major-to-minor axis length ratios of the projectile cross-sections on damage morphologies of the targets

从图11 可以看出：圆形横截面弹体侵彻作用下靶体表面、背部塑性应变区域为圆形；其余3 种椭圆横截面弹体侵彻作用下靶体表面、背部塑性应变区域呈现类椭圆形，同时长轴方向的塑性应变影响范围明显小于短轴方向的。

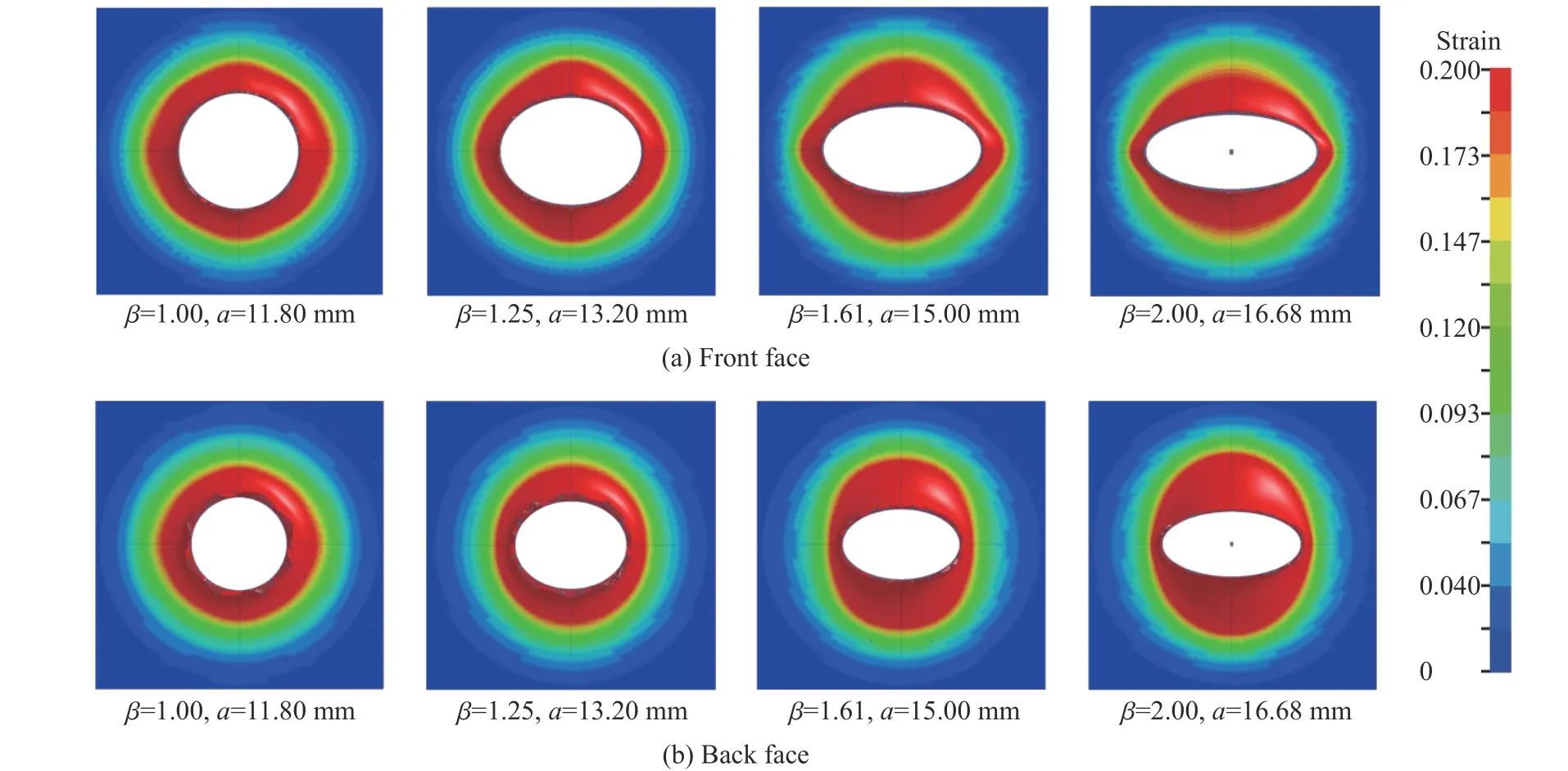
图11 靶体应变分布Fig. 11 Strain distribution of the targets

表5 中统计了在靶体背部长/短轴方向上塑性应变不超过0.2 的区域的最大坐标值，定义长/短轴相对增量=（长/短轴最大坐标值-长/短轴半轴长）÷（长/短轴半轴长），表征靶体在长/短轴方向塑性应变区域的增大比例。表5 中数据表明，随着长短轴长度比的增大，长轴相对增量逐渐减小，短轴相对增量逐渐增大，塑性应变区域的不对称性逐渐加剧。

表5 靶体背部塑性应变区域范围对比Table 5 Comparison of plastic strain ranges on the back of targets

3.3 极坐标系下弹体横截面长短轴长度比对靶体响应特性的影响

在弹体的侵彻理论模型中，靶体的径向/法向应力是学者们更关注的问题，其与靶体阻力函数密切相关，直接影响理论模型的准确性。因此，通过在数值模拟后处理软件中建立极坐标系的方法，分析不同椭圆横截面长短轴长度比的弹体侵彻作用下靶体的响应特性。忽略靶体自由面效应及边界效应对计算结果的影响，仅提取弹体头部贯入阶段靶体沿周向各点的各项参数，靶体测量点位置如图12 所示，在400 m/s 的初始撞击速度下，弹体头部贯入阶段持续约80 µs。

图12 数值模拟中靶体测点分布Fig. 12 Layout of measured points of targets in numerical simulation

图13～15 给出了不同长短轴长度比的椭圆横截面弹体侵彻作用下，各测量点的径向位移、径向应力及切向应力的变化情况。从图13～14 可以看出，圆形与椭圆横截面弹体侵彻作用下靶体的响应特性有显著区别。从靶体的径向位移和径向应力来看，前者在周向方向的变化趋势基本一致，各测量点提取的数据曲线重合，表明靶体的响应沿周向是均匀的；而后者在周向的各点表现出较大的差异，主要如下：(1)各测量点的径向位移和径向应力峰值不同，峰值呈现出从短轴至长轴逐渐降低的趋势；(2)各测量点的径向位移和径向应力达到峰值的时间不同，长轴方向最先达到峰值，而在短轴方向最晚；(3)径向位移和径向应力峰值大小和比值与弹体横截面长短轴长度比有关。

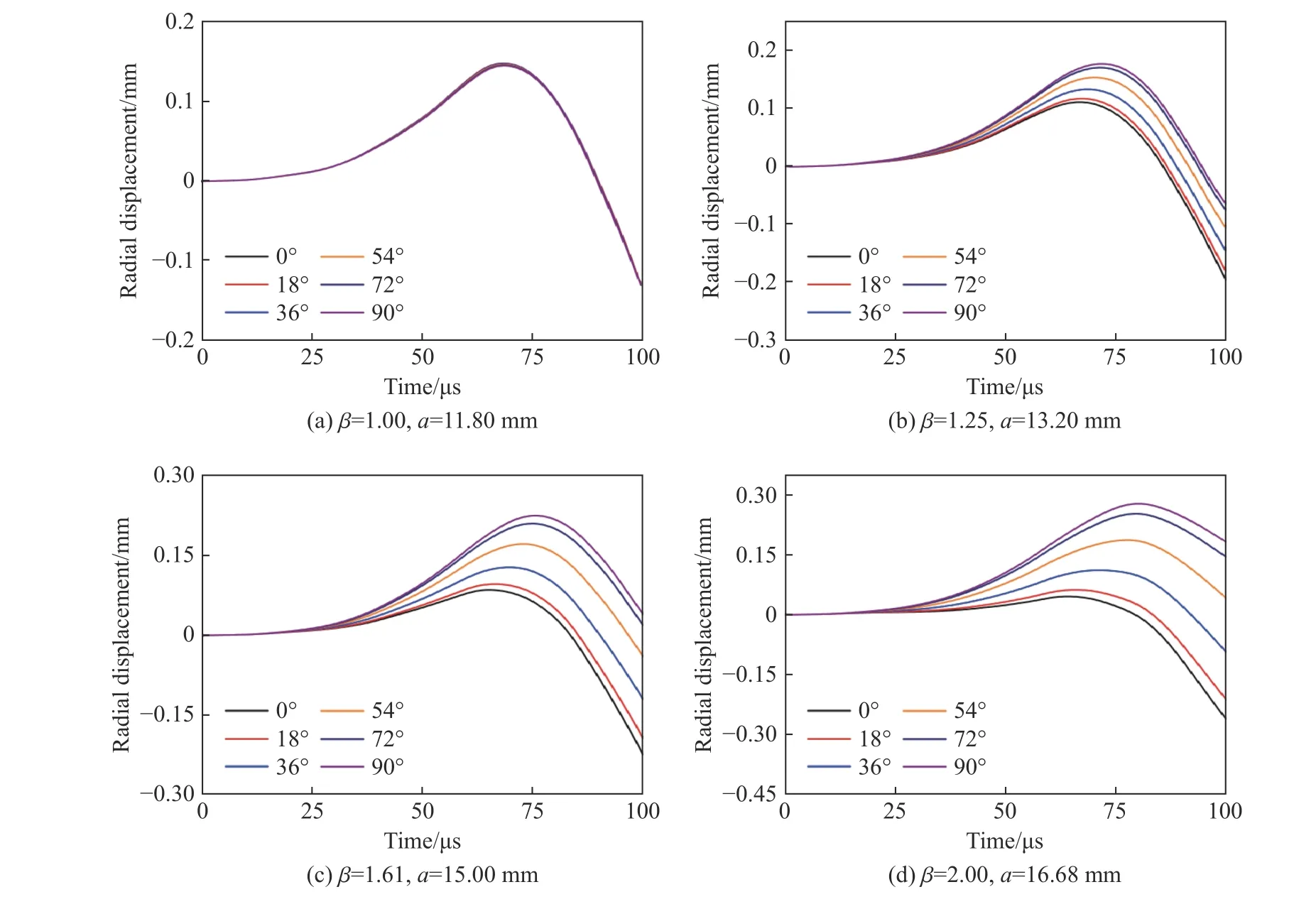
图13 靶体沿周向方向的径向位移Fig. 13 Radial displacement of targets along circumferential direction

从图15(a)可以发现，靶体在各点的切向应力基本为零，这是由于圆形横截面弹体为旋转对称结构，在理想侵彻条件（弹体刚性、无倾角/攻角/偏航角）下，靶体在各方向的变形一致且仅沿着径向方向，因此切向方向无变形，切向应力为零；而椭圆横截面弹体则是面对称结构，导致靶体除了在弹体对称面（长/短轴平面）上仅沿径向变形，而在其余方向同时具有径向变形和切向变形；因此切向应力在0°和90°方向为零，在0°与90°之间呈现先升高后降低的趋势，如图15(b)～(d)所示。

图14 靶体沿周向方向的径向应力Fig. 14 Radial stress of targets along circumferential direction

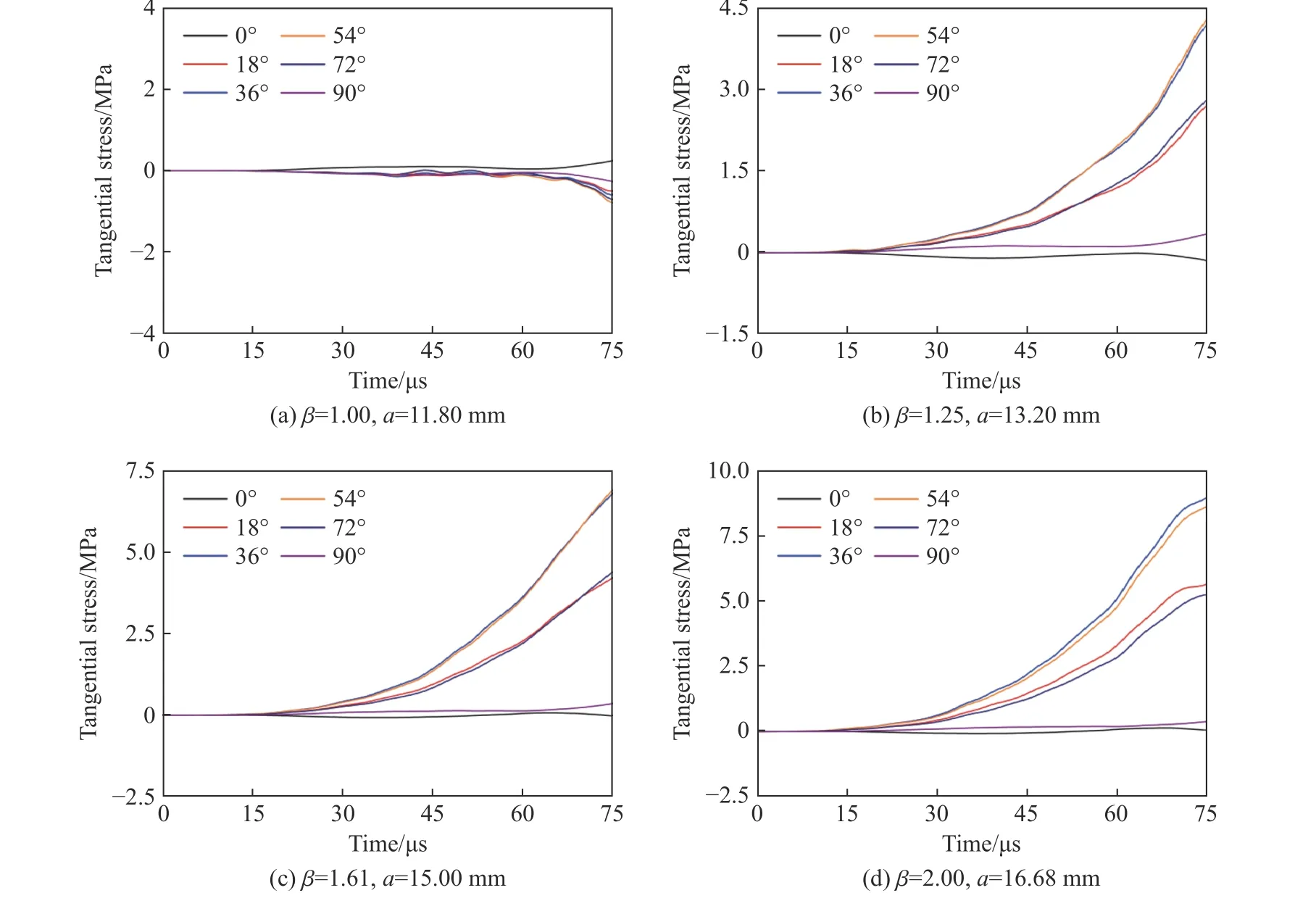
图15 靶体沿周向方向的切向应力Fig. 15 Tangential stress of targets along circumferential direction

为了直观分析弹体横截面长短轴长度比对靶体响应特性的影响规律，将径向位移和径向应力的峰值做无量纲化处理，同时提取切向应力的峰值进行研究，如图16～18 所示。从图中可以看到弹体横截面长短轴长度比对靶体的径向位移/应力和切向应力的影响显著，长短轴长度比越大，径向位移/应力和切向应力的不对称性越明显；径向位移/应力从长轴至短轴逐渐增加，同时变化梯度呈现先增加后减小的趋势，类似于三角函数。而靶体的切向应力（除圆形横截面弹体外）则表现先增加后减小的变化规律，切向应力关于45°方向基本呈现对称分布；此外，随着长短轴长度比的增大，切向应力的峰值提升显著。

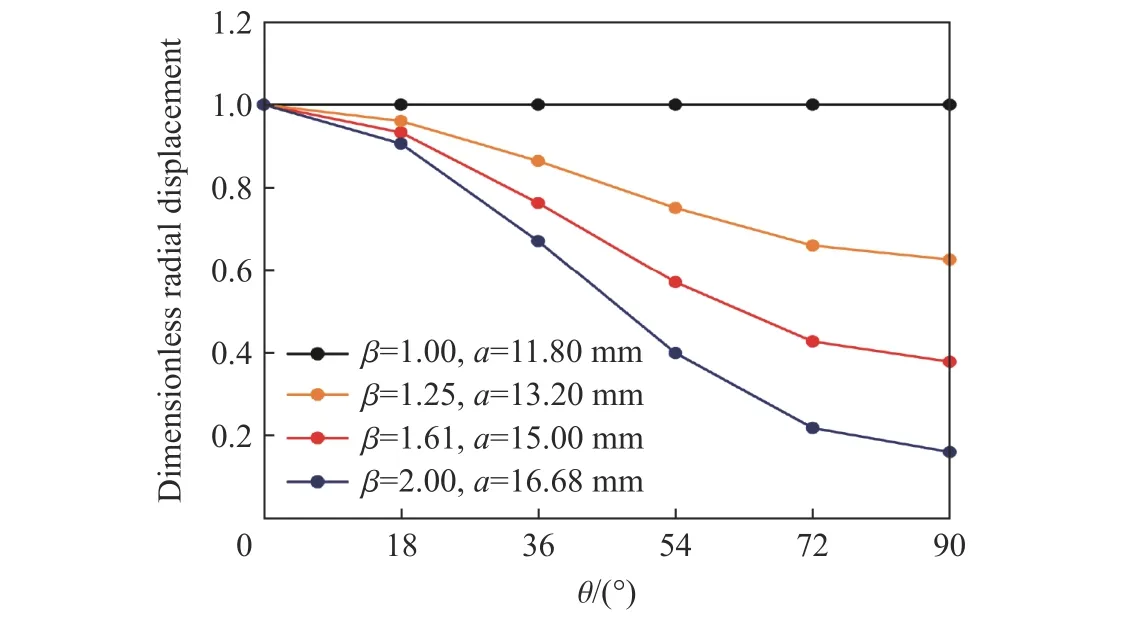
图16 沿周向方向的无量纲径向位移Fig. 16 Dimensionless radial displacement of targets along circumferential direction

图13～18 的数值模拟结果表明，在圆形横截面弹体侵彻作用下，靶体沿周向方向各测量点的响应曲线基本一致，靶体各点仅受径向应力作用而切向应力为零，因此绝大部分圆形横截面弹体的侵彻理论模型将弹靶作用过程简化为一维是合理的；在椭圆横截面弹体侵彻作用下，靶体沿周向方向各测量点的响应曲线则存在明显的非对称特性，靶体各点径向位移和径向应力峰值、峰值到达时间、峰值比值等与周向角密切相关。不考虑靶体反射形成的拉伸波的情况下，靶体也不再是处于简单的压缩状态，而是处于压缩/剪切的复杂应力状态，因此针对椭圆横截面弹体的侵彻理论模型应着重考虑靶体复杂应力状态对靶体阻力函数的影响。

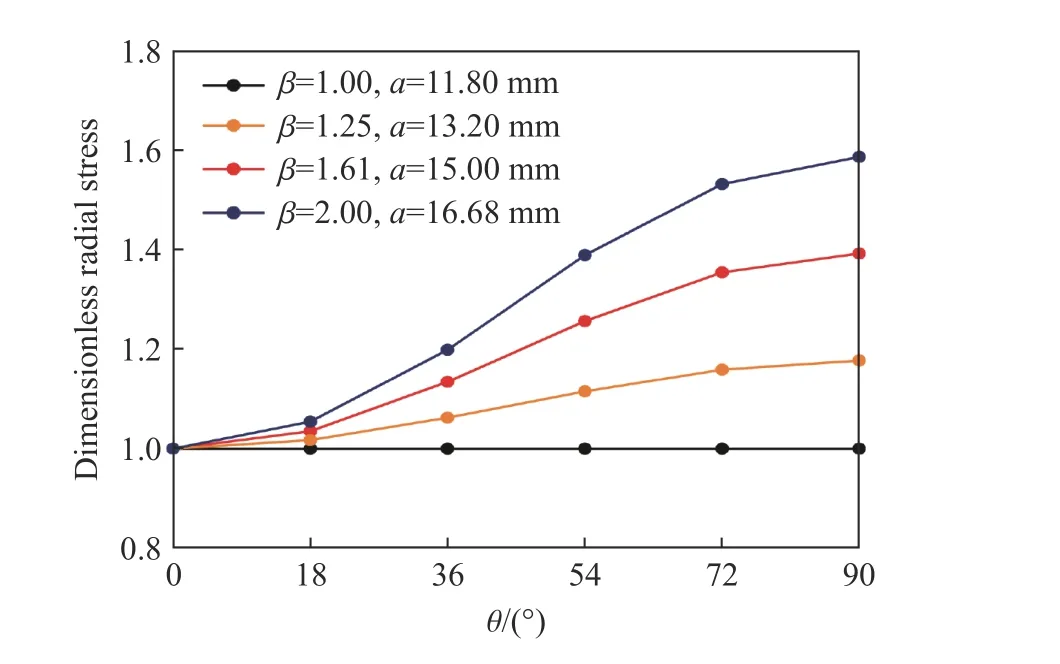
图17 沿周向方向的无量纲径向应力Fig. 17 Dimensionless radial stress of targets along circumferential direction

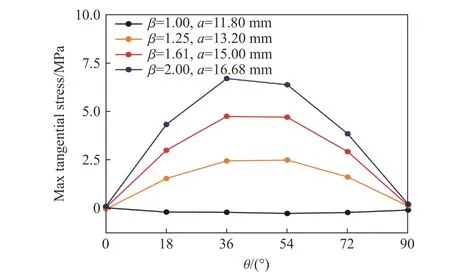
图18 沿周向方向的最大切向应力Fig. 18 The maximum tangential stress of targets along circumferential direction

4 结 论

开展了3 种不同椭圆横截面弹体（弹体横截面长短轴长度比β=1.00, 1.25, 1.61）在200～600 m/s 撞击速度范围内正侵彻2A12 铝板的实验，获得了2A12 铝板的破坏特征及弹体的剩余速度。在此基础上，建立了相应的数值模拟模型，结合实验结果验证了模型的有效性，并系统分析了弹体横截面长短轴长度比对靶体破坏情况及响应特性的影响，主要结论如下。

(1)弹体最大横截面面积是影响弹体剩余速度的主要因素，弹体横截面长短轴长度比对其剩余速度的影响较小。在工程应用中，可直接使用圆形横截面弹体正贯穿靶板的工程模型来计算具有相同最大横截面面积的椭圆横截面弹体的剩余速度。

(2)弹体横截面长短轴长度比对靶体的破坏程度有较大影响。当β=1.00 时，靶体背部形成的花瓣大小和形状一致、空间分布均匀，而随着长短轴长度比的增大，花瓣数量增加，尺寸变小，且短轴方向的花瓣数量、靶体表面隆起高度大于长轴方向的。

(3)弹体横截面长短轴长度比对靶体响应特性有显著影响。在圆形横截面弹体侵彻作用下，靶体背部的塑性应变区域为圆形；而在椭圆横截面弹体侵彻作用下，靶体背部的塑性应变区域则近似于椭圆形，且沿短轴方向的塑性应变区域明显大于沿长轴方向的塑性应变区域。

(4)在圆形横截面弹体侵彻作用下，靶体的径向位移、径向应力和切向应力与在椭圆横截面弹体侵彻作用下靶体的径向位移、径向应力和切向应力显著不同：前者靶体沿周向方向各点的应力状态变化规律基本一致，靶体处于简单的压缩状态，切向应力为零；后者靶体各点的应力状态与弹体横截面长短轴长度比和周向角密切相关，靶体各点同时受到压缩和剪切应力的耦合作用。