基于EMD-LSTM的血小板需求预测研究

蒲 松

(成都工业学院 经济与管理学院，成都 611730)

血液的短缺会严重影响患者的治疗，导致死亡率的增加[1-2]。学者研究了血液中心医院的库存管理策略，通过有效的库存管理策略较好地解决血液需求的不确定性，减少血液的浪费[3]。但是，血液的易腐性给库存管理带来了极大的挑战。特别是血小板，因生命周期超短，其库存管理政策仍在探索阶段[4]。实际上，若能准确预测医院、血液中心的血液需求量，不但能降低成本，减少用血浪费，减少血液的过量储存，还能根据需求，制定血液产品的采购计划、血液征集计划、生产计划，因此，准确的需求预测是所有供应链规划的基础，它会影响运营计划、产能、运输和库存水平；它可以在保持所需服务水平的同时减少剩余库存，而在该方面的研究却相对匮乏[5]。近年来，机器学习方法发展迅速，并在短期交通流、客流量预测中显示出了较好的效果，且也广泛运用到血液管理的相关研究。如Bhardwaj等[6]运用朴素贝叶斯法、决策树J48、随机树、K-均值聚类等算法将血液捐赠者的信息从大数据集中分类，预测献血者的献血行为。Beline等[7]运用监督的机器学习方法准确预测了重症监护室患者中央导管相关血流感染状况。

因此，本文结合机器学习方法预测血液中心的血小板日均需求量，提出了集成经验模态分析(Empirical Mode Decomposition，EMD)与长短期记忆神经网络(Long Short-Term Memory，LSTM)的血小板需求预测方法，并在输入变量中融合了天气状态，有效提高了预测的准确度。

1 集成EMD方法与LSTM方法

1.1 EMD方法

EMD本质上是将原始数据分解为利用局部特征时间尺度，在原始信号中提取出若干个本征模函数(Intrinsic Mode Function，IMF)分量和1个残余量。其中本征模函数必须满足2个条件：1)函数在整个时间范围内，局部极值点和过零点的数目必须相等，或最多相差1个；2)在任意时刻点，局部最大值的包络(上包络线)和局部最小值的包络(下包络线)平均必须为0[8]。

EMD的分解过程可以描述为[8]：

Step1：对于一个给定的时间序列x(t)，找出x(t)的所有极值点，设本征模函数的总数为i，并令i=1；

Step2：用插值法对极小值点形成下包络emin(t)，对极大值点形成上包络emax(t)；

Step4：计算原始数列x(t)与均值mi(t)的差，得到新的数列hi(t)=x(t)-mi(t)；

Step5：检验数列hi(t)是否满足本征模函数的2个条件：

Step5.1：若满足，则hi(t)为第i个IMF，记为ci(t)，并计算残余分量ri(t)=x(t)-hi(t)；

Step5.2：若不满足，则用hi(t)替代原始数列hi(t)，返回Step1，i=i+1；

通过上述过程，x(t)被分解为n个IMFs和1个残余分量rn(t)之和。

(1)

式中：IMFsc1(t)，…，cn(t)表示从高频(短周期)到低频(长周期)的分量；rn(t)表示原始数据x(t)的一般趋势。

1.2 LSTM模型

循环神经网络(Recurrent Neural Network，RNN)可以视为1个普通的网络做了多次复制后叠加在一起组成的。每1个网络会把它的输出传递到下1个网络中(见图1)。RNN虽然适合非线性时间序列的建模，但存在梯度消失和爆炸的问题，不能很好地拟合滞后时间步很长的时间序列。而LSTM神经网络是RNN的扩展，能有效克服梯度消失与爆炸问题[9]。

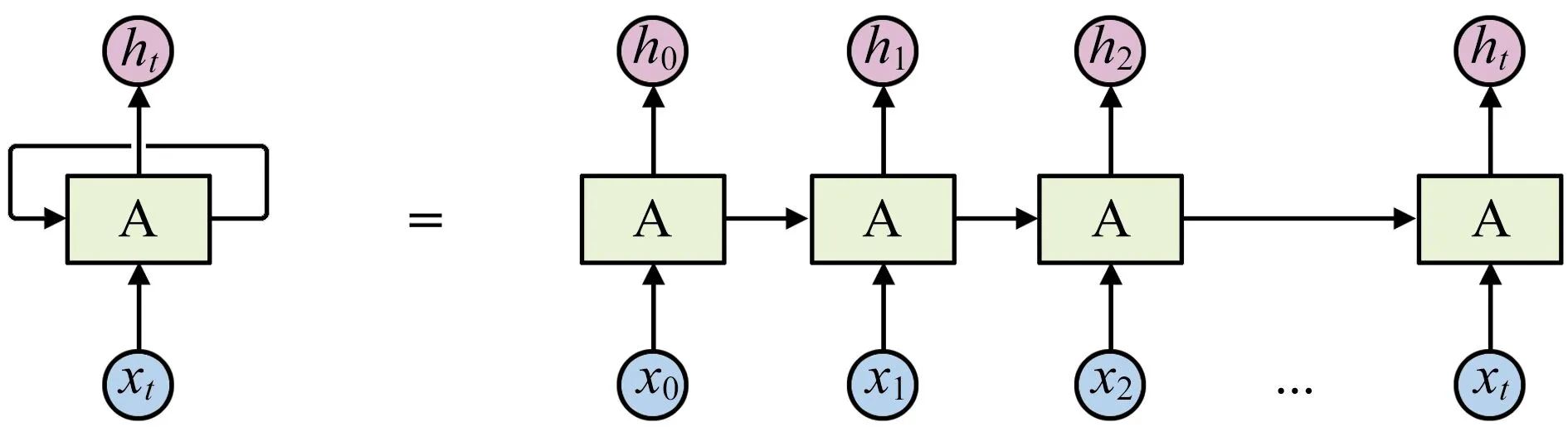
图1 RNN的结构图

LSTM最关键的地方在于cell(整个绿色的框就是一个cell)的状态和结构图上面的那条横穿的水平线(见图2)。每个LSTM有3个这样的门结构，来实现保护和控制信息，分别为遗忘门、传入门与输出门。

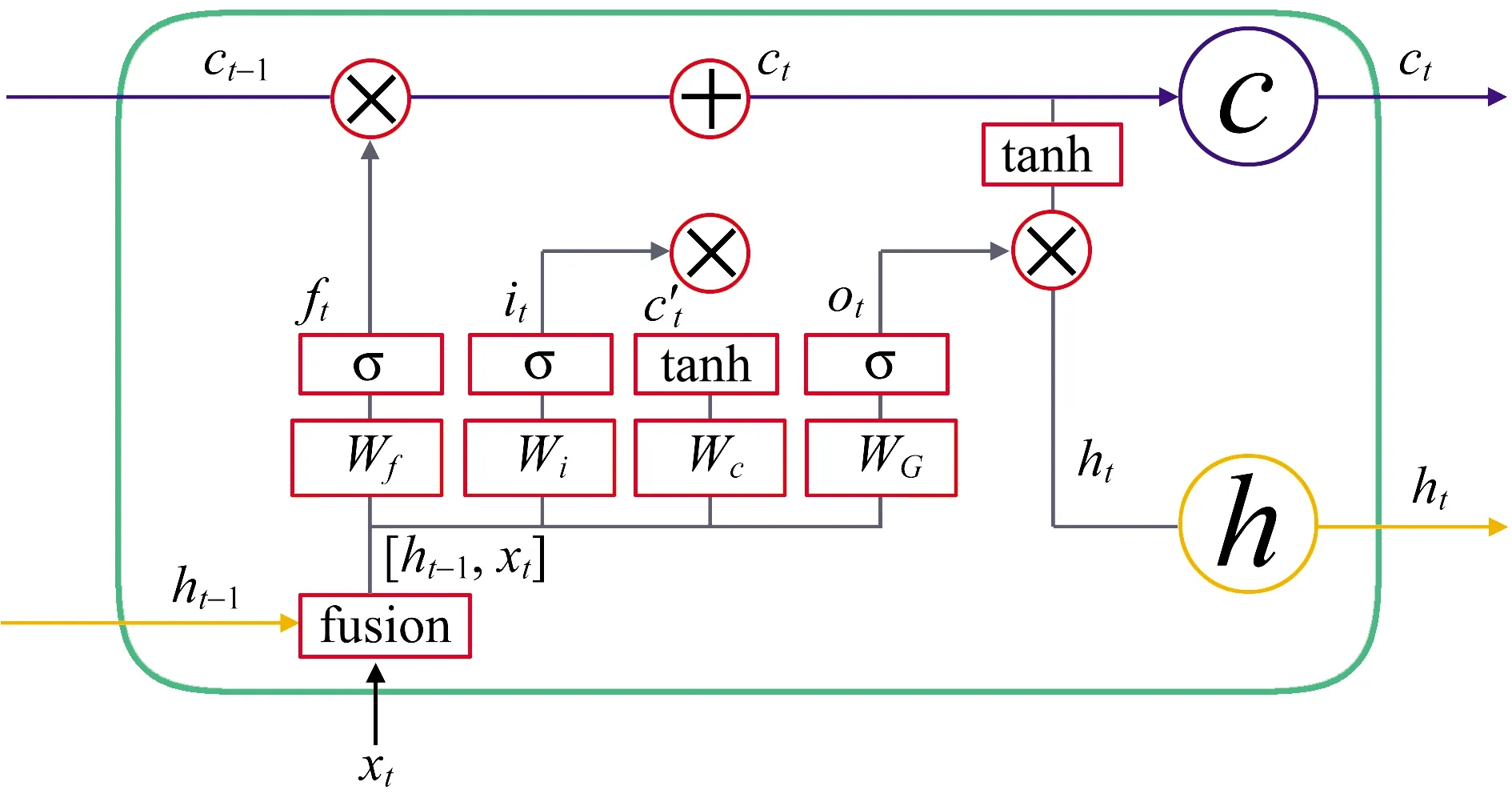
图2 LSTM图内部结构

遗忘门决定删除当前cell中的那些信息，其激活值ft可以表示为：

ft=sigmoid(wfxxt+wfhht-1+bf)。

(2)

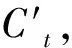
(3)

it=sigmoid(wixxt+wihht-1+bi)。

(4)

式中：wcx，wch，wix，wih为权重；bC，bf为偏差值；tanh=(ex-e-x)/(ex+e-x)。

通过训练样本，使得损失函数最小化确定LSTM模型的权重与偏差值。损失函数度量的是预测值与真实值之间的差异，可以是均方差Ems、平均绝对误差Ema、平均绝对百分比误差Emap等，一般选用Ema。LSTM神经网络采用Adam优化算法进行训练。因为ADAM优化算法具有计算效率高、实现简单、内存需求低、对梯度对角缩放不变性等优点[9]。

2 案例分析

2.1 数据准备

将所提出的短期交通预测模型应用于成都市血液中心采集的数据进行分析，该血液中心为成都市120多家医院和储血点提供供血服务(含郊县)。将2014年1月1日—2017年7月2日的血小板日需求量作为原始数据集。由于血小板有A、B、AB及O型几种类型，O型血小板是万能血小板，本文仅考虑O型血小板，本文方法同样适用于其他类型的血小板需求预测。将原始数据集分为2个子集：前80%的数据作为训练数据集，其余数据作为测试数据集[10]。血液需求预测模型一般运用均方根误差Erma、平均绝对百分比误差Emap评价其性能[5]。

(5)

(6)

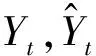
2.2 IMF抽取

运用Python 2.7中的pyhht包实施EMD方法，将原始数据分解为6个本征模态IMF与1个趋势项res.，IMF1，…，IMF6平均周期(频率)由短(高)变到长(低)，表现出明显的多尺度特征(见图3)。前几个高频的分量代表原始数据中的高时变或噪声，后几个分量代表长周期部分。表1是相关系数与方差贡献，由表1可知，IMF2、IMF3与原始数据有较强的正相关性，其中pearson相关系数分别为0.437，0.524。根据kendall相关系数，IMF2、IMF3与原始数据的相关性较高，分别为0.304，0.373，与pearson相关系数一致。IMF3的方差贡献比最大，对血小板需求影响最大，IMF6的影响最小，IMF1～IMF5为血小板需求的有效组成部分，其最小周期为1.2 d，最大周期为11.8 d，显示出了血小板需求短期波动性明显。

图3 EMD分解结果

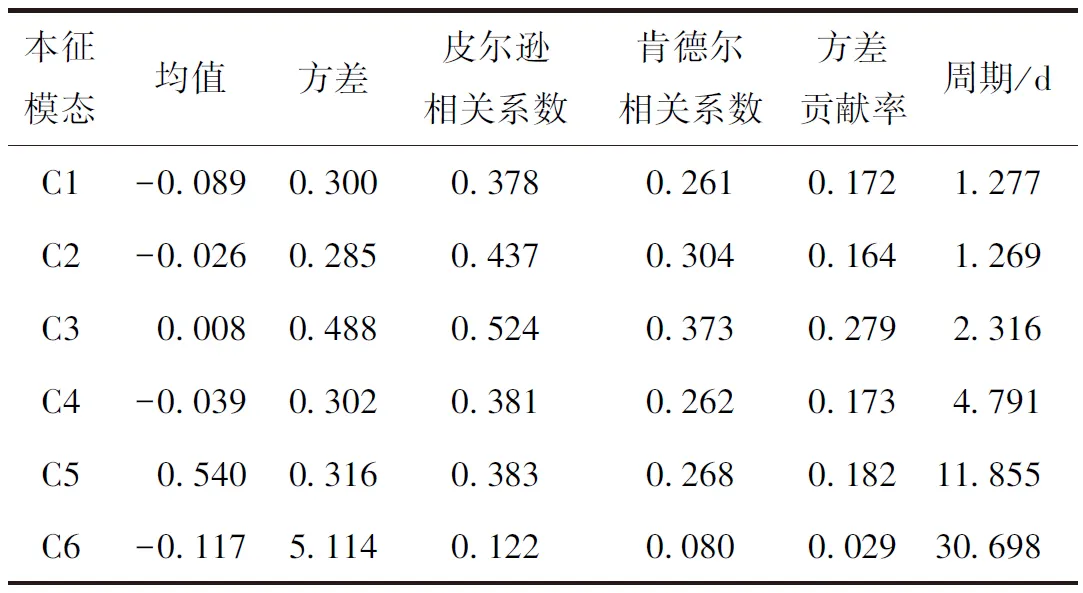
表1 相关系数与方差贡献率

2.3 实验设计

为了更好地检验EMD+LSTM方法的相对预测性能，本文分别采用了差分自回归移动平均模型(Autoregressive Integrated Moving Average Model，ARIMA)、RNN、随机森林(Random Forest，RF)、极端随机森林(Extremely Random Forest，ERF)、梯度提升(Gradient Boosting Decision Tree，GBDT)等5种方法进行对比实验。所有实验均在Win7平台下，采用Python 2.7中的Theano+Keras包。

2.3.1 LSTM参数灵敏度分析

由文献[9]可知，为了优化模型结构，提高预测性能，通过灵敏度分析方法优化LSTM神经网络参数，包括迭代次数、批量大小、节点数。通过灵敏度分析方法设置迭代次数为20，批量大小为10，节点数为15。

2.3.2 结果分析

以原始数据为输入变量，分别运用ARIMA、RNN、LSTM模型测试案例。首先对原始数据进行单位根检验(ADF)[5]，ADF结果为-5.754，小于1%临界水平，拒绝原假设；另外，P也非常接近于0，故原始数据是平稳的(见表2)。ARIMA(p，d，q)模型，原始数据是平稳的，则d=0，p，q在1，…，5之间任意取值，以赤池信息量准则(Akaike Information Criterion，AIC)最小为目标，确定ARIMA模型的参数。RNN、LSTM模型滞后时间步为1。根据表3，RNN、LSTM的Erms分别比ARIMA减少了19.711%与27.686%，Emap分别减少23.867%与31.813%，故RNN、LSTM的预测效果明显优于ARIMA，LSTM略优于RNN。其结果表明，对于非线性数据的预测问题，神经网络RNN、LSTM的预测效果优于传统的时间序列ARIMA模型，LSTM略胜于RNN神经网络。在机器学习方法中，BF因其高效的性能常被用作基准模型，而GBDT在处理非线性数据问题方面具有较好的优势[11]。因此，以原始数据、所有IMF向量及res.为输入变量，分别运用RF、ERF、GBDT与LSTM模型测算案例，所有模型的滞后时间步为1。表4显示了实验结果，BF、ERF、GBDT的Erms与Emap均相差不大，相比BF、ERF、GBDT，LSTM的Erms至少减少了2.361%，Emap减少15.358%，因此，相比其他机器学习方法，LSTM在时间序列预测中具有较好的效果(见表5)。

表2 单位根检验

表3 ARIMA、RNN、LSTM试验结果

表4 ELSTMn测试结果

表5 EMD与RF、ERF、GBDT与LSTM组合方法测试结果

考虑滞后时间步对预测准确性的影响，设置LSTM的滞后时间步分别为2、4、7、12，以原始数据、IMF、res.为输入变量测试案例，为了表述方便，用ELSTMn表示滞后时间步为n的EMD+LSTM模型。根据表4，所有的Erms、Emap均小于ELSTM1，其中，ELSTM2最小，Erms、Emap分别比ELSTM1减少5.892%与13.355%。血液需求影响因素众多，如人口状况、气候等因素，在输入变量中增加相关因素又可能提高预测模型的准确率[12]，但是，相关数据收集比较困难。本节在输入变量中增加天气状态，在不同滞后时间步下测试ELSTMn，用ELSTMn+表示滞后时间步为n的EMD+LSTM+天气状态模型，其中天气状态用0-1变量表示，测试结果见表6，Erms最少降低31.687%，平均降低34.765%；Emap最少降低12.709%，平均降低16.620%，其中ELSTM12+的Erms、Emap均最小，结果表明，天气状态影响血小板需求量，增加天气状态影响能有效提高预测模型的准确性。

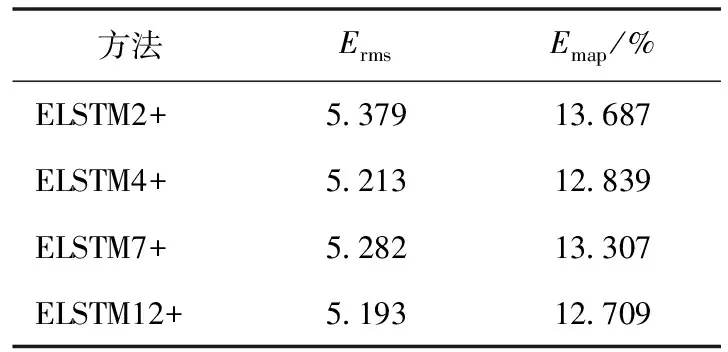
表6 ELSTMn+测试结果

3 结语

本文提出了一种混合EMD-LSTM模型进行血小板的短期需求预测，并得出以下结论：

1)综合经验模态分解方法揭示了短期O型血小板需求的波动特征是由不同振荡尺度的波混合叠加而成，通过数据预处理来提取隐含在数据中的有意义的模式或特征，可以极大提高预测模型的预测能力。

2)相对于其他机器学习方法，LSTM更适应于具有非线性关系的血小板需求问题。

3)EMD+LSTM的混合方法能够有效提高预测的准确性，相比于1个滞后时间步，多个滞后时间步的预测效果更佳，说明血小板需求量不是马尔科夫链。同时，天气因素(即天气状态，雨、晴等)会影响预测模型的准确性。

本文在输入变量中仅考虑了天气因素对血小板需求量的影响，其他因素如经济发展水平、人口数量增长等因素是否影响预测模型的准确性，今后还要进一步研究。