基于期望最大化的局部扩展移动立体匹配算法

2022-12-21周武威刘子濠谭书伦郭龙源胡建斌

成都工业学院学报 2022年4期

周武威，刘子濠，王琼，谭书伦，郭龙源，胡建斌

(1.湖南理工学院 a.信息科学与工程学院; b.机械工程学院; c.机器视觉与人工智能研究中心，湖南岳阳 414006；2.广西中烟工业有限责任公司,广西桂林 530000)

立体匹配在无人驾驶[1]、三维重建[2]、虚拟现实[3]等领域有着广泛的应用。研究者提出了很多有效的立体匹配算法。基于扩展移动的算法是目前的研究方向之一。Boykov等[4]首先提出了扩展移动来求解立体匹配问题，扩展移动能同时改变大部分像素的标签，很好地克服了陷入局部最小值的问题。针对扩展移动建模过程繁琐的问题，Kolmogorov等[5]给出了一种通用的建模方法，简化了扩展移动的建模过程。Li等[6]提出了一种多层超像素结构，利用该结构可以在无穷大的三维标签集中进行高效地扩展移动。Taniai等[7]进一步提出了局部扩展移动的方法，该方法通过局部化和空间传播2种方式，并有效结合了倾斜块匹配项[8]和曲率平滑项[9]，具有局部最优、适合并行化和基于导引滤波加速代价计算等优点。但以上算法在弱纹理区域的匹配效果欠佳。

Li等[10]提出了一种基于期望最大化[11]的方法，通过估计扩展移动立体匹配算法的参数，改善了在弱纹理区域的匹配效果。受文献[10]的启发，本文提出了一种基于期望最大化的局部扩展移动立体匹配算法，算法的创新点为：提出了倾斜块匹配项和曲率平滑项的概率模型；基于期望最大化算法自适应地设置局部扩展移动算法的平滑权重。

1 概率模型

首先介绍局部扩展移动立体匹配的费用函数，然后建立费用函数中倾斜块匹配项和曲率平滑项的概率模型，并且基于期望最大化算法分别估计2个概率模型的参数。

1.1 局部扩展移动立体匹配的费用函数

对于左图像I={i}和右图像J={j}(本文将左图像作为参考图像)，根据局部扩展移动立体匹配[7]的费用函数式(1)，可以得到参考图像中像素的视差平面fi=(ai，bi，ci)。

(1)

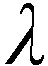
di=aix+biy+ci。

(2)

倾斜块匹配项φi(fi)的定义为：

(3)

ρ(s|fi)=min(CCNN(s，s′)，τCNN)。

(4)

函数CCNN(s，s′)[12]利用卷积神经网络计算分别以s=(xs，ys)和s′=(xs，ys)-(aixs+biys+ci，0)为中心点的2个图像块之间的相似性，τCNN是常数，Wi是以i为中心的窗口，权重ωis实现了基于导引滤波[13]的自适应支持窗口[14]，权重ωis的定义见文献[7]。

曲率平滑项ψij(fi，fj)的定义为：

ψij(fi，fj)=max(wij，

(5)

(6)

di(fj)=ajxi+bjyi+cj。

(7)

1.2 倾斜块匹配项的概率模型

1.2.1 建立概率模型

首先令：

(8)

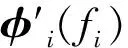
(9)

式中：μ是指数分布的参数；R是均匀分布的参数。定义混合概率：

P(γi=1)=α，P(γi=0)=α′=1-α。

(10)

式中：α是在左图和右图中均可见的像素的比例。对γi求和得到如下边缘概率：

(11)

1.2.2 基于期望最大化算法估计模型参数

给定参考图像中像素的视差平面{fi}，根据期望最大化算法，首先计算：

(12)

然后计算γi的条件概率：

(13)

接着计算对数概率的期望：

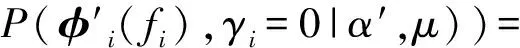
(14)

(15)

(16)

通过最大化式(14)可以得到α和μ的估计值。分别令式(14)对α和对μ的偏导为零，得式(15)和(16)，式(15)中的|I|为参考图像的像素个数。

1.3 曲率平滑项的概率模型

1.3.1 建立概率模型

为参考图像中的每个相邻像素对g设置一个隐随机变量θg，变量的值为2时表示相邻像素对g是共面的，变量的值为1时表示像素对g是连续的，变量的值为0时表示g是不连续的。

为了简化表达，令ψg(fg)=ψij(fi，fj)。曲率平滑项ψg(fg)的定义如下：

P(ψg(fg))=

(17)

式中：ν是指数分布的参数；L是均匀分布的参数；函数δ(ψg(fg))服从狄拉克分布，

(18)

(19)

定义如下混合概率：

P(θg=2)=β;P(θg=1)=β′;

P(θg=0)=β″=1-β-β′。

(20)

式中：β是共面像素对的比例；β′是连续像素对的比例；β″是不连续像素对的比例。

关于θg求和得如下边缘概率：

P(ψg(fg))=

(21)

1.3.2 基于期望最大化算法估计模型参数

给定参考图像中像素的视差平面{fi}，根据期望最大化算法，首先计算：

(22)

式中：g′为连续或不连续的相邻像素对。然后计算θg′的条件概率：

pg′≜P(θg′=1|ψg′(fg′)，β′，ν)=

(23)

接着计算对数概率的期望：

Eg′[logP(ψg′(fg′)，θg′|β′，ν)]=

(1-pg′)logP(ψg′(fg′)，θg′=0|β′，ν))。

(24)

通过最大化这个期望可以得到β′和ν的估计值，分别令式(24)对β′和对ν的偏导为零，得：

(25)

(26)

式中：G′为全体g′组成的集合；|G′|为g′的个数。

2 算法描述

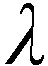
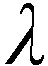
(27)

图1 本文算法流程

3 实验

3.1 实验环境

本文基于计算机视觉开源库OpenCV和局部扩展移动立体匹配算法的开源代码实现所提算法，在Middlebury数据集[15]上进行实验。Middlebury数据集是一个室内场景数据集，它的大部分算法采用原始图像一半分辨率的图像进行计算，本文也采用半分辨率图像。实验用计算机的CPU为Ryzen7 2700主频3.2 GHz，内存为16 GB。

3.2 参数设置

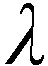
3.3 Middlebury数据集上的在线评测结果

Middlbury数据集有多种评价标准，比如bad 2.0 nonocc标准和bad 4.0 nonocc标准。bad 2.0 nonocc标准下的误匹配率，其含义是最终视差图的非遮挡区域中，与真实视差的绝对差值大于2.0的像素的百分比。类似地，bad 4.0 nonocc标准下的误匹配率，其含义是最终视差图的非遮挡区域中，与真实视差的绝对差值大于4.0的像素的百分比。

本文算法的结果上传至Middlbury在线评测网站后，部分图像对在bad 2.0 nonocc标准下的误匹配率和在bad 4.0 nonocc标准下的误匹配率分别见表1和表2，本文算法的运行时间见表3。

如表1所示，相比于局部扩展移动立体匹配算法，本文算法在bad 2.0 nonocc标准下的误匹配率减少了1%左右。如表2所示，对于图像对Piano，本文算法在bad 4.0 nonocc标准下的误匹配率减少了2.74%，对于图像对PianoL和Playrm，本文算法在bad 4.0 nonocc标准下的误匹配率减少了1%左右，对于图像对Shelves和Vintge，本文算法在bad 4.0 nonocc标准下的误匹配率仅减少了约0.03%，几乎没有变化。