低速流动下的双层中空板强化蓄热研究

任德志，张皓男，宫元娟，王国峰,2

（1.沈阳农业大学a.工程学院，b.信息与电气工程学院，沈阳 110161;2.沈阳工程学院能源与动力学院，沈阳 110136）

日光温室因其具有良好的保温蓄热和透光性能而被广泛应用，越来越多的研究者对日光温室的蓄热保温性能展开了研究，其研究主要集中在新型蓄热结构的设计、充分利用太阳能以及强化水循环换热等方向[1-3]。ATTAR等[4-5]使用以太阳能为热源的水幕换热系统对温室温度进行调节，该方法利用了水的对流传热和导热特性，吸收了太阳的辐射能量，达到了换热目的；徐微微等[6]设计了中空板水循环太阳能集放热系统，考虑了太阳辐射和内部环境换热对夹层水温的影响；马承伟等[7]研究钢管屋架管网水循环集放热系统，测试该系统的集热与蓄放热状况，考虑复杂结构对换热的影响。研究表明，采用带夹层的复杂中空板结构，利用水流吸收太阳能辐射热量对温室进行蓄热已被广泛采用，但现有方法主要是依靠水的对流换热效果进行蓄热，水流的蓄热效率低，提升水流所需能耗大。随着日光温室建造技术的发展以及农作物生长对温室温度要求的限制，日光温室蓄热的需求逐年提升。迫切需要寻求设计先进的换热结构和选择高效的传热技术来满足日光温室的蓄热需求。当水以较低速度流动时，受到黏性的作用水滴会撞击固体表面在壁面产生黏膜。受液滴流动、相间表面张力及壁面黏性力作用，液滴将出现黏着、反弹、扩散、溅射等不同运动趋势，影响水的强化换热作用[8-12]，进而形成液体薄膜流动。液体薄膜流是一种高效的传热传质技术，近年来，国内外研究者逐渐对液膜强化换热理论开展深入研究，ROURKE等[13]基于液膜厚度的源项方程，得到了壁面结构对液膜传热的影响；SEO等[14]采用数值方法，探索了液滴飞溅和扩散现象对液膜换热的影响；刘梅等[15-17]通过改变液体的堆积情况、液膜厚度和壁面结构等因素，提高了水层换热能力。研究表明，液体薄膜流作为一种新型的传热技术方法能够有效地提升蓄热装置的换热能力，其理论已趋于成熟，但实际工业应用案例相对较少，特别是在日光温室蓄热系统研究中并未发现相关报道。

本研究以日光温室的覆盖层为研究对象，设计一款带夹层的双层中空板蓄热系统结构，建立蓄热系统结构的简化模型，并进行传热等效，利用液体薄膜流换热技术，依次研究夹层内完全充满水、夹层内存在气水交界面、水层与底板间存在液体薄膜作用和底面带凸起4种情况的水流换热量。通过对不同模型的传热过程和求解方法的研究，探索在低速水流动下（假设水的流速范围为0.1~0.9m∙s-1）蓄热系统的换热机制，为日光温室蓄热系统的研究提供基础。

1 物理模型

借鉴前人设计的蓄热系统结构，对日光温室的覆盖层进行假想设计，设想一种带夹层的双层中空板蓄热系统结构（图1）。夹层中间有水流通过，水流受重力作用，顺着覆盖层流向地面，流动过程中吸收两侧夹层板的热量，同时吸收太阳辐射热；太阳光照射在夹层顶侧、底侧板和水流上，对夹层板和水流进行加热；夹层板把日光温室、水流和外部环境隔开，夹层板温度受温室内、外部气流流动影响。

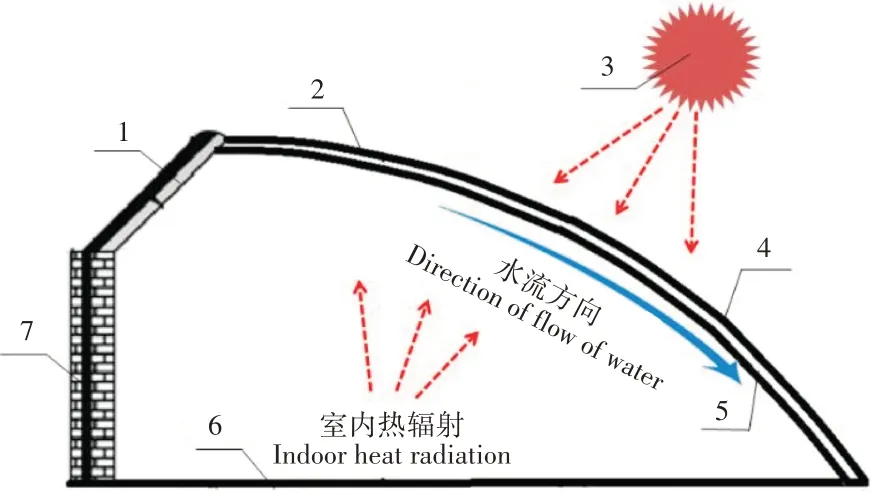
图1 日光温室结构示意图Figure 1 Schematic diagram of solar greenhouse

为了使研究结果具有普遍适用性，本研究对蓄热结构进行等效及简化处理（图2）。假设蓄热结构由两层玻璃板构成，玻璃板夹层中间流过水流，太阳以均匀的辐射强度照射在顶侧玻璃板上（太阳照射时间，6月21日13∶00，照射地点北纬48°、东经123°，天气为晴天），太阳直射辐射强度为862.12W∙m-2，太阳垂直表面散射强度95.52W∙m-2，水平表明散射强度115.52W∙m-2，地面反射强度87.50W∙m-2，底侧玻璃为温室顶棚，直接接触温室内部环境。定义水流动方向为X，阳光直射方向为Y，垂直纸面向外方向为Z，X轴与水平方向夹角θ=15°。选取X方向单位长度1m，Z方向为对称面，顶侧和底侧玻璃板厚度为δout和δin，水流通道的厚度为δw，外部空气温度为T1；内部环境空气温度为T4，水流初始温度为T0；顶部板与水的交界面温度为T2；水与内底板交界面温度为T3，λout、сout、ρout分别为外层玻璃导热系数、比热容和密度，λin、сin、ρin分别为内层玻璃导热系数、比热容和密度，λw、сw、ρw分别为水层导热系数、比热容和密度；h1，h2分别为两层玻璃板表面的对流传热系数，h0为中间水层的对流传热系数。具体数据如表1。

图2 温室水幕简化模型Figure 2 Simplified model of greenhouse water curtain

表1 模型参数Table 1 Parameters of the model

2 换热分析

为了得到液体薄膜流对带夹层的双层中空板蓄热系统结构的强化换热影响，本研究采用逐步深入的研究方法，对4种假设模型进行详细研究。第1种，假设夹层内完全充满水，定义这种情况为全水域模型。全水域模型是一理想模型，可通过理论推导得到精确解，通过与数值解的比较，可以用来验证数值算法的准确性以及网格尺寸的无关性。第2种，在实际情况中，当水以较低速度流动时，夹层内必然会存在气水分离的现象，定义该模型为气水域模型。采用数值方法，在不考虑水的黏性作用情况下，对不同水流速度进行研究，得到蓄热结构的换热量。第3种，假设则是在气水域模型基础上，考虑水的黏性作用，添加液膜源项方程，分析不同水流速度下，液体薄膜流对换热的影响。第4种，最后研究底板布置凸起强化换热筋时，带夹层的双层中空板蓄热系统结构的强化换热性能。

2.1 全水域模型换热分析

利用图2模型对全水域换热模型进行理论推导求解，假设流动为常物性、稳态、无内热源，水流入口初速度V0=0.5m∙s-1，在重力作用下，水流沿斜面流动，太阳辐射换热量δqt。全水域流体换热模型控制方程及其边界条件：

采用流体外掠平板换热理论求解对流传热系数h0、h1和h2，

式中：ν为水的运动黏度[kg·(m·s)-1]。

利用控制方程和边界条件，运用傅里叶公式对全水域换热模型进行求解，全水域模型水流总换热量等于太阳辐射换热量与上、下玻璃板表面换热量之和。

式中：ϕ1、ϕ2为上、下玻璃板表面与环境换热量（W）；ϕ3为太阳辐射换热量（W）；A为接触面积（m2）。

利用CFD软件FLUENT对全水域模型进行求解。网格划分选用六面体结构化网格，在模型各条边和拐角处都进行了网格加密处理和网格无关性验证，以提高计算精度，最终确定网格为268310。在数值求解过程中，采用换热公式ϕ’=сwmΔT计算水流换热量，сw为水的比热容[J·(kg·K)-1]，m为水的流量(kg·s-1)。数值求解所用条件与理论推导所用条件一致。为了能够准确核算数值解与理论解的换热量，将夹层结构模型沿水流的流动方向X划分10等份，分别计算每部分的换热量ϕi，具体理论与数值结果如表2。由表2可知，理论解总换热量为255.67W，数值解总换热量为265.55W，两者相差9.88W，相差3.7%。模型第2~9段，理论解与数值解各段换热量大致相等，其换热量均值为26W，理论解与数值解的最大偏差为0.76W，相差2.9%。数值解的第1段值较大，第10段值较小，这主要是由于第1段是模型的进口段，第10段是模型的出口段，受边界条件影响及计算迭代的影响，数值的差异增加。

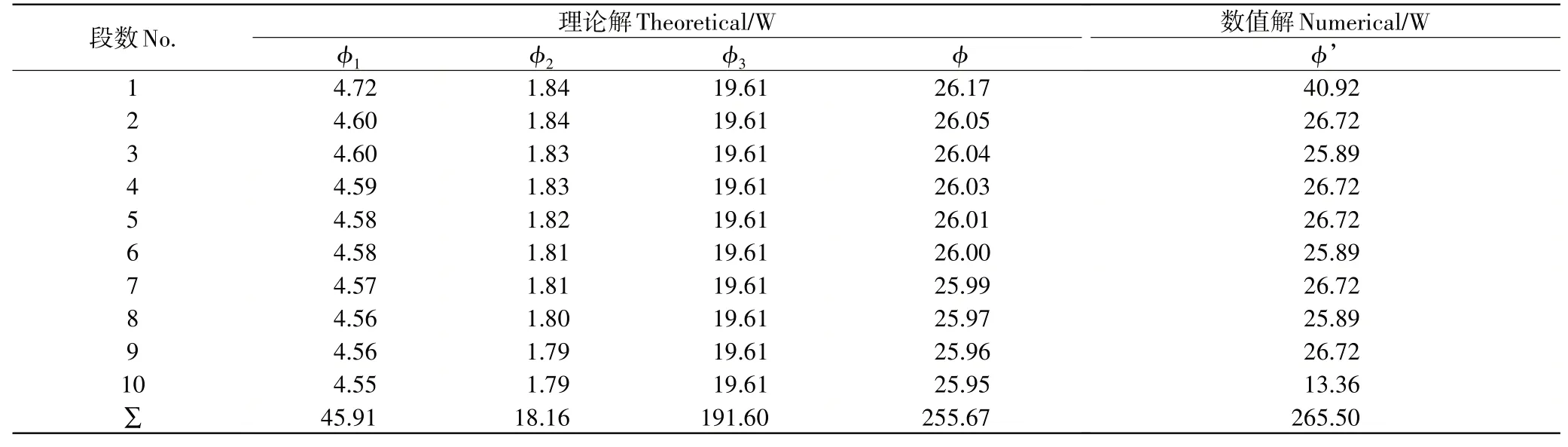
表2 理论解与数值解Table 2 Theoretical and numerical solutions

全水域模型是4个假设模型中唯一可以利用解析推导进行求解的模型，通过理论解和数值解的比对，首先验证了数值计算网格的无关性，其次也为接下来的数值研究提供一定的指导作用。

2.2 气水域模型换热分析

当夹层内水流速度较大时，出口水流温度受质量影响，温升会降低，另外水流质量越高，需要把这部分水提升到屋顶所需的动力就更多，带来的能量消耗也会更多，因此小流量和低流速对夹层内水流的蓄热有利。当水流速度较小时，水流受重力的作用，夹层中间将无法保证完全充满水，必然会出现气水交界的现象，本研究定义这种模型为气水域模型（图3）。

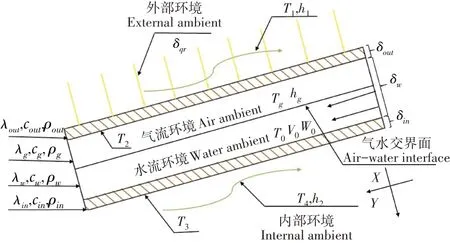
图3 气水域物理模型Figure 3 Physical model of the air-water model

KIM等[1,18]提出以VOF体积力方法计算气水域模型的流动特性与换热特性。该方法不仅考虑夹层板与水流间的热传导关系，还考虑水流与空气层间、水流和夹层板间的对流作用，其控制方程：

式中：αw为水的体积分数；Vw为水流的速度向量(m·s-1)；p为水流的压力(Pa)；μ为水的黏度(m2·s-1)；g为重力加速度的向量(m·s-2)；F为所受外力的向量(N)；Sh为太阳辐射的源项(W)。

采用与全水域模型相同的网格划分方法和换热分析方法，分析模型每段内换热量，具体数值如表3。当进口流速较低时，第2和第3段换热量相对较大；随着流速增加，前两段与后面部分相比换热量逐渐接近，这主要是因为，当流速较低时，受重力作用，水流不能完全铺满模型整个平面（图4），在开始几段，水流接触面积大，流速低，换热时间长，水流温度增加的多，因此换热量高，随着重力作用，水流产生聚集现象，流速增加，换热时间变短，换热量变小。当水流速度比较大时，水流铺满底面，各段的换热量趋于均匀。由表3可得，当V0=0.3m∙s-1时，水流的总换热量为80.17W，当V0=0.9m∙s-1时，水流的总换热量为30.07W，水流换热量相差50.1W。

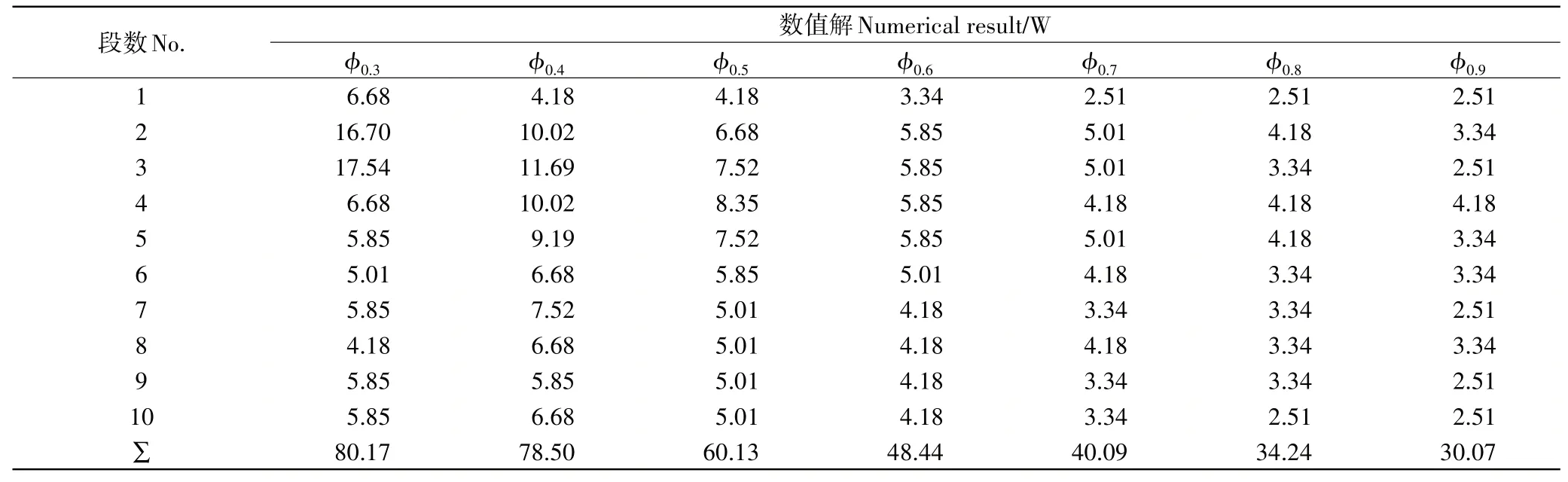
表3 气水域换热值数值解Table 3 Numerical solution of heat transfer value in gas-water calculation domain

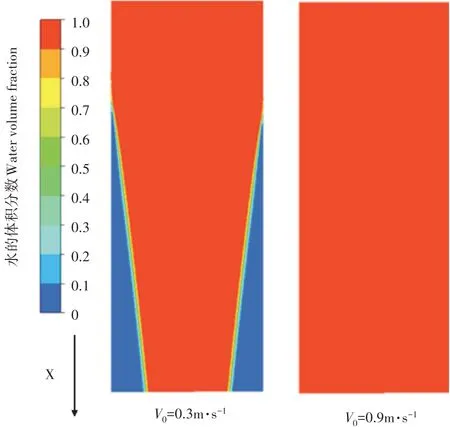
图4 气水域底面水体积分数分布图Figure 4 The distribution diagram of the volume fraction of the bottom water in the air-water calculation domain

在模型出口，沿Y方向，从底板到顶板做一条直线，分析水流速度为0.3，0.5，0.9m∙s-1时，水的体积分数和夹层内水流（或气流）温度与夹层位置的关系。由图5可知，水的体积分数为1时，该点处全部充满水（Ⅰ区）；水的体积分数为0时，该点处充满空气（Ⅲ区）；当水的体积分数为0~1之间时，为水和空气的混合区域（Ⅱ区）。从水的体积分数曲线可知，当水流速度增加时，体积分数对应的水流厚度（夹层厚度）增大，这说明，水流速度越大，水层越厚。水流速度越小，夹层内将呈现气水分离的流动现象。从温度曲线可知，水流速度越小，夹层内的空气温度越高，这说明，当水流速度较小的情况下，顶层气体被太阳光加热的效果越强，空气的温升会越高，夹层蓄热结构的顶层温度T2会越高，越利于蓄热情况的发生。

图5 水层厚度与体积分数和温度的关系Figure 5 The relationship between water layer thickness,volume fraction and temperature

通过对气水模型的研究，可得到低速流动下夹层蓄热结构的换热量以及不同水流速度对换热的影响，为接下来的液体薄膜流提供对比数据。

2.3 液体薄膜流换热分析

在气水模型基础上，考虑水的黏性作用，假设所选速度能够使水流在底板上的流动形成液体薄膜，基于液膜厚度增加源项方程[19-21]，采用用户自定义方程（UDS）方法，在气水模型中引入ROURKE[13]关于液膜厚度的源项方程，求解液膜厚度对传热的影响，分析具有液膜影响条件下夹层蓄热系统结构的换热性能。液膜厚度的源项方程：

式中：H为液膜厚度(m)；∇为表面梯度算子；Vw为水流的速度向量(m·s-1)；mw为质量源量(kg·s-1)；Ts为气水交界面温度(K)；PL为计算域的总压力(Pa)；Tf为平均膜温(K)；pimp、qimp分别为水珠撞击到壁面所引起的动量和能量源项(W·m-3)。

采用相同的分析方法得到夹层结构每段内换热量，具体数值如表4。比较液膜模型与气水域模型的总体换热量可发现，由于在计算过程中增加了液膜源项，液膜模型的总换热量高于气水域模型的总换热量。这说明如果实际模型中存在液膜影响，将会增加夹层蓄热结构的强化换热能力。表3与表4数据所呈现的趋势基本相同，在低速流动的第2和第3段内换热量较大，其他段换热量较为均匀，这说明液膜模型并没有完全改变水流的流动特性，仅增大了该段的换热能力。由表4可知，当V0=0.3m∙s-1时，其换热量为105.2W，当V0=0.9m∙s-1时，其换热量为40.92W，水流速度增加，会削弱液膜影响，液膜的强化换热效率降低。

表4 基于液膜作用的气水域换热值数值解Table 4 Numerical solution of heat transfer value in air-water calculation domain based on thin film effect

图6为气水域模型与液体薄膜流水流速度的对比关系。由图6可知，液体薄膜流出口水流温度要高于气水域模型，当进口速度较小（V0=0.3m∙s-1）时，此时水流出口温度为283.355K，在1m的流动范围内，两者相差0.083℃。

图6 液膜作用对温度的影响Figure 6 Effect of thin water film on temperature

2.4 圆柱凸台阵列强化换热分析

本研究在液体薄膜流基础上，引入肋化强化换热，在夹层内增加圆柱凸台，圆柱凸台的布置形式如图7，沿水流方向把模型分成3个区域，分别是圆柱凸台阵列上游区，L1=200mm；圆柱凸台阵列区，L2=500mm；圆柱凸台阵列下游区，L3=300mm；圆柱凸台高度δ=3mm；凸台圆心的横向间P为80mm，纵向间距S为100mm，底圆直径D分别为50mm。

图7 圆柱凸台阵列模型Figure 7 Cylindrical boss array model

图8为液体薄膜与圆柱凸台阵列模型的对比关系。由图8可知，水流出口温度随入口速度增大而降低，但二者受初速度改变影响程度不同，液体薄膜模型受初速度影响缓慢；圆柱凸台阵列模型受速度的影响变化范围大。通过对比二者的出口温差发现，圆柱凸台阵列模型出口温差是要远高于液体薄膜模型，当V0=0.3m∙s-1，此时水流出口温度为283.96K，水层换热量为415.66W，两者温差最大，为0.605℃，其水流温度变化远大于液体薄膜模型。

图8 圆柱凸台阵列对出口温度的影响图Figure 8 Effect of cylindrical boss array on exit temperature

进一步对低速水流进行分析发现，水流在低速流动时，水流与圆柱凸台壁面产生黏性剪切力，减小水层向下速度，增长换热时间，同时因凸台扰流作用，水流铺满整个底面，加大换热面积，增强水流换热。图9为底面水的体积分数分布图，由图9可知，当V0=0.3m∙s-1时，底面完全被水流铺满，水的体积分数介于气水交界状态，说明水层较薄，底面与顶层空气间的换热容易被穿透，结合气水域研究可知，当水流速度小时，顶层空气温度高，这会使得水层温度梯度更大，增强整体水层换热能力。当V0=0.6m∙s-1时，底面上几乎完全被水层铺满，说明水层厚度越大，传热性将变差。

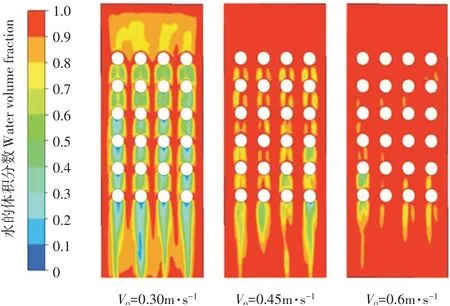
图9 底面水流体积分数Figure 9 Water volume fraction at bottom surface

图10为底面温度分布图，由图10可知，水流进入圆柱阵列区，水流温度逐步提升，当水流速度小时，水流温度提升快。与图9对照还可发现，水流体积分数越低，水流温度就会越高，这说明，较薄水流易于热量吸收，对水流温度的提升有益。

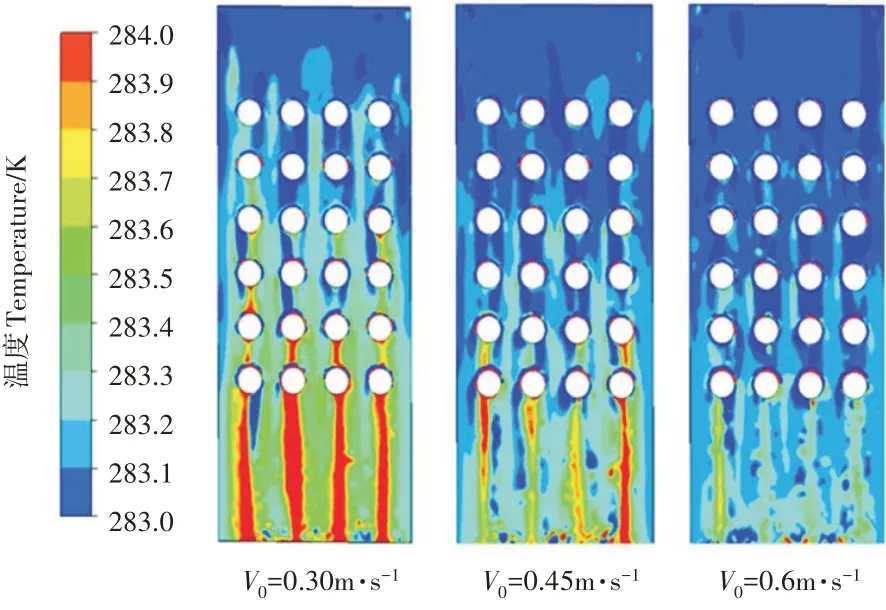
图10 底面温度分布图Figure10 Temperature distribution at bottom surface

3 讨论与结论

随着工业、农业迅速发展，能源短缺问题愈发凸显，能源高效利用和强化换热研究越来越被众多学者重视。液膜换热作为一种高效的强化换热方式，不仅可以强化流体换热效果，还因流量小、热流密度高、传热介质方便易得等优势受到广泛关注。FRIEDRICH等[22]在研究液膜换热的影响时，提出将液膜厚度的源项方程运用在气液两相流换热研究中，用于解决气液两相交接面的热传递问题以及低速黏性流体的流动对壁面换热的影响。JAYANTI等[23]采用数值模拟的方法，探究液膜厚度与传热系数的关系，并验证了在低流速流动时，流体在液膜作用下强化换热能力逐步增强。

本研究结果表明，基于黏性流体液膜换热理论和非平整基底的强化换热理论的低速流动下的双层中空板强化蓄热结构是一种高效的强化换热结构，有利用水流热量的收集。通过对气水域模型的研究，可得到无液膜源项方程条件下带夹层的双层中空板蓄热系统结构的总换热量。同时得到当水流速度较小时，水层的厚度变化以及夹层内水（气）的温度变化。结果表明，当水流速度在0.3~0.9m∙s-1区间内，水流速度越小，夹层内水层越薄，水流换热量越大，水流出口温度越高。在双层中空板结构内形成的液体薄膜流可增强蓄热系统的换热能力。液体薄膜流与气水模型的流动特性是一致的，但由于液膜厚度的作用，传热效果被增强，当水流速度越小时，其强化换热效果越强。圆柱凸台的强化换热结构可进一步增强液体薄膜流换热效果。当水流速度较小时，液膜流在底侧板面铺设更均匀，液膜厚度更薄，传热效果更好。带圆柱凸台的强化换热结构可用来进一步开展工程应用研究。