关于次可加数列的若干注记
2022-12-21江蔓蔓
◎江蔓蔓
(广州航海学院基础教学部(人文社科部),广东 广州 510725)
1 引言
数列极限的存在性证明是高等数学中的常见问题,也是学生学习过程中的难点.次可加数列是数学中常见的一类数列.本文以次可加数列关于其项数之比的极限存在性问题为例,分析如何利用上下极限与下确界来证明数列极限的存在性.本文的第二部分以泛函分析中线性算子的谱半径以及动力系统中单位圆周的保向自同胚的旋转数这两个概念为例,说明次可加数列在数学中的重要作用.
2 次可加数列的极限性质及其两种证明方法
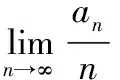

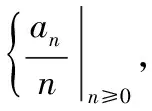

证法一(上下极限):我们固定一个正整数k.
对于任意的正整数n,都存在唯一的整数p,r,使得n=pk+r并且0≤r≤k-1.
不难看出,当n趋于无穷大时,p也趋于无穷大.
令R=max{ai:0≤i≤r-1}.我们有如下关系:
(1)
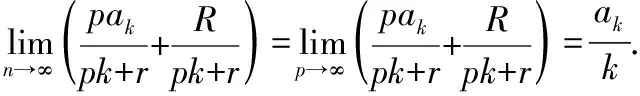
令n→∞,并对不等式(1)的左右两边取上极限可得:
由于k可取为任意正整数,
令k→∞,并对上式左右两边取下极限可得:

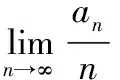
事实上,将n表示成奇偶形式:n=2p+r,其中r∈{0,1}.
因此,我们有如下关系:

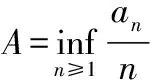


接下来我们考虑A为有限值的情形.根据下确界的定义,对于任意ε,存在正整数k,使得:
(2)
对于任意的正整数n,存在唯一的整数p,r,使得n=pk+r并且0≤r≤k-1.
不难看出,当n趋于无穷大时,p也趋于无穷大.
令R=max{ai:0≤i≤r-1}.我们有如下关系:
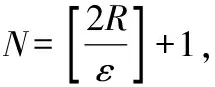

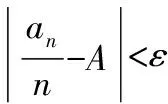

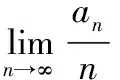
注2:比较上述给出的两种方法:定义法相对于上下极限法的优势在于目标明确,不足之处在于需要事先猜测可能的极限值.在大多数情况下,数列极限值并不明确,也不易猜测.相比之下,上下极限法则不需要猜测极限值.同时,数列的上极限与下极限总是存在的.因此,对于上下极限法,我们所需要的是证明这两者相等.
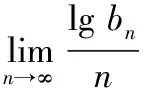
3 应用
次可加现象在数学中非常常见,比如我们熟知的三角不等式(对于平面上任意三点A,B,C,A到C的距离不大于A到B的距离与B到C的距离之和)以及测度的次可加性(可测集A与B之并的测度不大于A的测度与B的测度之和).次可加数列广泛应用于泛函分析、动力系统、遍历论、随机过程等现代数学分支.本文以旋转数与谱半径为例加以说明.
3.1 旋转数
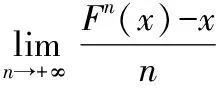
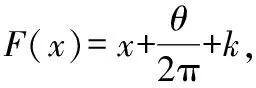
由于F:R1→R1是f:S1→S1的提升映射,因此F(x+1)=F(x)+1.由于f:S1→S1保持定向,因此若x,y∈R1满足x-y≤1,则有F(x)-F(y)≤1.由此可知,若x-y≤k,则Fm(x)-Fm(y)≤k.由递推可知:
Fm(x)-Fm(y)≤k(∀x-y≤k)
(3)
对于所有非负整数m与k都成立.令kn(x)表示Fn(x)-x的整数部分(即不超过Fn(x)-x的最大整数),则Fn(x)-x≤kn(x)+1≤Fn(x)-x+2.从而有:
Fm+n(x)-x=(Fm(Fn(x))-Fm(x))+(Fm(x)-x)
≤kn(x)+1+(Fm(x)-x)
≤(Fn(x)-x)+2+(Fm(x)-x).
因此数列{Fn(x)-x+2}n≥1是次可加数列.
对于任意x,y∈R1,记M为不小于|x-y|的最小整数,
则|x-y|≤M.由(3)式可知|Fn(x)-Fn(y)|≤M对于任意非负整数n都成立.从而:
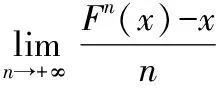



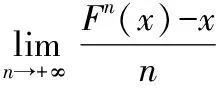
综上,保向自同胚映射f:S1→S1的旋转数是良好定义的.
3.2 谱半径
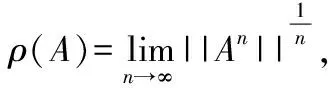
注意到如下关系:
||Am+n||≤||Am||·||An||.

对上式两边取对数可得:
lg||Am+n||≤lg||Am||+lg||An||.
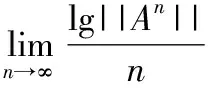

4 结语
次可加数列是数学中非常常见的一类数列,本文从上下极限与下确界两个角度证明了次可加数列关于其项数之比的极限存在性.同时,本文还选取了谱半径与旋转数这两个概念来说明次可加数列的应用,以加深学生对次可加数列的理解.
