基于递归图的两相流流动特性分析与流型识别

张立峰, 王 智

(华北电力大学 自动化系,河北 保定 071003)

1 引 言

两相流流动系统广泛存在于工业生产与日常生活当中,关于气液两相流流动特性的研究对化工生产、石油运输、火力发电等行业的产能优化与产业升级具有重要作用[1～3]。流型是两相流流动的基本特征,实现流型的准确辨识对安全生产以及流动机理研究具有重要意义。过程层析成像技术由于其结构简单、精度高、非辐射等优点受到广泛关注[4,5],基于电阻层析成像技术(electrical resistance tomography,ERT)的流型辨识方法主要有2种:1) 对测量数据进行特征提取,分析不同流型下测量数据的演变规律,进而实现流型辨识;2) 利用图像重建算法实现流型辨识[6,7]。图像重建算法的辨识成功率直接受成像结果影响。相较而言,使用分析测量数据统计特征进行流型辨识结果更为准确,并且可以观察不同流型之间的演变规律,为分析两相流流动机理提供参考。分析测量数据统计特征可从宏观上描述流型演变规律,在损失一定微观特征的前提下仍能保持流型辨识的准确性,且计算量减少,检测实时性增强。文献[8]根据数据特点构造多个标准进行辨识,但这种方法忽略了时序数据的混沌特性。相空间重构技术常被用来分析混沌时间序列的演变规律,文献[9～11]通过重构出的相空间向量搭建复杂网络进行流态分析。递归图可以在二维空间上刻画高维复杂系统运动中的递归行为,经过阈值分割后,可用来分析不同流型的流动特点[12,13],但阈值选择会影响递归率等评价指标的求取,不合理的阈值会影响流型辨识的准确性。

本文通过求取测量数据均值,对均值时间序列进行相空间重构,绘制递归图,求取无阈值递归图图像信息熵来实现流型辨识,并选取合理阈值后分析了不同流型的流动特点。

2 基本原理

2.1 相空间重构

气液两相流流动特性复杂,属于典型的非线性系统,测量得到的数据信号具有混沌特性。进行混沌时间序列分析时,相空间重构技术具有重要意义。Takens提出的嵌入定理[14]表明可以将一维时间序列重构到高维相空间中,进而实现由低维测量数据到高维复杂系统的映射。

对于长度为N的一维时间序列{x(1),x(2),…,x(N)},使用延迟时间τ将其重构到m维相空间:

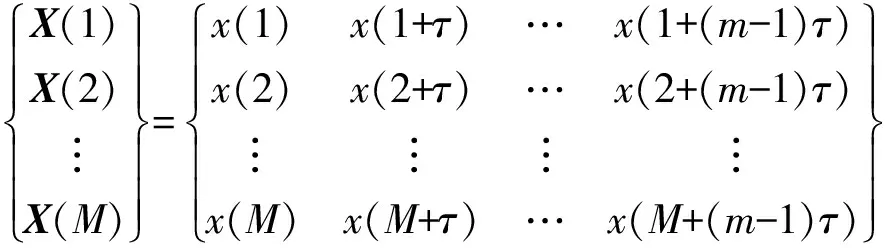
式中M=N-(m-1)τ。

延迟时间τ与嵌入维数m直接关系到能否对原动力学系统实现准确刻画。C-C算法[15]是一种常用的计算m与τ的方法,具有计算量小且结果准确的优点。C-C算法通过求取关联积分,估计出τ和τw(时间窗),进而求得m。C-C算法计算流程为:

定义关联积分函数

C(m,N,r,τ)=

(1)

式中：r>0；Θ为Heaviside函数。令

S(m,N,r,τ)=C(m,N,r,τ)-Cm(1,N,r,τ)

(2)

当N→∞时,可得

(3)

选取半径r,定义差值

ΔS(m,τ)=max{S(m,rk,τ)}-min{S(m,rk,τ)}

(4)

根据统计学理论,取m为范围在[2,5]内的整数;rk=kσ/2,k为范围在[1,4]内的整数,σ为序列标准差。则:

(5)

(6)

(7)

式(5)的第1个零点或式(6)的第1个极小值即为对应的最佳延迟时间τ,式(7)的最小值为时间窗长度τw。

2.2 递归图

递归图可以在二维平面上刻画高维复杂系统运动中的递归行为。对于相空间重构得到的时间序列Xi与Xj,其递归值计算为:

(8)

递归图的纹理结构蕴含原动力学系统中相空间吸引子随时间变化的趋势和规律。通过分析不同流型下递归图的纹理特征,可以揭示两相流流动中复杂的动力学演化行为。

递归图主要包括4种结构:均匀结构、漂移结构、突变结构以及周期结构。均匀结构一般出现在随机系统中;漂移结构是由系统中某些缓慢变化的参数引起的,表现为向左上角以及右下角的渐变行为;周期结构一般出现在震荡系统中,表现为等间距的出现黑块;突变结构由系统中参数的剧烈变化引起,表现为大片的黑块。

2.3 图像信息熵

图像的信息熵[17]可以反映其灰度分布的聚集性。对于任意一幅图像,常用的信息熵计算式为:

(9)

式中:g为图像灰度值;gmax为图像最大灰度值;P(g)为图像中灰度值为g的像素点数与总像素点数之比。

3 实验部分

3.1 实验设备

实验在华北电力大学先进测量实验室的可移动气水两相流实验装置上进行,实验装置示意图如图1所示。

试验段安装16电极ERT阵列传感器,采用相邻激励模式,通过数字化ERT系统将采集的模拟量转换为数字量,从计算机导出测量数据。每次完整扫描,共可获得120个独立测量值。试验中,固定液相流速,逐步增加气相流速,采集5种流型的流动数据,每种流型采集3组,每组数据包含500帧(120帧/s)。图2(a)～图2(e)分别为泡状流型、泡状-弹状过渡流型、弹状流型、段塞流及段塞-混状过渡流型。

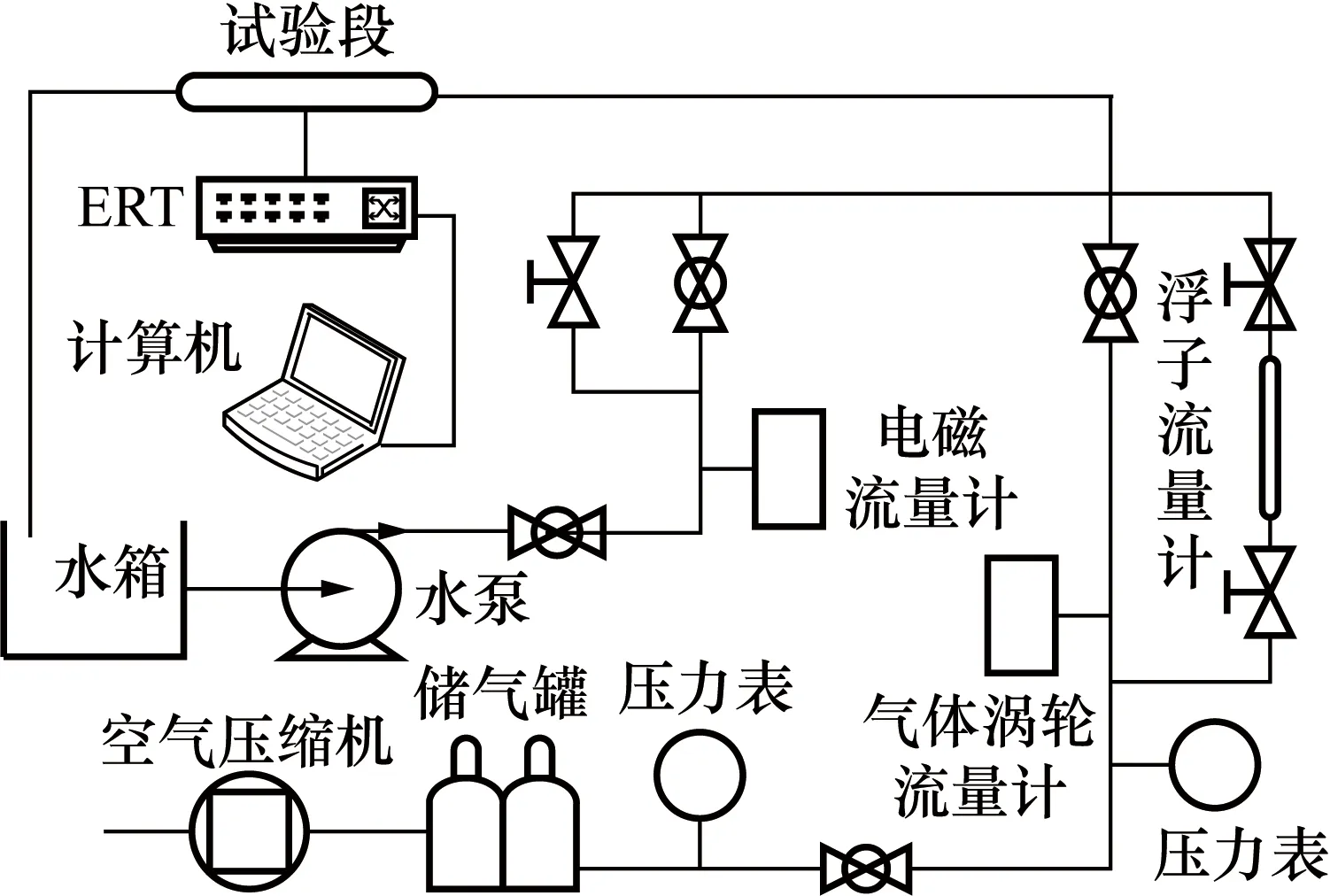
图1 实验装置Fig.1 Experimental device

图2 5种流型图像Fig.2 Flow image

3.2 数据处理

测量得到的120维原始数据维度过高,需提取统计量进行降维处理,从而减少计算量,增加流型辨识的实时性。均值可以反映数据的集中程度,对120维原始数据做预处理,进行线性变换,并求取均值,图3所示为不同流型下均值随帧数变化曲线。

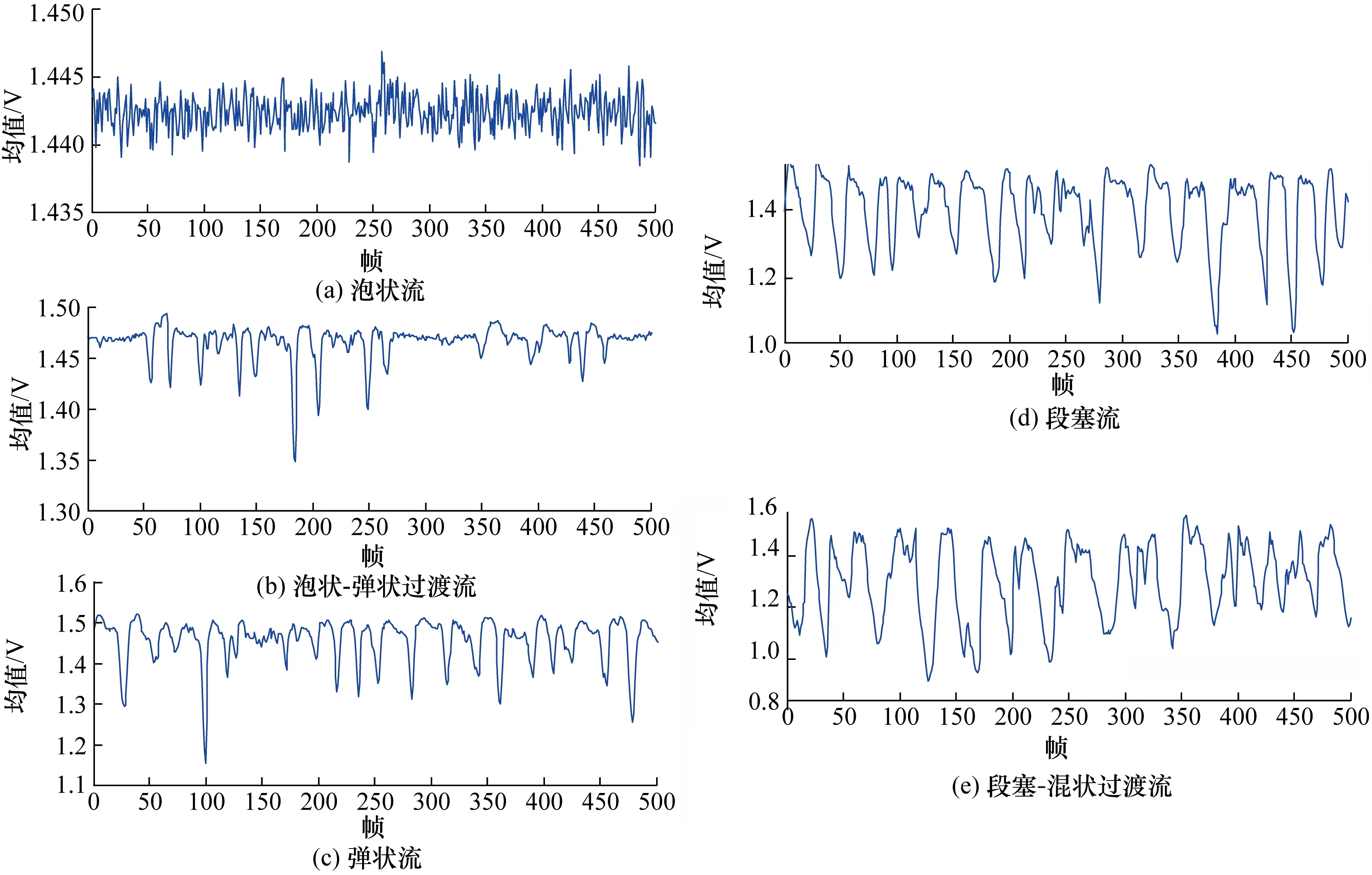
图3 测量数据均值序列Fig.3 Mean series of measurement data

由图2和图3可见,泡状流下系统具有很强的随机性,分散的小气泡还未聚合,使其均值表现为在很小的范围内波动。气泡开始聚合后,大气泡出现会使得均值产生剧烈变化,此时波动幅度在某一点会产生剧变。弹状流下系统的周期性特征可以初步观察到,同时由于气泡进一步聚合,均值波动幅度仍在变大。段塞流时气塞与液塞交替出现,系统的周期性特点比较明显。继续增加气相流速,气塞开始被击碎,流动变得剧烈,系统向混状流过渡,均值波动更加频繁,此时周期性特点未完全消退。

随着流动剧烈程度的增加,系统变得更加混乱,测量数据均值的波动幅度越来越大,并逐渐呈现出一定的周期性变化趋势,段塞流下的气塞被击碎后,系统的周期性趋势开始减弱。均值有效反映了气液两相流流动系统的复杂程度,可以用来辨识流型。

4 结果分析

本文对一维均值时间序列进行相空间重构,进而绘制递归图,选择合理阈值,根据有阈值递归图分析流型的演变规律,对无阈值递归图求取图像信息熵,从而辨识流型,流程如图4所示。

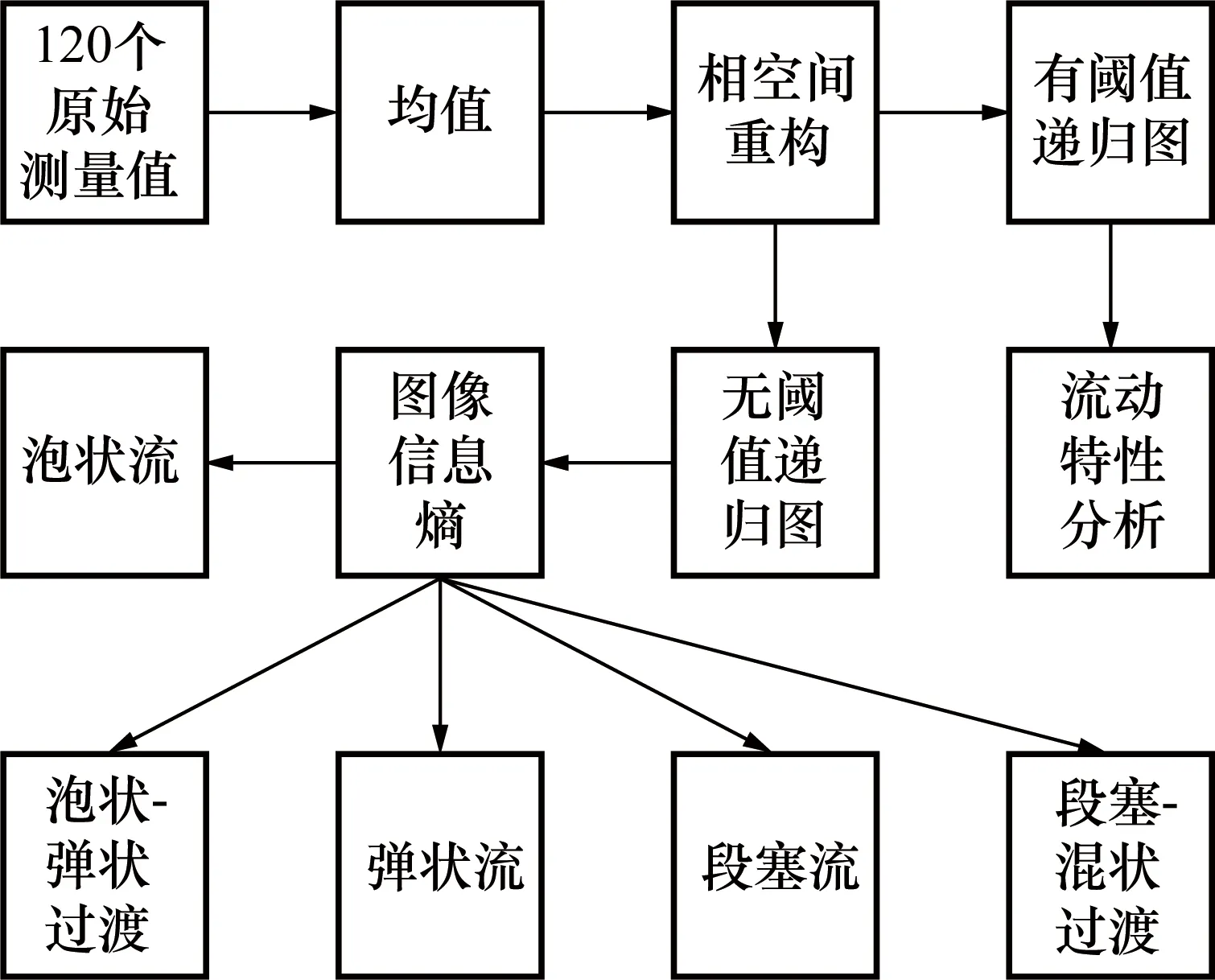
图4 流型辨识步骤Fig.4 Flow pattern identification steps

4.1 递归图分析

对一维均值时间序列进行相空间重构,采用C-C方法计算嵌入维数m与延迟时间τ,3组数据的重构结果如表1所示。

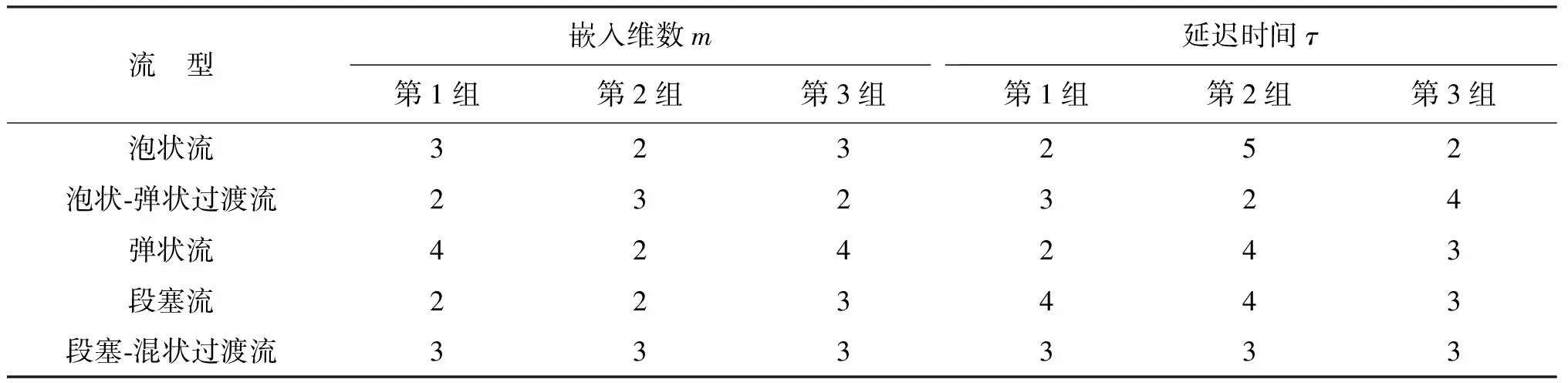
表1不同流型的m、τTab.1 Different flow patterns of m and τ

即使是同种流型,对于不同时段的采集数据,其重构出的相空间维数也会不同,这充分反映了气液两相流流动的复杂性与不确定性。由于嵌入维数与延迟时间的变化对递归结构的性质并无太大影响[18],因此可以固定m、τ绘制每种流型的无阈值递归图,如图5所示。

由图5可见,随着流动变得剧烈,其无阈值递归图图像清晰度变化很大。为进一步分析不同流型流动特性,对递归图进行阈值分割,剔除冗余信息,阈值ε选择为0.9,绘制递归图,如图6所示。

由图6发现:泡状流流动中气泡运动轨迹随机多变,系统具有很强的随机性,其递归图表现为均匀结构,由均匀分布的孤立递归点构成。泡状流到弹状流的过渡过程中,气泡数量增多,部分小气泡开始聚合成大气泡,系统随机性减弱,递归特征开始出现,还伴随着表现并不明显的周期性特点,大气团的出现使得测量值会在某一点产生剧烈变化,递归图中表现为大黑色块状区域。气相流速继续增加,气泡直径变大,大气泡后跟随小气泡,演变成弹状流,系统随机性进一步减弱,周期性增强,此时周期性特点可以被观察到,递归图上黑色块状区域变小变多,同时沿主对角线方向发育的线条纹理增多。段塞流中气塞周期性发生,气塞后跟随分散的小气泡,递归图纹理特征周期性明显,黑色块状区域后跟随沿主对角线方向发展的线条,并以这种结构等间距出现。段塞流到混状流过渡过程中,气塞逐渐被击碎,流动状态变得混乱,递归图中黑色块状区域消失,但是保留了主对角线方向的线条纹理,这是由于此时段塞流的周期性运动特点仍未完全消退导致的。

4.2 流型辨识

阈值的选择直接关系到对递归图保留特征的多少,递归率、确定性、递归熵、平均对角线长度等评价指标都会受到阈值选择的影响,不合适的阈值会对流型识别产生不利影响,因此采用图像清晰度评价指标对无阈值递归图进行分析,结果表明,求取递归图图像信息熵可以有效区别5种流型。

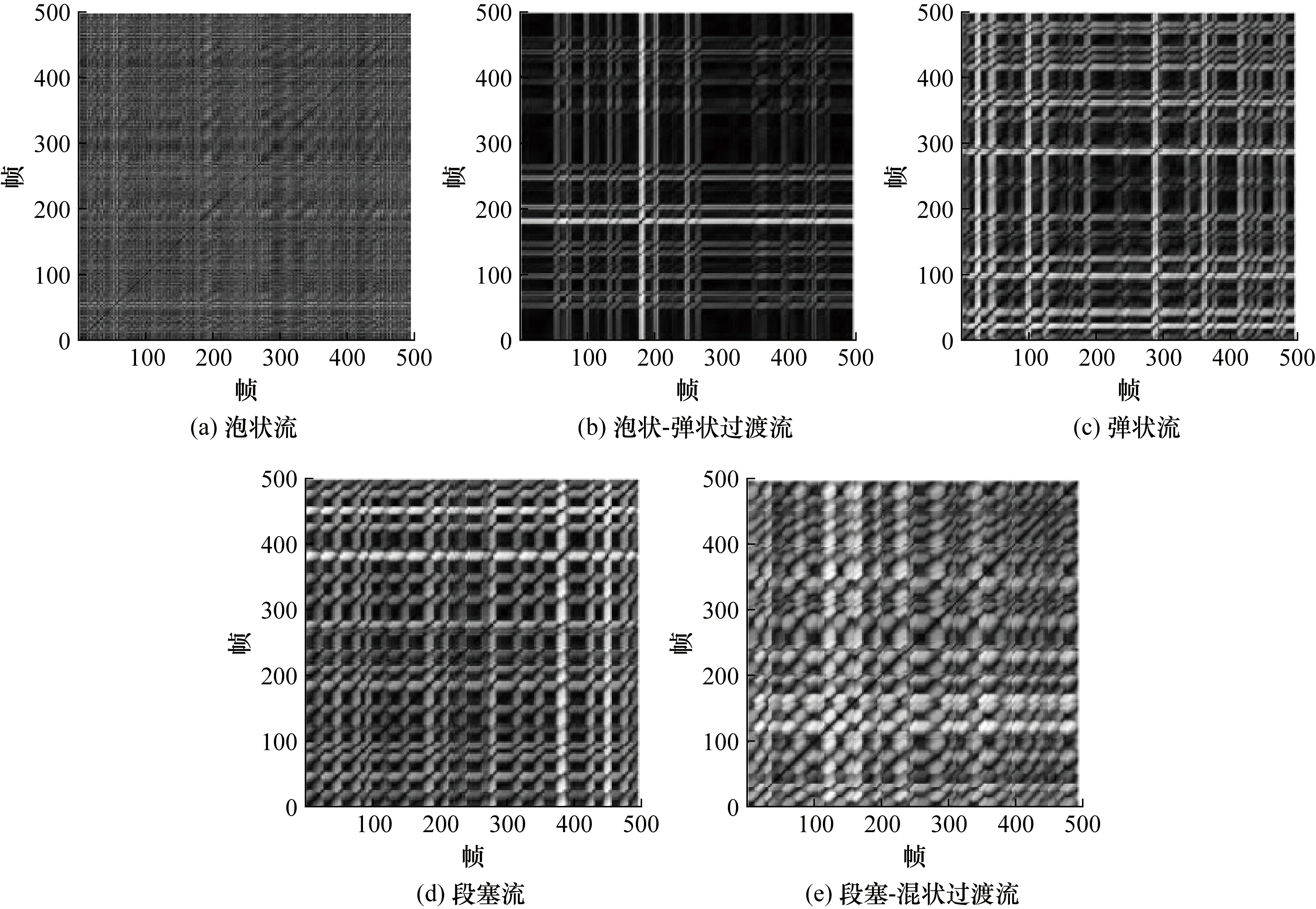
图5 无阈值递归图Fig.5 Threshold free recursive graph

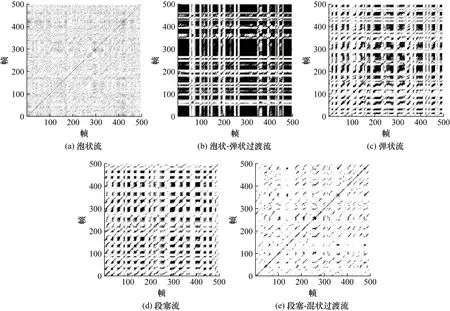
图6 递归图(阈值ε=0.9)Fig.6 Recursive graph(threshold ε=0.9)

当时间序列长度选择为240帧时,每种流型都可以得到780个图像信息熵值。考虑到实际工况下求取嵌入维数与延迟时间比较耗时,因此将嵌入维数固定为3,延迟时间固定为3,对采集到的数据进行递归分析。图7为实验得到5种流型的无阈值递归图图像信息熵值范围,以及落在每个区间内的样本个数。

由图7所示实验结果,得到流型的无阈值递归图图像信息熵范围：泡状流为0.570～0.660;泡状-弹状过渡流为2.300～3.200;弹状流为3.650～4.100;段塞流为4.300～4.600;段塞-混状过渡流为4.650～4.950。因此使用图像信息熵评价指标可以有效区分5种流型,并且发现随着流动状态变得剧烈,流型的无阈值递归图图像信息熵会逐渐增加。

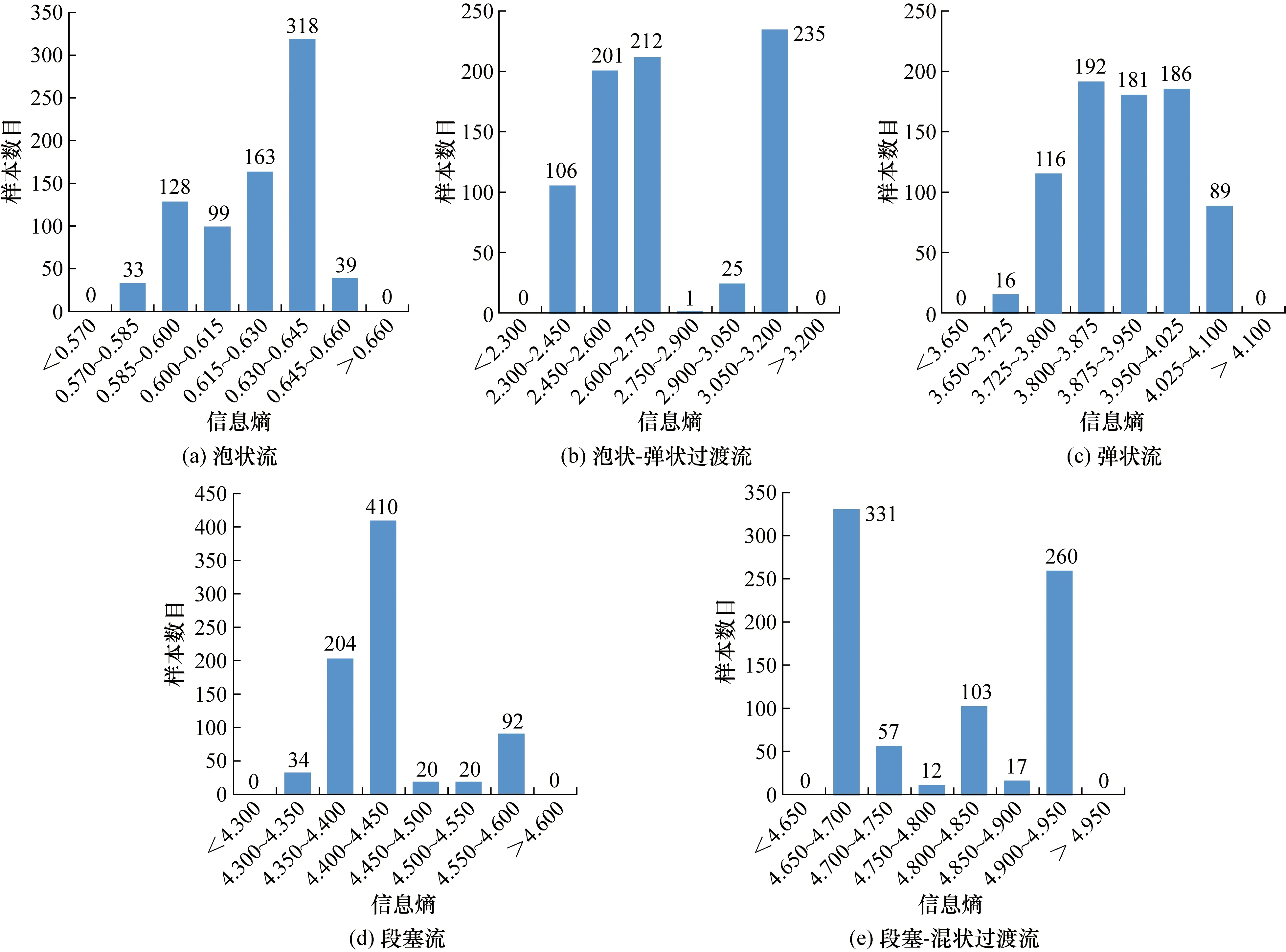
图7 图像信息熵值Fig.7 Image information entropy

5 结 论

对于数字化ERT系统采集的测量数据,通过提取均值进行降维处理,有效减少了计算量,采用C-C算法对一维均值时间序列进行相空间重构,将其映射到高维空间中以分析时序数据的混沌特性,结果表明对于同种流型,其延迟时间与嵌入维数并不固定,这充分反映了气液两相流流动系统的复杂性与不确定性。

根据重构的相空间向量绘制递归图,求取无阈值递归图图像信息熵,进而实现流型辨识,并通过选取合理阈值对递归图进行阈值分割,分析不同流型的流动特点。结果表明,该方法可以有效区分实验生成的泡状流、泡状-弹状过渡流、弹状流、段塞流、段塞-混状过渡流等5种流型,为基于ERT系统的两相流流型辨识提供了新途径。