Monoidal范畴的函子范畴

冯 清 ,黄 菊

（1.福建技术师范学院大数据与人工智能学院,福建福清 350300；2.闽南师范大学数学与统计学院,福建漳州 363000）

1998 年，文献[1]引入了monoidal 范畴，域K上的向量空间，群G的表示均是monoidal 范畴.文献[2-4]中讨论monoidal范畴的一般结构理论、分类问题及不变量.冯清等[5]通过范畴的扩张构造两类monoidal范畴并研究保持问题.通过函子范畴构造monoidal范畴并进一步讨论保持问题.

1 Monoidal范畴的相关概念

Monoidal范畴可视为幺半群的范畴化，先回顾monoidal范畴的相关概念，具体参见文献[1-4].记objD为范畴D的对象集，morD为范畴D的态射集.

定义1Monoidal范畴是指范畴(D,⊗,I,α,l,r)，其中D是范畴，⊗:D×D→D是一个双函子（称⊗为monoidal 积），α:(-⊗-) ⊗-→-⊗(-⊗-)是自然同构，I为范畴D中的对象（称I为单位元），l:I⊗-→idD和r:-⊗I→idD是自然同构且对任意A,B,C,D∈objD有交换图，见图1～2（分别称为五边形公理和三角形公理）.

图1 五边形公理交换图Fig.1 Commutative diagrams of pentagon axiom

图2 三角形公理交换图Fig.2 Commutative diagrams of triangle axiom

特别地，若在monoidal 范畴(D,⊗,I,α,l,r) 中，α=id,l=r=id，即对任意A,B,C∈objD，有(A⊗B) ⊗C→A⊗(B⊗C),I⊗A=A=A⊗I，则称(D,⊗,I,α,l,r)为严格monoidal范畴.

定义2设(D,⊗,I,α,l,r)是monoidal 范畴，若β:-⊗-→-⊗op-是自然同构，且对于任意A,B,C∈objD，有交换图图3.则称(D,⊗,I,α,l,r)为辫子monoidal范畴.

图3 辫子monoidal范畴交换图Fig.3 Commutative diagrams of braided monoidal category

定义3设(D,⊗,I,α,l,r)是monoidal 范畴，若γ:-⊗-→-⊗op-是自然同构，γ2=id，且对任意A,B,C∈objD，有交换图，见图4.则称(D,⊗,I,α,l,r)为对称monoidal范畴.

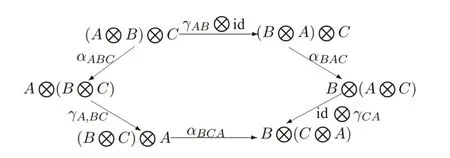
图4 对称monoidal范畴交换图Fig.4 Commutative diagrams of symmetric monoidal category

2 通过函子范畴构造monoidal范畴

函子范畴是两个范畴间的函子所具有的范畴结构，函子范畴的对象是函子，态射为函子间的自然变换.为了引用方便，先来回顾函子范畴的定义，参见文献[6].

定义4设C是小范畴，D是范畴，定义函子范畴DC如下：DC的对象集F:C→D为共变函子.DC的态射集τ:F→G为自然变换.

合成是自然变换的合成.

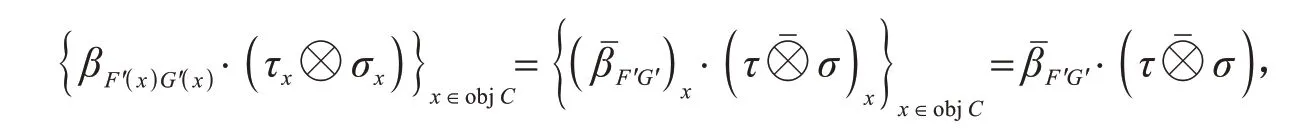
其次，要证(D,⊗,I,α,l,r)是对称monoidal范畴,则也是.只需证.这是因为，同可定义，再由γ2=1可得，从而也是对称monoidal范畴.

例1设k是域，G是有限群，V是k上G-分次向量空间.定义一个新范畴D，其中对象集为objD={Vg|g∈G}，态射集为：若g=h，则morD(Vg,Vh)=k；若g≠h，则morD(Vg,Vh)=0.合成为域中的乘积.定义⊗如下：Vg⊗Vh=Vgh,α⊗β=αβ，其中Vg,Vh∈objD,α,β∈morD.取D中单位元为V1，1 为G的单位元.则对任意Vf,Vg,Vh∈objD有(Vf⊗Vg) ⊗Vh=Vfgh=Vf⊗(Vg⊗Vh),V1⊗Vf=Vf⊗V1=Vf.所以(D,⊗,V1)为严格monoidal范畴.