基于多元线性回归的聚合物透水混凝土性能分析

■张劲桥

（山西路桥第六工程有限公司，晋中 030600）

聚合物透水混凝土作为“海绵城市”建设的重要材料，能够满足城市硬化道路的承重和雨水集疏双重要求，已在各类路面工程中得到广泛应用。 目前，针对聚合物透水混凝土性能的研究较多，吴承彬[1]通过拟合试验数据，给出了不同聚合物透水混凝土性能与胶结材料类型、用量及骨料级配间的量化关系；苏有文等[2]通过试验研究，发现可再分散乳胶粉和羟丙基甲基纤维素可分别提升透水混凝土的强度及透水性指标；施维丽[3]借助多元线性回归模型，建立了聚合物透水混凝土抗压强度与水灰比、聚合物掺量及水泥用量间的函数关系。 本文在前人研究成果的基础上，重点分析了聚合物透水混凝土若干性能间的相互影响关系，借助多元线性回归方法，建立了聚合物透水混凝土性能回归方程，进而深化了对聚合物透水混凝土各项性能形成机理的认识。

1 聚合物透水混凝土概述

聚合物透水混凝土是在普通透水混凝土拌和过程中按要求配合比掺入特定聚合物后，经浇筑、养护形成的具有一定强度和透水功能的实体结构[3]。从宏观层面看，因组分中不含或含极少数细骨料，主要依靠粗骨料与表面附着的水泥及聚合物浆液粘结形成类蜂窝状多孔结构，故同时具备承重和透水两大功能；从微观层面看，聚合物透水混凝土是由固、液、气三相组成的一种非匀质、不等向的多相混合材料，分析其粗骨料的堆积特点发现，聚合物透水混凝土属骨架孔隙结构，如图1 所示；为了达到结构承重及孔隙率指标要求，骨料级配设计采用单级配或开级配方案[3]。 相较于普通透水混凝土，特定聚合物的掺入极大地增强了骨料与混合浆液间的粘结强度，进而在保证透水功能的前提下，大幅提升了透水混凝土的抗压强度和抗变形刚度，透水混凝土路面的路用性能也相应地得到明显改善。 经试验检测，孔隙率为20%的聚合物透水混凝土，其抗压强度指标可达到C30 级普通水泥混凝土水平，而每分钟透水量则高达200 L/m2，透水效率较高[1]，能够满足透水路面的设计及施工要求。

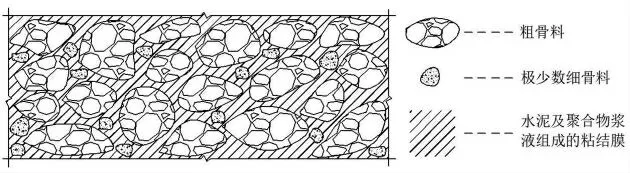
图1 聚合物透水混凝土骨架孔隙结构示意

2 聚合物透水混凝土性能的多元线性回归分析

为进一步探讨聚合物透水混凝土抗压强度、抗折强度、透水系数及孔隙率等性能指标间的相互影响关系，本文引用施维丽[3]的部分试验研究数据，采用多元线性回归方法，拟建立聚合物透水混凝土各性能指标的回归方程， 通过分析回归方程具体参数，进而深入阐释聚合物透水混凝土各性能指标间的内在联系。

2.1 多元线性回归分析的必要性

聚合物透水混凝土具有承重和透水两大典型特性，其中，承重特性主要表现为较高的抗压、抗折强度， 透水特性则体现为较大的透水系数和孔隙率。 为了定量判断聚合物透水混凝土承重与透水特性间的量化关系，从而深化对聚合物透水混凝土典型特性形成机理的认识，故需从各项特性对应的试验数据入手，通过数据拟合建立不同特性指标间的数量关系。 而多元线性回归分析方法适用于包含2个及2 个以上自变量的预测问题，且能够通过多个自变量的最优化组合以协同预测因变量，预测路径更加符合聚合物混凝土性能实际。 综上，有必要采用多元线性回归分析工具定量判断聚合物混凝土各项特性间的相关关系。

2.2 多元线性回归方法简介

多元线性回归是多元回归分析体系中重要的一类分析方法，主要用于研究某一因变量与若干自变量间的线性相关关系，研究结果一般以建立多元线性回归方程的形式表征。 大量线性回归分析实践表明，多元回归模型得出的结果要明显优于一元回归模型；此外，大量非线性回归问题可通过变量代换，转化为线性回归问题，故其具有更广泛的适用性[4]。多元线性回归分析一般包括因变量及自变量确定、回归方程建立、自变量影响程度评价及回归模型检验等步骤[4]。 以下对主要步骤进行简要阐述：

（1）多元线性回归方程建立

考虑到不同自变量的量纲可能存在差异，直接建立回归方程会因变量数量级差异而造成严重的模型失真，故在建立回归方程前需对各自变量进行无量纲化处理，本文采用“min-max 标准化”方法进行处理，计算公式见式（1）[5]：

式中：xi表示经无量纲化处理后的自变量；xi0表示未经无量纲化处理的原始自变量；ximin表示某一自变量中的最小值；ximax表示某一自变量中的最大值。 各自变量经无量纲化处理后，其值全部介于0～1。

假设某一因变量需要i 个自变量进行解释，则其对应的多元线性回归模型的函数表达式见式（2）[4-5]：

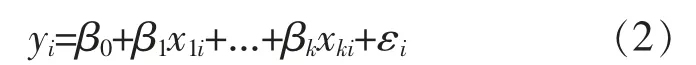
式中：yi表示因变量；β0表示回归常数；βk表示偏回归系数；εi表示随机误差，且服从正态分布。

（2）多元线性回归模型检验

为评价回归方程的拟合程度， 需采用R2法进行检验[4]。 R2计算公式见式（3）：

式中：SST 表示总离差平方和；SSE 表示残差平方和。 具体计算公式见式（4）：

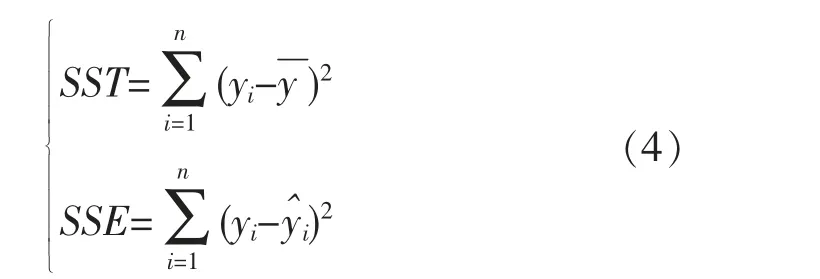
R2值表征了拟合方程对原始数据的拟合程度，其值介于[0，1]范围内，且R2值大小与相应的拟合程度呈正相关关系。

2.3 多元线性回归分析过程及结果

本节引用施维丽[3]的部分试验研究数据作为聚合物透水混凝土性能多元线性回归分析模型的自变量和因变量，详见表1。

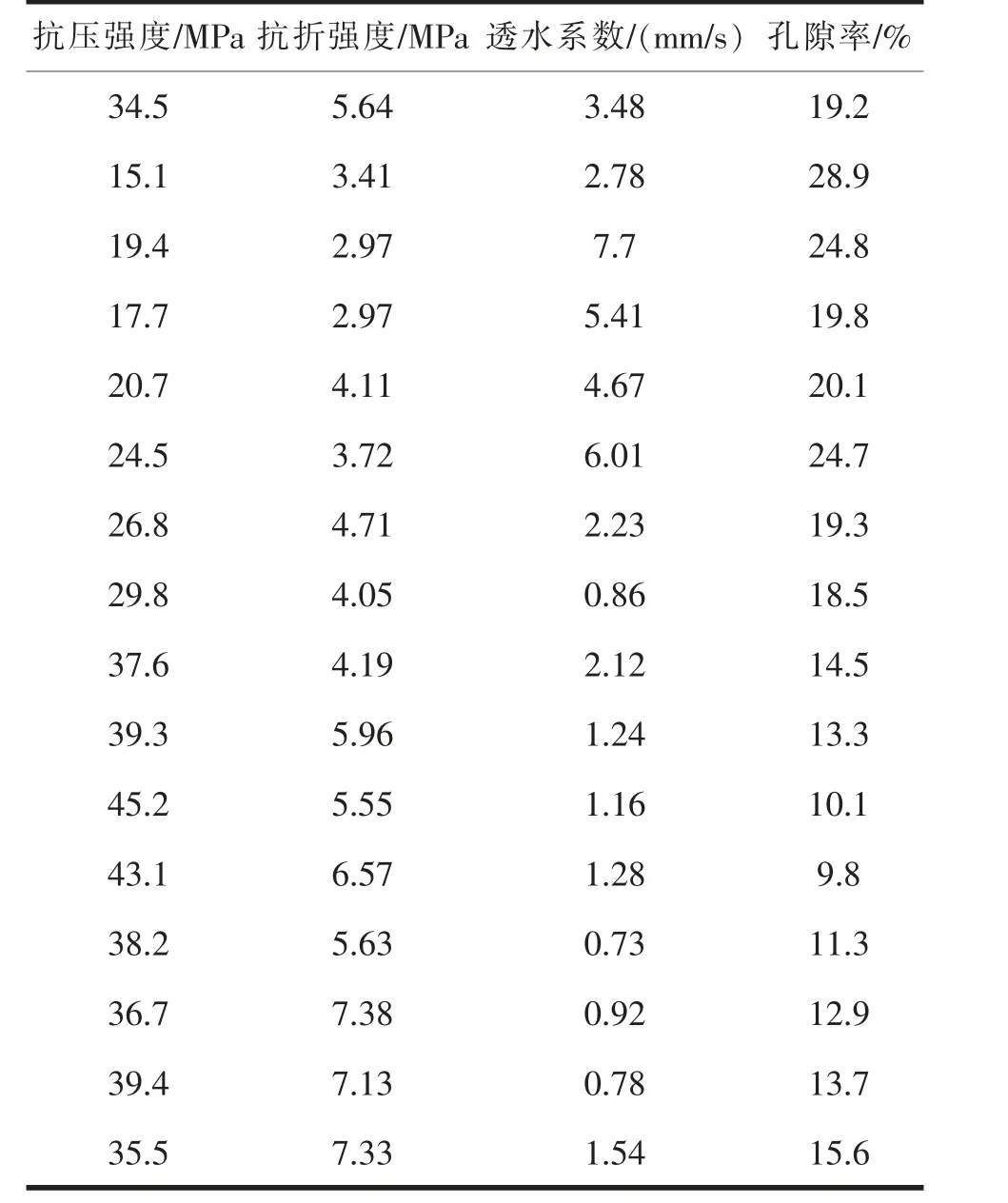
表1 聚合物透水混凝土性能指标试验结果

本节拟先选取抗压强度和抗折强度分别为回归方程的因变量，透水系数及孔隙率为回归方程的自变量，通过多元线性回归分析以对比聚合物透水混凝土透水参数对其不同力学指标的解释程度；回归方程建立及参数计算借助SPSS 统计分析软件中的回归分析模块完成。 具体分析结果见表2。

表2 聚合物透水混凝土性能的多元线性回归分析结果

以y1、y2分别表示因变量抗压强度和抗折强度，x1、x2分别表示自变量孔隙率和透水系数； 因两个回归方程对应的自变量x2的显著性水平均大于0.05，该变量被剔除，最终得出的线性回归方程见式（5）：

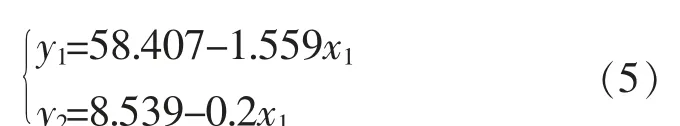
在此基础上，为进一步分析单个力学指标与剩余指标间的函数关系，拟以抗压强度或抗折强度为因变量，剩余三项指标为自变量建立多元线性回归方程，计算过程仍借助SPSS 统计分析软件中的回归分析模块完成。 具体分析结果见表3。

表3 聚合物透水混凝土性能的多元线性回归分析结果

以u1、u2分别表示因变量抗压强度和抗折强度，v1、v2、v3分别表示自变量抗折强度或抗压强度、孔隙率和透水系数； 因两个回归方程u1、u2对应的自变量v1、v3及v2、v3、 的显著性水平均大于0.05，上述变量需剔除，最终得出的线性回归方程见式（6）：

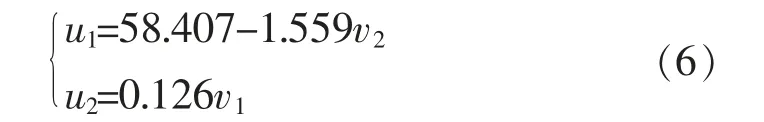
2.4 基于多元线性回归分析结果的性能相关性分析

通过对聚合物透水混凝土性能的多元线性回归分析发现，其力学性能和透水性能间存在线性相关关系，具体表现为聚合物透水混凝土的抗压强度和抗折强度分别与结构的孔隙率呈负线性相关；但抗折强度对应的回归方程的调整后R2值仅为0.509，表明孔隙率与抗折强度间的相关性较低；而抗压强度对应的回归方程的调整后R2值为0.821，表明孔隙率能够充分解释聚合物透水混凝土抗压强度的变化规律，这一结论也侧面印证了聚合物透水混凝土的骨架孔隙结构特性。 此外，聚合物透水混凝土的抗压强度与抗折强度和透水系数无关，而抗折强度一定程度上受抗压强度影响，但对应的回归方程的调整后R2值仅为0.599，相关性程度较低。

3 结论

为进一步研究聚合物透水混凝土力学性能与透水性能间的内在联系， 本文在已有研究基础上，借助多元线性回归模型，建立了聚合物透水混凝土力学性能与透水性能间的回归方程；通过对比回归方程的调整后R2值发现， 聚合物透水混凝土的抗压强度与其孔隙率间存在显著的负线性相关关系，而抗折强度虽也与孔隙率间呈负线性相关，但调整后R2值较小，相关性较低。