二维Volterra-Fredholm积分方程数值算法研究及收敛性分析

解加全 刘霄琪 张佳乐

(1. 太原师范学院数学系，晋中 030619;2. 太原师范学院工程科学计算山西省高等学校重点实验室，晋中 030619)

0 引言

Volterra-Fredholm 积分方程在诸多领域均有广泛应用，如力学、机械、生物、医学以及物理学和应用数学等领域。由于Volterra-Fredholm 积分方程本身结构的复杂性，使得很难通过解析方法获得原问题的解，大多数情形下均采用数值或者半解析方法获取原问题的近似解。目前存在的用于求解Volterra-Fredholm 近似解的方法主要包括谱配点法[1]、伯恩斯坦多项式法[2]、Block-Pulse 函数法[3–4]、泰勒多项式法[5]、斐波那契配点法[6]、Legendre 小波法[7]、Galerkin 方法[8]等。本文主要讨论如下形式的二维Volterra-Fredholm 积分方程，并给出其一般形式

针对Volterra-Fredholm 积分方程(1)的求解，Gouyandeh 等[9]利用Tau 配点法求解了一类非线性Volterra-Fredholm 积分方程的数值解，数值结果表明所提算法具有很高的收敛精度。Ordokhani 和Razzaghi[10]基于Haar 函数和配点法对一类非线性一维Volterra-Fredholm 积分方程进行数值求解，数值结果表明所给算法是有效可行的。Parand 和Rad[11]利用径向基函数方法求解了一类一维Volterra-Fredholm 积分方程的数值解。基于此，本文提出利用二维Block-Pulse 函数方法求解形如方程(1)的二维非线性Volterra-Fredholm 积分方程的数值解，所提算法具有很高的计算效率和满意的数值精度。

1 二维Block-Pulse 函数

1.1 定义

二维Block-Pulse 函数(2D-BPFs)可定义为[12]

其中(x,y)∈[0,T1)×[0,T2)。

3) 完备性

对任意函数f(x,y)∈L2([0,T1)×[0,T2))，当m趋于无穷大时，Parseval 等式

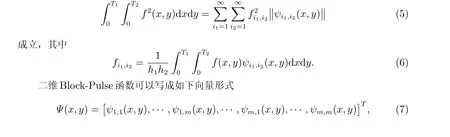
其中X是m2维向量，且˜X=diag(X)。

1.2 函数表示

任意函数f(x,y)∈L2([0,T1)×[0,T2))均可由二维Block-Pulse 函数近似表示为

其中Ψ(x)和Ψ(y)分别是m维Block-Pulse 函数向量。类似地，定义在区间[0,T1)×[0,T2)×[0,T3)×[0,T4)上的四元函数k(x,y,s,t)可由二维Block-Pulse 函数表示为

其中Ψ(x,y)和Ψ(s,t)是m2维二维Block-Pulse 函数向量。

1.3 算子矩阵

向量Ψ(x,y)的积分可表示为

2 求解方法

为了求得方程(1)的近似解，我们首先对函数χ1(x,y,u(x,y))和χ2(x,y,u(x,y))进行近似转化，即

3 收敛性分析

令(C[Γ],//·//)是所有定义在区间Γ= [0,1)×[0,1)上的连续函数所组成的泛函空间，且具有范数

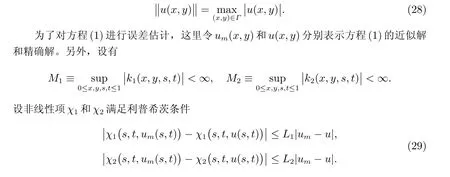
设em(x,y) =um(x,y)−u(x,y)是误差函数，其中um(x,y)是近似解，u(x,y)是精确解，则

只要0<α<1，有//em(x,y)//→0，随着m,n →∞，定理即证。

4 数值算例

例1 考虑如下形式的二维非线性Volterra-Fredholm 积分方程

其中

该问题的解析解是u(x,y)=sin(4πx)sin(4πy)。当m=16,32,64 时，该问题的解析结果和数值结果见图1 至图4。从图1 至图4 可以看出，随着m的增加，数值解越来越逼近于解析解。该问题的解析解是u(x,y)=(x+y)2。当m=8,16,32 时，数值解的二范数误差见表1。

图1 解析解

图2 m=16 时的数值解

图3 m=32 时的数值解

图4 m=64 时的数值解

表1 当m 分别为8、16、32 时，数值解的二范数误差

5 结语

本文以二维Block-Pulse 函数为基函数，对一类二维非线性Volterra-Fredholm 积分方程进行数值求解。通过构造相应的积分算子矩阵和乘积算子矩阵，将原积分问题转化为线性代数方程组，进而离散未知变量获得原问题的数值解。数值结果表明，随着离散项的增加，数值结果越来越逼近于解析结果，且Block-Pulse 函数本身构造简单，在计算过程中会极大提升计算效率。