Dashnic-Zusmanovich型矩阵的子直和

戴平凡, 潘 攀

(三明学院信息工程学院，福建 三明 365004)

0 引言

两个方阵的k-子直和是由Fallat 和Johnson[1]首先介绍，它是通常矩阵和的推广。子直和有许多的应用，例如，矩阵补全问题、域分解方法中的重叠子域、有限元中的整体刚度矩阵等[1–4]。迄今，子直和的性质已被广泛研究[5–10]。给定一类矩阵的k-子直和是否属于相同类？这是一个重要的问题[1–6]。在文献[2]中，Bru 等获得两个非奇异M-矩阵的子直和是非奇异M-矩阵的充分条件。在文献[5]中，Bru 等证明S-严格对角占优矩阵的k-子直和是S-严格对角占优矩阵。此外，∑-严格对角占优矩阵、双对角占优矩阵、α1-矩阵、α2-矩阵、H-矩阵、B-矩阵和双B-矩阵的子直和问题在文献[6—10]中分别被研究。最近，Li 等分别研究了Nekrasov 矩阵[11]和弱链对角占优矩阵[12]的子直和问题。Gao 等研究了QN-矩阵的子直和[13]。

在文献[14]中，Zhao 等定义了Dashnic-Zusmanovich 型(DZ-型)矩阵且给了一个新的矩阵特征值定位集。本文关注DZ-型矩阵的子直和，将提供一些充分条件，使得DZ-型矩阵的k-子直和仍是DZ-型矩阵。

本文中，记号C 指复数域，Cn×n指n阶复矩阵，|a|指复数a的模。

定义1[1]设A ∈Cn1×n1, B ∈Cn2×n2且A22,B11∈Ck×k(1≤k ≤min(n1,n2))，

其中t=n1−k, S1={1,··· ,n1−k}, S2={n1−k+1,··· ,n1}, S3={n1+1,...,n}。如果我们记

其中

文献[14]指出DZ-型矩阵类是H-矩阵的一个子类，且包含严格对角占优矩阵类。

1 主要结果

首先，给一个例子指出，两个DZ-型矩阵的子直和可能不是一个DZ-型矩阵。考虑DZ-型矩阵A和B如下

它们的1-子直和C=A ⊕1B为

这里C不是DZ-型矩阵，因为对i=4，不存在指标j ∈{1,2,3,5}，使得(2)式成立。

上面例子促使我们寻找DZ-型矩阵的子直和仍是DZ-型矩阵的条件，我们首先研究DZ-型矩阵的1-子直和。

定理1 假定A=(aij)和B=(bij)分别是形如(1)中n1和n2阶的分块矩阵。设k=1 和S1={1,··· ,n1−1}, S2={n1}, S3={n1+1,··· ,n}，其中n=n1+n2−k。设A和B是DZ-型矩阵，如果A22和B11的所有对角元素对应成任意正比例，并且下列条件

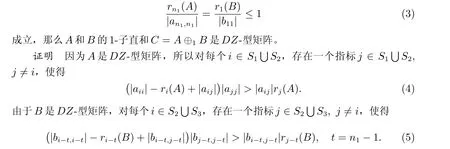
对每个i ∈S3，如果(5)式中j/∈S2，即(5)式中j ∈S3{i}，那么我们有

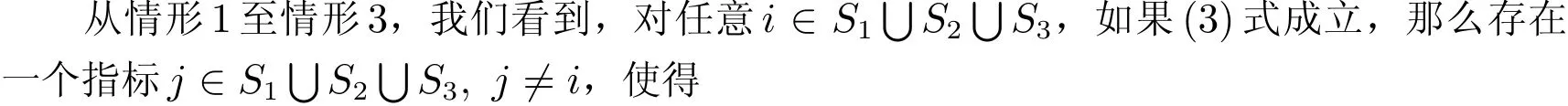
故1-子直和C=A ⊕1B是DZ-型矩阵。

定理2 假定A=(aij)和B=(bij)分别是形如(1)中n1和n2阶的分块矩阵。设k=1 和S1={1,··· ,n1−1}, S2={n1}, S3={n1+1,··· ,n}，其中n=n1+n2−k。设A和B是DZ-型矩阵，如果A22和B11的所有对角元素对应成任意正比例，并且下列条件之一成立：

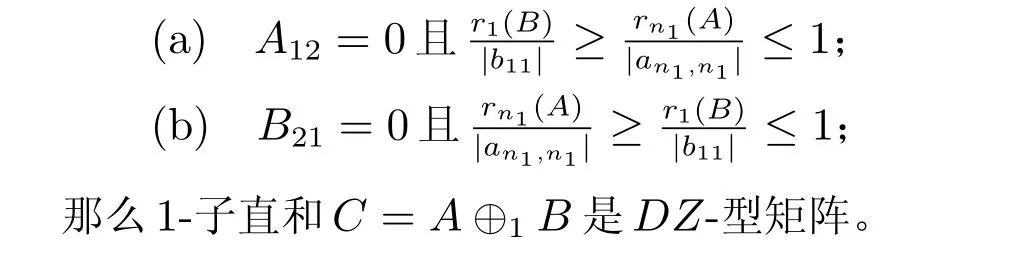
因此，C=A ⊕1B是DZ-型矩阵的条件刚好包含在(a)中。

(b)的证明类似于(a)的情况。因此，结论成立。

类似于定理2 的证明，不难获得下列推论。

推论1 假定A=(aij)和B=(bij)分别是形如(1)中n1和n2阶的分块矩阵。设k=1 和S1={1,··· ,n1−1}, S2={n1}, S3={n1+1,··· ,n}，其中n=n1+n2−k。设A和B是DZ-型矩阵，如果A22和B11的所有对角元素对应成任意正比例，A12=B21=0，且下列条件成立：

因为对每个i ∈{1,2,··· ,7}，至少存在一个指标j ∈{1,2,··· ,7}{i}，使得

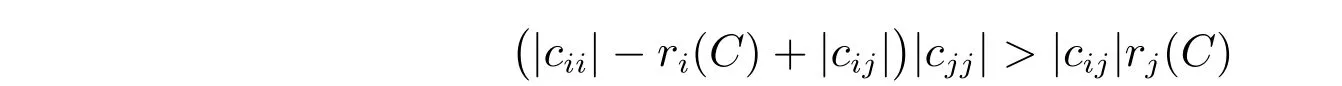
成立，所以1-子直和C=A ⊕1B是DZ-型矩阵。

下面的例子表明两个DZ-型矩阵的1-子直和是一个DZ-型矩阵，但DZ-型矩阵的2-子直和C=A ⊕2B不是DZ-型矩阵。

例2 考虑下列DZ-型矩阵

这里C不是DZ-型矩阵，因为对i=6，没有指标j ∈{1,2,3,4,5}，使得

成立。

例2 促使我们研究C=A ⊕k B对k ≥2 是否是DZ-型矩阵的问题，当A和B是DZ-型矩阵，我们需要下列辅助结论。

引理2 假设A= (aij)和B= (bij)分别是形如(1)中n1和n2阶的分块矩阵。设S1={1,··· ,n1−k}, S2={n1−k+1,··· ,n1}, S3={n1+1,··· ,n}，其中2≤k ≤min{n1,n2}, n=n1+n2−k。设A和B是DZ-型矩阵，如果A22和B11的所有对角元素对应成任意正比例且

成立。

情形2 对每个i ∈S2，注意到存在j ∈S1，使得(10)式成立，那么用条件(9)和引理1，我们能推断

对每个i ∈S3，如果(11)式中j/∈S2，即(11)式中j ∈S3{i}，那么我们有

成立，故当2≤k ≤min(n1,n2)时，k-子直和C=A ⊕1B是DZ-型矩阵。

注1 当2≤k ≤min(n1,n2)时，k-子直和C=A ⊕k B是DZ-型矩阵所要求的条件与当k=1 时，1-子直和C=A ⊕1B是DZ-型矩阵的条件相同。

这里C是DZ-型矩阵，因为对任意指标i ∈ {1,2,··· ,6}，至少存在一个指标j ∈{1,2,··· ,6}{i}，使得

成立。

在一些应用中，例如，域分解[15–16]、矩阵A和B是形如(1)中的分块矩阵，且带有一个相同的块，即A22=B11。像定理3 一样，我们可以给一些充分条件：当A22=B11时确保k-子直和C=A ⊕k B是一个DZ-型矩阵，在此之前我们需要下列结果。

引理3 假设A= (aij)和B= (bij)分别是形如(1)分块的n1和n2阶矩阵，且S1={1,··· ,n1−k}, S2={n1−k+ 1,··· ,n1}, S3={n1+ 1,··· ,n}，其中2≤k ≤min(n1,n2), n=n1+n2−k。设A和B是DZ-型矩阵，如果A22=B11，下列不等式

因此，由(12)式、引理2 证明中不等式推导之最后三个等式，可由下列两个等式替换

故结果成立。

因此，我们得到结论：k-子直和C=A ⊕k B,2≤k ≤min(n1,n2)，是DZ-型矩阵。类似上面的证明，由条件(b)易得k-子直和C=A ⊕k B是DZ-型矩阵。

推论2 假设A= (aij)和B= (bij)分别是形如(1)分块的n1阶和n2阶DZ-型矩阵，且S1={1,··· ,n1−k}, S2={n1−k+ 1,··· ,n1}, S3={n1+ 1,··· ,n}，其中2≤k ≤min(n1,n2), n=n1+n2−k。设A和B是DZ-型矩阵，如果A22=B11, A12=B21=0，则

这里C是DZ-型矩阵，对任意i ∈{1,2,··· ,6}，存在j ∈{1,2,··· ,6}{i}，使得

这里C是DZ-型矩阵，对任意i ∈{1,2,··· ,6}，存在j ∈{1,2,··· ,6}{i}，使得

成立。

2 结论

本文给出了判定Dashnic-Zusmanovich 型矩阵的子直和是Dashnic-Zusmanovich 型矩阵的一些充分条件。特别地，我们找到了一些容易检测的条件，使得当A和B是DZ-型矩阵时，1-子直和C=A ⊕1B是DZ-型矩阵。例2 表明：当k ≥2 时，C=A ⊕k B可能不是DZ-型矩阵。像1-子直和C=A ⊕1B一样，我们也找到了一些充分条件：当k ≥2 且A和B是DZ-型矩阵时，DZ-型矩阵的子直和C=A⊕k B仍是DZ-型矩阵。