惯性张量平移和旋转复合变换的一般形式及其应用
2022-12-19陈强洪甄文强
黎 旭, 陈强洪, 甄文强, 王 硕
(中国工程物理研究院总体工程研究所,绵阳 621999)
0 引言
在汽车等领域的工程设计中,由于各组件惯性矩和惯性积参考系、安装位置和姿态各不相同,常常需要将复杂系统不同组件的惯性矩(转动惯量)、惯性积进行变换后合成[1–3]。特别是像运载火箭的质量特性随时间变化的情况下,实现飞行轨迹计算时需要对惯性张量进行合成,现有方法主要是通过实物测量和CAD 模型测量获得合成的惯性矩和惯性积。实物测量对测量设备要求较高,周期和成本也较高;CAD 模型测量需要建立完整的三维模型并赋相应的密度,只能对静态模型进行合成,无法对惯性矩和惯性积进行快速合成。
为实现随时间变化的不同刚体组件惯性矩和惯性积的快速合成,需要对其进行坐标变换,已有文献给出了刚体惯性矩和惯性积分别进行平移或旋转变换的形式[4–7],但缺少平移、旋转复合变换的一般形式。本文首先从惯性张量的基本定义出发,采用矩阵变换导出了一般的惯性张量分量矩阵平移和旋转变换关系,然后将不同坐标系下的组件惯性张量变换到同一坐标系下,最后直接叠加实现惯性矩和惯性积的快速合成,方法具有一定理论意义和工程使用价值。
1 惯性矩、惯性积与惯性张量的描述
惯性张量是描述刚体做定点转动的物理量,包含惯性矩和惯性积信息[8]。为了描述惯性张量,定义直角坐标系O −xyz(S),x、y、z方向的基元分别为i、j、k,则刚体上任意一点的位置矢量可表示为

其中u为刚体上任意一点的位置矢量,f为坐标系S的基元构成的矢阵(f=[i,j,k]T),r为u在S中的坐标(r=[x,y,z]T)。
刚体的惯性张量定义为[3]

其中I为刚体惯性张量,u为刚体上任意一点的位置矢量,u · u为内积,uu为并矢,E为单位张量。
由式(1)和式(2),可得

其中J为惯性张量I在S中的分量矩阵(惯性矩阵)[3,7–8],形式为

其中Jxx为相对x轴的惯性矩,Jyy为刚体相对y轴的惯性矩,Jzz为刚体相对z轴的惯性矩,Jxy为刚体相对x、y轴的惯性积,Jyz为刚体相对y、z轴的惯性积,Jzx为刚体相对z、x轴的惯性积,其中Jzx=Jxz。
2 惯性张量平移和旋转变换的一般关系
2.1 位置矢量的坐标变换关系
为了将局部坐标系下的惯性张量分量矩阵变换到全局坐标系下,首先需要知道局部坐标系与全局坐标系的坐标变换关系。构造如图1 所示的两个坐标系,O1x1y1z1(S1)为局部坐标系,O2x2y2z2(S2)为全局坐标系。O1相对于O2的位置矢量为u0,在S2中的坐标为r0。刚体上任一点A相对于O1的位置矢量为u1,在S1中的坐标为r1。A相对于O2的位置矢量为u2,在S2中的坐标为r2,刚体在S1下的质心坐标为rC。
由图1 中的几何关系可得

图1 刚体的坐标变换关系

写成坐标系下的形式为

由S2的基元矢阵f2通过基元旋转,可得到S1的基元矢阵

其中L为旋转矩阵,同时也是正交矩阵。任何两个坐标轴不平行的坐标系可以通过若干次基元旋转变成各轴互相平行的坐标系,这里按照z −y −x的顺序(也可以其它顺序)旋转f2至与f1平行,通过三次如图2 所示的Euler 角基元旋转实现。

图2 坐标系的基元变换
旋转变换矩阵为

式(7)带入式(6),可得包含平移和旋转的坐标变换关系

2.2 惯性张量分量矩阵的变换关系
得到刚体位置矢量的坐标变换关系后,下面考虑坐标变换下的张量矩阵关系。由式(4)可知,全局坐标系S2下的惯性张量分量矩阵为

将式(12)∼(15)带入式(11),得变换关系

分几种情况讨论:
1) 当r0= 0 时,即局部坐标系原点O1与全局坐标系原点O2重合,此时为纯旋转变换,式(16)简化为

2) 当r0̸= 0 且L=E时,此时为纯平移变换,变换关系为惯量平移定理,式(16)简化为

3) 当rC=0 时,即局部坐标系原点O1与刚体质心重合,平移变换和旋转变换的作用相互独立,式(16)简化为

4) 当r0̸= 0 且rC̸= 0 时,即局部坐标系原点O1与全局坐标系原点O2不重合,且局部坐标系原点O1与刚体质心不重合,则式(16)中存在交叉项,表明平移和旋转变换存在耦合效应。
3 算例分析
考虑某飞行器舱段内三个组件的惯性矩、惯性积合成问题,已知组件在本体局部坐标系下的质量特性如表1 所示。
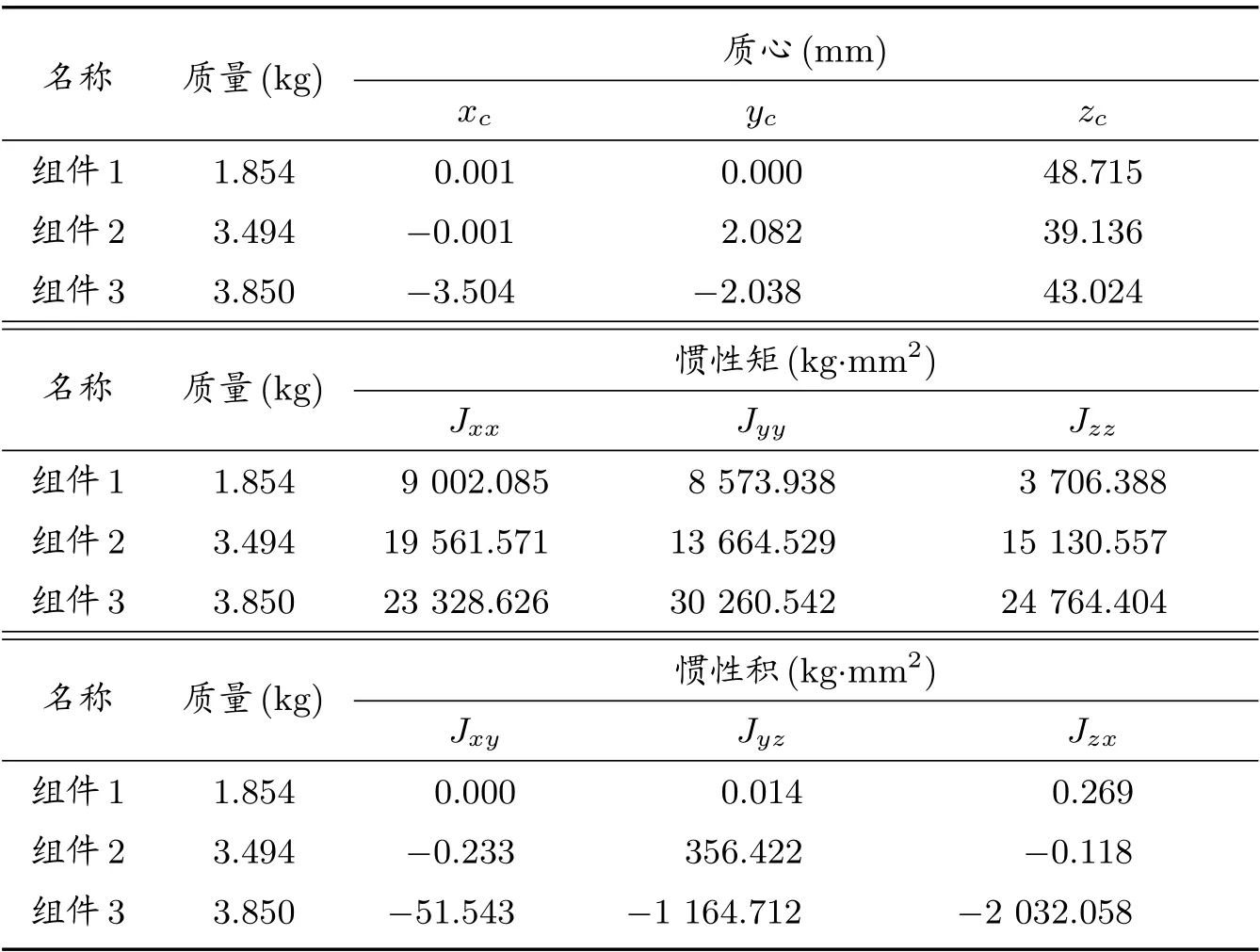
表1 组件本体局部坐标系下质量特性
假设三个组件未安装时的本体局部坐标系与舱段全局坐标系重合,安装好后本体局部坐标系相对全局坐标系先进行旋转变换,然后进行平移变换,变换参数如表2 所示。

表2 组件平移和旋转变换参数
组件安装好后,相对于舱段全局坐标系的惯性矩和惯性积如表3 所示,其中计算值为本文计算结果,CAD 为三维软件(NX UG 12.0)的测量结果。可以看出,计算结果与CAD 测量结果几乎一致,微小的差异主要为数值舍入误差导致,可忽略不计。结果表明,本文所推导的惯性张量复合变换的公式正确,可以作为工程中惯性矩和惯性积快速合成提供依据。
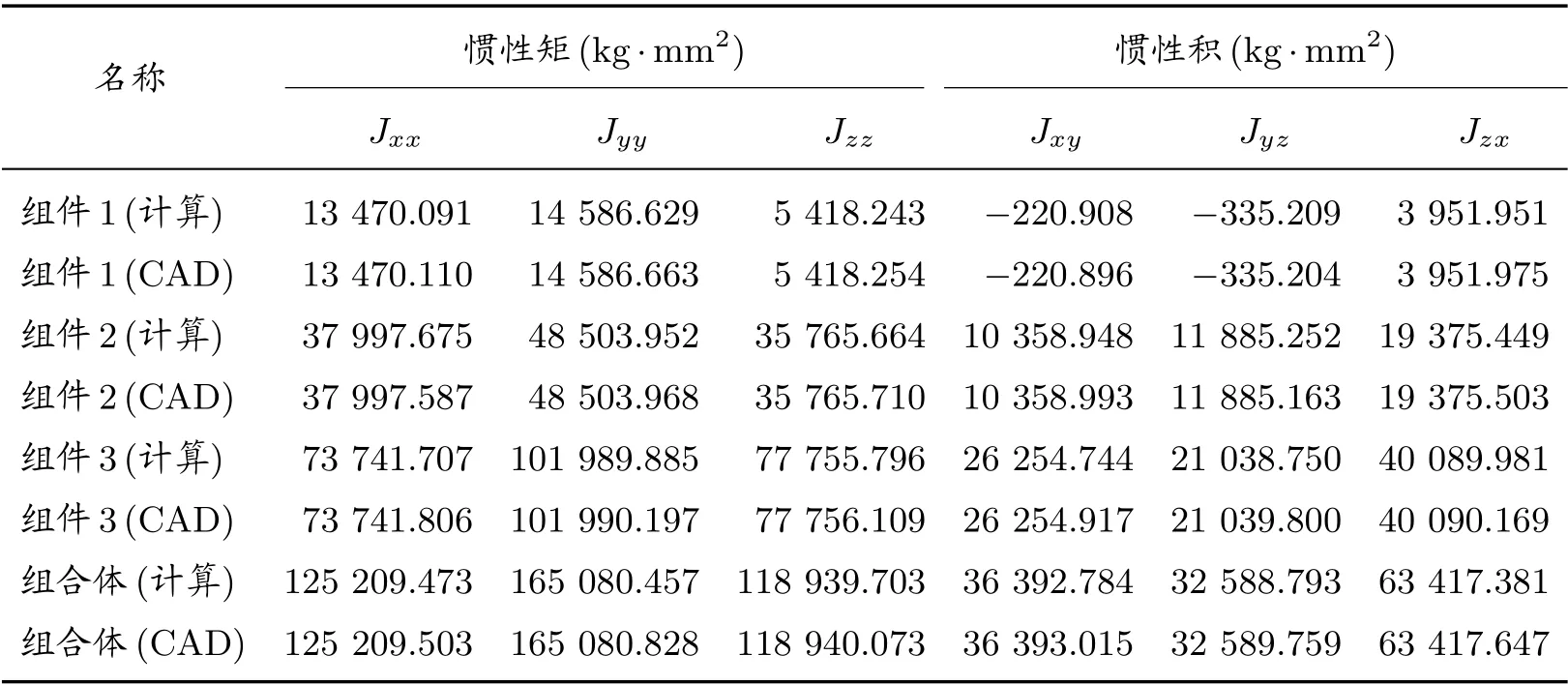
表3 组件全局坐标系下惯性矩、惯性积
4 总结
本文首先基于惯性张量的基本定义,采用矩阵变换推导出了惯性张量分量矩阵平移和旋转复合变换的一般形式,然后给出了不同简化条件下的结论。最后,通过某飞行器三组件惯性矩、惯性积合成的算例验证了结论的正确性。
这种方法通过简单的组合计算,就能够在了解各组件随时间变化的数据基础上,适应组合系统的惯性张量计算需求。
