非线性扰动的切换系统的异步控制：模态依赖的平均驻留时间方法

高 娟, 李同彬

(1. 哈尔滨师范大学数学科学学院，哈尔滨 150001; 2. 哈尔滨师范大学经济学院，哈尔滨 150001)

0 引言

切换系统属于一类重要的混合系统，由有限数量的子系统和协调子系统之间切换的切换信号表示，研究此类系统的动机主要有两方面。首先，许多真实系统可以建模为切换系统；其次，多控制器切换提供了一种有效的机制来处理高度复杂的系统。由于多个子系统和各种可能的切换信号，切换系统表现出非常复杂的动力学行为。切换系统的研究越来越受到人们的重视，特别是切换系统的稳定性分析和控制设计是研究的重点。

稳定性问题是切换系统的基本研究问题之一，已有的研究结果可分为两类：任意切换下的稳定性和约束切换下的稳定性[1–7]。对于切换系统，只要构造一个公共李雅普诺夫函数，就可以保证系统在任意切换下的稳定性。然而，大多数切换系统不具有共同的李雅普诺夫函数，并且在任意切换下无法保持稳定性，但通过使用多李雅普诺夫函数技术和设计适当的切换律仍然可以保证稳定性。设计适当切换律的有效方法是平均驻留时间(ADT)方法[3,8]。ADT 已被许多研究人员广泛用于研究切换系统的稳定性问题[9–10]。最近，作者在文献[11]中提出了模态依赖平均驻留时间(MDADT)方法，其中每个子系统都有自己的ADT。MDADT 已被证明是一类更具一般性的ADT[12–14]。

控制问题是为系统设计一组控制器，使系统在一定的切换信号下稳定并获得更好的性能，学者们已经对其进行了广泛的研究[15–18]。然而，在控制器设计中，通常假设控制器和子系统同步切换，这是不现实的。正如文献[19—20]中所述，在实际操作中，需要一些时间来识别运行的子系统和应用与之匹配的控制器，所以子系统和控制器之间不可避免地存在异步切换。因此，有必要为切换系统设计异步切换控制器。近年来，关于异步切换控制的研究大量涌现，如状态反馈镇定[15,21–23]、输出反馈镇定[24–25]和H∞滤波[26–28]等。

基于上述讨论，本文使用模态依赖平均驻留时间技术研究了切换系统的异步控制。另外，考虑到切换系统在实际应用中不可避免地受到外部因素的干扰。因此，非线性扰动的切换系统的异步控制问题具有重要研究价值。

与文献[22—23]相比，本文的创新点如下：

1) 使用模态依赖的平均驻留时间方法设计比平均驻留时间方法保守性低的切换律；

2) 利用异步切换系统状态方程的解析解直接研究系统的动力学，而无需构造任何李雅普诺夫函数，从不同的角度去理解这个问题。

1 问题描述及引理

考虑如下带有非线性扰动的切换系统

其中γ>0 为常数。

注1 条件(2)称为李普希茨约束(L 约束)，这说明该模型对输入干扰不敏感，并且可以提高模型的泛化性能。

令σ′(t)表示控制器的实际切换信号，控制器的实际切换序列为

其中

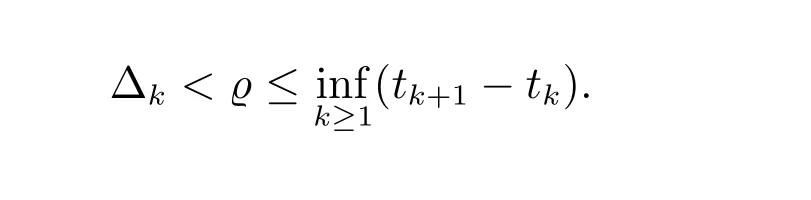
∆k>0(或∆k<0)表示控制器的切换时刻滞后(或超前)于子系统的切换时刻，不失一般性，本文考虑∆k>0。

考虑状态反馈控制器

2 主要结果

2.1 稳定性分析

本节研究闭环切换系统(4)的稳定性。为方便描述，令T−p(0,t)(T+p(0,t))表示第p个子系统在时间区间[0,t)上受控于匹配(不匹配)的控制器的总时间。Re(¯Apq)表示矩阵¯Apq的特征值的实部。

证明 依据βp的值，将所有的子系统分为两类：如果βp ≤−αp，子系统属于集合S1={1,2,··· ,l}，否则，属于集合S2={l+1,··· ,N}。

由式(8)，可得

重复上面的过程，对于任意的t ∈[¯tk,tk+1)，我们也可以得到不等式(15)。于是，对于任意的t ∈[tk,tk+1)，不等式(15)成立。

由定义2，可知闭环系统(4)在切换信号(9)下是全局一致指数稳定的。

2.2 控制器设计

本节给出状态反馈控制器的设计方法。

将式(23)分别代入到等式¯Ap=Ap+BpKp和¯Apq=Ap+BpKq中，可以得到矩阵¯Ap和¯Apq。进一步，由式(12)可得矩阵Fp和Fpq。常数ξp和˜ξp可以由关系式得到。因此，根据定理1，切换系统(1)在切换信号(9)下是异步稳定的。

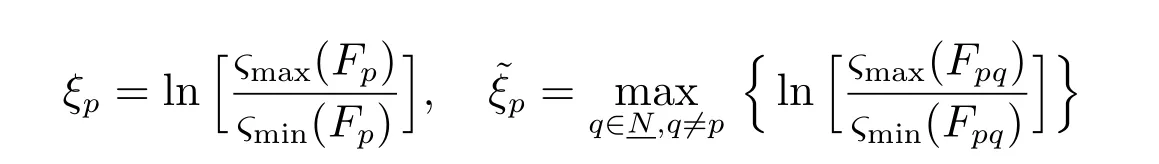
注2 定理2 中对切换时滞和的比率没有约束。而在文献[24]的定理1 中，切换时滞之和的比率需要小于某个值。从这一点来看，本文的结果更加灵活。

基于定理1 和定理2，下面给出算法1，计算状态反馈控制器增益和最小MDADT 的算法，具体的求解步骤如下：

3 数值仿真

下面给出一个数值例子来验证本文方法的有效性。

考虑由三个子系统组成的切换系统(1)，子系统矩阵参数为

其中A1、A2和A3是不稳定的。取γ=0.1，我们的目标是设计状态反馈控制器和MDADT切换信号，使得系统在异步切换下稳定。异步切换所涉及的时滞为∆1M= 0.5,∆2M=0.4,∆3M=0.7。

为了显示MDADT 相较ADT 的优势，设计使得系统稳定的ADT，我们知道ADT 不要求参数α、β、ξ、˜ξ和∆M依赖模态，即α1=α2=α3, β1=β2=β3, ξ1=ξ2=ξ3,˜ξ1= ˜ξ2= ˜ξ3,∆1M=∆2M=∆3M。不妨取

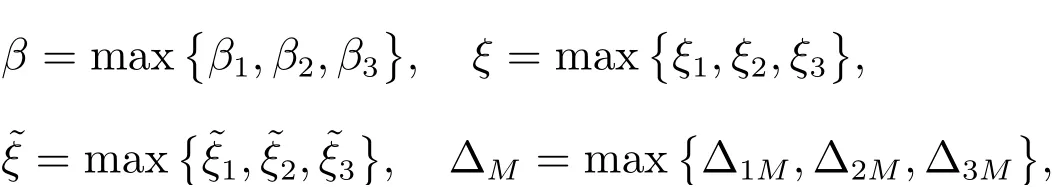
平均驻留时间为

通过设定适当的参数，然后根据算法1 计算MDADT 和ADT，计算结果见表1。给定参数α1= 0.8, α2= 0.6 和α3= 0.7，最小的MDADT 是τ∗1= 7.358 0,τ∗2=15.709 4 和τ∗3=9.391 3。给定参数α=0.6，最小的ADT 是τ∗=15.851 0，可见ADT 大于MDADT。因此，MDADT 切换信号比ADT 切换信号更具灵活性。

表1 两种不同切换信号的参数设定和计算结果

根据算法1，可得控制器增益为

接下来，进行仿真。取τ1= 7.4, τ2= 15.8 和τ3= 9.4。图1 描述了切换信号，图2 给出了闭环系统在初值x0= [−0.2 0.3]T下的状态曲线。可以看到，切换系统在设计的切换信号和控制器下是稳定的。

图1 切换信号

图2 闭环系统的状态响应

4 结论

本文研究了具有非线性扰动的切换系统的异步控制问题，通过分析系统状态方程的解析解并利用MDADT 方法，推导了系统指数稳定的条件。然后，形成了相应的控制器可解条件。此外，给出了控制器设计和最小MDADT 的算法，该方法可用于处理非线性扰动切换系统的异步有限时间控制问题，这将是未来工作中一个有趣的课题。