多根非线性方程组求解的探路者灰狼算法

逯 苗, 曲良东, 何登旭

(广西民族大学数学与物理学院，南宁 530006)

0 引言

非线性方程组是数学学科中的一个重要组成部分[1–2]，在现实生活中，很多物理[3]、工程[4]类问题最后都可归结为非线性方程组的求解问题。因此，对求解非线性方程组，尤其是多根非线性方程组的研究具有重要研究意义。目前有很多应用传统的方法对多根非线性方程组求解，比如：牛顿法[5]、迭代法[6]等。但传统算法对迭代初始值的选取比较严格，或需要计算导数和矩阵求逆，对于有些复杂的方程组不存在导数或很难求解时，这些算法就产生一定的局限性，即使找到方程组的近似解，但是精度较差[7]。

随着群智能算法应用领域的不断被扩充，群智能算法被广泛应用到求解多根非线性方程组，在求解问题时，首先将多根非线性方程组问题转化为优化问题，即转化成单目标优化问题或多目标优化问题两种方法。近年来，Pourrajabian 等[8]将遗传算法和增广拉格朗日函数进行结合求解简单非线性方程组。Ali 等[9]利用差分进化算法结合精英反向学习以及变步长随机定位的概念等，提出了求解多目标优化问题的改进差分进化算法。王冬冬和周永权[10]将人工鱼群算法应用于非线性方程组的求解问题。欧阳艾嘉等[11]将Hooke-Jeeves 算法与粒子群算法结合提出求解非线性方程组的混合粒子群优化算法。赵光伟和周永权[12]提出人工萤火虫算法和复合形法相结合的方法求解非线性方程组的问题。Abdollahi 等[13]采用帝国主义竞争算法求解非线性方程组等。

群智能算法具有结构简单，收敛速度快。因此，将群智能优化算法应用于非线性方程组求解时对初始解要求不高，不需要进行求导，而且具有较强的鲁棒性。但在多根非线性方程组的求解过程中仍然存在求解个数不完全、精度不高等问题。为解决这一问题，本文提出探路者灰狼优化算法，受探路者算法中跟随者的启发，对灰狼种群中β、δ、ω个体位置的更新原则进行改变；重新设计位置更新公式等对原灰狼算法进行改造，进而对多根非线性方程组进行求解，通过仿真实验以及和其他智能算法的比较，进一步验证该算法在多根非线性方程组的求解问题上有良好的求解效果。

1 非线性方程组

设一个非线性方程组由n个方程组成，涉及n个未知量，形式如下

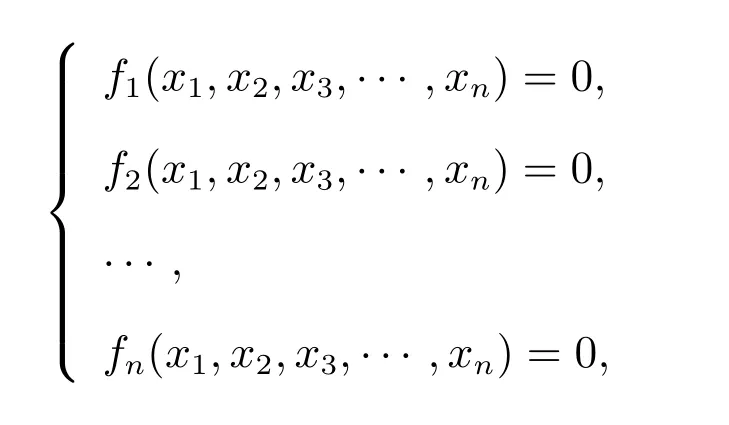
其中fi(X) =Ai(i= 1,2,··· ,n)为非线性方程组，X= [x1,x2,··· ,xn]为方程组的未知向量，Ai(i= 1,2,··· ,n)为常数项。群智能优化算法在求解非线性方程组的问题时，需要将非线性方程组问题转换为优化问题。将非线性方程组转化为单目标优化问题，其表达形式为

那么求非线性方程组的解的问题就转化成了求适应度函数F(X)最小值的问题。本文选取公式(1)的方法求解非线性方程组的解。

2 灰狼优化算法和探路者算法

2.1 灰狼优化算法

灰狼优化算法(Grey Wolf Optimiztion, GWO)[14]是一种新型群智能优化算法，主要模拟灰狼的社会等级和捕食行为。种群中的头狼称为α，其次为β，然后是δ，其余狼称为ω。在求解函数优化问题时，假设灰狼种群规模为N，搜索维度为d维，xi=(xi1,xi2,··· ,xid)用来表示第i只灰狼在d维空间的位置，它们对猎物的搜索行为可以通过以下数学模型进行描述

其中Xp(t)表示第t代猎物的位置；X(t)表示第t代灰狼个体的位置；常数C为摆动因子，由式(5)决定，A为收敛因子，由式(6)决定

其中r1和r2是取值在[0,1]之间的随机向量，a在迭代中从2 线性地减小到0。

对于每一只ω狼，首先根据

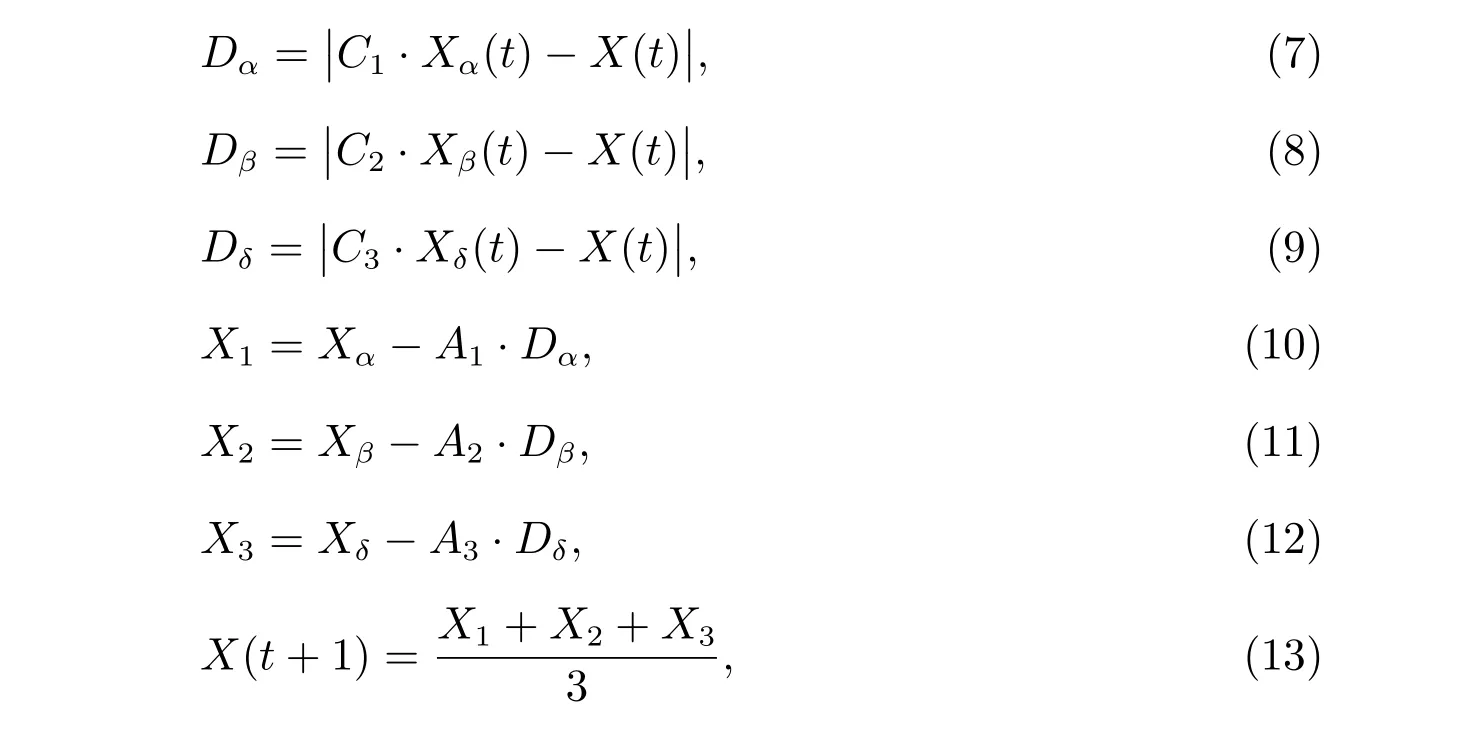
计算它们与α、β、δ的距离，然后由式(13)综合判断出灰狼个体向猎物移动的方向。Xα表示α狼的位置，Xβ表示β狼的位置，Xδ表示δ狼的位置，C1、C2、C3是随机向量。

2.2 探路者算法

探路者算法(Pathfinder Algorithm, PFA)[15]受到动物群体运动的启发，模仿动物群体的领导阶层来寻找最佳的食物区域或猎物。每个个体在空间中都有一个位置，种群中的最优位置将被选为领导者，这里我们称种群的领导者为探路者，种群中的其他个体称为跟随者，到寻找猎物或觅食区域时，个体将跟随探路者，则探路者的更新公式如下

其中K表示当前迭代，xi是第i个成员的位置向量，xj是第j个成员的位置向量，R1和R2是随机向量，R1=αr1, R2=βr2，r1和r2是在[0,1]范围内均匀生成的随机变量，α是相互作用系数，取值为α= 1+(2−1)·rand，β是与探路者保持的随机距离，取值为β=1+(2−1)·rand，ε是振动向量，使用如下更新公式

其中u1和u2是在[0,1]的随机数，Dij是两个成员之间的距离，Kmax是最大迭代次数。

3 多根非线性方程组求解的探路者灰狼算法

3.1 探路者灰狼算法(PGWO)

灰狼优化算法和探路者算法从算法结构上讲，两个算法都有领导者和跟随者，灰狼主要由α狼进行引导使其他等级的狼向猎物展开攻击围捕。因此，α狼对应看作是探路者，β狼则是α狼的跟随者，δ狼的位置由α狼、β狼决定，可以看作跟随者。两种算法进行结合在原理上具有一定优势，由于GWO 算法后期收敛速度慢，原因在于狼群主要依据与α、β和δ的距离来判断与猎物之间的距离所导致。而在PFA 算法中，跟随者的更新机制可以有效解决这一问题，具有较好的平衡算法的全局搜索和局部开发的能力。PGWO 算法将保留α狼的更新原则，对其余灰狼的更新将结合跟随者的更新原则对原过程进行修改。这样即保留了全局搜索能力，又提高了局部开发能力，增强探测能力的同时提高收敛速度和精度。

α狼的位置按照GWO 算法中的更新公式(7)、(10)进行更新，β狼作为α狼的跟随者，为最优的跟随者，β狼的位置更新将直接由与α的距离决定，位置更新如下

δ狼作为α和β狼的跟随者，是次优的跟随者，位置更新由α和β，β和δ的距离决定，位置更新如下

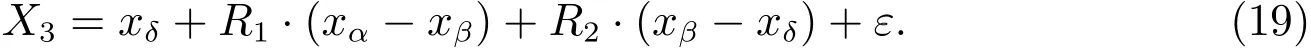
其他灰狼的位置更新如下

其中C、A分别按照公式(5)和(6)进行更新，ε按照公式(17)进行更新。探路者原算法中跟随者的位置由任一位置和最优位置的距离决定的，而改进的GWO 算法中跟随者的位置由最优跟随者和探路者决定，可以提高算法的局部搜索能力，提高搜索精度。

3.2 算法步骤

多根非线性方程组的求解就是将问题转化为最优化问题，由于传统算法的局限性和复杂性，一般群智能算法在多根问题的求解存在求解个数不全以及精度不高的问题。本文提出探路者灰狼算法，相比较原始灰狼优化算法结合了探路者算法的探路者和跟随着的更新机制，并对位置更新机制进行更改，有效提高算法的收敛速度以及搜索精度，具体算法描述如下：

步骤1 参数设置，种群规模N，最大迭代次数Tmax，搜索维度D，搜索范围[lb,ub]以及A、C、ε；

步骤2 初始化种群个体，并计算灰狼个体的适应度值，保存适应度值最好的前三匹狼记为α、β、δ；

步骤3 根据公式(7)和(10)对α狼的位置进行更新，再根据公式(18)和(19)分别更新种群中β、δ狼的位置，根据公式(20)更新当前灰狼位置；

步骤4 根据公式(5)和(6)更新参数A、C，再根据公式(18)更新参数ε；

步骤5 判断是否满足结束条件，若满足输出结果，即为最优灰狼位置，否则返回步骤3。

4 仿真实验与结果分析

为了测试PGWO 算法的多根非线性方程组求解的性能，采用9 个方程组作为测试方程组，并且和其他实验数据加以比较。在对比实验中，为保证算法的公平性，所有的仿真实验实现在CPU 为Intel Core i7-10510u，主频为1.80 GHz，内存为8 GB 的PC 上，采用Matlab R2018(b)进行实现。

实验1 选取参考文献[16]中的方程组1、方程组2，参数设置为：种群规模N=30，最大迭代次数1 000，独立运行30 次，计算其平均值，实验结果如表1。

表1 方程组1、方程组2 的计算结果

方程组1

其中x ∈[0,2]，理论解为x∗=(1.546 342,1.391 174)T, x∗=(1.067 412,0.139 460)T。

由表1 可知，NA 表示未求出的解，对于方程组1，PGWO 算法能求出全部解，比HCS 算法和文献[17]中的AGSO 算法求解精度高，并且求解精度优于原始灰狼优化算法。对于方程组2，AGSO 算法和GWO 算法只能求出两个解，求解不全，PGWO 算法求得全部解并且求解精度优于HCS，说明利用此算法能更大程度地获得问题的解。

实验2 选取文献[16]中的方程组9、方程组10 进行比较分析，为了方便比较，参数设置为：种群个数100，最大迭代次数5 000，Pa= 0.25, F= 0.6, CR= 0.8，每个方程组独立运行50 次，求其平均值，实验结果如表2 和表3 所示。

方程组3

从表2 和表3 可知，方程组3 用本文算法求出的结果比理论值精度高，但x2比HCS 算法的精度略差，与标准GWO 算法和AGSO 算法相比求解精度高。方程组4 的测试结果与理论值、HCS、AGSO 算法比较发现PGWO 算法能求出全部解并且求解精度较高。

表2 方程组3 的计算结果

实验3 选取参考文献[18]中的例1、例4、例5 进行测试分析，以及文献[19]中的F36、F52。参数设置为：种群个数100，最大迭代次数1 000，每个方程组独立运行50 次，求其平均值，实验结果如表4 至表6 所示。

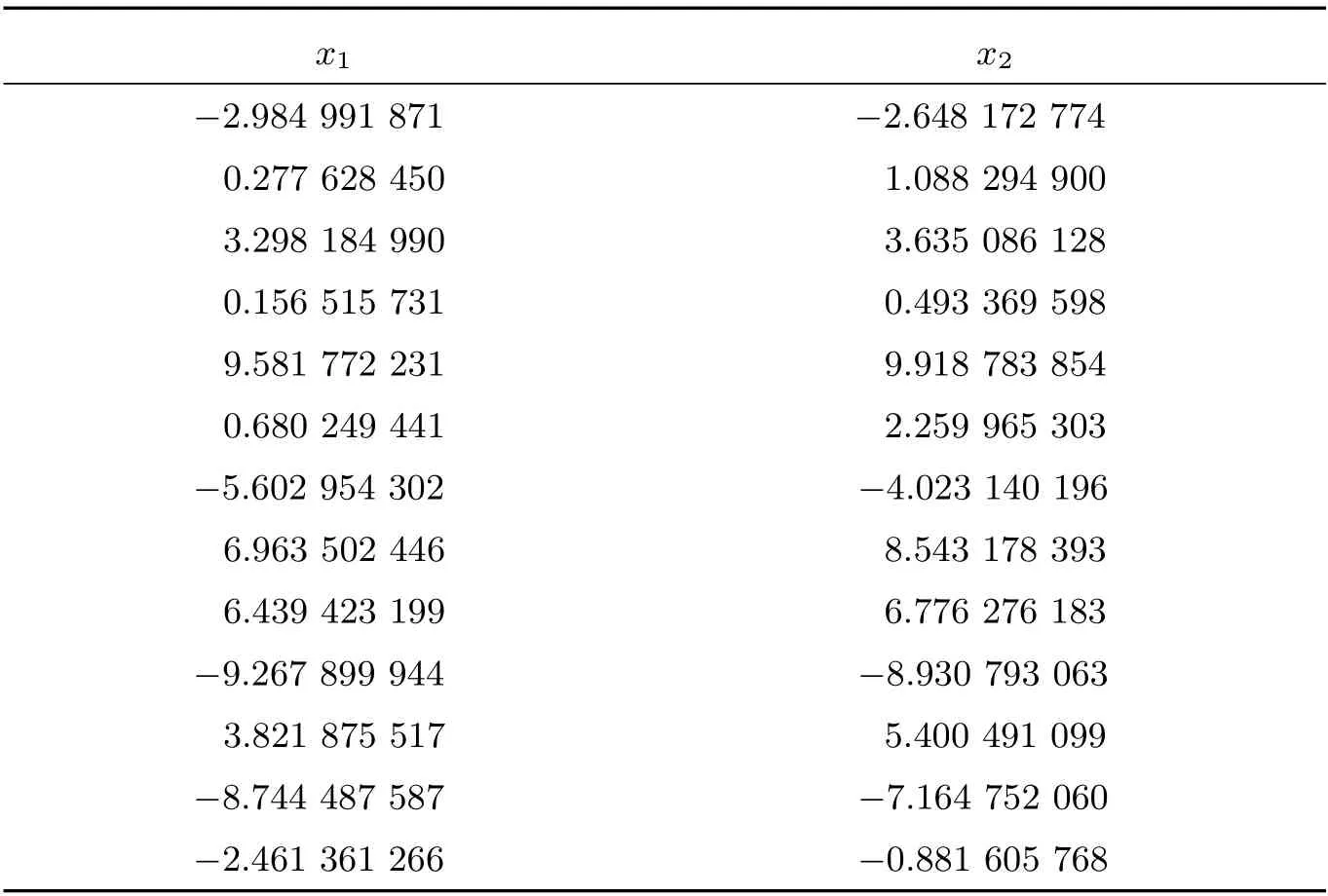
表4 方程组5 的计算结果

表6 方程组7 的计算结果

方程组5

其中xi ∈[−10,10]，该方程有如下13 个解：

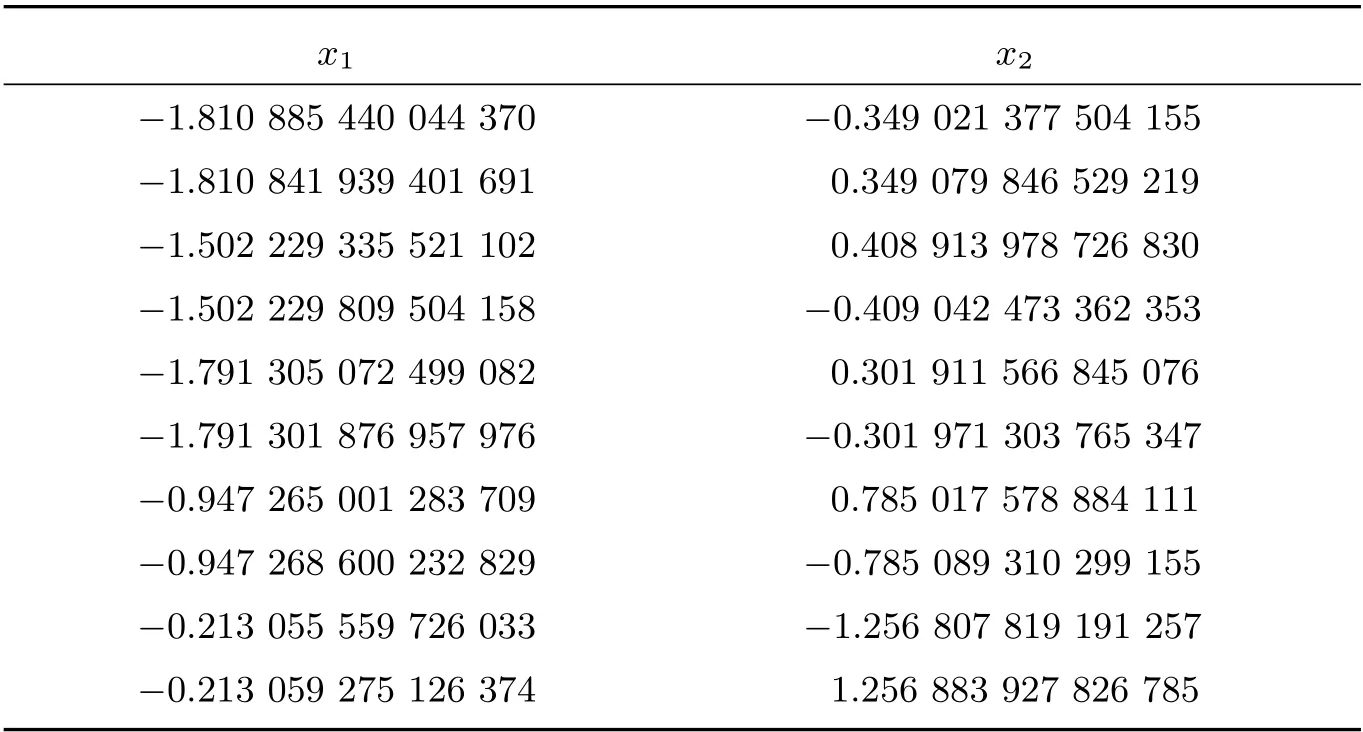
表5 方程组6 的计算结果

方程组7

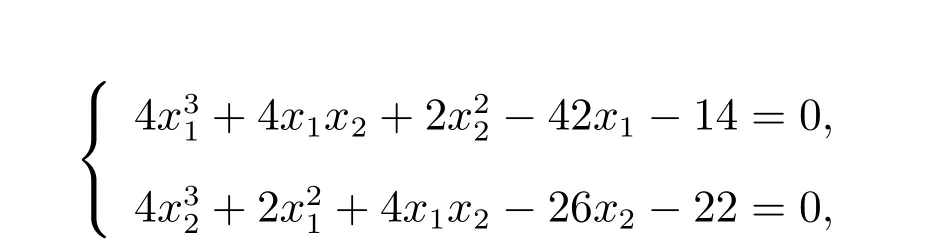
其中xi ∈[−5,5], i=1,2，该方程有如下9 个解：

根据以上方程组可知，方程组5 有13 个解，HCS 算法求出9 个解，AGSO 算法求出8 个解，GWO 算法求出10 个解。方程组6 有10 个解，HCS 算法求出10 个解，AGSO算法求出8 个解，GWO 算法求出10 个解，但求解精度较PGWO 算法稍差。方程组7 有9个解，HCS 算法求出7 个解，AGSO 算法求出5 个解，GWO 算法求出7 个解，对于这三个多根的方程组，由表4 至表6 可知，PGWO 算法可以求出全部解并且求解精度较高，说明该算法在迭代范围内能求出全部解，PGWO 算法在多根非线性方程组的求解问题中具有较强的搜索能力。

方程组8

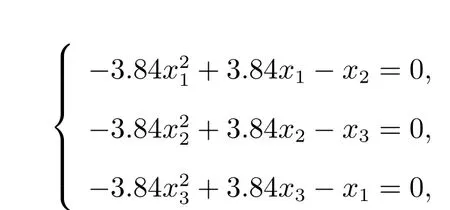
其中xi ∈[0,1], i=1,2,3，该方程有如下8 个解：

方程组8 有8 个标准解，从表7 中数据显示，PGWO 算法求出7 个精度较高的解，而HCS 算法和AGSO 算法均求出6 个解，GWO 算法求出7 个解。方程组9 有15 个标准解，从表8 中数据显示PGWO 算法求出14 个精度较高的解，而HCS 算法和AGSO 算法均求出13 个解，GWO 算法求出14 个解。根据以上8 个多根测试方程组的实验结果可以看出，在求解多根方程组1 至方程组4 时，PGWO 算法的求解性能相对其他群智能算法比较明显，足以说明GWO 算法和PFA 算法融合对多根非线性方程组求解的高效性。对于多根方程组5 至方程组7 的求解，PGWO 能够求出全部解且求解精度较高。但是从方程组8、方程组9 的数据显示，PGWO 算法在求解个别多根的非线性方程组是依然存在求解不完全的问题，该问题也会成为进一步改进的重点。

表8 方程组9 的计算结果

5 结论

本文分析了传统多根非线性方程组求解方法的不足，并提出了一种结合探路者算法中跟随者更新机制的灰狼优化算法。通过9 组测试方程组进行了反复实验，并与其他智能优化算法进行比较分析，最后实验数据表明，本文算法在求解的精度上都具有一定优势，但是对于个别多根非线性方程组的求解存在求解不完全的现象。接下来将针对该算法进行深入研究，并应用到其他领域。