Navier-Stokes/Darcy模型的BDF2 模块化梯度散度稳定格式的数值分析

杨翠平, 王江珊, 贾宏恩

(1. 太原学院数学系，太原 030012; 2. 太原理工大学数学学院，晋中 030600)

0 引言

一直以来，对Navier-Stokes/Darcy 和Stokes/Darcy 模型数值方法的研究得到了广泛的关注。迄今为止，大量的数值格式被提出用来求解这一耦合问题。例如：有限元方法[1]、两层网格法[2–4]、区域分解法[5–7]、边界积分法[8–9]、特征线稳定化有限元法[10]、梯度散度稳定方法[11–12]。然而，梯度散度稳定方法由于稳定项导出的矩阵是奇异的，且对于大的稳定项参数γ会导致求解器故障。为了减弱或克服这些困难，在文献[13]中模块化梯度散度稳定方法被提出用于求解Navier-Stokes 方程，文献[14]中对Navier-Stokes 方程提出了BDF2 模块化梯度散度稳定格式。本文对Navier-Stokes/Darcy 模型提出了BDF2 模块化梯度散度稳定格式，这种格式在保留梯度散度稳定格式优点的同时，更易于操作，且可以有效地避免大的稳定化参数γ对解的非正常影响。

本文的结构如下：第1 节，引入了Navier-Stokes/Darcy 模型和一些相关的符号、函数空间等；第2 节，给出了求解Navier-Stokes/Darcy 模型的BDF2 模块化梯度散度稳定格式并证明了该格式的稳定性；第3 节，给出了误差分析；第4 节，通过数值算例对于所提出方法的有效性进行了验证。

1 Navier-Stokes/Darcy 模型及其相关符号

设在有界区域Ω ∈Rd(d= 2,3)，这里Ω包含两个不重叠的流体区域，分别是自由流体区域Ωf和多孔介质区域Ωp，见图1。假定Ωf和Ωp的边界满足Lipschitz 条件，且

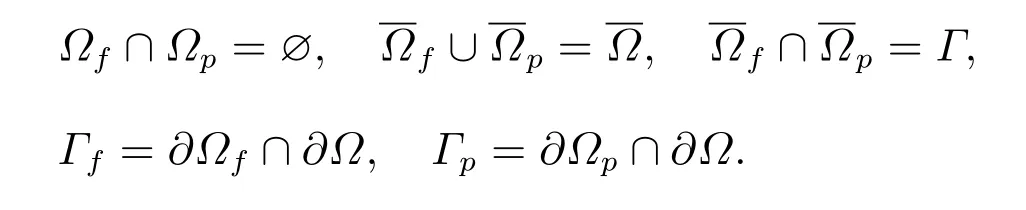
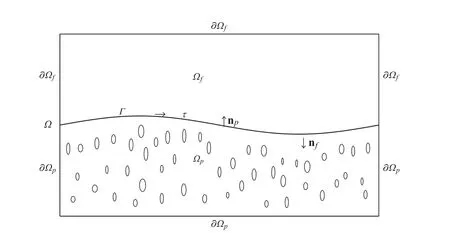
图1 问题区域Ω 及其边界和交界面示意图

自由流体区域Ωf由Navier-Stokes 方程控制

其中u=u(x,t)表示流体的速率，p=p(x,t)表示区域Ωf所受到的压力，f1表示区域Ωf所受到的外力，ν>0 是Ωf流体的粘性系数。

多孔介质区域Ωp由Darcy 方程控制

其中S0是物质的释水系数，up是区域Ωp中的流速，f2是源项，ϕ表示测压水头函数，K 是渗透率张量。假设K=diag(K,··· ,K)，且满足K>0。

通过使用Darcy 定律，(2)式可以整理为如下形式：

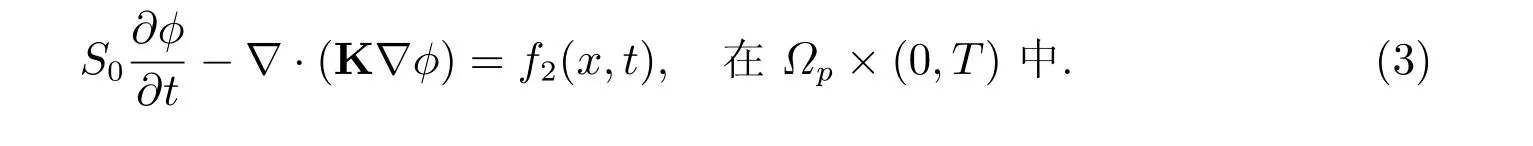
在交界面Γ上，我们考虑特定的交界面条件：质量守恒条件、力的平衡条件和Beavers-Joseph-Saffman(BJS)条件

其中nf和np分别是Ωf和Ωp的单位外法向量，τi(i=1,2,··· ,d −1)是交界面Γ上的单位正切向量，g是重力加速度，α取决于多孔介质的性质并由实验决定。

为便于以后的分析，我们在边界Γf、Γp上引入如下的边界条件

2 全离散格式与稳定性分析

估计不等式(22)右端的每一项如下：

最后，使用引理1，可得到(20)式成立。

3 误差分析

定义投影算子[20]：Ph:(u(t),p(t),ϕ(t))∈Hf×Q×Hp →(Phu(t),Php(t),Phϕ(t))∈Hfh×Qh×Hph。假定(Phu(t),Php(t),Phϕ(t))是(u(t),p(t),ϕ(t))的近似，并且有以下性质

记un、pn、ϕn为时间tn=n∆t处的精确解，并假设精确解满足如下的正则性

引入以下误差

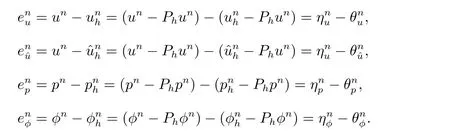
定义1 定义下述的误差

成立。

定理2 在正则性假设条件(25)下，假定β>0，则存在C>0，满足

(27)式、(28)式分别与(16)式、(17)式相减，有

合并两式并使用引理5，有

接下来，利用Cauchy-Schwarz-Young 不等式和引理2，对(31)式右端的每一项进行估计

使用引理2，有

对边界项的估计如下

对非线性项的估计如下

4 数值算例

本节将利用数值算例来验证理论分析，区域Ω由Ωf= (0,1)×(1,2), Ωp= (0,1)×(0,1)和边界Γ=(0,1)×{1}组成，精确解为

实验中参数n、ρ、g、ν、K、S0和α都设为1，梯度散度参数γ= 1, β= 0.2，初始条件、边界条件及稳定项都满足精确解。为了确保实验的准确性，设定h= ∆t，对Navier-Stokes 方程和Darcy 方程分别使用P2—P1 元和P1 元，数值实验结果参见表1 至表3。

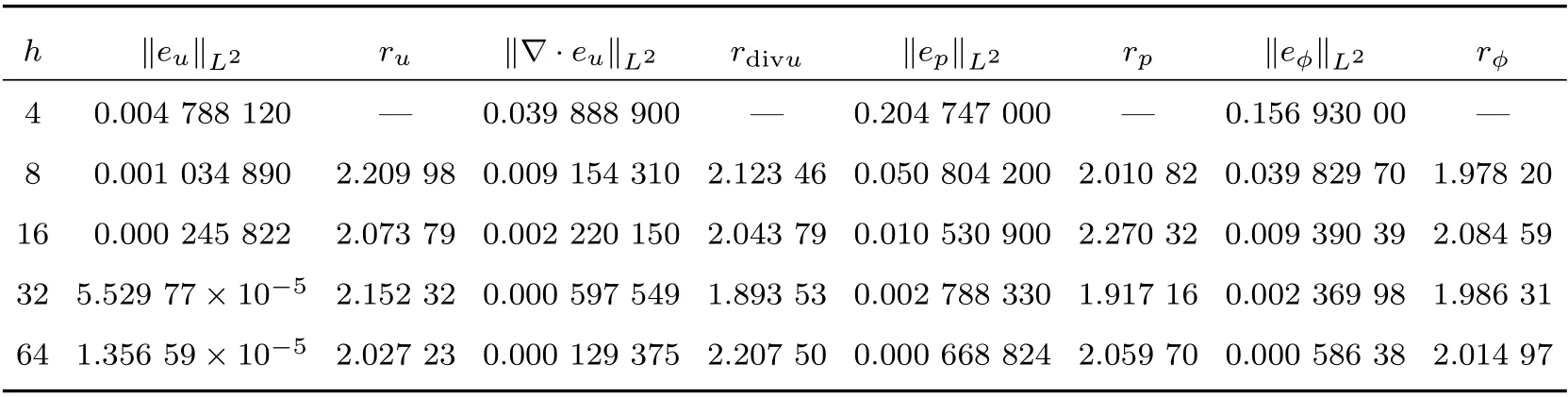
表1 在T =1 时刻，具有L2 范数的标准格式的数值结果

表3 在T =1 时刻，具有L2 范数的BDF2 模块化梯度散度稳定格式的数值结果

来计算收敛阶。通过观察可以发现，梯度散度格式的速度的散度误差要比标准格式的小，特别是BDF2 稳定格式要比标准稳定格式的更精确，所有的数值实验都证实了理论分析的正确性。

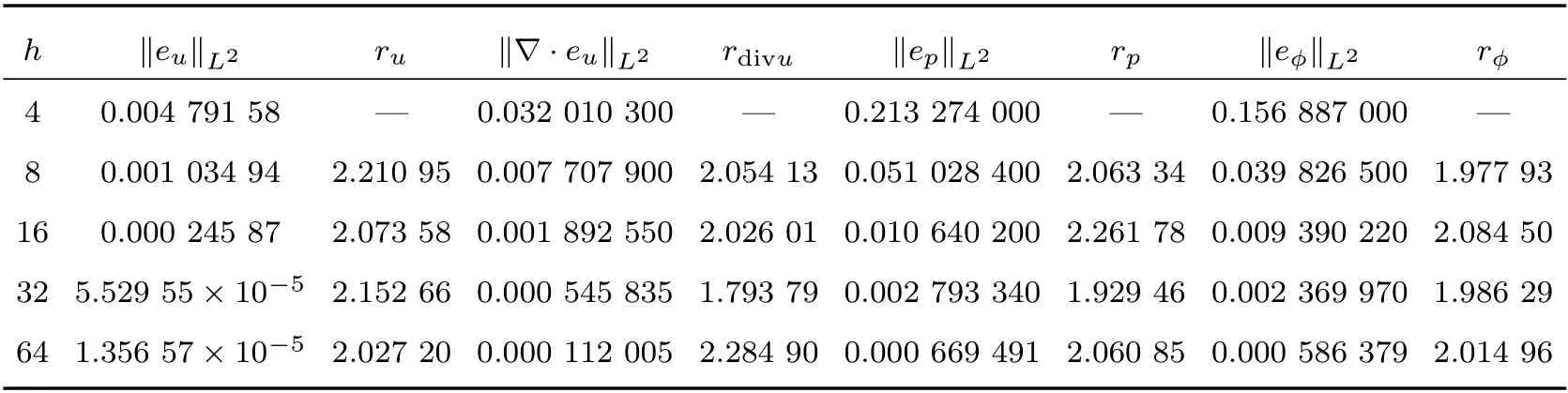
表2 在T =1 时刻，具有L2 范数的标准稳定格式的数值结果