非线性分数阶积分微分方程边值问题正解的存在性

杨晓莹, 贾 梅, 刘锡平

(上海理工大学理学院，上海 200093)

0 引言

近年来，由于分数阶微分方程广泛应用于生物数学、信号识别、化学和工程技术等领域，受到了广泛关注[1–8]。由于边值问题在流体力学、气体湍流、热传导以及电学等许多问题上有着广泛应用[9–10]，微分方程边值问题成为微分方程理论研究中的一个基本问题。因此，对分数阶微分方程边值问题的研究受到学者们的重视[1,11–17]，关于分数阶积分微分方程边值问题正解的研究也取得了许多有意义的研究成果[1,14–17]。

本文研究如下具有两个Riemann-Liouville 分数阶导数项的非线性分数阶积分微分方程积分边值问题

1) 对所有的u,v ∈R, f(·,u,v)均可测；

2) 对几乎所有的t ∈[0,1], f(t,·,·)连续；

3) 对每个r> 0，都存在非负函数Φr ∈Lq[0,1]，使得当|u|,|v|∈[0,r]且几乎处处t ∈[0,1]时，有

上下解方法和单调迭代理论是研究微分方程边值问题解的存在性的有效方法[18–23]。当所研究的问题只含有一个分数阶导数项时，可以通过对原问题定义的上下解获得解的存在性。当微分方程中含有两个或两个以上相互独立的分数阶导数项时，直接定义上下解会遇到诸多麻烦。为了解决涉及两个分数阶导数项的问题直接定义上下解的困难，本文首先通过一个变换，将原问题转化为只有一个导数项的等价形式，再定义等价问题的上下解，利用单调迭代技术建立了原问题正解的存在性与唯一性定理，给出了求唯一正解的迭代格式和误差估计。最后，给出实例说明所得结论的有效性和适用性。

1 预备知识

下面介绍本文所要用到的一些定义和引理。

定义1[1]函数y:(0,∞)→R 的γ>0 阶Riemann-Liouville 分数积分定义为

则(E,//·//)是Banach 空间。

定义3 设u ∈E，若u=u(t)满足边值问题(1)，则称u是边值问题(1)的一个解。若当t ∈(0,1]时，u(t)≥0，则称u是边值问题(1)的一个正解。

本文总假设下列条件成立：

(H1) 存在非负函数b1,b2∈C[0,1]，使得对任意的t ∈[0,1], u ∈R，有

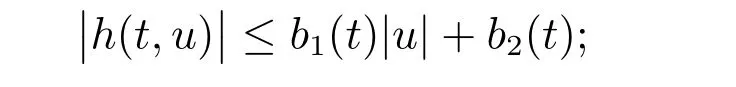
(H2) 存在r>0, ψr ∈L1[0,1]，当|u|∈[0,r]时，使得对几乎处处的t ∈[0,1]，有

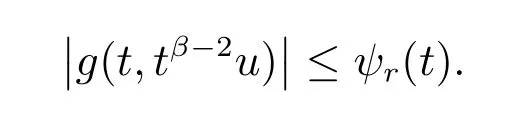
因此，将c1、c2代入(8)式可得，当t ∈(0,1]时，有

同理可证，对任意的t,s ∈[0,1]，有

2 正解的存在唯一性

令P={u:u ∈E,t2−βu(t)≥0, t ∈[0,1]}，显然P ⊆E为一个锥，即对任意的x,y∈E, x ≼y，当且仅当y −x ∈P。于是(E,≼)为半序的Banach 空间。

定义4 如果x ∈P满足

假设：

(H3) 对任意的u1,u2,v1,v2∈[0,+∞)，当u1≤u2, v1≤v2时，对任意的t ∈[0,1]，都有

0≤f(t,u1,v1)≤f(t,u2,v2),0≤h(t,u1)≤h(t,u2),0≤g(t,u1)≤g(t,u2).

定理1 假设条件(H3)成立，边值问题(2)存在一个下解x0∈P和一个上解y0∈P，且满足x0≼ y0。记序区间D= [x0,y0] ={u ∈P|x0≼u ≼y0}，则边值问题(1)在D中存在最小正解和最大正解。

故可得函数列{xm}，且xm=xm(t)(m= 1,2,···)是边值问题(2)的下解，xm−1≼xm，所以{xm}是单调增序列。

类似，以y0=y0(t)作为迭代的初始函数，则有

因为G(t,s)、G1(t,s)在[0,1]×[0,1]上连续，则t2−βG(t,s)、t2−βG1(t,s)在[0,1]×[0,1]上一致连续。因此，对任意的ε> 0，存在δ> 0，使得对所有的t1,t2,s ∈[0,1]，当|t1−t2|<δ时，有

所以序列{xm}是等度连续的。类似可证明，序列{ym}是等度连续的。

由Arz´ela-Ascoli 定理可知，序列{xm}和{ym}是相对列紧的。而序列{xm}和{ym}又是单调的，则存在x∗和y∗，使得

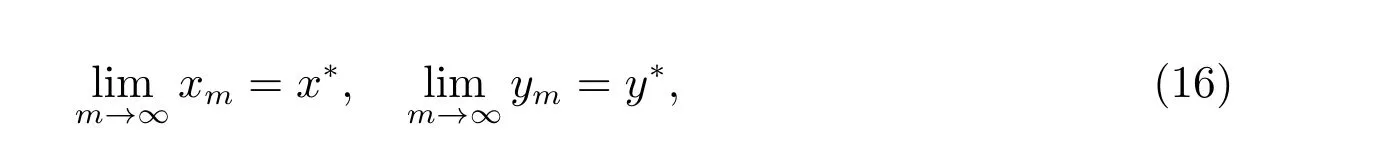
故有x0≼x∗≼y∗≼y0。

4) 证明x∗和y∗是边值问题(1)的解。由(13)式及Lebesgue 控制收敛定理，可得

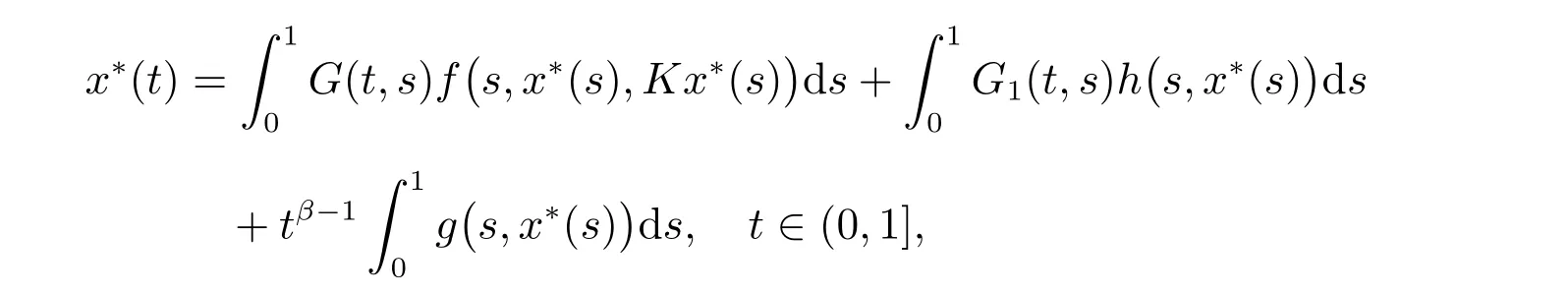
所以x∗是积分方程(5)的解。由引理3 及引理4 可得，x∗是边值问题(1)的解。同理可得，y∗也是边值问题(1)的解。

5) 证明x∗和y∗分别是边值问题(1)在D中的最小正解和最大正解。设z∗∈D是边值问题(2)的解，则x0≼z∗≼y0。

假设xm−1≼z∗≼ym−1，所以对任意的t ∈(0,1]，有xm−1(t)≤z∗(t)≤ym−1(t)。根据引理5 及假设(H3)，可得

即xm ≼z∗。

类似可证得z∗≼ym。因此，运用数学归纳法，可得xm ≼z∗≼ym(m=0,1,···)。

令m →∞，可得x∗≼z∗≼y∗，所以x∗是边值问题(1)在D中的最小正解，y∗是边值问题(1)在D中的最大正解。

综上所述，定理1 得证。

定理2 假设定理1 的条件成立，并且满足条件：

(H4) 存在常数M1,M2,M3,M4>0，使得对任意的v1,v2∈[x0,y0]，当v1≼v2时，对任意的t ∈(0,1]，有

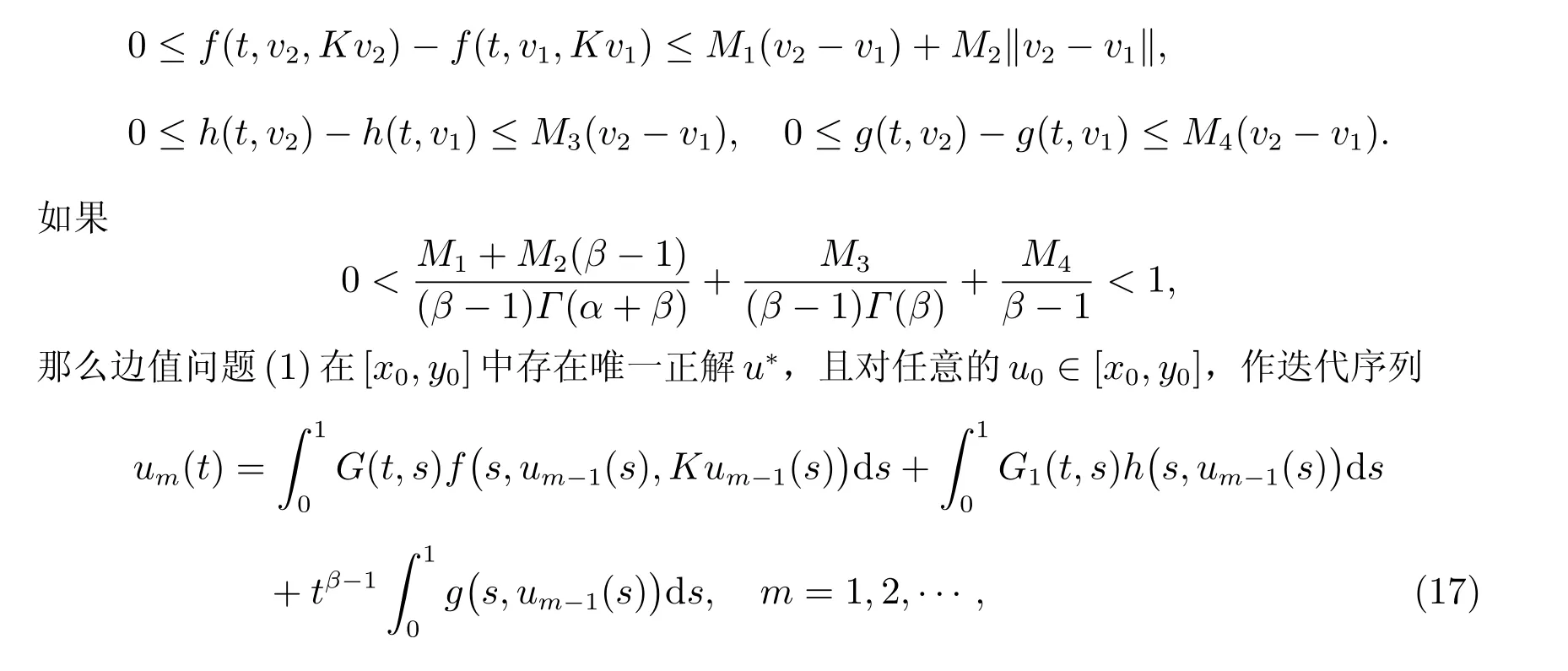
对任意的u0∈[x0,y0]，则x0≼u0≼y0。由(17)式和(H3)，利用数学归纳法易得xm≼um ≼ym，则对任意的t ∈[0,1]，有

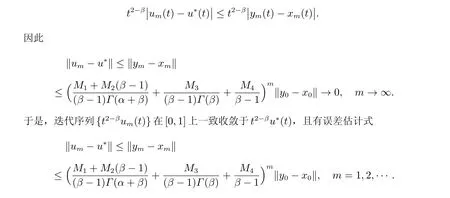
综上所述，定理2 得证。

3 应用举例

为了说明我们所得结论的有效性和适用性，考虑下列非线性分数阶积分微分方程边值问题

故易知f满足Lq-Carath´eodory 条件。

于是，假设(H1)、(H2)成立。

根据引理3，边值问题(18)等价于边值问题

所以x0、y0分别是边值问题(19)的下解和上解，且满足x0≼y0。

对任意的u1,u2,v1,v2∈[0,+∞)，当u1≤u2, v1≤v2时，对任意的t ∈[0,1]，有

所以满足(H3)。

由以上讨论，定理1 的条件成立。由定理1 可得，存在x∗,y∗∈P，使得x∗是边值问题(18)在D中的最小正解，y∗是边值问题(18)在D中的最大正解。另一方面，取

当迭代10 次时，误差不超过0.08，而迭代20 次时，误差不超过0.000 18。