解析几何中“非对称式”问题的解题策略——解析几何中的一类开放性试题探究

张 军

(辽宁省大连市第二十四中学)

数学教育承载着落实立德树人根本任务、发展素质教育的功能.高考评价体系确立了高考考查中要增强试题的灵活性和开放性,改变相对固化的试题形式,减少死记硬背和“机械刷题”现象.开放性试题是与封闭性试题相对应的概念,一般来说,封闭性试题具有确定的条件、方法和答案,而开放性试题是指围绕某一个核心主题,提供一定的核心材料,要求学生就试题设问进行深层分析和开展探究的一种命题形式,即题目的条件是不完备的、解题策略是多种多样的.数学开放性试题的核心是考查学生综合运用所学数学知识解决问题的能力,从而激发学生独立思考和创新的意识.

解决开放性问题难在要求学生的思维要多向辐射,它没有固定的解题模式.由于开放性试题所提的问题要么是条件不充足或条件是多种多样的,要么结论被隐去或不确定,要么只是给出一定的问题情境,其条件、解题策略和结论都需解题者从情境中寻找和设定,收集其他必要的信息,才能着手解题,所以它的解答有的是没有固定的、现成的模式可循,有的是答案可能易于被发现,但是求解过程中往往需要学生进行主动思考,从多个角度进行探究.这一探究过程往往能够拓宽和深化解题思维过程,揭示解题过程的思维途径,培养学生的探究思维,提高学生的数学核心素养.

一个含有若干个变量的多项式中,如果任意交换两个变量的位置,多项式不变,则称这样的多项式关于这两个变量是对称的,否则称为非对称式.在解析几何中,当直线和曲线相交时经常会涉及与交点有关的开放性试题.对于这类试题,在求解过程中如果相应的目标式子是关于两个交点的横(或纵)坐标x1,x2(或y1,y2)的和或积的式子,这个式子往往是关于x1,x2(或y1,y2)对称的,这时只要把直线方程和曲线方程联立,利用根与系数的关系即可解决问题.然而在有的时候,往往也会出现相关的目标式子不是简单的关于x1,x2(或y1,y2)的和或积的对称式子,也就是出现了非对称的形式,此时就不能通过根与系数的关系进行简单的代换来解决,下面举例介绍如何解决这类开放性试题.

1 多解探究

2 巩固练习

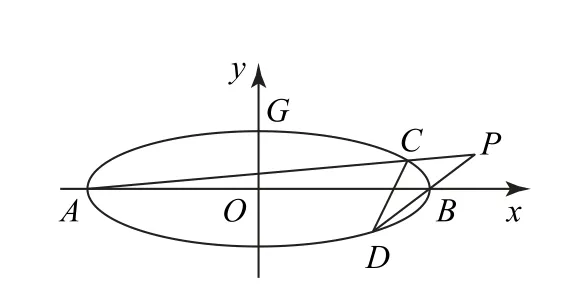
图1

图2

练习3 如图3 所示,已知点F1(－1,0),F2(1,0),以线段F2G为直径的圆内切于圆O:x2＋y2＝4,点G的轨迹为F.

图3

(1)求点G的轨迹E的方程;

(2)若轨迹E与x轴的左、右两个交点分别为M,N,过定点P(－3,0)的直线l与轨迹E交于R,S两点,设直线MR与NS交于点T.试探究点T是否在一条定直线上.若是,求出此定直线方程;若不是,说明理由.

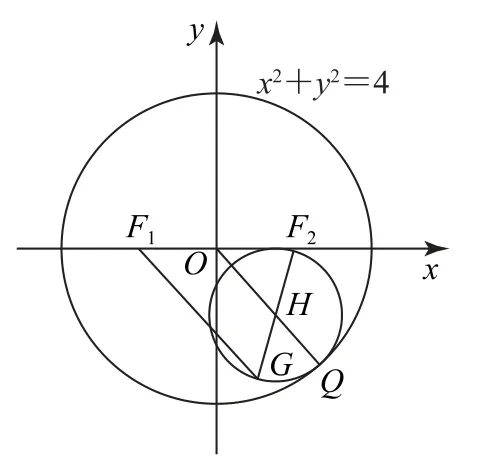
图4