关注解题方法上的类比

杨海军

(甘肃省民乐县第一中学 734500)

灵活运用解题思维上的“类比”观点，往往可帮助我们巧妙借用熟悉的解题思路、方法迅速求解相关数学问题，令人倍感解题成功的喜悦.显然，有意识地去关注解题方法上的类比，有利于帮助我们创新思维能力，启迪数学智慧，提升数学核心素养.

1 考查等比数列前n项之积

例1设an是等差数列，其前n项之和为Sn，则利用“倒序相加法”可求得2Sn=na1+an.运用类比推理的思想可知：设bn是等比数列，其前n项之积为Tn，则利用“____”可求得____.

解析由于等差数列an中的特性“若n+m=p+q，则an+am=ap+aq”可类比为等比数列bn中的特性“若n+m=p+q，则bn·bm=bp·bq”，所以类比推理知：在等比数列中，应该利用“倒序相乘法”.

因为Tn=b1b2…bn,Tn=bnbn-1…b1，

所以将这两个等式相乘，得

又易知b1bn=b2bn-1=…=bnb1.

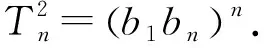
评注根据等差、等比数列中的相关特性，借助类比思维可知，要得到等比数列中前n项之积，需要利用“倒序相乘法”.

2 考查一元三次方程根与系数的关系

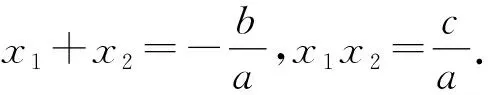
解析由题设得

ax3+bx2+cx+d=a(x-x1)(x-x2)(x-x3)=ax3-ax1+x2+x3x2+ax1x2+x2x3+x1x3x-ax1x2x3，

从而比较两边系数，可得

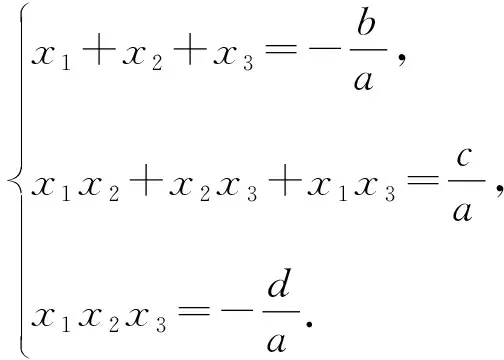
这就是一元三次方程根与系数的关系．

评注本题主要类比解题技巧——先将多项式分解因式、展开，再利用多项式与多项式相等的充要条件.

3 考查平面的方程

例3平面内，直线的法向量是指与直线垂直的非零向量，根据求动点轨迹方程的思维方法，我们可得到法向量为n=(1,-2)，且经过点A(-3,4)的直线方程是1×(x+3)+(-2)×(y-4)=0，整理可得x-2y+11=0.类比该解题方法，在空间直角坐标系中，法向量为n=(-1,-2,1)，且经过点A(1,2,3)的平面方程是____.

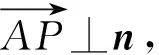
所以1×(x+3)+(-2)×(y-4)=0.

化简,得x-2y+11=0.

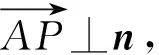
所以(-1)×(x-1)+(-2)×(y-2)+1×(z-3)=0.

从而整理可得x+2y-z-2=0.

因此，可知所求平面方程为x+2y-z-2=0.

评注本题求解需要先理清平面内所给直线方程的求解过程(本质是灵活运用了数量积的坐标运算)，再由平面到空间，利用“类比”思维，即可顺利求解所给平面的方程.

4 考查数列求和

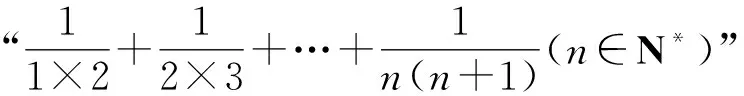
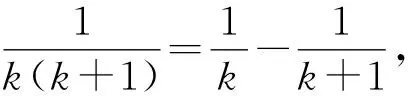
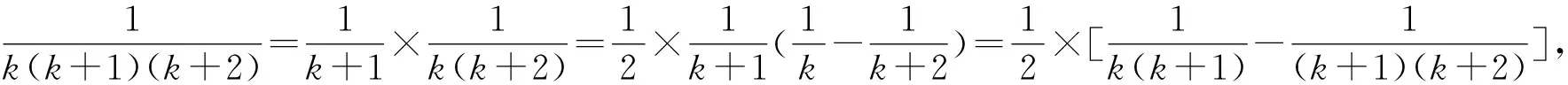
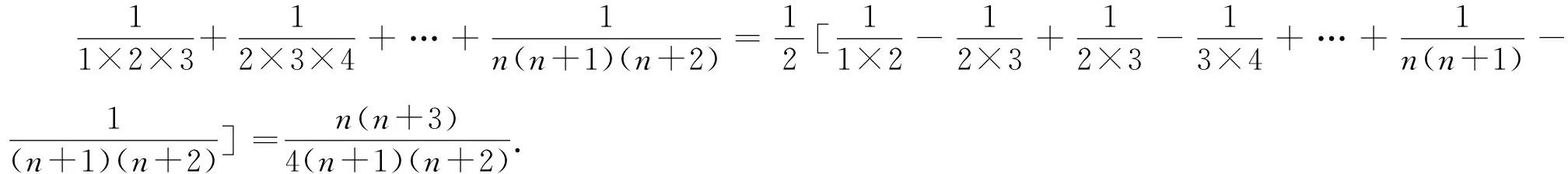
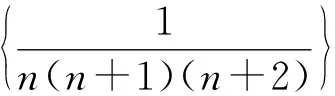
5 考查证明恒等式

例5请看以下例题及其证明过程.

例题：已知α是方程2x+x=3的一个根，β是方程log2x+x=3的一个根，求证：α+β=3.

证明：设函数fx=2x+x，

则由题设得fα=2α+α=3，

flog2β=2log2β+log2β=β+log2β=3，

所以fα=flog2β.

又函数fx在R上单调递增，从而α=log2β.

故α+β=log2β+β=3.

试运用类比推理的思想，求解如下问题：

已知α是方程2x·x=3的一个根，β是方程log2x·x=3的一个根，求证：αβ=3.

证明设函数fx=2x·x，

则由题设得fα=2α·α=3，

flog2β=2log2β·log2β=β·log2β=3，

所以fα=flog2β.

又易知α>0,β>0，且函数fx在0,+∞上单调递增，从而必有α=log2β.

故所求αβ=log2β·β=3.

评注本题首先要从所给例题的证明过程中找到解题方法(先构造函数，再利用函数的单调性求解)，经过如此探寻就获得了求解所给问题的证明思路.

6 考查求代数式的取值范围

例6请认真学习以下典例及其完整的解析过程.

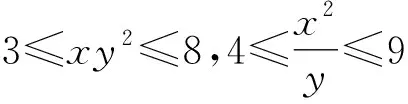
解答：易知x>0,y>0.对已知不等式两边同时取对数，得

lg3≤lgx+2lgy≤lg8,lg4≤2lgx-lgy≤lg9.

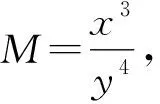
lgM=3lgx-4lgy

=-(lgx+2lgy)+2(2lgx-lgy)

∈[-lg8+2lg4,-lg3+2lg9]=[lg2,lg27].

所以M∈[2,27].

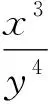
试借助类比推理思维，解答如下数学问题：

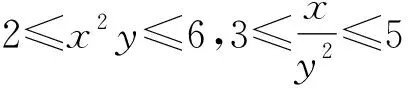
解析由已知可知x>0,y>0，所以对题设不等式两边可以同时取常用对数，即得

lg2≤2lgx+lgy≤lg6,lg3≤lgx-2lgy≤lg5.

设M=x3y4，则两边同时取对数，可得

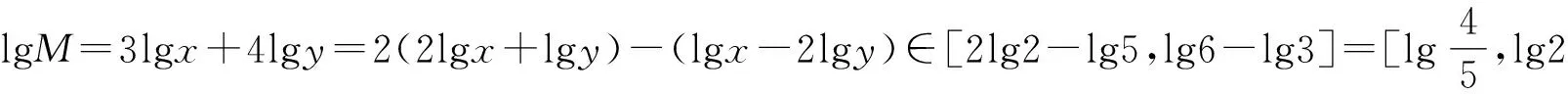
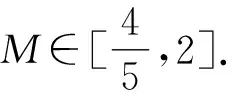
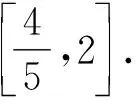
评注本题主要类比解题方法——借助“取对数”变形(多次灵活运用)以及“线性表示”，可巧求目标代数式的取值范围.

总之，通过上述归类举例解析可知：在解题过程中，灵活借用“类比”思维，往往可获得目标问题的巧思妙解，有利于帮助我们拓宽解题思维.一言以蔽之，在探寻解题思路方面，可将“类比”思维看作是一种比较重要的数学思想.