由递推式巧求通项的几种常用策略

刘 瑛

(甘肃省陇南礼县第一中学 742299)

由递推式求数列的通项，是近年高考数学中的一个常考题型，故需要引起我们的高度重视.基于此，本文拟通过归类解析的形式加以具体说明，旨在帮助同学们掌握常用的解题策略，进一步提高解题思维能力，进而提升数学运算与逻辑推理方面的数学核心素养.

1 利用对应恒等式，巧求通项

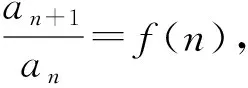
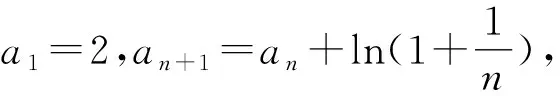
A.2+lnnB.2+(n-1)lnn

C.2+nlnnD.1+n+lnn

解析由已知，得

所以当n≥2时，

an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1

=2+lnn.

又易知当n=1时上式也成立.

于是可得an=2+lnn(n∈N*).故选A.

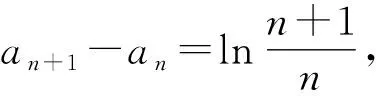
故选A.

2 通过构造等差数列，巧求通项

当题设条件中给出数列满足的递推关系式时，可在灵活变形的基础上，借助“局部整体化”的观点加以思考，有利于帮助我们构造等差数列，并结合等差数列的通项公式解决问题.

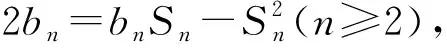
所以当n≥2时，

所以2Sn-1-2Sn=SnSn-1.

又由b1=1易知Sn≠0(n∈N*).

从而对上式两边同时除以2SnSn-1,得

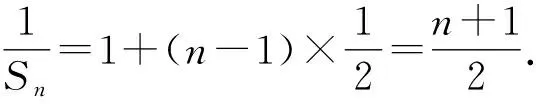
评注(1)本题变形的关键在于消去“bn”，同除以“2SnSn-1”；(2)构造等差(等比)数列之后，就要充分运用等差(等比)数列的通项公式加以分析.

3 通过构造等比数列，巧求通项

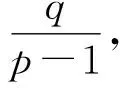
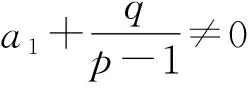
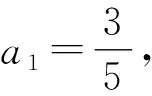
所以两边取倒数变形，得

然后两边同时加-1,得

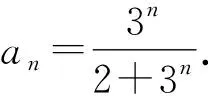
4 通过构造常数列，巧求通项

根据题设给出的数列递推式，如果实施适当的变形，可得到形如f(n)=f(n+1)的递推式，那么可获得数列{f(n)}就是一个常数列，然后再根据f(n)=f(1)即可顺利解题.

例4 在数列{an}中，a1=1，且前n项和Sn满足nSn+1-(n+3)Sn=0(n∈N*)，求数列{an}的通项公式.

解法1因为nSn+1-(n+3)Sn=0，

所以nSn+1=(n+3)Sn.

故n(n+1)(n+2)Sn+1=(n+1)(n+2)(n+3)Sn.

再变形可得

因此，当n≥2时，

an=Sn-Sn-1

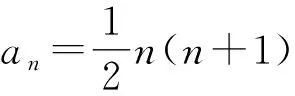
解法2因为nSn+1=(n+3)Sn，

所以(n-1)Sn=(n+2)Sn-1(n≥2).

于是，两式作差，得

当n≥2时，nan+1=(n+2)an.

又易知当n=1时，上式也成立.

所以nan+1=(n+2)an(n∈N*).

从而，可知

n(n+1)an+1=(n+1)(n+2)an.

评注上述解法1实施变形的关键在于对递推式nSn+1=(n+3)Sn两边同乘以“(n+1)(n+2)”， 而解法2实施变形的关键在于对递推式nan+1=(n+2)an两边同乘以“n+1”.此外，需要关注从“局部整体化”的角度去充分理解、认识如何构造常数列.

综上，只要我们真正理解、掌握了以上几种常用策略，那么根据数列递推式求数列通项时，就能做到胸有成竹、游刃有余.值得特别提醒的是：对数列递推式实施适当的变形，是灵活运用常用解题策略，进而顺利破解目标问题的关键所在.