巧借气体虚拟态化解变质量难题

郭公礼

(新疆维吾尔自治区乌鲁木齐市第一中学 830000)

理想气体的变质量问题，可根据不同情况分别使用克拉伯龙方程、理想气体状态方程、气体实验定律以及密度公式，分态方程等等进行求解，由于处理方法多种多样，处理技巧各不相同，应用公式多且灵活多变，对于大多数学生来说掌握起来还有一定难度，能不能找到一种通用方法，让学生易学、易懂、易掌握呢？下面分类介绍巧借虚拟状态，求解气体变质量问题的通用方法.

1 漏气问题

例1有一容积是10L，内装有1.80kg的医用氧气瓶.使用前，瓶内氧气压强为140atm，温度为37℃.当给患者输氧以后，发现这个氧气瓶瓶内氧气压强只剩了50atm，此时温度也降为27℃，试求这位患者消耗的氧气的质量.

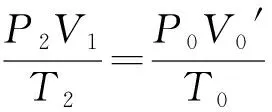
点评解决变质量问题的关键就是把两种不同状态的气体都转化为同一温度，同一压强的气体虚拟态，而且虚拟态的压强与温度可以随意选取，这样只要算出两种虚拟态的体积比，就很容易求出质量比.比起使用密度公式，这是学生最容易听懂且最容易掌握的方法，可以帮助学生理解问题的本质，虽然不是最简便的运算步骤，但是思路简单清晰，能达到一教就会，一练就对的目的，真正做到以不变应万变.

2 分装问题

例2 新型冠状病毒肺炎是一类传染性极强的急性传染病.当前，新型冠状病毒奥密克戎新变异株传染性更强，防控形势仍然严峻.该病主要发病位置在肺部，表现为呼吸困难等，因此治疗过程中有些患者急需进行吸氧.已知某钢瓶容积180L，在室外测得其瓶内氧气压强为4×106pa，环境温度为-23℃，现在先将其移至室内静置(钢瓶的热胀冷缩可以忽略不计)，待温度与室内相同时，将其对容积5L内部气压为2×105pa的小钢瓶分装，分装后每个小钢瓶压强为2×106pa，已知医院病房内温度27℃且最多可分装多少瓶小钢瓶供病人使用？(假设分装过程中大小钢瓶温度均保持不变).

答案：56.

点评解决此题的关键就是把被分装的对象和分装对象的不同状态的气体都转化为同一温度，同一压强的气体，虽然虚拟态压强与温度可以随意选取，但为了简化，一般选取题目中已有压强与温度；然后利用质量守恒即总体积守恒即可解决分装问题.在不用克拉伯龙方程等超纲知识的前提下，构建统一的模式解法，学生更易于上手，只要稍加练习即能熟练.

3 充气问题

例3 2021年11月，王亚平从天和核心舱节点舱成功出舱，成为中国首位出舱行走的女航天员，标志着中国女航天员首次实现“太空漫步”．同时，王亚平身着的新舱外航天服也在首次亮相．在核心舱内时，航天服内气压为1.0×105pa，所充气体体积为2L，由于舱外气压低，航天服内气体体积会膨胀，变为4L，设航天服内气体的温度不变，将航天服视为封闭系统，其内部气体视为理想气体．若开启航天服的充气阀门，向航天服内充入同种气体，保持航天服内气体体积为4L，使航天服内的气压缓慢恢复到0.9×105pa，则需补充压强为1.0×105pa的等温气体多少升？

解析由于温度相同，只要转化为压强相等，利用总体积守恒的原理即可解决，设虚拟末态压强P0为1.0×105pa，把末态(P1、V1)(即航天服4L气压缓慢恢复到0.9×105pa)，转化为虚拟态的体积V0，由等温公式：P1V1=P0V0得V0=3.6L,显然需要补充ΔV=1.6L.

点评分装问题与充气问题互为相反的过程，本质上属于同一问题.在温度相同的条件下，利用等温的规律求出虚拟态的体积，再利用质量守恒即体积守恒即可顺利解决此类问题.

4 抽气问题

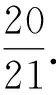
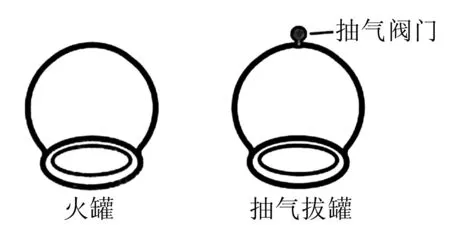
图1

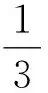
例5 如图2所示，用一体积为ΔV的小型活塞式抽气机对体积为V0的容器A中的气体进行抽气.已知容器A中初始的气体压强为p0，设抽气过程中气体温度均保持不变．求抽气机抽动n次后，容器A中剩余气体的压强pn.

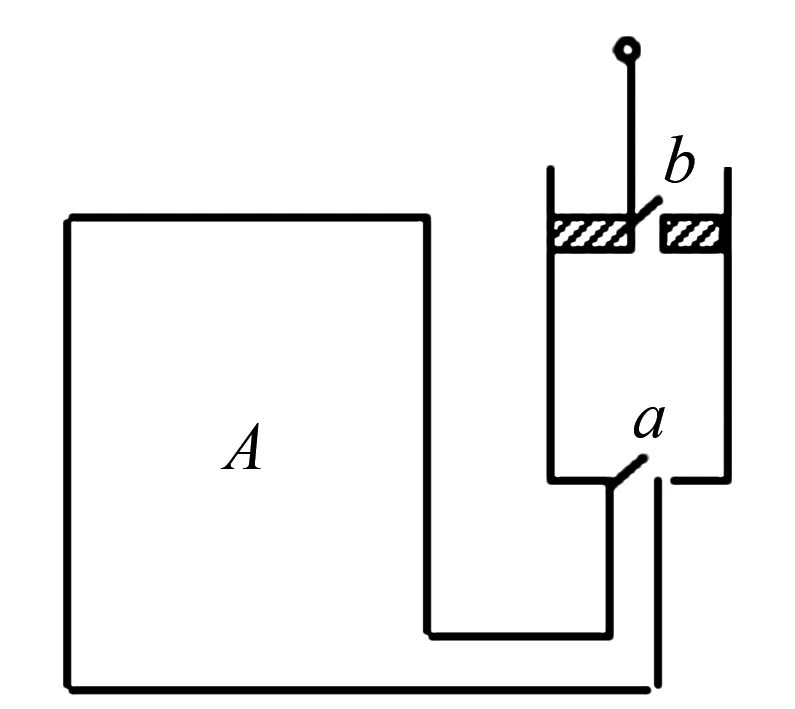
图2

点评利用连续的虚拟态进行递推是解决连续抽气的有效方法.

5 混合问题

例6 如图3所示，两容积相同的哑铃型容器A、B，用体积可以忽略的细长直导管相连，初始时A、B均封入压强为p，温度为T的相同理想气体，现仅对左侧气体加热，使A内温度升温至T′，右侧容器B内气体温度始终为T.求稳定后A容器的气体压强.

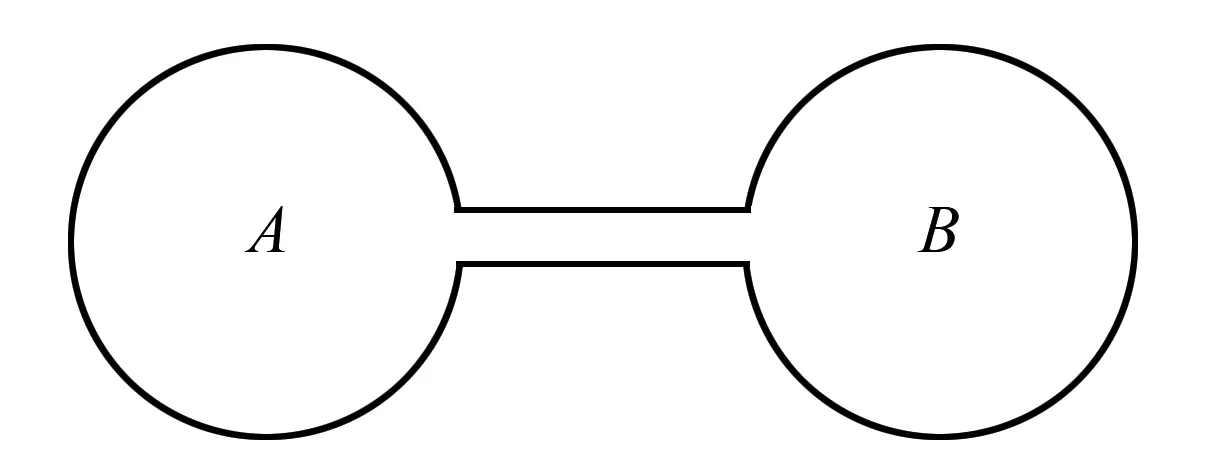
图3

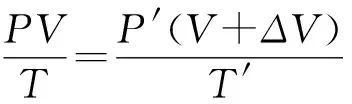
点评对于需要混合的气体A、B先当成一个整体，运用气体状态方程统一转化特定的虚拟状态C，然后对虚拟状态C进行“分装”即可解决.方法一则是先把A转化为特定的虚拟状态D,把D分成终态A′、B′两部分，把B′与B两部分气体利用“充气”原理即可解决.方法二叫“先整体后隔离”，方法一叫“先隔离后整体”.

总之：所谓运用虚拟状态解题，本质上是把克拉伯龙方程(PV=nRT)中的nR用统一的压强、温度和虚拟出一个新体积来表达，再利用质量守恒即虚拟的新体积守恒来解题,而所谓气体变质量问题就变成了虚拟态体积的聚散问题.这有利于学生把握问题本质，找到统一解法，提升学生的学科素养.