风电场道路优化设计算法及应用

杨奎滨杜昊天王其君刘 平

(东方电气风电股份有限公司,四川省 德阳市 618000)

0 引言

为应对日益严重的环境污染和能源短缺问题,无污染、可再生的风能已成为世界各国开发利用的重要对象[1]。面对竞争日益激烈的风力发电市场,降本增效至关重要,因此风电场优化成为研究热点。通过合理布局降低场内道路投资成本,优化场内道路成本占比,是风电场优化的重要组成部分。作为道路优化的先决条件,合理的风电场机位将直接影响道路优化的效果。同时,场内道路优化与风电场机位布局优化之间也不是互相独立的,增加风机之间的间距可减小尾流效应和提升发电量,但会造成道路成本增加,土地成本也会相应地增加,考虑多种因素进行联合优化势在必行。在当前运营的风电场中,因尾流效应造成的风机功率损失可达到20%,寻找合适的机位布局以减小尾流损失对提升风电场的经济效应同样具有重要意义[2]。

由于问题的复杂性,目前业界多采用元启发式算法或随机优化方法来求解缺省风电场布局优化问题[3],很少会采用数学规划方法进行优化[3-5]。与元启发式算法或随机优化方法相比,数学规划中使用的分支定界法是一种精确的算法,当最优松弛解与最优可行解之差与最优可行解之比为0时,可以求出当前问题的绝对最优解,该方法具有能够实时输出当前找到的解与绝对最优解之间的距离范围的优点[6]。因此,如果能将问题建模为目标函数和约束形式,并使用数学规划求解器求解,那么通常会得到比遗传算法这样的元启发式算法更好的结果[7]。在对使用数学规划方法优化风电场布局的探索中,Turner等使用Jensen尾流模型提出了一种新的风电场布局优化的数学规划方法,该方法没有考虑尾流叠加区域面积的影响,与实际问题不符。此外,其对风电场的布局优化问题进行了不等价的简化,即对模型进行线性化后进行求解,会进一步降低计算结果的准确性[4]。Archer等利用Jensen尾流模型定义了表示2个风电机组之间干扰的风强干扰因子,并将风强干扰因子应用于建立风电场布局优化的混合整数线性规划模型。但该模型不能正确反应尾流区域速度的变化,使得所建模型与原问题不符[5]。

针对以上问题,本文将基于Jensen尾流模型的风电场布局优化问题建模成目标函数及约束的形式,并考虑尾流叠加区域面积的影响,使用遗传算法与数学规划法进行求解。旨在提出一种基于软件算法的风电场场内道路-机位排布联合自动优化方法,为风电场设计提供参考。

1 风电场模型

1.1 Jensen 尾流模型

在优化风电场的位置布置时,需要计算各种位置布置中的风电机组功率,其中功率的计算需要使用尾流模型来评估风轮的风速。本节介绍了优化过程中用于评估尾流损失的尾流模型。其中,单风机尾流模型用于评价单风机尾流区域的风速,叠加模型结合单风机尾流模型用于评价多风机尾流区域的风速。

Jensen模型[8]是最著名的一维尾流模型之一(如图1 所示),是由丹麦国家实验室的Jensen 于1983年基于尾流场初始半径为风轮半径、尾流场横截面半径呈线性增长、尾流区域内横向剖面的速度是均匀的这3个假设提出的,适用于安装在平坦地形上的风机。

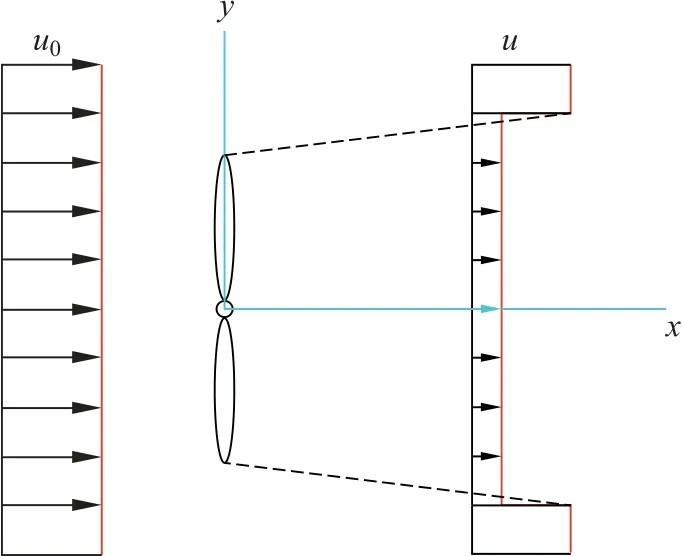
图1 Jensen尾流模型示意图Fig.1 Schematic diagram of the Jenson wake model

Jensen尾流模型的推导原理是控制体内动量守恒。将控制体取为风轮盘后至尾流下游处某一位置的圆柱形区域,流过控制体截面左端的空气向下游流动时因不受外力作用而动量守恒,用方程表示为

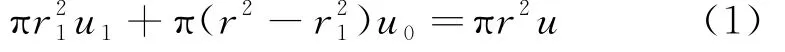
式中:r1为风轮盘面后尾流初始半径;u1为风流经风轮盘面后的风速;r为尾流下游距离风机x处的尾流半径;u0为入流风速;u为尾流下游尾流风速。

根据叶素动量理论,可以求得风轮盘面后尾流初始速度u1和尾流初始半径r1:

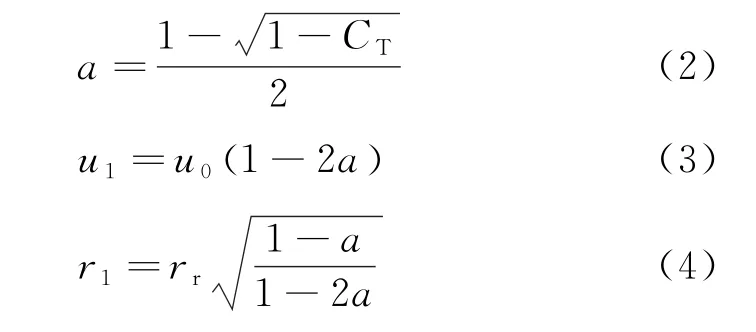
式中:a为轴向诱导系数;CT为推力系数;rr为风轮半径。

假设尾流呈线性膨胀,可以求得尾流下游处距离风机x处的尾流半径r为

尾流扩张系数k由经验公式确定:

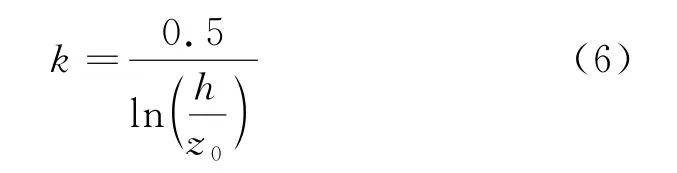
式中:z0为粗糙度系数,一般平坦地形地面粗糙度系数设为0.3,海面粗糙度系数设为0.0002。

将式(3)(5)代入式(1)即可得到尾流下游处距离风机x处的尾流速度u:

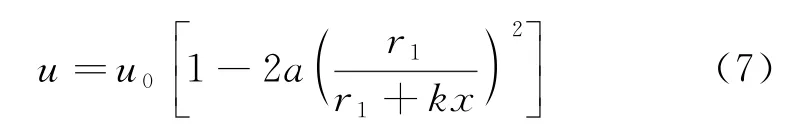
本文引入Katic提出的平方和叠加模型[9],即假设多风机作用下尾流动能损失的平方和等于风机分别作用下尾流动能损失的平方和叠加,即

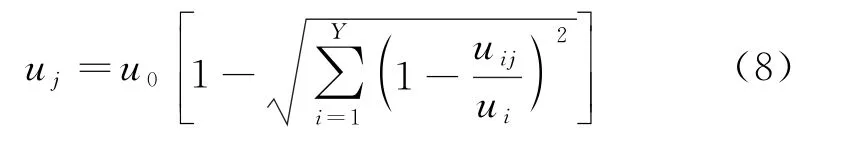
在平方和叠加模型里考虑叠加面积的影响,则有

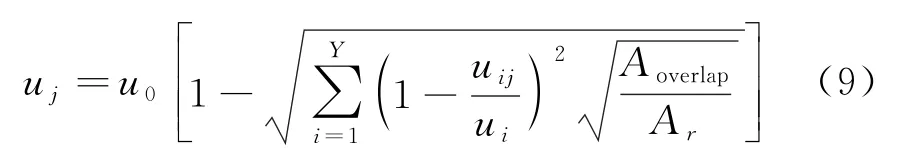
式中:uj是待求风机j处风速;u0是风电场来流风速;uij是受风机i尾流影响下风机j处风速;ui是风机i处风速;Aoverlap是尾流影响区域和待求风机风轮盘面间重叠部分的面积;Ar是待求风机风轮盘面面积。已知风轮半径rr与尾流半径r以及2台风机间的展向距离y0,即可计算重叠面积Aoverlap与风轮盘面面积Ar。

在使用Jensen尾流模型优化风电场布局时需要考虑尾流影响面积的影响,将Jensen尾流模型的速度表达式代入式(9),则有

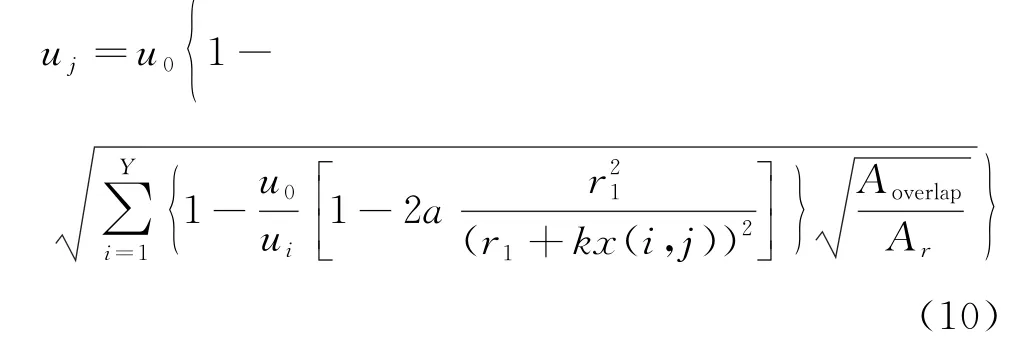
这里的ui与u0等价,均指引起尾流的风机轮毂高度处的风速,因此可以消去。基于Jensen尾流模型的多风机影响下尾流区域的风速可以表示为

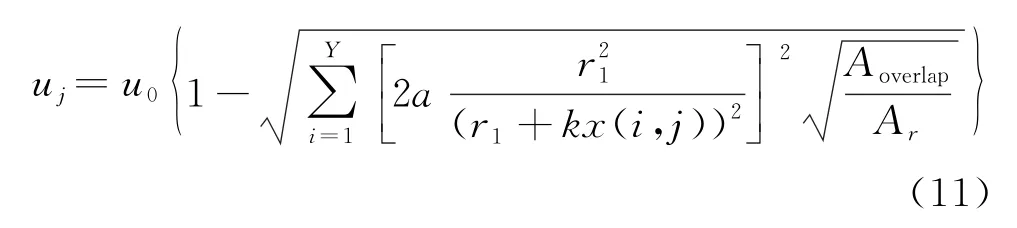
1.2 风速风向概率密度模型及风机模型

这里主要考虑了在风电场布局优化领域经常被提及的3种经典风速风向概率密度模型,该模型的设置主要是为了与领域内相关论文作对比。如图2所示,第1种风速风向概率密度模型是风以12 m/s的风速从同一个方向均匀流过风电场(单风向同风速入流),第2种风速风向概率密度模型是风以12 m/s的速度沿36个风向以相同概率流过风电场(多风向同风速入流),第3种风速风向概率密度模型是风以3种风速(8、12、17 m/s)沿36个风向以不同概率通过风电场(多风向不同风速入流)。风速风向示意图及第3种模型的风速风向概率分布图如图2—3所示。

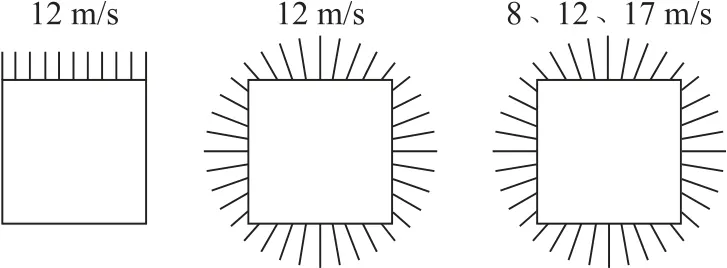
图2 3种经典风速风向概率密度模型示意图Fig.2 Schematic diagram of three classical probability density models of wind speed and direction

这里使用的风机模型是文献[10]中出现的风电场布局优化领域经典风机模型。风机叶轮半径20 m,轮毂高度60 m,推力系数0.88。

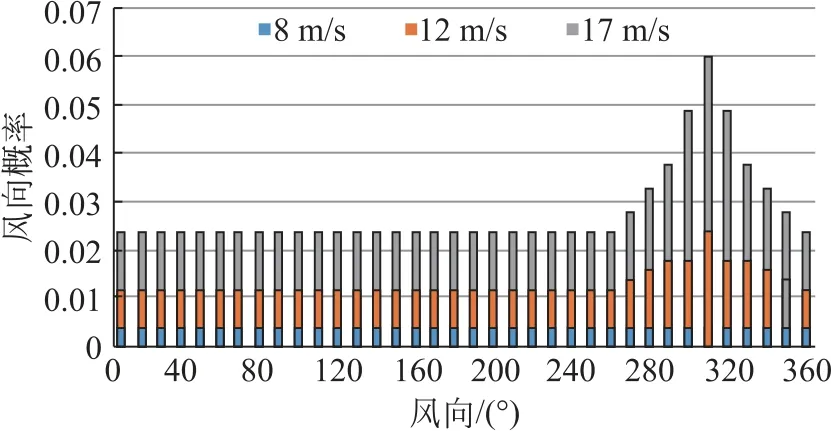
图3 第3种模型的风速风向概率密度分布图Fig.3 The probability density distribution diagram of wind speed and direction of the third model

根据文献[10],风机功率为

低于接入风速或高于切断风速时,实际风机功率为0 kW,文献中风机功率设定与这一情况不符。然而,为了与该领域的相关论文进行比较,这里仍然使用这个公式。

1.3 风电场布局优化问题的数学模型

设置的目标函数与Grady[11]使用的目标函数相同,定义为风电场的总发电功率除以风电场成本,即

式中:F为目标函数;Pmax为最大化的风电场发电总功率;C为风电场成本,其计算公式为

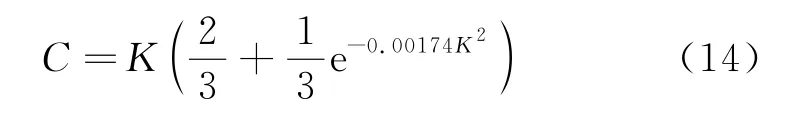
式中K为风机的个数。

2 风电场场内道路优化

场内道路优化算法[12]综合考虑A*算法、Dijkstra法、等高线树搜索法、prim 法、全局动态最小生成树算法,主要的目标是根据风机、已有路网,考虑县界、林地、生态红线、基本农田、建筑区域等各种限制因素,设置道路设计标准等参数,自动布置道路平、纵路线和横断面,最终可输出包含道路和平台的平、纵、横设计图纸,计算道路工程量。

2.1 风电场场内道路自动优化思路

算法主要是由2个部分组成,第1部分是如何得到地图上任意2点的道路,第2部分基于第1部分的结果,找到1个最短道路网将多个点联通起来。

同济大学的WANG Jun等采用等高线树搜索法+Prim 法得到符合坡度要求的道路网[13-14],如图4所示。河海大学采用的是Dijkstra+Prim 法。

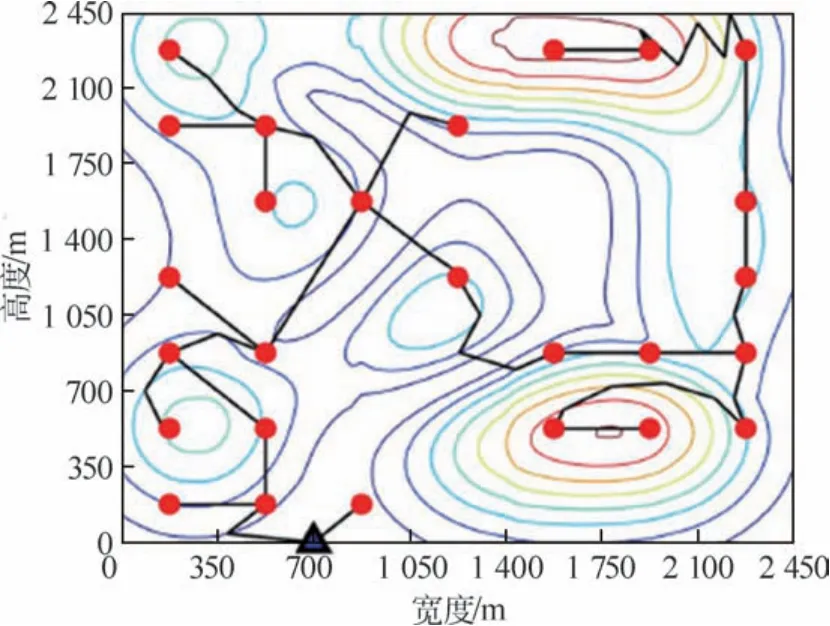
图4 风电场最优路径示例图Fig.4 Example diagram of optimal path for wind farms

上述2种思路在定线的过程中,改进了Dijkstra法。接着基于Prim 法做连通,解决线路性问题。但是Prim 法只处理节点的连通性,是无法得到实际工程中长出现的Y 型岔路。在这个前提下进一步改进了Prim 法,以获得更好的场内道路优化结果。

归纳总结整体的思路就是,采用Dijkstra法定线,再通过Prim 法得到连通性。通过改进了的Prim 法并不能达到设计院出图的水平,介于已经采用了Dijkstra+Prim+分支界限法,所以目前可以认为是非人工智能法的极限了。另外,在展线的过程中,确定了用退火的思想计算最佳纵坡线算法,算例如图4所示。

2.2 基于Dijkstra 方法的最短路径选择

Dijkstra法是经典的单源最短路径算法,是一个贪心法。当通过性不小于0时,此方法可以得到全局最优解。典型应用是用来得到网络节点之间的最小pin路径。现在将其改为路面坡度绝对值的分段函数。采用这样的函数可以使道路沿着等高线延伸,可避免出现设计场内道路是出现直接跨越山沟或者直接翻越山峰的情况。

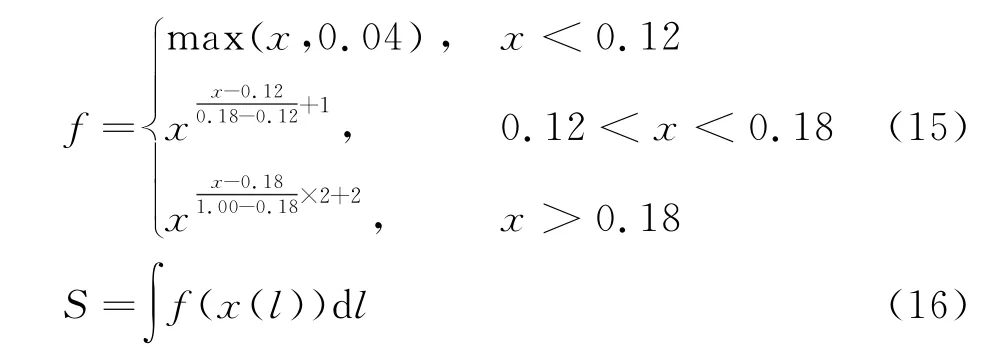
式中l为每段路径长度。

另外,为了能够让道路不出现急弯,在每一步更新下一步走向时,记录上2步的位置,当新分段路与旧路的夹角小于90°时,认为是不通的,这样就能避免结果出现急弯,如图5所示。

图5 风电场场内道路优化图Fig.5 Road optimization map in wind farm

2.3 基于Prim 原则的最短联通规划

原始的Prim 法是分成1个已联通点集和1个待联通点集,改进后是1个已联通边集和1个待联通点集,即每次搜索边到点的最短通路,这样就能得到Y 型岔路[16]。但这个方法是得不到十字岔路的,所以并非严格意义上的最优。

因本文提出的算法是在求解最小生成树的Prim 算法上做的改进,这里先引入一些Prim 算法的相关知识。Prim 法是个经典的最小生成树方法,同Dijkstra法一样也是个贪心法,该算法通过从根节点开始在每一步中选择待选边中边权最小的边来求得最小生成树。

风电场的场内道路优化问题可以看成求解最小生成树问题。即将风机看作图中的点,风机之间的电缆边长看作边权。Prim 算法和Kruskal算法常用于求解最小生成树,具有操作简单、求解效率较高等优点。

规划步骤如下:

(1) 定义Ayl、Bwl为 点 集,Cedge为边集。集合Ayl中保存已连接的点,在集合Bwl中装入需要连接的点(用符号Pi表示)。初始时,Ayl中装入点P1,即为{P1},点集Bwl中装入剩余点,即为{P2,P3,…,Pn},其中n为图中点的数量,此时Cedge为空集。待选边定义为以Ayl集合中各点为起点,集合Bwl中各点为终点的边。待选边的初始边权用W表示,定义为集合Ayl中各点到集合Bwl中各点距离乘以场内道路的造价。

(2) 初步计算从初始位置到Bwl中格点的权重,权重基于距离及坡度2个参数,权重与距离正相关,与坡度反相关。开始选定第1条边,从集合Ayl中的点P1出发,待选边有P1—P2、P1—P3、P1—P4直到P1—Pn,将选择边的终点装入集合Ayl,并将该点从集合Bwl去除,以此类推,重复该步骤,直到点集Bwl中无点为止。

(3) 根据电缆选型策略更新边权值,计算电缆总造价,输出该系数对应的最优电缆排布。即计算出电缆最短路径,然后依据距离及坡度参数的权重,乘以场内道路的造价。

2.4 递归二分插点生成纵坡初解

拉纵坡必须满足曲率半径和坡度要求,比较严格,若直接采用随机纵坡作为退火初解的话,满足约束要求的可能性很低。优化过程中参考并仿照实际生产工作中设计人员的设计过程,设计了递归插点的算法来得到初解。可归纳为如下几步:

(1) 先从自然纵坡起始到结束点拉1根直线,如图6(a)所示。即图6(a)中红色直线,此为道路纵坡优化第一阶段,确定起始结束点线段。

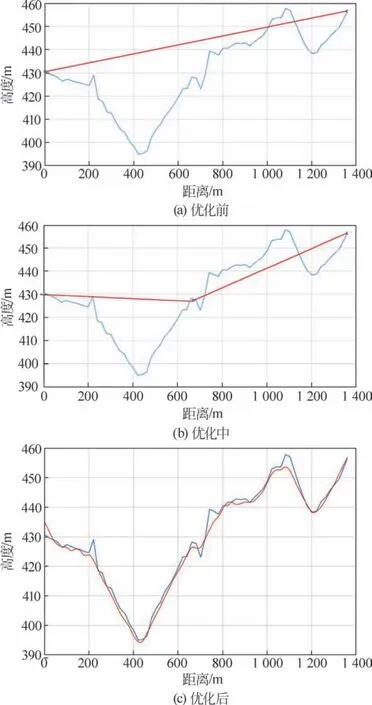
图6 风电场场内道路纵坡优化Fig.6 Longitudinal slope optimization of road in wind farm

(2) 然后从中找1个点,插入这个点能使红线和蓝线的面积差最小,当然还得满足其他约束条件的情况下才插(插入点不能离端点太近),如图6(b)所示。

(3) 重复步骤(2),在上一次插点得到的新的线段上不断插入新点,直到无点可插,如图6(c)所示。

2.5 基于退火算法的最小纵坡改造优化

基于退火算法的最小纵坡改造优化即采用退火原则,按照曲率半径、坡度限制、弯道展宽,最大挖深等约束,按照工程量或者造价或者其他什么指标最小原则改造自然纵坡。采用退火算法是因为本业务问题只有约束条件,没有先验原则,所以采用无方向性的随机寻优比较适合。

2.6 折线道路路径的圆化

实际生产工作中设计的道路是折线,在计算横断面之前,必须对折角做圆化,变成圆弧段的转弯,当有连续弯道时,就需要分别进行圆化,如图7所示。

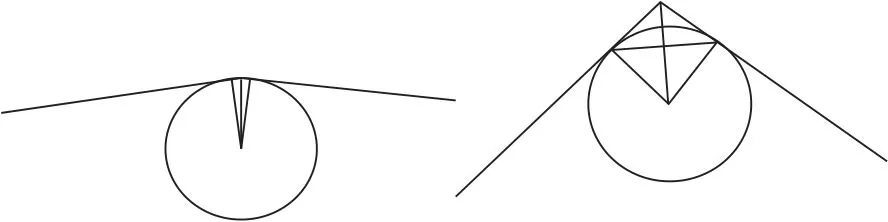
图7 风电场场内道路折线圆化示意Fig.7 The road in the wind farm is circular

本文采用的圆化原则是,用半径80 m 的圆来切折线,如果切点小于折线段的中点位置,则采用圆弧来代替折线,如果越过了中点位置,则按照中点的长度来计算1个最大切圆,将这个圆弧来代替折线,算例结果如图8所示。

图8 风电场场内道路折线圆化图Fig.8 Roundup diagram of road broken lines in wind farm

3 基于软件算法的风电场场内道路-机位排布自动优化方法实现

3.1 总设计流程

基于Jensen尾流模型,自动优化出风电机组机位排布结果后,采用本文提出的算法实现风电场场内道路自动优化。优化结果基于道路设计具体参数迭代计算,最终生成近似最优解,如图9所示。

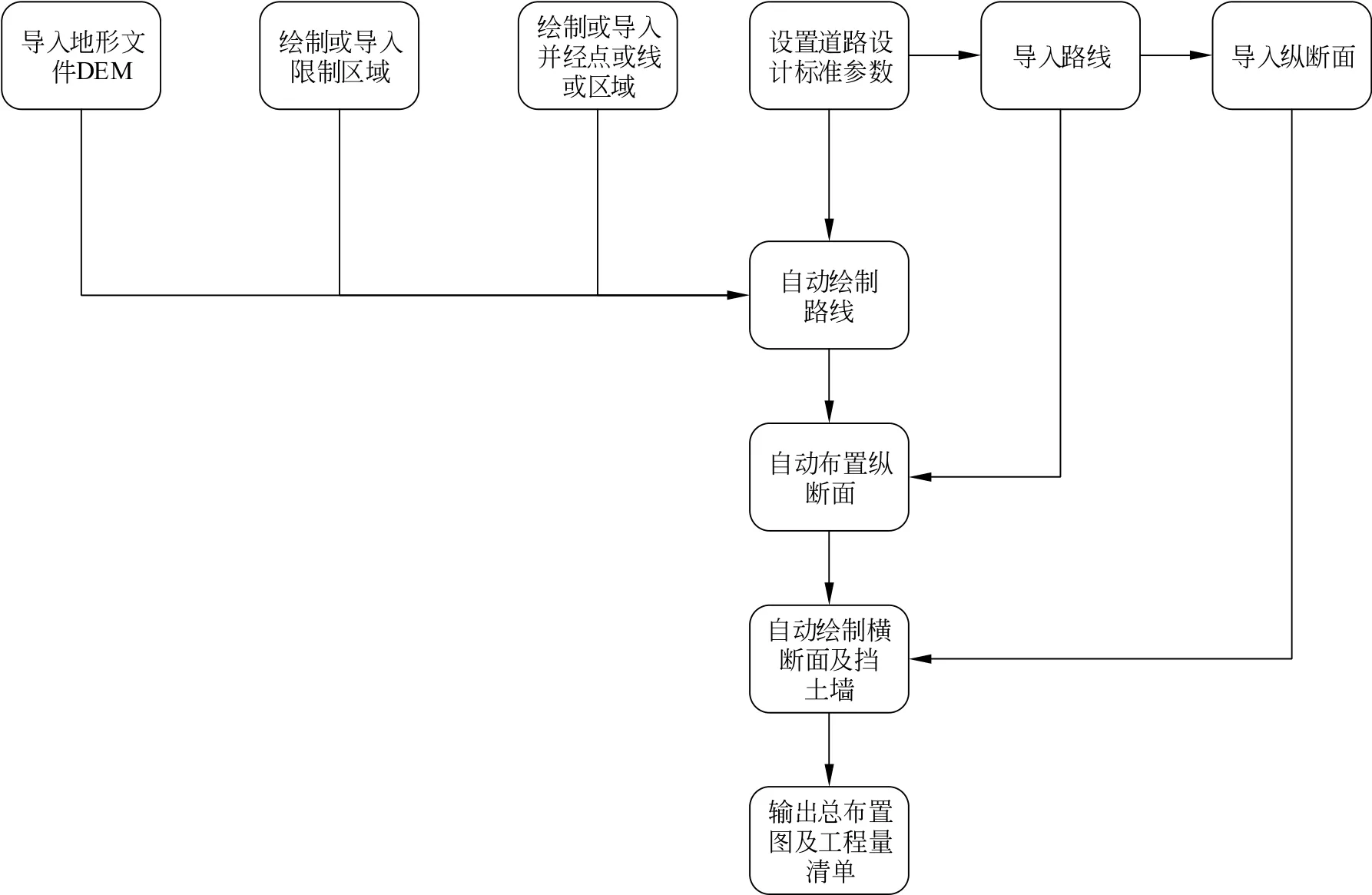
图9 风电场场内道路优化流程图Fig.9 Flow chart of road optimization in wind farm field

3.2 道路设计参数选择

(1) 道路横断面参数。

主要是选择道路等级,设置路基、路面宽度等横断面参数,作为后续横断面戴帽子设计的输入。并选择道路类别,得到路基宽度、车道宽度参数。

(2) 道路路线参数。

主要是选择运输方式,设置圆曲线最小半径、最小平曲线长度等平面参数,作为路线平面设计的输入。

(3) 路线纵断面参数。

设置最大纵坡、最小坡长等纵断面参数,作为路线自动拉坡设计的输入。

(4) 路基设计参数。

路基边坡及土石方参数主要是设置道路边坡坡率、坡高、边坡分级、马道宽度、是否设置碎落台等,作为后续横断面戴帽子设计输入。边坡坡率采用预设值设,默认为一级边坡,可自行修改预设值及边坡分级。输入路基土石比(如土方占40%,石方占60%),作为土石方工程量计算的设计输入,如图10所示。

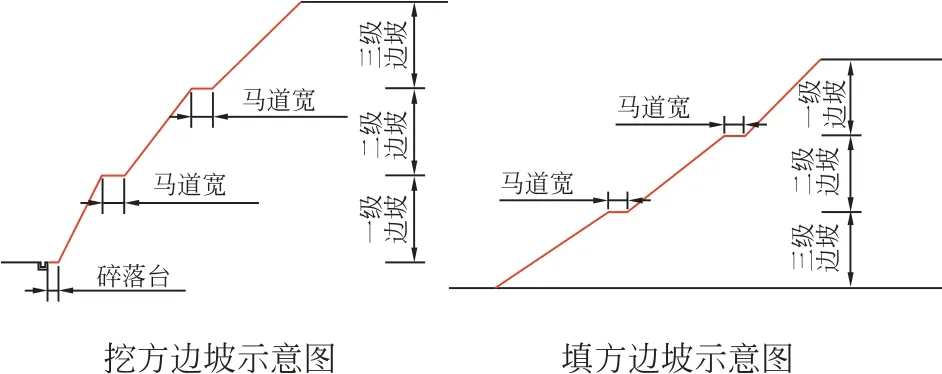
图10 风电场场内道路路基土方挖方填方示意图Fig.10 Schematic diagram of road subgrade earthwork excavation and filling in wind farm field

4 结论

本文基于Jensen尾流模型优化风机点位,并综合考虑Dijkstra法、等高线树搜索法、Prim 法等,使用全局动态最小生成树算法,并将Prim 算法进行了改进。原始的Prim 法是分成一个已联通点集和一个待联通点集,改进后,是一个已联通边集和一个待联通点集,即每次搜索边到点的最短通路,这样就能得到贴合实际工程效果的Y 型岔路,有效降低了场内道路的工程量和造价。