基于改进LMS 算法的谐波电流检测

李乾坤刘毅力刘圣荇

(西安工程大学电子信息学院,陕西省 西安市 710048)

0 引言

随着非线性负载和电力电子设备的大量使用,向电网输送了大量高次谐波电流,造成谐波污染,给电力系统带来不同程度的危害。而有源滤波器(active power filter,APF)作为抑制谐波效果较好的装置,可检测出谐波电流,并发出脉冲进行补偿,使流入电网的电流只存在负载电流的基波分量,达到抑制谐波的目的。

APF的性能与实时准确的谐波电流检测有关。经过不断发展,谐波电流检测的方法有多种。文献[1]中由于傅里叶变换检测方法计算量大,检测速度较慢,且存在栅极效应,提出了改进的滑窗离散傅里叶变换(discrete fourier transform,DFT)谐波电流检测法,降低了其计算量和使用空间。文献[2]介绍了自适应滤波电流检测算法,虽能对谐波电流进行检测,但其固定步长无法对收敛速度和稳态精度做到很好的平衡,于是对检测算法进行改进以提高检测精度。文献[3]中使用瞬时无功功率谐波电流检测时,由于低通滤波器平缓衰减性和动态调节能力不足,会导致谐波电流检测精度不高的问题,通过加入自适应滤波算法后检测的精度也得以提高。文献[4]在出现电压畸变及三相不对称的状态下,通过对比p-q法,ip-iq法,得出处于非理想条件下的ip-iq法能够较准确地检测出谐波电流,而p-q法在检测时则含有偏差。

本文在使用固定步长最小均方算法(least mean square,LMS)自适应的同时,为达到更好的效果嵌入低通滤波器进行自适应谐波电流检测,与主流的瞬时无功功率理论的谐波电流检测相比,该方法的优点是不依赖于电力系统参数,同时为了提高系统稳定性,算法将误差反馈信号与输入信号进行迭代,使均方误差达到最小,LMS 算法具有通用性[5],因此合适的迭代步长可以有效降低总谐波失真率。本文在选用合适的迭代步长时采用麻雀搜索算法(sparrow search algorithm,SSA)对参数进行优化,以取得滤波效果最好和总电流失真率最低的参数,并与固定步长LMS算法的经典参数及采用粒子群算法(particle swarm optimization,PSO)对其进行优化的结果进行比较。

1 自适应谐波检测算法

自适应噪声抵消技术的自适应谐波电流检测方法是由Widrow[6]提出,该方法更好地保持了系统的稳定性和适应性。目前最常用的是LMS 算法,其算法简单,易于实现。文献[7-8]将LMS算法引入到APF的谐波电流检测中,仿真结果验证了其可行性,LMS算法的检测系统是闭环结构,其优点是具有自适应性,适用于单相或三相系统,图1所示为自适应噪声抵消技术(active noise control,ANC)的原理图。

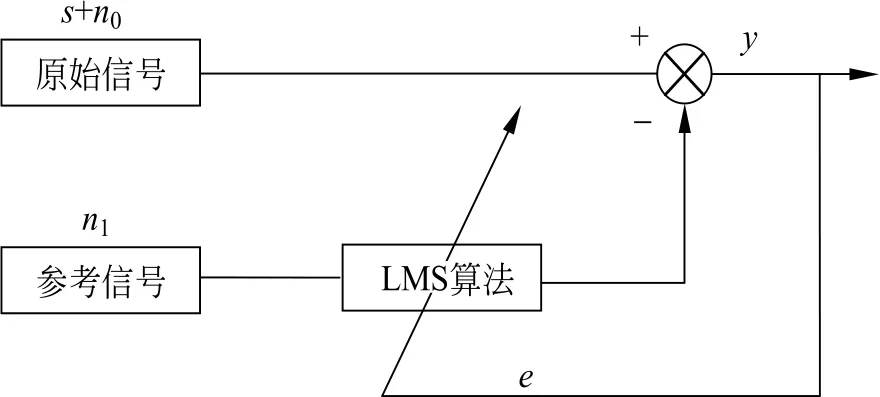
图1 自适应噪声抵消技术原理Fig.1 Principle of adaptive noise cancellation technology

s作为信号源,n0是干扰信号,s+n0是原始输入信号,n1是参考输入信号,n0和n1与s没有相关性,系统输出y是自适应LMS算法的最佳估计[9]。在谐波电流检测中,原始信号s+n0可当成非线性负载流过的电流iL(t),由基波和谐波电流构成。

2 有源滤波器和LMS 算法的结合

2.1 有源滤波器

本文在使用APF检测谐波电流时,采用自适应谐波电流检测算法,其原理是应用自适应干扰对消来进行信号的处理。检测系统会得到2个信号,即原始和参考信号,两者相互干扰,流经自适应滤波器后,实现互相抵消,并通过算法得到参考信号里的有效信号[10],以达到自适应有源电力滤波器参数的自我调节。因此,运用自适应算法通过误差反馈,调整步长因子,使滤波的权值做出相应改变,进而使结果更好地追踪基波电流,让APF产生补偿电流从而即时做出调整。

APF由检测电路、控制电路和脉冲宽度调制(pulse width modulation,PWM)逆变电路组成。APF的工作原理如图2所示。

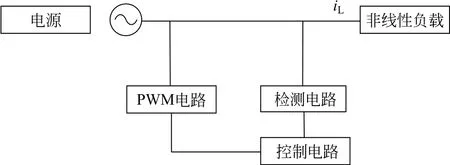
图2 有源滤波器的工作原理Fig.2 Working principle of active filter

APF通过检测出负载的谐波电流分量,然后控制逆变电路产生相应的补偿分量,使补偿分量等于谐波分量后,将补偿分量注入电网来抑制谐波电流分量。

电网电压为

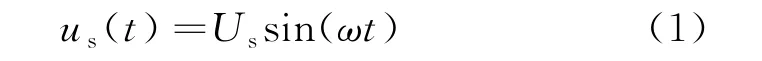
式中Us是us(t)的振幅。

iL(t)是非线性负载的电流,其波形是非正弦的,iL(t)可用傅里叶级数展开,即

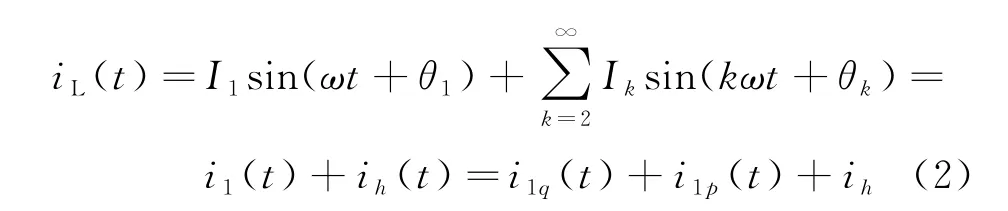
式中:i1(t)是基波电流;ih(t)是谐波电流的总和;i1q(t)和i1p(t)分别为基波电流的无功及有功分量。

2.2 谐波电流检测算法

基于ANC演变成的自适应LMS算法原理如图3所示,iL(n)是自适应谐波电流检测中的期望信号,输入信号x(n)是电压锁相环(phase locked loop,PLL)的信号,x1(n)和x2(n)是电压的正弦信号和余弦信号。滤波器系数向量的相应权重为w(n),输出y(n)是通过权向量w(n)不断迭代得到的新的近似期望信号,e(n)是当前谐波信号[11]。

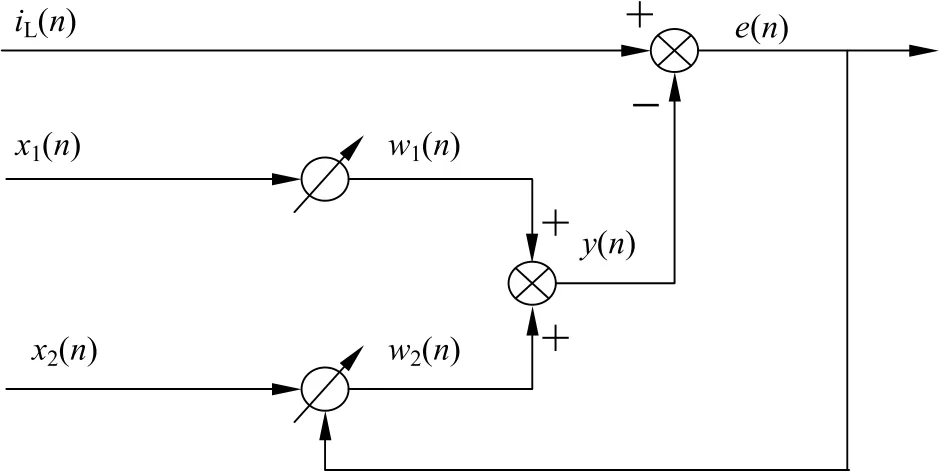
图3 谐波电流检测自适应LMS算法原理Fig.3 Principle of adaptive LMS algorithm for harmonic current detection

LMS算法的更新迭代公式为

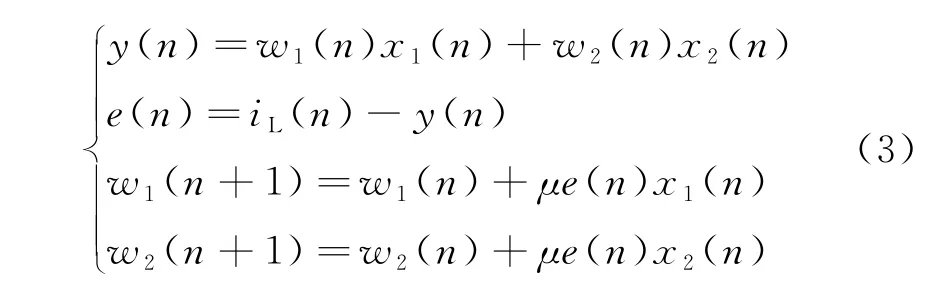
谐波信号e(n)也叫误差信号,根据e(n)不断调整滤波器的权值w1和w2,使y(n)追踪iL(n)的变化,不断接近iL(n)的幅度和相位,从iL(n)中减去y(n)便可得到谐波信号。但是需要证明iL(t)、sinωt和ih（t）三者能达到自适应滤波的条件[12],可以使用Matlab中的corrcoef语句来验证它们之间的相关性,结果表明iL（t）和sinωt是相关的,sinωt和ih（t）不相关,iL（t）和ih（t）也不相关,因此自适应滤波器适合谐波检测。

LMS算法的本质是利用瞬时值估计梯度矢量[13],其的权值更新为

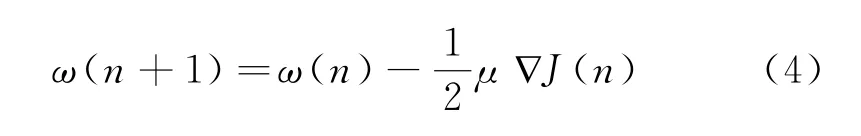
式中:μ为最小均方算法中的迭代步长;∇J（n）表示瞬时梯度,LMS的均方误差为J（n）=|e（n）|2。

则∇J（n）可作相应变换

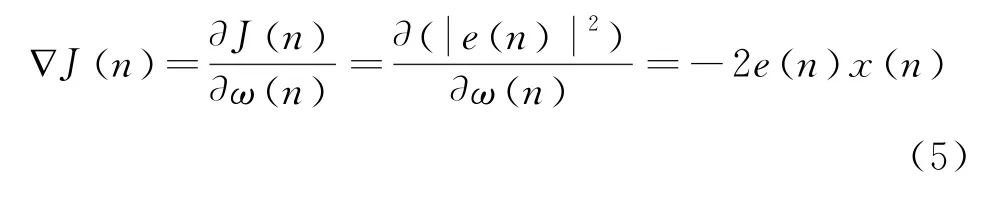
将式(4)(5)进行合并整理,可得

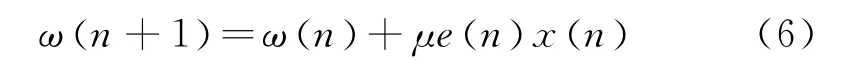
同时,算法还要满足

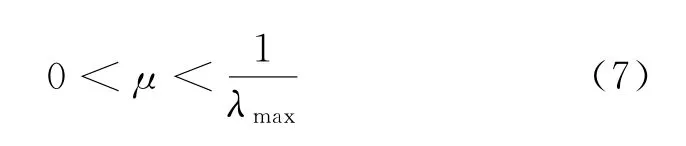
式中λmax为输入信号自相关矩阵R=E[x(n)xH(n)]的最大特征值。

综上,便会得到输入信号y（n）和误差信号e(n),即

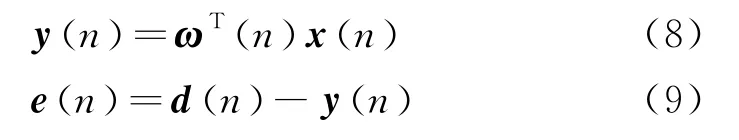
同时,收敛时间τmax和稳态误差M和迭代步长μ三者间的关系为

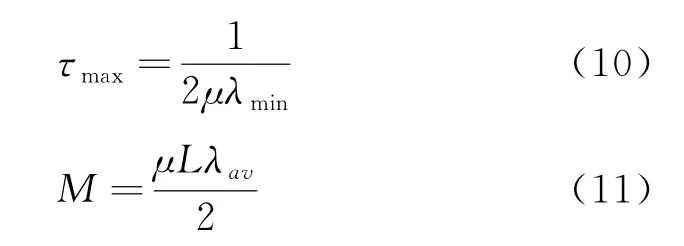
式中L为自适应滤波器的长度[14]。

由式(10)(11)可知,迭代步长μ会影响算法τmax的快慢及M的大小,步长与τmax成反比,与M成正比,当选择的μ值较大时,τmax值很小收敛速度快,但稳态精度M差。而当μ逐渐减小时,τmax收敛速度变慢,其稳态精度M不断提升。因此,在进行最小均方固定步长算法的研究与应用时,迭代步长的选择尤为关键,选择合适的步长因子μ,可使权重得到优化,从而得到更精确的谐波电流。本文采用SSA 算法来优化固定步长的参数值,并与经典的步长参数及PSO 算法进行比较,以证明选用SSA算法的合理性、优越性。

2.3 嵌入低通滤波器

本文在模型中嵌入了无源RL 低通滤波器,由于只允许通过低频信号,阻止高频信号,因此可使部分高次谐波信号得以滤除,本文的研究重点是分析自适应滤波对非线性负载流经电网产生谐波的抑制效果,为了方便控制变量来探求滤波效果的好坏,低通滤波器没有选择使用FIR 滤波器或IIR 滤波器[15-18]。

在控制方法上,本文使用滞环控制方式,将流入电网的电流信号Is与SSA 算法得到的基波电流信号Iref进行比较,通过滞环控制模块,设置产生触发脉冲的时间在0.08 s,向APF 发送脉冲信号,进而控制补偿电流的大小,抵消谐波电流。

3 基于SSA 算法的自适应滤波器的参数优化

3.1 目标函数

采用SSA 算法对自适应滤波器中的参数进行优化,所需优化的参数为a、b、c三相迭代步长μ1、μ2和μ3,种群中麻雀的位置信息代表各个参数。本次优化是希望补偿非线性负载产生的全部谐波分量,并使注入电网的电流只存在负载基波有功及无功电流,因此要使APF通过LMS算法得出的基波电流与流入电网的电流差值尽可能地小,从而达到抑制谐波的目的,目标函数为

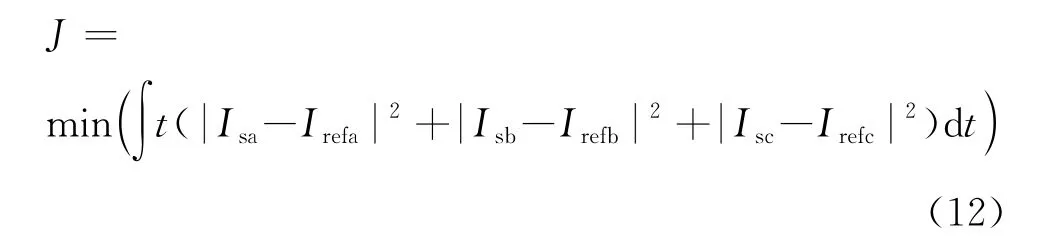
式中:Isa、Isb、Isc是流入电网的三相电流;Irefa、Irefb、Irefc是通过算法得到的三相基波电流。约束条件μ1、μ2、μ3的取值范围为[0.0001,0.1]。

3.2 优化算法比较

为验证SSA 算法在参数优化上的优越性,选用经典固定迭代步长,SSA 和PSO 算法这3种方法进行对比,并取a、b、c三相迭代步长的仿真结果进行分析。

SSA 和PSO 算法的相同参数为:种群数量为50,迭代次数为100,参数μ1、μ2 和μ3 的范围和目标函数如上所述。SSA 算法的预警值取0.8,发现者比例为0.2,警戒者比例为0.1。PSO 算法的惯性因子ω=0.6,加速常数c1和c2都取2。

表1是固定迭代步长和经SSA 及PSO 算法得到的a、b、c三相步长μ1、μ2、μ3,SSA 和PSO 相应的参数优化曲线、最优适应度值曲线及仿真模型的电压电流波形分别如图4—5所示。

表1 迭代步长的优化参数Table 1 Optimization parameters for iteration step size

图4(b)中,为了更好地观察3个参数的变化,将PSO 参数中的μ2、μ3 的值放大了100倍。通过对比发现SSA 和PSO 的收敛迭代次数分别是34次和26 次,这说明SSA 优化曲线的下降速度较PSO 而言不相上下,都能够快速地找到最优解。而最优适应度值分别是2.967和6.498,适应度值越小,说明所能达到的最优值最好,这表明SSA 在参数寻优能力方面较PSO 更强。

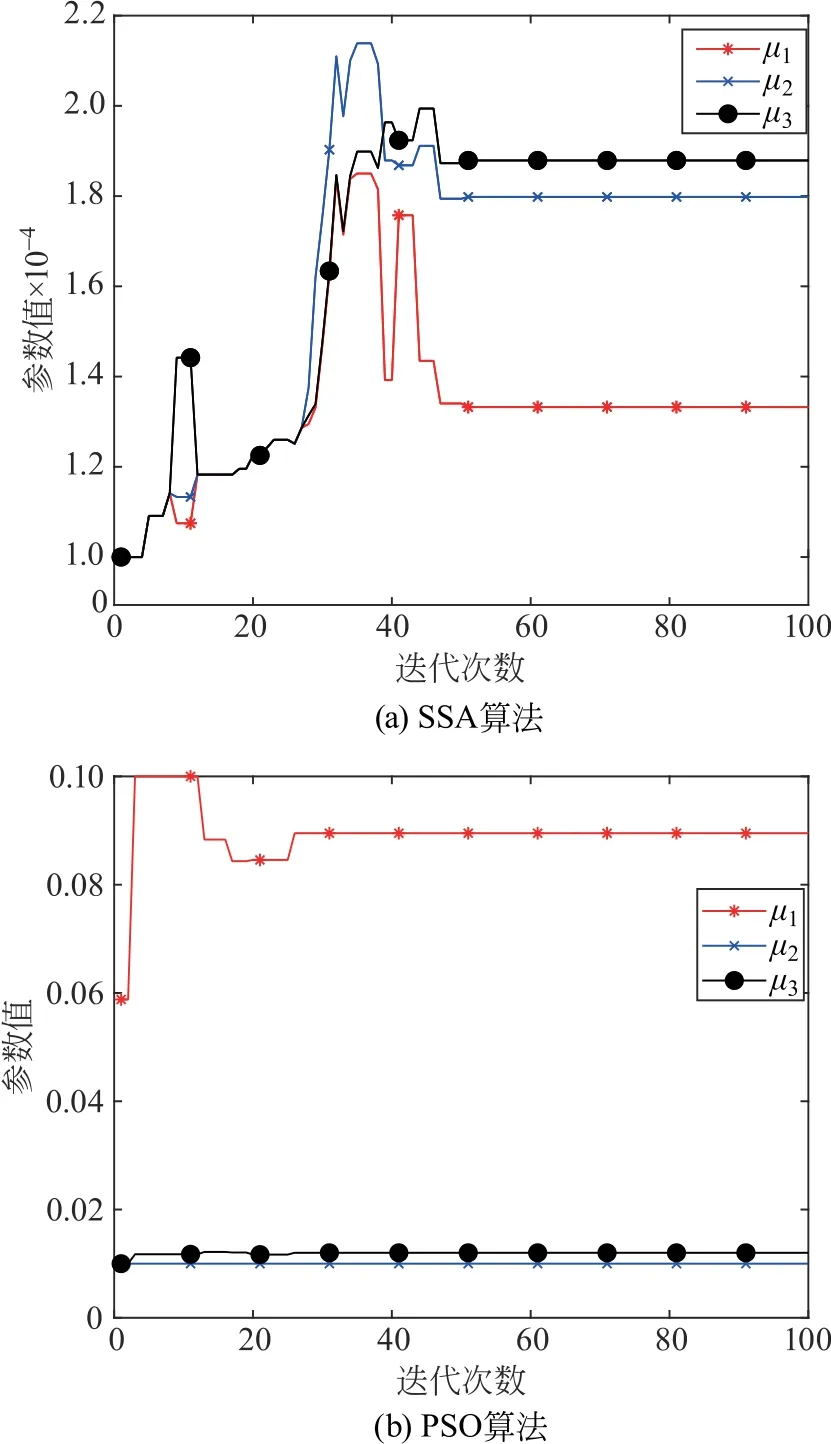
图4 SSA算法和PSO 算法的参数优化曲线Fig.4 Parameter optimization curves of SSA algorithm and PSO algorithm

有源电力滤波器中采用固定步长LMS进行谐波电流检测的仿真结果如图6所示,其中一、三、四波形中的红绿蓝三种颜色分别代表a、b、c三相的电流波形。

使用麻雀搜索算法,粒子群算法对滤波器参数进行优化时,其仿真的波形结果如图7—8所示。

图7中第1个波形为未经过APF 时负载的电流IL波形,虽然经过了低通滤波器,但还能明显看出负载的电流有谐波分量并产生了畸变,第2个波形为APF用来产生补偿谐波的电流If,谐波与其进行抵消后使电路中只存在基波电流,由于采用了不同的3种方法,可以看出产生补偿谐波的电流波形也不近相同,第3个波形是APF经3种算法检测得到的三相基波电流Iref,第4个波形是经APF 滤波后最终流入电网的三相电流波形Is。

将固定步长LMS算法进行谐波补偿的结果与上述2种方法得到的结果进行对比分析可知,使用麻雀搜索算法优化参数后最终流入电网的电流Is波形效果最好,电流中产生的谐波含量已基本滤除且为正弦波,补偿的谐波电流更符合要求,而采用PSO 算法的效果最差。因此可使用麻雀搜索算法来对自适应滤波的参数进行优化,以达到滤除谐波的效果。

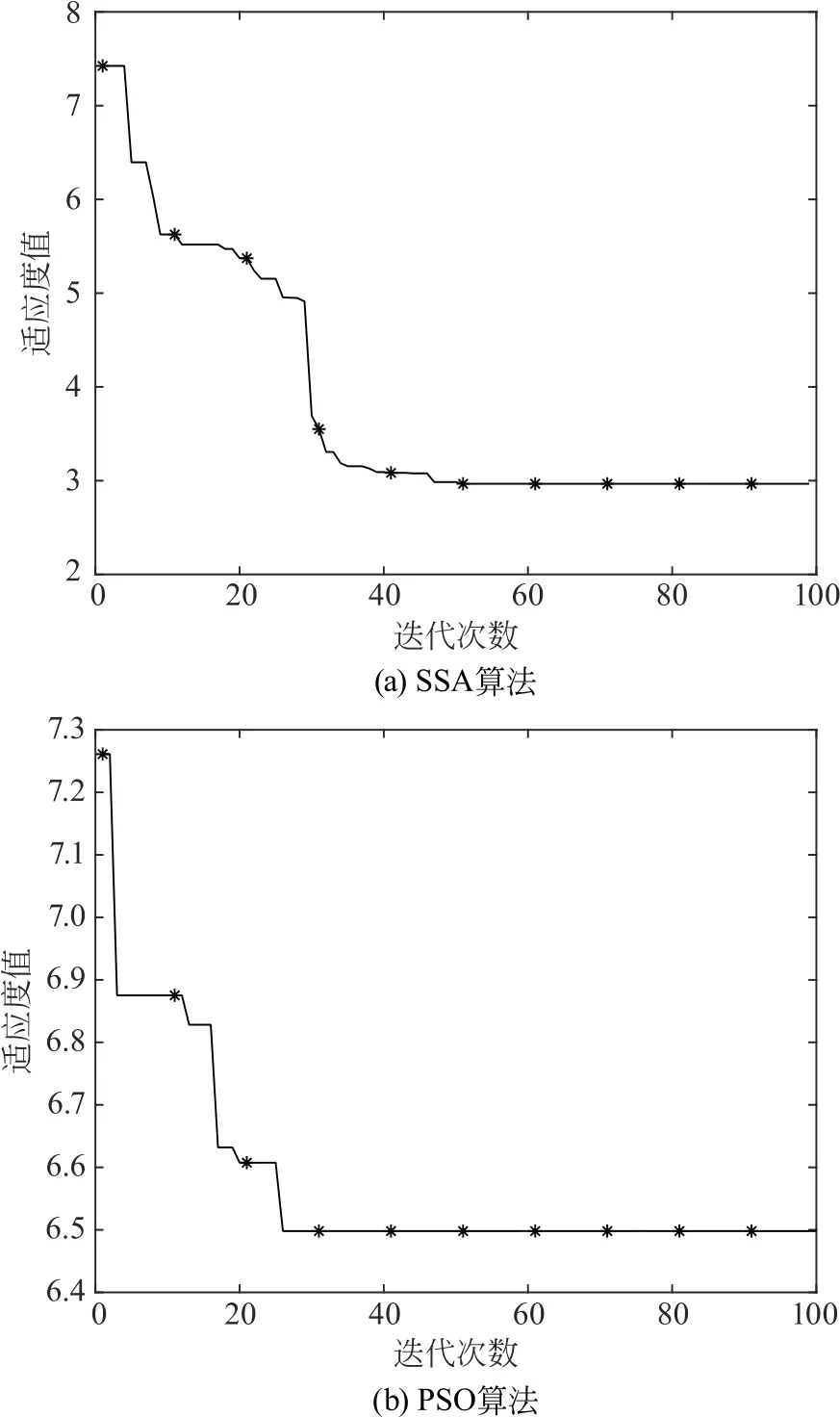
图5 SSA算法和PSO 算法的最优适应度值Fig.5 Optimal fitness values of SSA algorithm and PSO algorithm

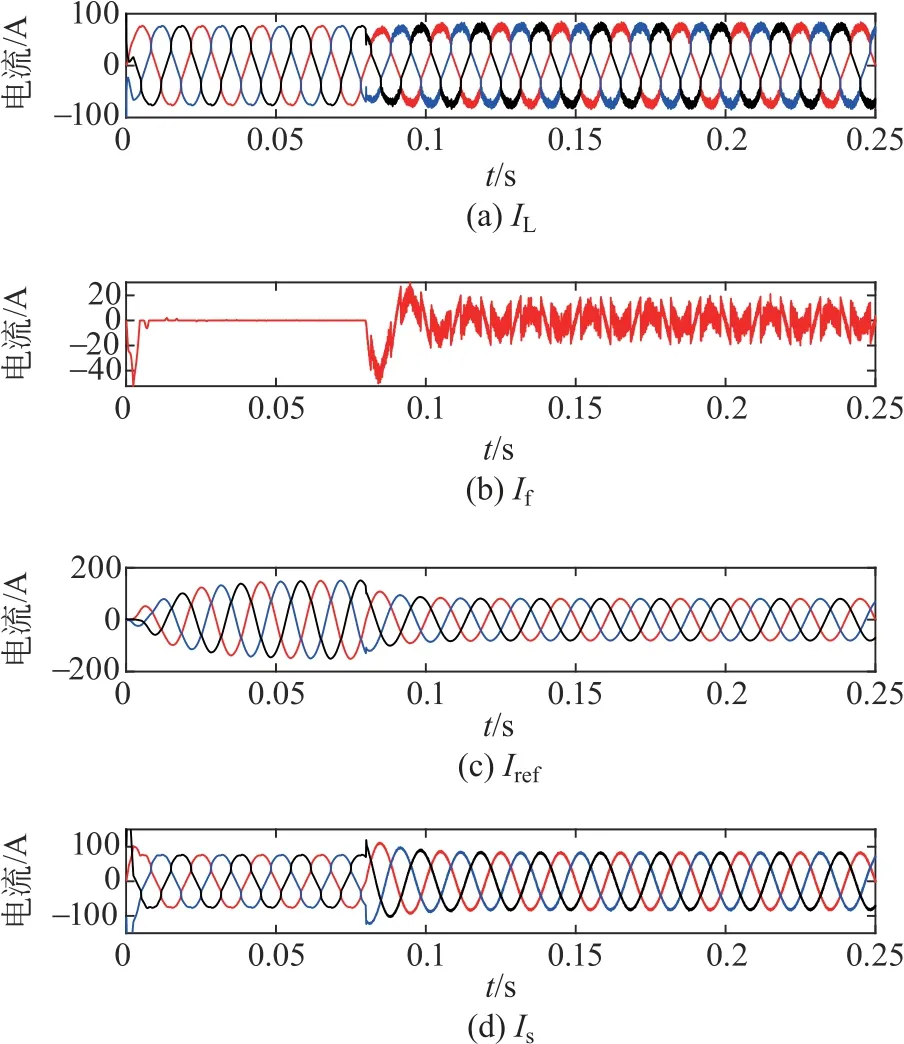
图6 固定步长的仿真波形Fig.6 Simulation waveform with fixed step size

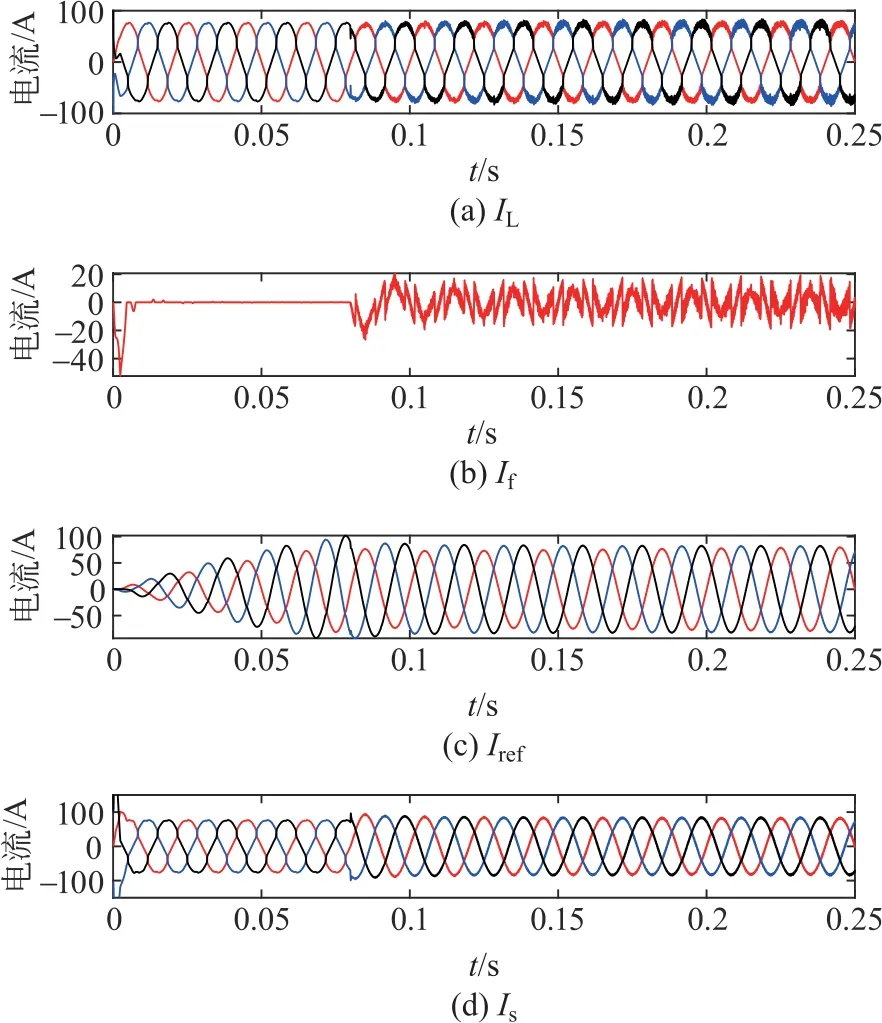
图7 SSA算法确定a、b、c三相步长的仿真波形Fig.7 Simulation waveforms of a,b and c three-phase step sizes determined by SSA algorithm

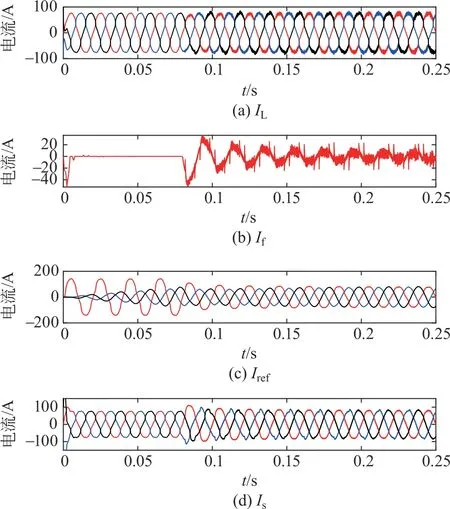
图8 PSO 算法确定a、b、c三相步长的仿真波形Fig.8 Simulation waveforms of a,b and c three-phase step sizes determined by PSO algorithm

4 总谐波畸变率分析

本文在仿真模型运行中,为进一步验证滤波的效果,在模型中进行了总谐波畸变率分析。图9是固定步长取典型参数0.001、PSO优化参数和SSA优化参数下的总谐波畸变率仿真分析结果。由图9可知:采用固定步长LMS算法检测嵌入低通滤波器时的谐波总失真率为6.46%,未能降低到5%以下,不满足IEEE标准,这表明当系统中固定步长参数未选择合适的值时,滤除谐波的效果不好,流入电网中的电流还存在一定量的谐波,而在SSA 策略下谐波总失真率下降到3.35%,PSO 策略下谐波总失真率的值为7.83%,三者补偿后的三相电力系统几乎都为正弦波,但SSA 算法优化参数后的结果对降低线路谐波的效果更显著,但使谐波总失真率降低到5%以下,满足了IEEE 标准,这表明了使用该算法的实用性,因此可使用SSA 算法对参数进行优化以达到滤除谐波最好的效果。

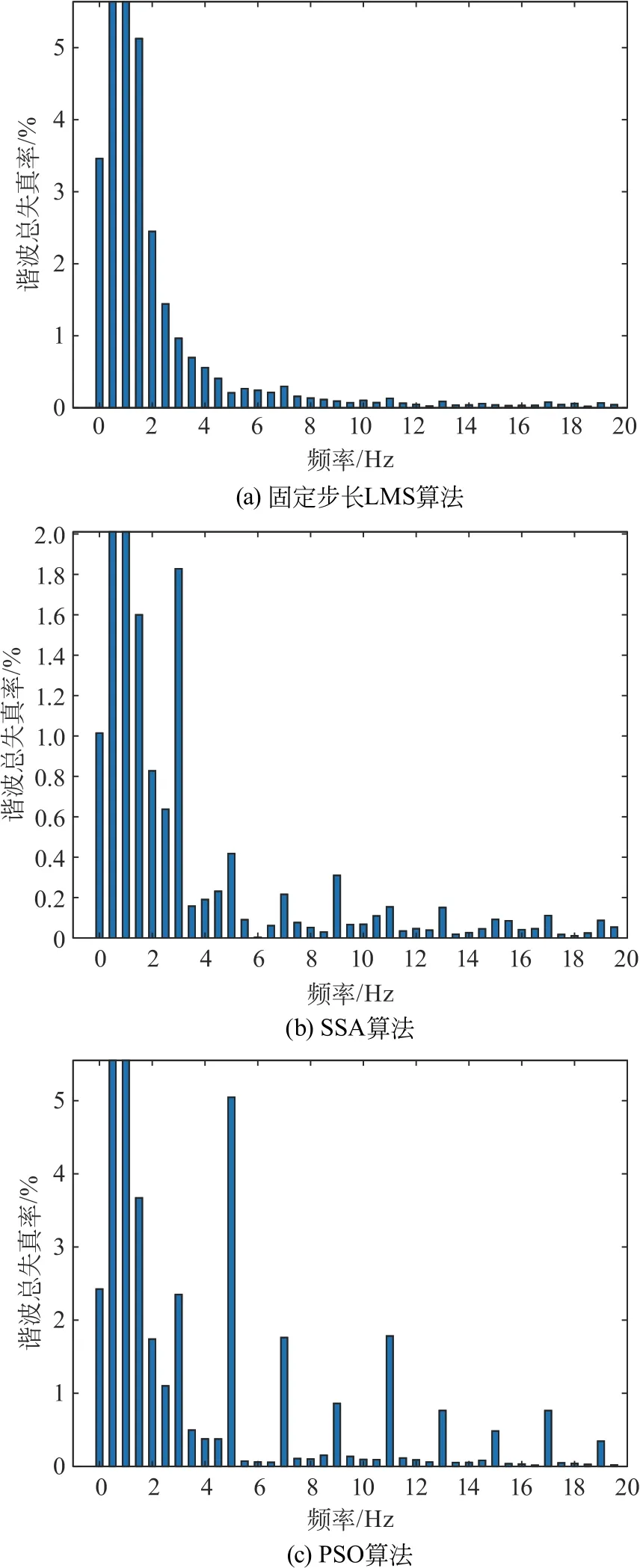
图9 3种算法优化参数后谐波总畸变率分析Fig.9 Analysis of total harmonic distortion rate after optimizing parameters by the three algorithms

本文在验证使用SSA 算法优化参数的适用性时,选取了2组不同的负载参数进行对比,在进行仿真分析时,负载参数的选择如表2所示。

表2 负载参数取值Table 2 Load parameter values

本文在3.1节采用SSA 算法优化参数进行仿真分析时,其负载参数为表2中的参数一,仿真波形如图7、9(b)所示。选用负载参数二的仿真波形如图10—11所示。

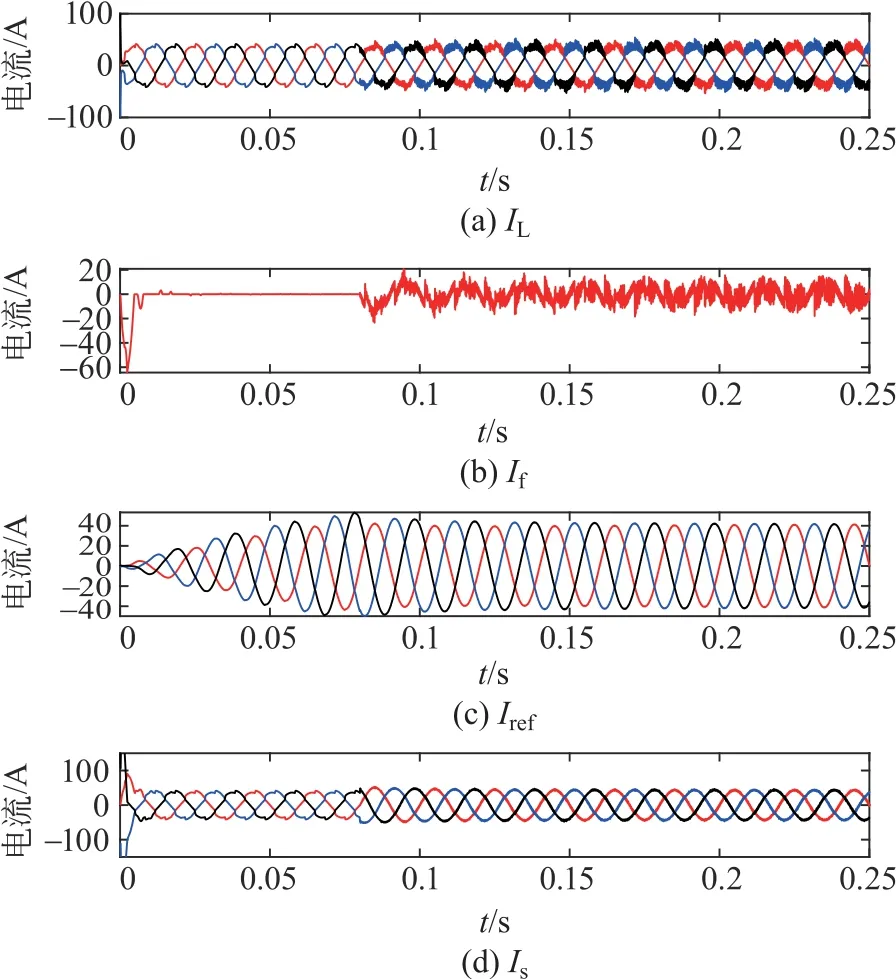
图10 采用SSA算法确定a、b、c三相步长的仿真波形Fig.10 Simulation waveforms of a,b and c three-phase step sizes determined by SSA algorithm

对比2种参数的仿真结果可以分析得出,不同的负载在使用SSA算法优化步长参数后,经APF同样可以很好的达到抑制谐波的效果,使流经电网的电流达到几乎只有基波电流的水平,如图10流入电网电流的波形,总谐波畸变率都为4.88%,均降低到5%以下,满足了IEEE 标准,表明了使用不同的负载,并不会影响麻雀搜索算法优化参数后的抑制谐波效果。

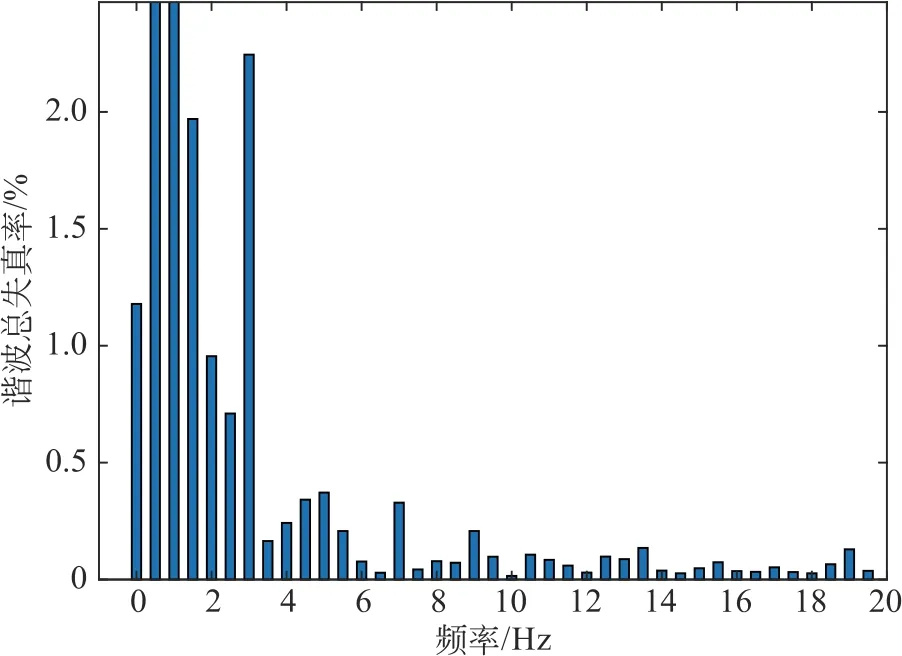
图11 SSA算法优化参数后谐波总畸变率分析Fig.11 Analysis of total harmonic distortion rate after optimizing parameters by SSAalgorithm

5 结论

本文使用SSA 算法对自适应滤波中的滤波参数进行优化,步长参数的好坏直接影响到滤除谐波的效果,同时对比了选用经典步长参数,PSO 算法优化参数后的效果,从三者最终流入电网的电流波形以及总谐波畸变率的仿真结果可以看出,选用SSA 算法,滤除谐波后的波形效果最好,谐波畸变率最低,并且在选用不同负载参数时,仿真的波形表明此方法同样适用于不同负载参数的情况,验证了该方法的有效性和可行性以及适用性。