基于电流拍频特性的单相自适应重合闸故障识别方法

贺雨昕张 颖常新建吴 成

(西安工程大学电子信息学院,陕西省 西安市 710048)

0 引言

高压输电线路上发生的故障中以单相接地故障为主,并且多数单相接地故障表现为瞬时性,所以采用自动重合闸技术可大大提高电力系统供电可靠和稳定性[1-4]。但自动重合闸存在非常明显的缺陷,即一旦重合于永久性故障,则会给电力系统带来严重的影响,对电力设备带来二次伤害[5],甚至发生大规模停电事故,因此,为避免这种情况发生,相关学者又提出了自适应重合闸的概念[6]。自适应重合闸在重合前对于故障性质做出判别,当故障性质为瞬时性时,发出合闸命令进行合闸操作,否则,不允许进行合闸操作,因此可有效避免重合于永久性故障带来的损害。

目前单相自适应重合闸技术已经得到了广泛的研究与应用[7-10],其主要研究方法根据故障后的不同阶段分为2类:(1)基于断开相恢复电压阶段。文献[11]理论分析了恢复电压的组成,提出了采用恢复电压拍频特性作为无故障判据。除此之外,还将改进型相关法[12]、Prony法[13]、人工智能[14]等数学处理方法应用于故障性质判别。但恢复电压不到线路额定电压的10%,测量精度难以保证,导致利用恢复电压的判据结果可靠性存在较大问题。(2)基于故障电弧阶段。文献[15]将小波变换应用于重合闸中,主要是利用其检测电压的极大值来识别故障性质。文献[16]基于模电流双窗函数的暂态能量比提出了一种新判据,利用所设计的窗函数提取高频信号前、后时段的能量,通过能量比构成判据。因电弧过程复杂,利用故障电弧构建准确模型困难,因此普遍采用恢复电压阶段的电气量来构建判据。

本文提出一种基于断开相并联电抗器电流拍频特性的单相自适应重合闸故障性质识别方法。针对瞬时性故障断开相并联电抗器电流的拍频特性,利用正弦波预测算法构造符合正弦特性的预测波形,与实际波形进行对比,提出利用波形互相关系数来进行故障性质识别的方法。该法原理浅易,计算简便,通过Pscad/Emtdc对各种故障情况进行大量验证,结果证明了该判据的可行性与适用性。

1 故障相并联电抗器特征

1.1 瞬时性故障

以线路发生A 相瞬时性单相接地故障为例进行分析,如图1所示。

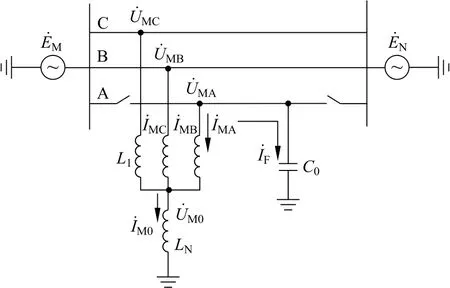
图1 瞬时性单相接地故障等效电路图Fig.1 Transient single-phase ground fault equivalent circuit diagram

线路发生单相接地故障后,故障相断路器跳闸,电弧熄灭,瞬时性故障的故障点消失后,由健全相线路继续运行。由于并联电抗器的存在使得线路中储能元件存储的能量在电感电容之间充放电,从而产生低频自振分量。因此,断开相并联电抗器的电流由工频分量和低频自振分量2部分组成。

由图1等效电路图可得

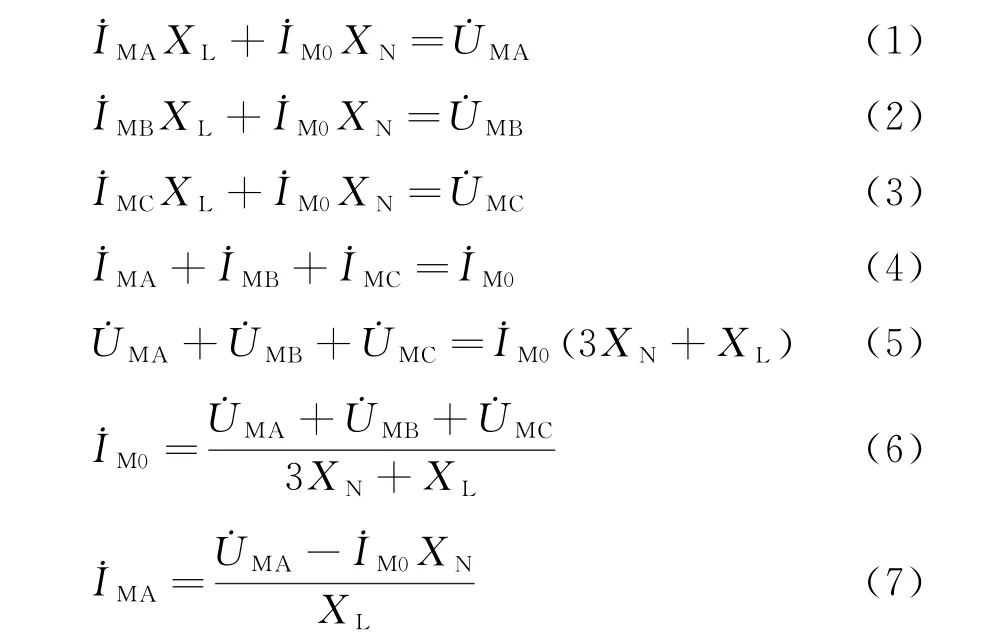
式中:XL=jωL1;XN=jωLN。

恢复电压阶段,断开相并联电抗器电流由工频分量与低频自振分量组成,其瞬时表达式可表示为

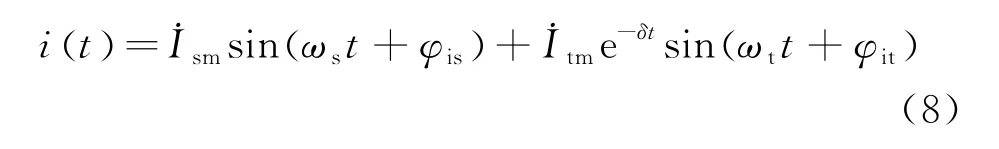
1.2 永久性故障

输电线路发生永久性故障时,线路的储能元件存储的能量由于故障点一直存在,会持续对地放电。

(2) 当经过渡电阻发生接地故障时,断开相并联电抗器电流为

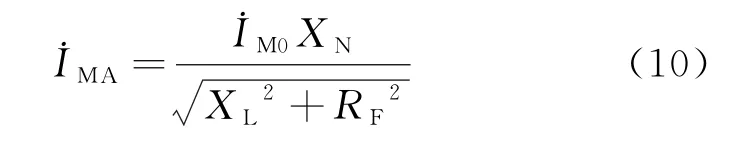
可见,当过渡电阻RF增大时的值会随之减少。

永久性故障下的故障相并联电抗器电流主要由工频分量组成,表示如下:

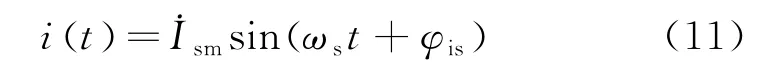
通过分析可知,在不同的故障性质下,断开相故障回路差异明显,断开相并联电抗器电流呈现出不同的组成,因此,本文提出一种基于断开相并联电抗器电流特性来进行断路器单相重合前故障性质判别的方法。

2 基本原理及判据

利用瞬时或永久故障断路器跳闸后的二次电弧阶段符合正弦特征的短数据窗来构造一个符合正弦特征的预测波形,然后将采样得到的实际电流波形和构造的预测波形进行相关性分析,通过2个信号的归一化互相关系数计算,来对线路故障的不同性质进行识别。

2.1 正弦波预测算法

结合文献[17]的正弦波预测算法对断开相并联电抗器电流进行预测。

(1) 设原始信号x(n)为采样得到的断开相并联电抗器电流,原始信号在二次电弧阶段存在直流衰减分量,会对后续预测产生干扰,因此首先对其进行低通滤波处理:

(2) 设置预测波形起点,并采用最大面积法确定最佳计算起点:

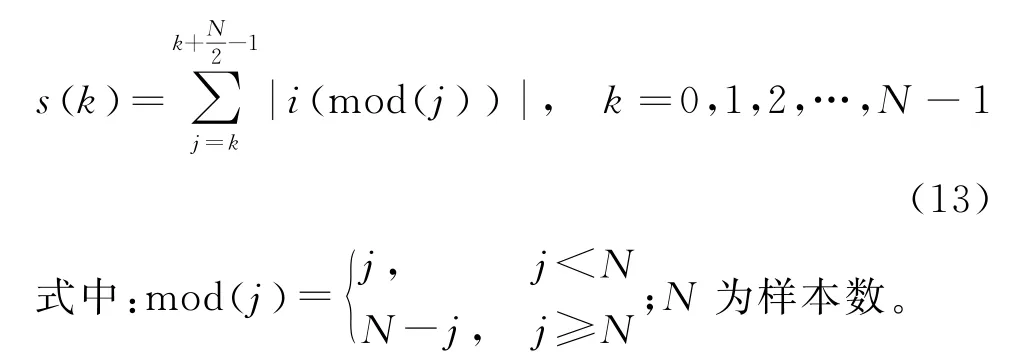
计算N个s（k）,然后取s（k）的最大值所对应的k值作为x(n)的新起点。

(3) 判断x(n)上的点是否满足正弦特征。正弦信号上相邻的3个采样点应满足

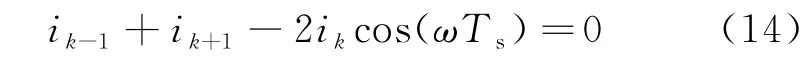
式中Ts为取样周期。从x(n)的预测起点处取3个相邻的采样点,利用式(14)对其进行判断,若满足,则由这3点进行波形预测。

(4) 利用算法得到预测信号y(n)。式(14)可写为

通过上述步骤即可得到断开相并联电抗器电流在瞬时性和永久性故障下的预测正弦波形。

2.2 互相关系数

由前述分析可知,瞬时性故障恢复电压阶段电流实际采样波形存在拍频特性,因此与预测正弦波形差异较大,而永久性故障时2 种波形保持一致。通过上述算法对采样波形进行处理,并得到预测波形后,对2种波形的互相关系数进行计算,来判断2种信号的相似程度,本文采用归一化互相关系数[10],可以排除信号幅度的影响。

3 瞬时性故障判据及实现方案

3.1 瞬时性故障判据

为反映输电线路在不同故障性质下电流波形的互相关程度,便于对瞬时性故障进行识别,利用2种不同故障下电流波形信号互相关系数的特点,在计算两种波形互相关系数的基础上提出如下判据:

(1) 判据1为

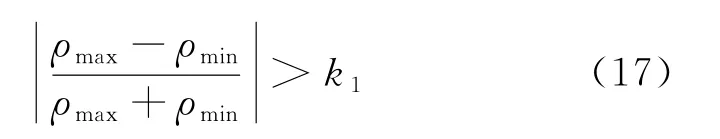
(2) 判据2为

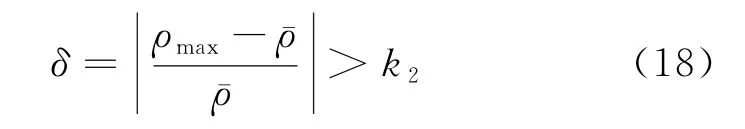
式中:ρmax为在一个计算周期内断开相并联电抗器电流预测波形与实际波形互相关系数的最大值;ρmin为1个计算周期内二者互相相关数的最小值;ˉρ为1个计算周期内二者互相关系数的平均值;k1、k2为整定值,考虑到误差,k1一般取0.5,k2一般取0.05。

3.2 单相自适应重合闸方案

根据上述瞬时性故障判据,提出重合闸方案,方案流程如图2所示。

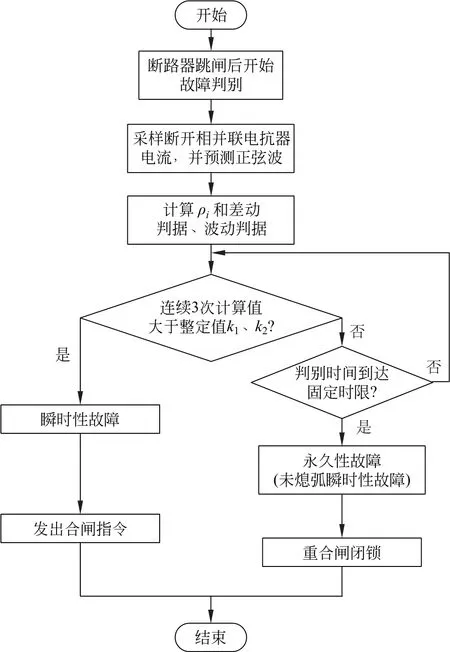
图2 单相自适应重合闸流程图Fig.2 Flow chart of single-phase adaptive reclosing

(1) 以A相线路发生单相接地故障的情况为例,在发生故障相断路器跳闸之后,采集A 相的断开相并联电抗器电流数据,得到其离散数据序列。

(2) 将断开相并联电抗器电流的部分离散数据序列带入到式(15)中,得到1个正弦波的离散数据;然后将正弦波的离散数据序列和采集电流的离散数据序列带入到式(16)中,求出2个信号的互相关系数ρ,数据窗为20 ms;再将ρ带入到故障判据1和2中,求出计算结果,数据窗为115 ms。

(3) 当故障判据的计算结果连续3次大于整定值时,判定为瞬时性故障已熄弧,可进行合闸操作,即发出合闸命令;当故障判据的计算结果小于整定值时,判定为永久性故障,不可进行合闸操作,即发出闭锁重合闸的命令。

4 仿真验证及分析

4.1 系统仿真模型

为了对本文提出的瞬时性故障判据进行准确性和可靠性验证,采用Pscad/Emtdc搭建图3所示双端带并联电抗器的500 k V 线路模型,进行仿真验证。输电线路的具体参数如表1所示。

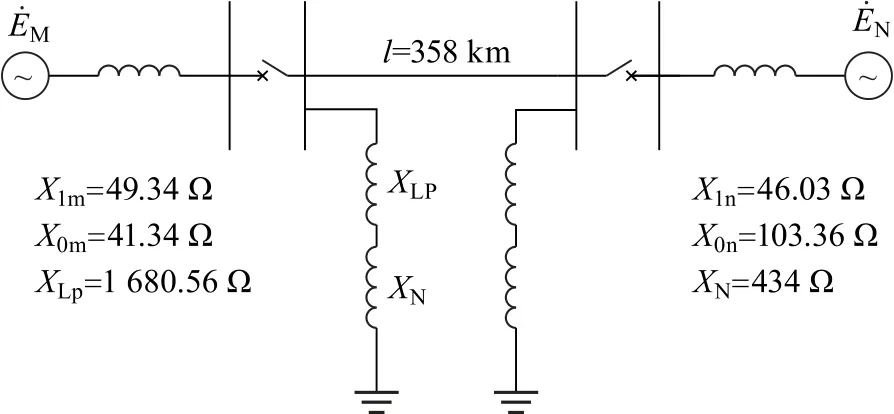
图3 输电线路仿真模型Fig.3 Transmission line simulation model

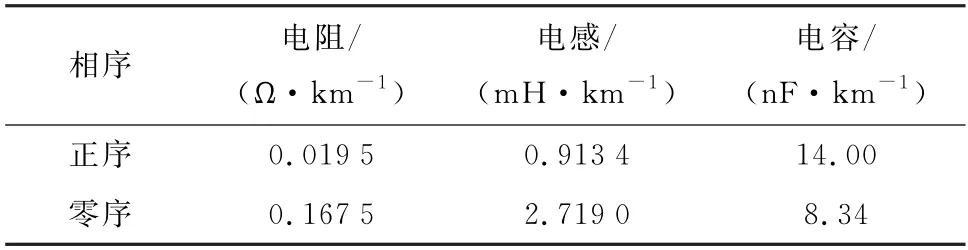
表1 双端带并联电抗器线路参数Table 1 Line parameters

4.2 仿真分析

以双端带并联电抗器的输电线路发生单相接地故障为例,设置两端等效电源电势角差为30°,在距离M 端179 km处A相发生经RF=500Ω接地故障。设置仿真总时长为1 s,故障在0.2 s时发生,故障相断路器在0.22 s时断开,瞬时性故障持续0.2 s,如图4所示;永久性故障一直持续到仿真结束,如图5所示。

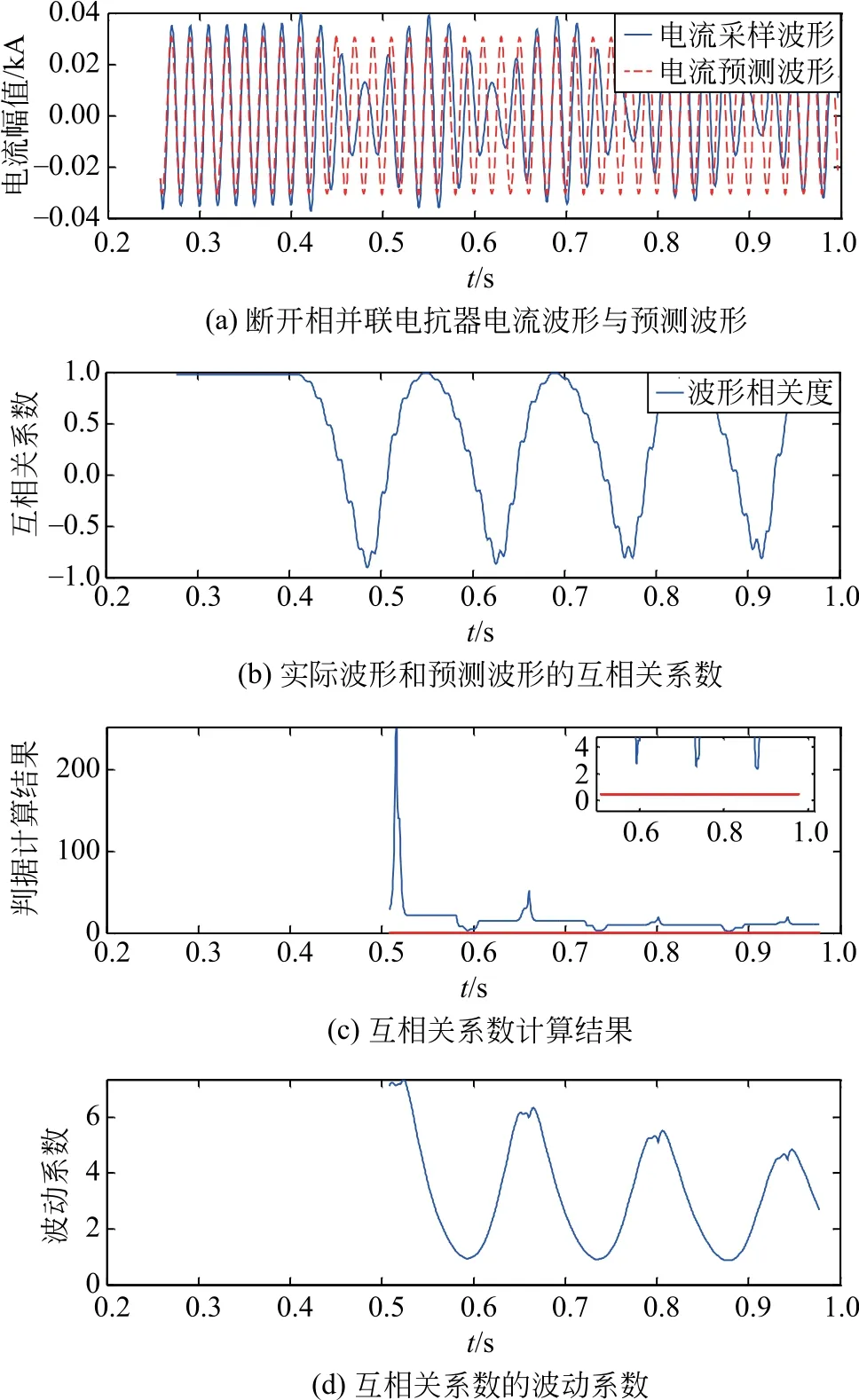
图4 瞬时性故障Fig.4 Transient failure

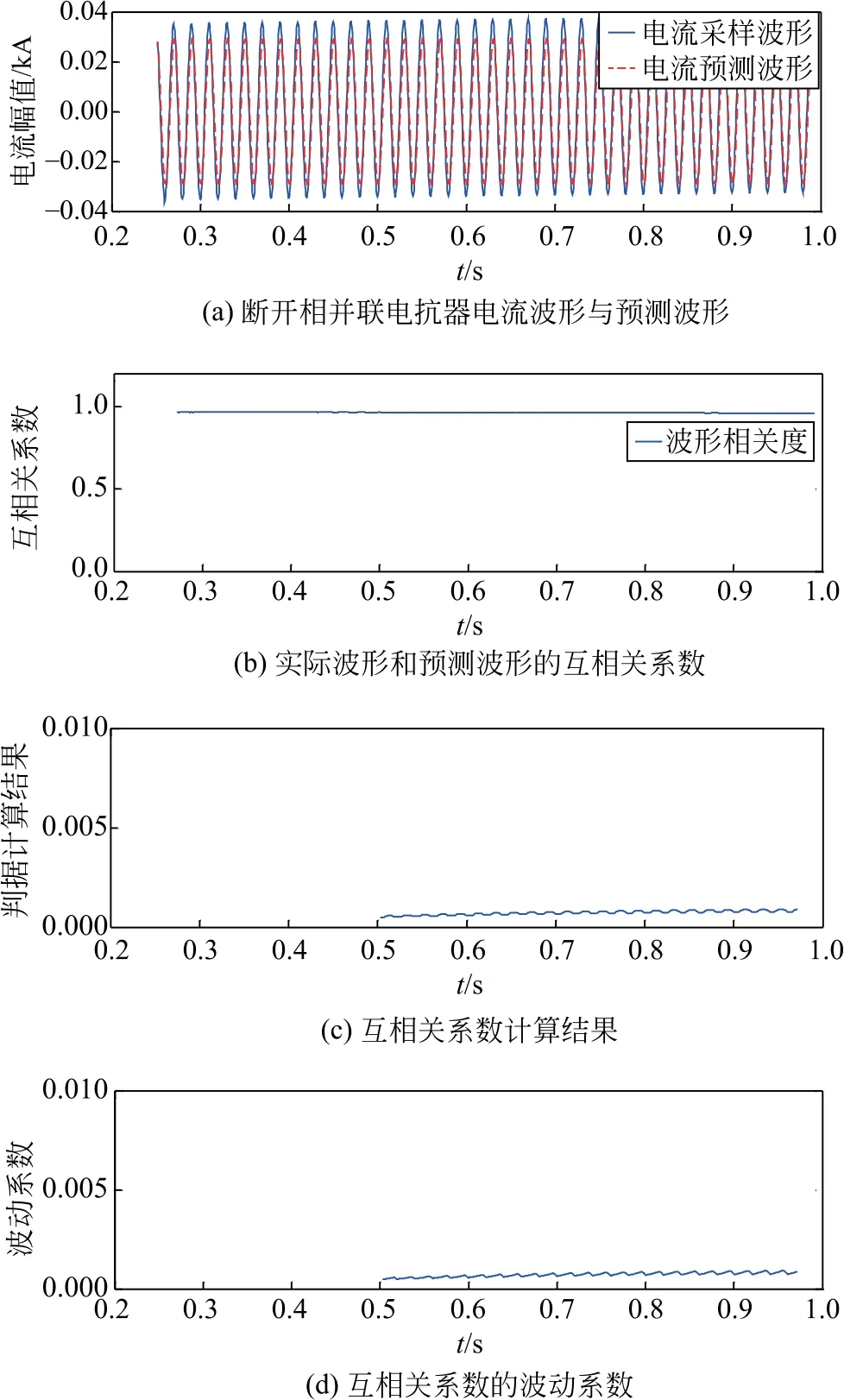
图5 永久性故障Fig.5 Permanent failure

由图4可知,当发生瞬时性故障时,断路器跳闸后的一段时间内,即0.22～0.4 s,断开相并联电抗器电流的波形为正弦波,其实际采样波形和预测正弦波形保持一致,互相关系数为1;在0.4s以后,断开相并联电抗器电流存在拍频特性,其采样波形由正弦波变为包络线上下波动的非正弦曲线,而其预测电流波形为正弦波,因此2种波形的互相关系数波动剧烈,并且随时间呈现周期性的变化,基于互相关系数的判据计算结果如图4(c)所示,其值恒大于整定值k1,满足式(17);互相关系数的波动系数如图4(d)所示,由图可知δ＞0且满足式(18)。

根据上述分析,可判定故障为瞬时性故障,且已经熄弧,因此,可发出允许合闸的命令,进行合闸操作,使故障线路恢复运行。

由图5 可知,发生永久性故障时,断路器跳闸后,断开相并联电抗器电流一直为正弦波,在0.4 s后,断开相并联电抗器电流不存在拍频特性,实际采样波形仍然为正弦波,预测波形也为正弦波,2种波形在幅值和相位上保持一致,几乎重合,呈现正相关,因此二者的互相关系数在1附近很小的范围内波动,基于互相关系数的故障判据计算结果如图5(c)所示,其值约等于0,且恒小于整定值,不满足式(17);互相关系数的波动系数如图5(d)所示,由图可知δ≈0且恒小于整定值,不满足式(18)。

由上述分析可判定故障为永久性故障,因此发出闭锁重合闸命令。

4.3 不同故障情况下的仿真验证

为验证在不同并联电抗器安装位置、不同故障位置和不同过渡电阻下本文所提故障判据的准确可靠性和方法的适用性,对线路双端带并联电抗器的各种故障情况进行仿真。

图6、7为双端带并联电抗器输电线路断开相并联电抗器电流实际采样波形与预测正弦波形互相关系数差动判据计算结果的最大值和最小值。由图可知,在发生瞬时性故障时,由于互相关系数波动剧烈,其判据计算结果的最大值和最小值均大于整定值k1,满足瞬时性故障判据式(17);在发生永久性故障时,互相关系数为1附近的稳定值,其判据计算结果的最大值和最小值均小于整定值k1,不满足瞬时性故障判据式(17)。

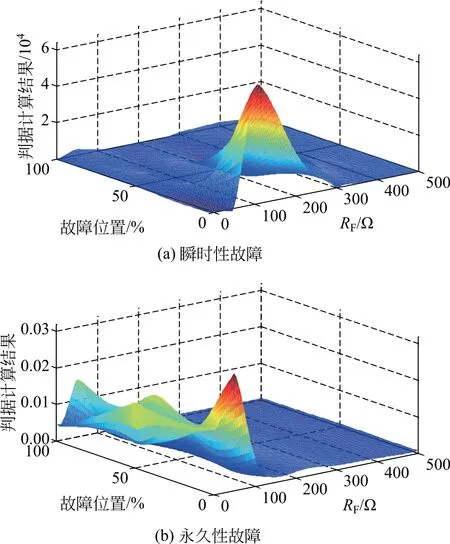
图6 差动判据计算结果最大值Fig.6 Maximum value of differential criterion calculation result

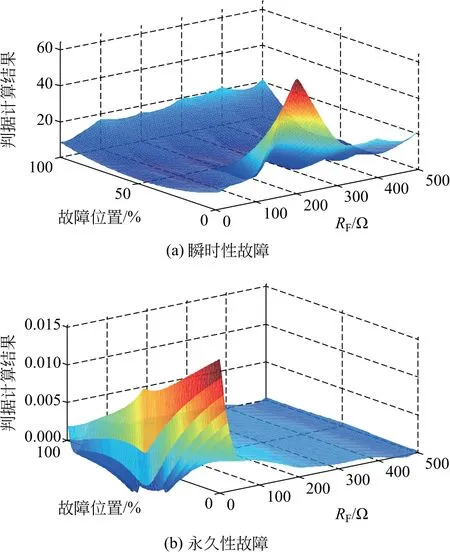
图7 差动判据计算结果最小值Fig.7 Minimum value of differential criterion calculation result

图8、9为双端带并联电抗器输电线路断开相并联电抗器电流实际采样波形和预测正弦波互相关系数的波动系数的最大值和最小值。由图8、9 可知,在发生瞬时性故障时,互相关系数的波动系数较大,其最大值和最小值均大于整定值k2,满足瞬时性故障判据式(18);在发生永久性故障时,互相关系数的波动系数较小,其最大值和最小值均小于整定值k2,不满足瞬时性故障判据式(18)。

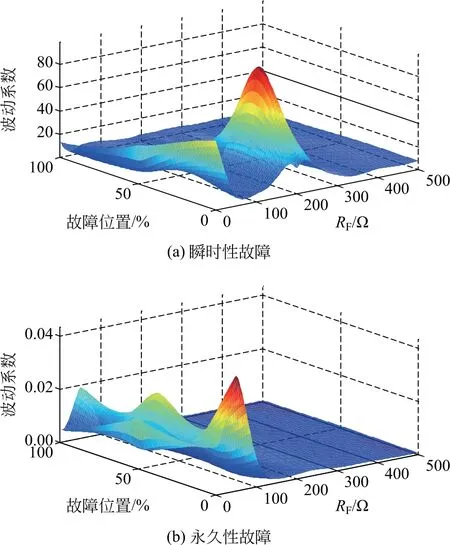
图8 波动系数最大值Fig.8 Maximum fluctuation coefficient

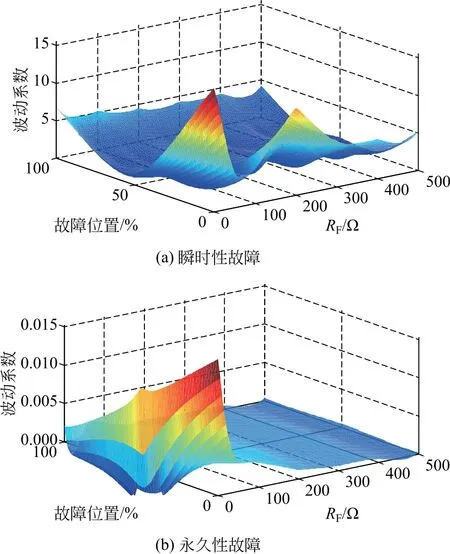
图9 波动系数最小值Fig.9 Minimum fluctuation coefficient

5 结论

本文基于断开相并联电抗器电流在瞬时性和永久性故障下的波形差异性,利用断路器跳闸后的二次电弧阶段符合正弦特征的短数据窗来构造预测波形,将采样得到的实际电流波形和构造的预测波形进行相似度比较,两种波形在瞬时性故障下差别较大,永久性故障下则保持一致;基于波形互相关系数,提出了一种利用断开相并联电抗器电流拍频特性的单相自适应重合闸瞬时性故障识别方法,该方法原理简单,易于实现,对于拍频特性明显的线路更加适合。最后通过PSCAD 搭建500k V 输电线路仿真模型,对不同的故障情况进行了大量的仿真,实验结果充分表明,该方法能够准确地识别出瞬时故障性质。