双碳背景下CCHP 系统运行策略优化

王钟震 乔春珍 刘天笑 李昭君 刘星雨 赵睿杰 万逵芳

(1.北方工业大学土木工程学院,北京市 石景山区 100144;2.中国大唐集团科学技术研究总院有限公司华北电力试验研究院,北京市 石景山区 100040)

0 引言

在3060双碳目标提出后,我国能源行业中各种能源系统的能源利用率和能源减排率等需要达到新的高度[1]。作为一种传统分布式能源系统,冷热电三联供系统(combined cooling heating and power,CCHP)凭借着较高一次能源利用率和高经济性

[2-3],在国外的能源体系中有着较高的占比[3-7]。近些年在国家支持下,我国CCHP 系统发展迅速,CCHP系统的优化运行策略研究受到关注[8-13]。王子铭等[14]建立了基于相变储能热阻模型的CCHP型微能网优化调度模型,减少了系统运行总成本。杨晓辉等[15]建立了涉及综合需求响应的冷热电联供系统双层规划模型,可有效降低系统运行总成本。王智等[16]分别构建了日前优化模型和日内滚动优化模型,并通过该模型设计出能让CCHP更加平滑的运行策略,一定程度提高了整个系统的经济性。但上述关于CCHP系统运行经济性的研究,并未考虑未来可能出现的碳排放成本。随着国内碳交易的发展[15],未来碳排放成本必将影响CCHP系统的经济性和优化运行策略。本文将碳排放成本加入CCHP系统运行成本中,并考虑碳排放价格和碳排放指标两种不同的约束方式,基于Matlab建模,以经济运行成本最低作为优化目标,采用非线性规划法,为CCHP系统提供在双碳背景下可以采用的经济运行策略[17-19],同时也为3060双碳背景下CCHP的发展和应用提供参考。

1 CCHP 系统运行优化模型

1.1 系统构成

某CCHP系统,主要由3 台Capstone公司生产的200 kW 微型燃气轮机(以下简称为C200)、1台吸收式制冷机、3台电制冷机组成,用于承担该单位建筑的冷、电负荷,该CCHP系统的示意图如图1所示,其建筑物的夏季冷、电负荷和典型日冷、电逐时负荷如图2所示。

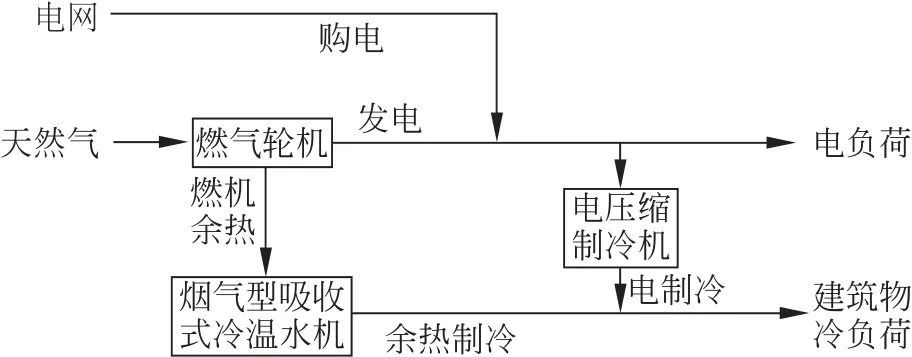
图1 CCHP系统结构图Fig.1 Structure diagram of the CCHP system

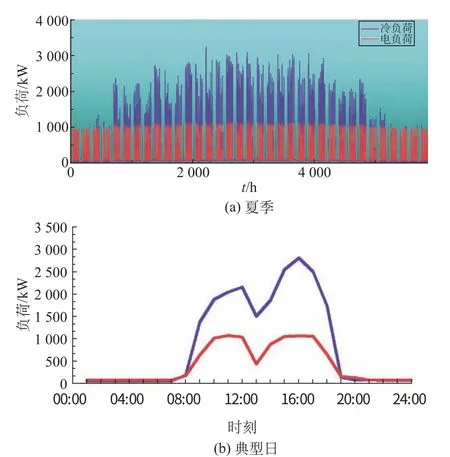
图2 夏季与典型日冷、电负荷Fig.2 Cooling and electric load of summer and typical daily

1.2 设备热工模型

1.2.1 燃气轮机模型

为较准确地模拟C200 的实际运行特性,本文依据设备制造商提供的该燃气轮机变工况数据,通过公式拟合,构建C200燃气轮机数字模型。建模中考虑环境温度、机组负荷率对燃气轮机性能、排烟温度和排烟余热影响。

综上,燃气轮机热力特性的函数表达式为

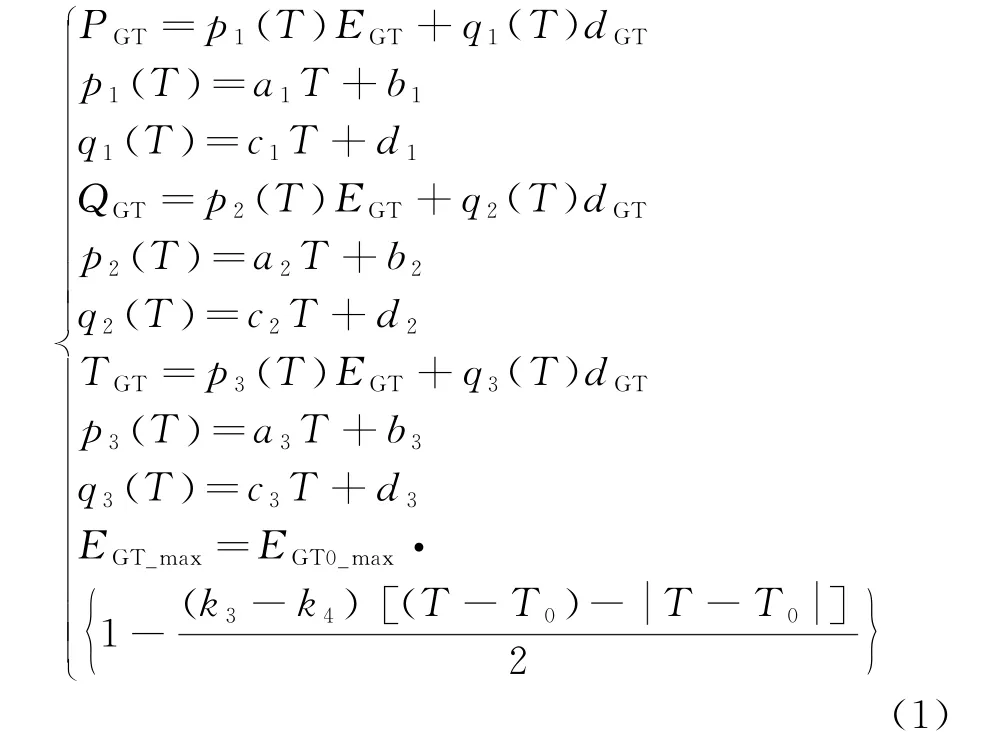
式中:PGT为燃气轮机发电量,kW·h;EGT为输入燃气轮机的燃料热量,kW·h;dGT为运行燃气轮机台数;QGT为燃气轮机排烟的可利用热量,kW·h;TGT为燃气轮机排烟温度,℃;T为燃机工作的环境温度,℃;T0为设计工况温度,取22.96 ℃;EGT_max为燃气轮机满负荷发电量,kW·h;EGT0_max为设计工况温度下燃气轮机的满负荷发电量,kW·h;其他符号如表1所示。

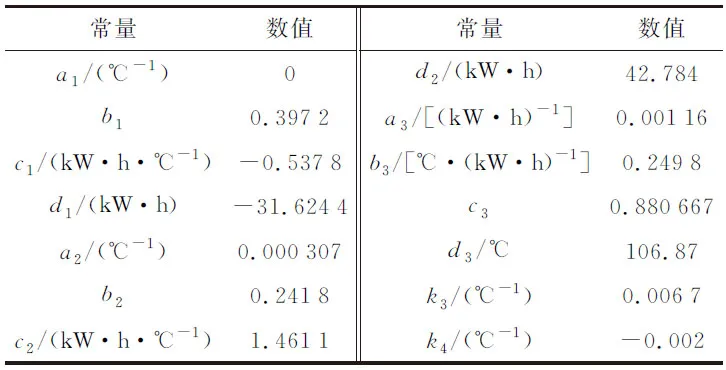
表1 燃机模型中各系数常数Table 1 Each coefficient constant in the gas turbine model

1.2.2 吸收式冷温水机模型

同样,对该系统中吸收式冷温水机进行变工况模拟,对于该燃气轮机联供系统,排烟温度较高,可利用的余热为较高品质的烟气,所以使用双效烟气直燃机。

综上,燃气轮机热力特性的函数表达式为

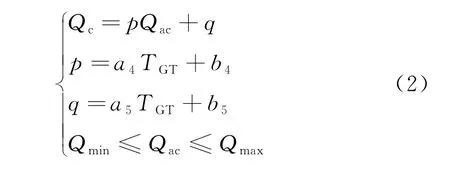
式中:Qc为制冷量,kW·h;Qac为使用烟气热量,kW·h;Qmin、Qmax为输入烟气的最小、最大热量,kW·h;其他如表2所示。

表2 吸收式冷温水机模型中各系数常数Table 2 Each coefficient constant in the absorption cold warm water machine model

1.2.3 电压缩空调模型

电压缩空调模型函数表达式为

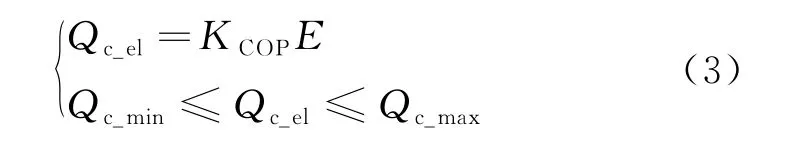
式中:f(x)为运行的逐时成本;Pprice_el(i)为分时电价,元/(kW·h),取23:00—07:00谷段电价0.381 0元/(kW·h);07:00—10:00、15:00—18:00及21:00—23:00,平段电价0.839 5元/(kW·h);10:00—15:00及18:00—21:00,峰段电价1.440 9 元/(kW·h);Eele_purchased(i)为额外购电量,kW·h;Pprice_ng为天然气价格,元/m3;EGT(i)为系统中燃机逐时消耗的天然气的热量,kW·h;KLHV为天然气低位发热量,MJ/m3;H为计算周期小时数;x为所求的最优解。x的表达式为

式中:dac为吸收式冷温水机运行台数;Re为电压缩式空调逐时耗电量,kW。

考虑碳排放成本时,将式(4)中的电价和天然气价格加以修正。其中,电价在当前分时电价基础上增加单位发电量对应的CO2排放成本;天然气价格在当前价格基础上增加单位体积天然气燃烧对应的CO2排放成本,其中对于电价和天然气价格的修正如下:

式中:Qc_el为电压缩空调制冷量,kW·h;Qc_min、Qc_max为电压缩空调最小、最大制冷量,kW·h;KCOP为制冷系数(coefficient of performance,COP),即能效比,根据该单位中央空调电制冷情况选取平均COP为2.8;E为电空调耗电量,kW·h。

1.3 优化模型

1.3.1 运行成本目标函数

不考虑碳排放成本的逐时运行成本为

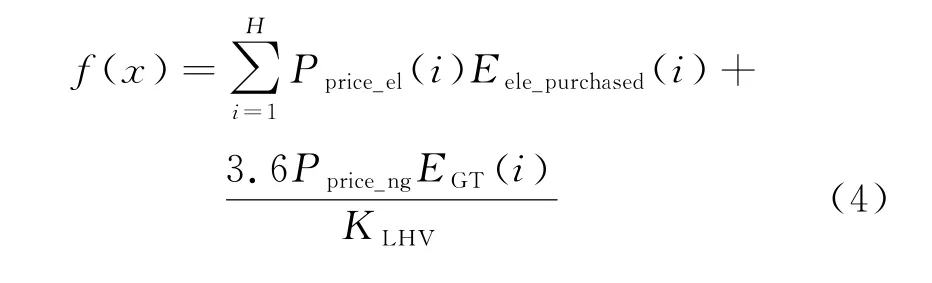
综上所述,最终的逐时运行成本为

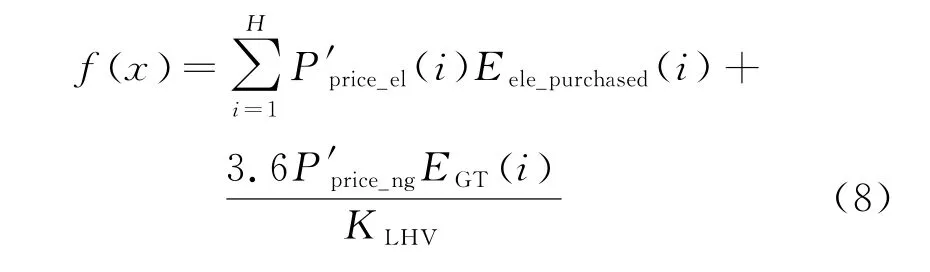
1.3.2 碳排放量目标函数

逐时碳排放量为

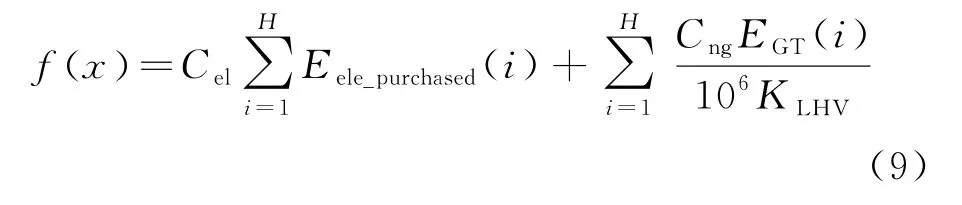
需要说明的是在目标函数中,本案例时间间隔采用1 h,若时间间隔非1 h,则根据时间间隔对结果进行等比例修正,且本案例中电价采取分时电价,在Matlab中体现为含有24个元素的数组。

1.3.3 约束条件

基于Matlab软件工具箱的fmincon和fminconset函数,将上述系统优化运行转换为带约束条件的非线性优化问题求解。

线性不等式约束为

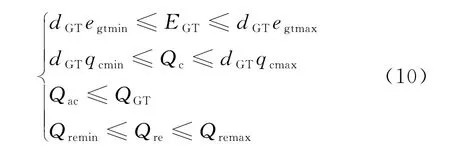
式中:egtmin为单台燃机最小负荷下燃料输入热量,kW·h;egtmax为单台燃机最高负荷下燃料输入热量,kW·h;qcmin为台吸收式机组最小输出冷量,kW·h;qcmax为单台吸收式机组最大输出冷量,kW·h;Qremin为电空调的最小出力,kW;Qre为电空调实际出力,kW;Qremax为电空调最大出力,kW。

线性等式约束条件为

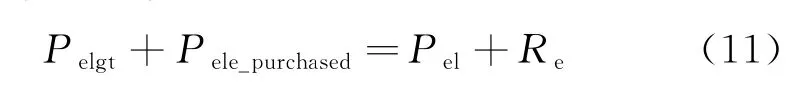
式中:Pelgt为所有运行燃机逐时供电出力,kW;Pel为用户逐时电负荷,kW。

非线性等式约束条件为

式中Q为用户逐时冷负荷需求,kW。

1.3.4 优化计算流程

基于Matlab建立优化数学模型,优化计算逻辑如图3所示。

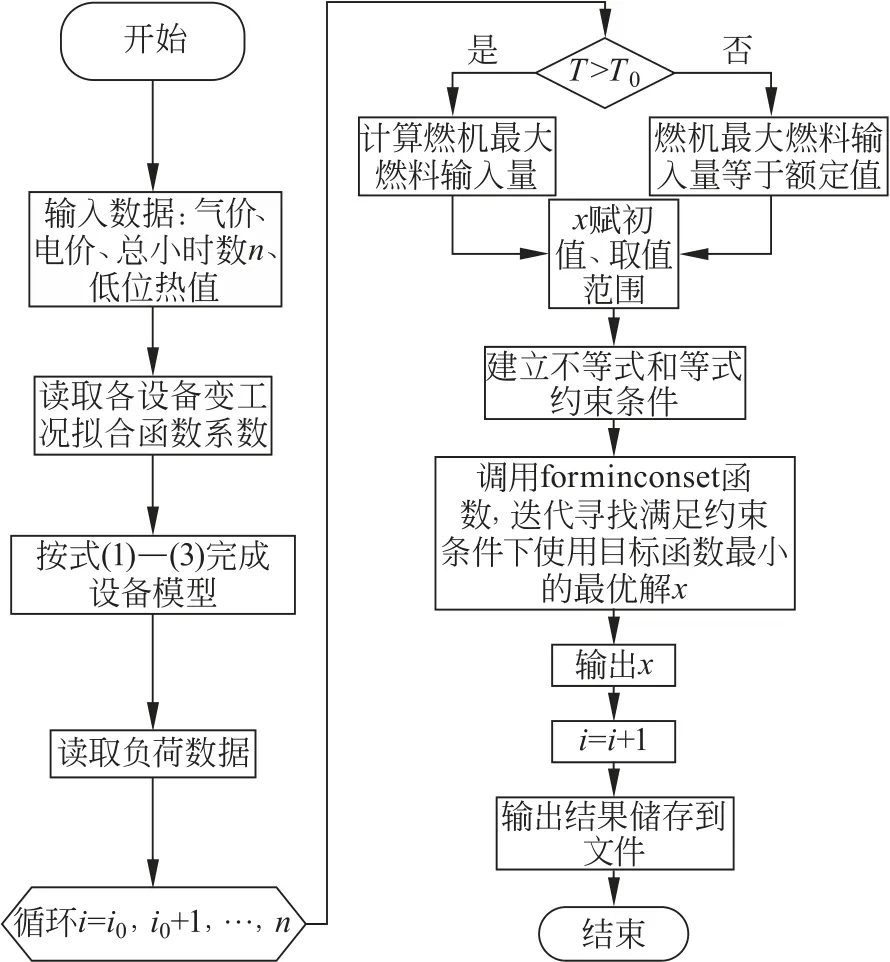
图3 优化计算逻辑图Fig.3 Optimize the calculation logic diagram

2 负荷计算与结果分析

2.1 碳排放价格下成本优化策略

以夏季典型日24 h冷、电逐时负荷为例,在碳排放价格56 元/t条件下,直接将56 元/t带入式(8)进行优化计算,优化结果如图4所示。通过典型日电热负荷规律的分析,发现运行策略整体可分为2个阶段。

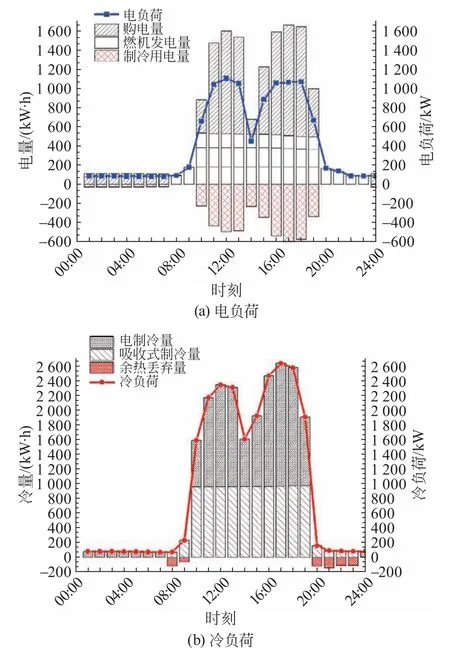
图4 夏季典型日系统优化运行图Fig.4 Optimized operation diagram of system in summer typical day

阶段1 为20:00—09:00,这个阶段该建筑的冷、电负荷较低,均不大于200 kW,存在直接从电网购电承担电热负荷和只开1台燃气轮机发电并通过余热制冷机制冷承担冷、电负荷2种不同的策略,此时策略的选择与该模型模拟时采用的分时电价相关。在23:00—07:00电价处于谷段,购电成本低,在其余时间电价处于平段甚至峰段,购买天然气发电成本低,所以开1台燃气轮机发电并通过余热制冷机制冷。即便上述时段冷负荷低,燃机全部余热制冷量高于用户冷负荷,需要丢弃一部分余热,但此时燃机发电和部分余热制冷成本低于购买同等电量的成本,经济性仍然良好。

阶段2为10:00—19:00,这个阶段的整体冷、电负荷较高,其中电负荷均高于600 kW,冷负荷均高于1 000 kW,3台C200满负荷运行,全部余热量均用于制冷。如图4(b)所示,上述时段所有余热用于制冷,仍不足以满足用户冷负荷,多余冷负荷需要电制冷压缩机承担,在负荷形式上体现为从冷负荷向电负荷的转化,所以在图4(a)中可明显看到10:00—19:00购电量与发电量之和是远大于用户电负荷的,以14:00为例,此时的电负荷低于3台燃机最大发电量,但仍需额外购电,正是因为此时余热制冷量不足,冷负荷通过电制冷压缩机转化为电负荷导致整体阶段2的余热制冷量不足,需要通过提高吸收式冷温水机效率和增大余热量来改善。

通过对计算结果的逐时分析,发现阶段1出现余热量丢弃,阶段2出现余热量不足,若能将阶段1余热量储存到阶段2使用,可进一步节约成本和降低系统的碳排放量;同时,通过图4可看到模型给出的运行策略与算例负荷拟合良好,验证了模型的正确性、可靠性和实用性。

2.2 碳排放指标下运行优化策略

Matlab建模时采用逐时优化的算法,但碳排放指标属于整个周期碳排放量的约束,很难做到逐时优化求解。故首先改变目标函数,采取式(9)以碳排放量最低作为优化目标,得到在总周期内为满足用户冷、电负荷需求的最低碳排放量,为1 815.26 t。基于最低碳排放可以分为两种情况:

(1) 若规定的碳排放指标低于该值,则需要进一步降低碳排放总量,要么购买更多绿电,要么更换效率更高的设备。

(2) 若规定的碳排放指标高于该值,则在不同碳排放价格下,进行以运行成本最低为目标的优化计算,并得出在该碳排放价格下的周期碳排放量与周期运行成本,如图5所示。用户可根据要求的碳排放指标查取到对应的碳排放价格,例如:碳排放指标为1 900 t时,可以采用110元/t碳排放价格下的运行策略,在图5中查得110元/t碳排放价格下的周期碳排放量为1 896.83 t,符合碳排放指标。于是把1 900 t碳排放指标的运行约束条件转换为110元/t碳排放价格下的运行约束条件,并将110 元/t带入式(8),即可得到满足1 900 t碳排放指标下的运行优化策略。

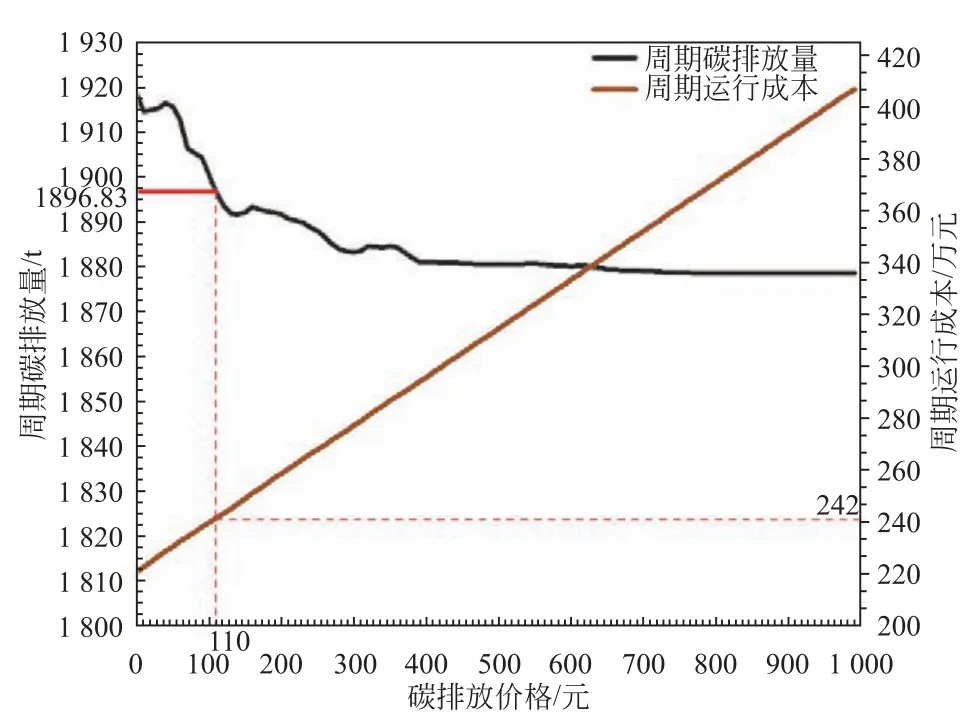
图5 不同碳排放价格下周期碳排放量与运行成本Fig.5 Cycle carbon emissions and operating costs under different carbon emission prices

3 结论

(1) 通过Matlab软件建模计算,该数学模型可为已经确定配置和负荷的CCHP 系统提供在碳排放价格下或碳排放指标下的成本最低的逐时运行策略,并通过实际算例进行优化模拟,发现该模型提供的运行策略与实际负荷拟合良好,实用性强。

(2) 通过本模型对算例中CCHP系统在不同碳排放价格下进行优化运行,发现在优化目标为运行成本最低情况时,其周期碳排放量受碳排放价格影响而降低,在400 元/t的范围内下降幅度比较明显,在400元/t以上降速变缓甚至趋于水平。