基于最优路径的多微网能源调度研究

张 羽李春华马浩东付林瑶

(江苏科技大学自动化学院,江苏省 镇江市 212114)

0 引言

多微电网之间的能源交互可实现更广阔的能源调度,并且能在更大程度上提高能源利用率,提高供电可靠性[1]。同时,多微电网系统中的单微电网只有满足了自身的能量需求之后,才能参与多微网间的能量互济,这样可提高单一微电网独立运行过程中抗干扰能力和避免不必要的能量交互等问题[2-4],最终实现整个多微网系统的安全高效运行。

多微网系统具有稳定、安全的特点,目前已有很多学者对其进行了研究。文献[5]提出了一种上下层优化调度模型,上层调度对不同时间段的负载进行划分,建立相应模型,下层调度目标函数为微电网调度成本最小,考虑分时电价并使用粒子群算法进行求解;文献[6]提出了一种分布式能量管理策略,通过配置微电网能量管理系统的方式进行电力信息交换和运营,实现多微电网对分布式电源的有效管理,并采用交替方向乘子法对成本问题进行迭代求解,然而忽略了交互过程中的能量损耗;文献[7]构建了微电网电量与电价的竞标模式,以最小的成本作为投标电价,而投标电量考虑系统能够承受的最大风险比例,以此依托价格的差异和时间的惯性权重实现智能配电网的快速调度,然而只考虑了多微电网系统与配电网之间的整体交互功率,并没有考虑微电网与微电网间的交互功率;文献[8]构建了多目标优化模型,把微电网间功率交互时的交易电价作为优化变量之一,构造运行成本最小的目标函数,考虑储能系统、柴油发电机以及微电网间和电网与微电网间的交互功率成本,使用非支配排序遗传算法求解,然而却忽略了微网运行时的环境效益;文献[9]构建了一种计及负荷需求与多微网间功率互济的优化调度模型,并且全面考虑了风、光清洁能源发电的维护成本、燃气轮机的燃料费用、蓄电池的损耗成本、微电网与大电网功率交互产生的购电成本以及出售电的收益,却没有考虑交互过程中的能量损耗。

基于以上分析,本文在微电网并网运行的运行条件下,建立并网型多微网系统双层优化调度模型,第1层调度以维护费用、燃料费用、蓄电池损耗费用、污染物治理费用及功率交互费用最低为目标函数;采用群集蜘蛛优化算法求解第1层1个周期内各分布式发电单元的最优出力及总运行成本。第2层调度在第1层调度的优化结果之上考虑各微电网之间以及与大电网之间能量调度的损耗,以各电网之间交互成本最低为目标函数,采用蚁群算法选择损耗最小的最优路径,实现多微网间的能量互济。最后采用基于IEEE 9节点的并网型多微电网系统进行能源调度验证。

1 微电网数学模型

微电网由光伏电池(photovoltaic,PV)、风力发电机(wind turbine,WT)、微型燃气轮机(micro turbine,MT)、蓄电池(storage battery,SB)构成,并与大电网进行电量双向流动[10-11]。

1.1 风力发电机的数学模型

在微电网的优化调度中,需要风力发电机有功功率预测数据,风力发电机的功率输出与风速有关,风力发电机的风速-功率特性曲线可通过多项式拟合得到,即

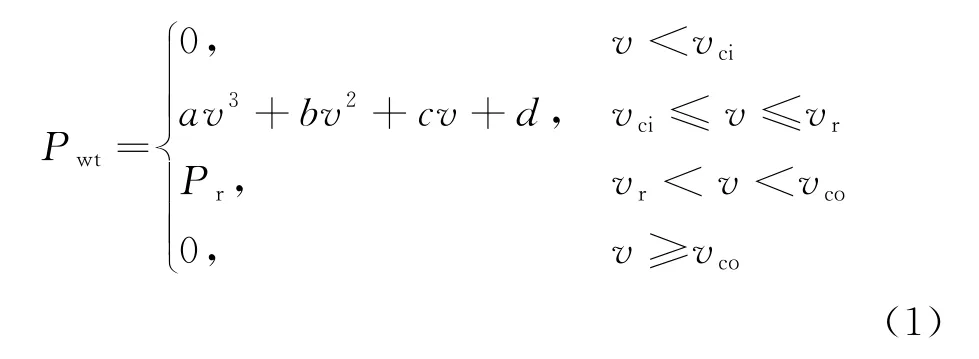
式中:Pwt为风力发电机的输出功率,kW;Pr为风力发电机的额定功率,kW;vci为风力发电机的切入风速,m/s;vr为额定风速,m/s;vco为切出风速,m/s;a、b、c、d为风速参数;v为实际风速,m/s。

在实际优化调度中,为获得较为准确的风力发电机功率预测数据,需要根据实际环境条件对风速-功率特性曲线进行修正。气象局提供的风速数据通常都是在9 m 的高度上得到的,而风速-功率曲线需要提供风机轮毂高度处的风速,因此,必须将其折算成风机轮毂处风速。折算公式如下:

式中:H1、H2为不同的高度,m;v1、v2为不同高度上的风速,m/s;α为幂律指数。

1.2 光伏发电的数学模型

微电网优化调度过程中,需要对光伏电池一整天的输出功率进行预测。光伏电池的功率输出模型为

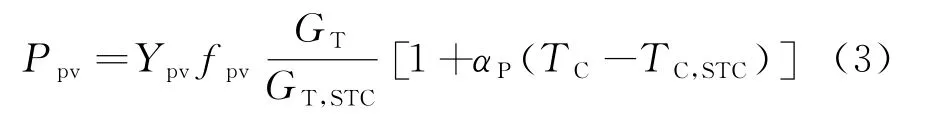
式中:Ppv为光伏电池的输出有功功率,kW;Ypv为光伏电池在标准测试条件下的输出功率,kW;fpv表示光伏列阵上的尘土和积雪等对其的遮挡;GT为当前的太阳辐照强度;GT,STC为标准测试条件下太阳的辐照强度;αP为光伏电池板的功率温度系数;TC为当前的光伏电池温度;TC,STC为标准测试条件下的光伏电池温度[12]。

1.3 蓄电池的数学模型

蓄电池的荷电状态(state of charge,SOC)是电池的重要参数,表示蓄电池当前剩余总能量与电池最大能量的比值:

式中:Q为电池当前剩余能量;Qmax为电池最大能量。

放电深度(depth of discharge,DOD)与荷电状态的关系为

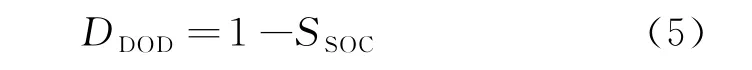
1.4 微型燃气轮机的数学模型

微型燃气轮机的运行效率与其输出的有功功率有关,其数学模型为

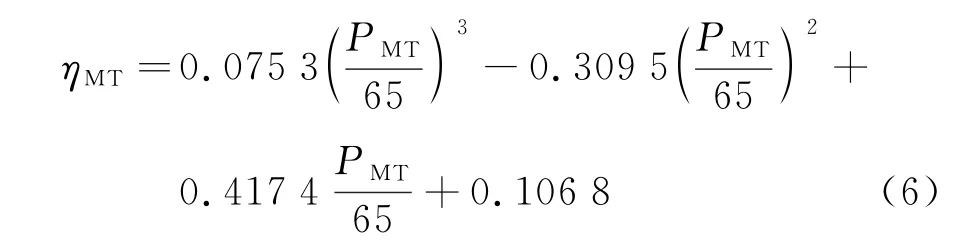
式中:ηMT为燃气轮机的运行效率;PMT为微型燃气轮机输出的有功功率。

2 第1 层多微电网优化调度模型

2.1 微电网系统结构

本文的单微网系统由风力机发电系统、太阳能发电系统、储能系统和微型燃气轮机发电系统及负荷5个部分组成。

2.2 目标函数

在分析系统中各分布式电源的出力情况后,考虑微电网调度周期内的燃料成本、维护成本、蓄电池损耗成本和污染治理成本最低,所建立的总目标函数为

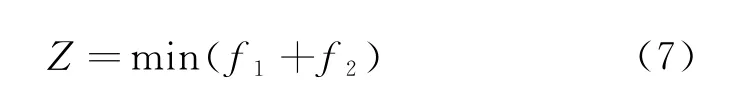
式中:目标函数f1、f2分别为微电网运行成本和环境保护成本。

运行成本包括4个部分:维护费用、燃料费用、交互费用以及蓄电池损耗费用。

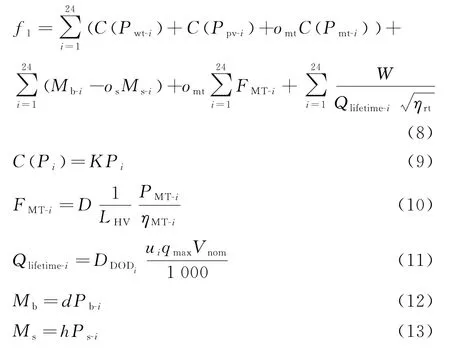
式中:Pwt-i、Ppv-i、Pmt-i分别为风力发电机、光伏发电机和微型燃气轮机在ih里输出的功率;C（P i）为可再生发电单元的维护费用;K为可再生发电单元的维护系数;FMT-i为微型燃气轮机在第i小时的燃料成本;LHV为天然气的低热热值;D为燃气轮机的燃料气体单价;W为蓄电池的购买成本;Qlifetime-i为蓄电池的全寿命输出量;ηrt为蓄电池的往返效率;ui为蓄电池的疲劳循环量;DDODi为蓄电池的放电深度;qmax为蓄电池的最大容量;omt为微型燃气轮机的启停状态;Pb-i、Ps-i为交互功率;d、h分别为买电和卖电的价格系数;Mb、Ms分别为微电网向大电网买电和卖电的费用。

微电网环境保护成本为

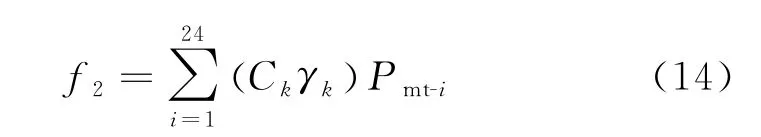
式中:Ck为k类污染物的成本系数;γk为k类污染物的排放量。

2.3 约束条件

功率平衡约束为

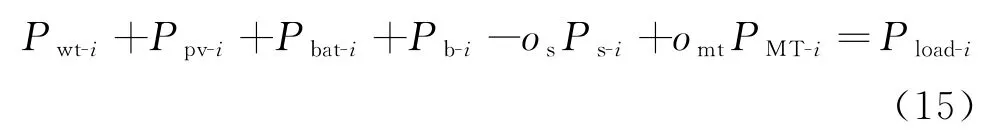
微型燃气轮机出力约束为

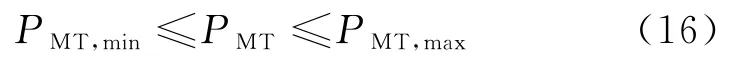
蓄电池充放电约束为

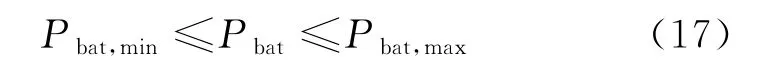
2.4 群集蜘蛛优化算法

在群集蜘蛛优化算法中,空间就像一张蜘蛛网,每只蜘蛛所在的位置被当做一个备选解,并且依靠蜘蛛的适应度值的大小来决定每只蜘蛛的权重大小。蜘蛛个体之间通过分工合作、信息交流和繁衍后代等行为对所需解决问题的最优解进行搜索[13-14]。

2.4.1 种群初始化

种群初始化包括种群数目N,并计算婚配半径r和雌蜘蛛数目Nf和雄蜘蛛数目Nm。

2.4.2 雌性种群协作过程

雌性蜘蛛通过自身振动吸引其他个体向其靠近或者远离,其位置更新如下:

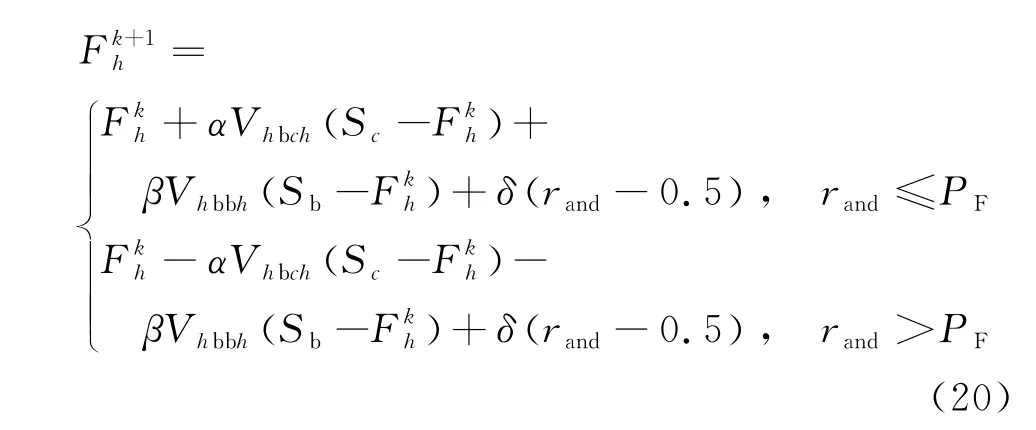
式中:α、β、δ为[0.1]之间的随机数;PF为概率因子;Sc为权重高于自身且距离最近的雌性个体;Sb为全部雌性蜘蛛中拥有最高权重的个体;Vhbch为蜘蛛h对蜘蛛c的震动感知能力;Vhbbh为拥有最高权重的蜘蛛对蜘蛛h的感知能力。

2.4.3 雄性种群协作过程

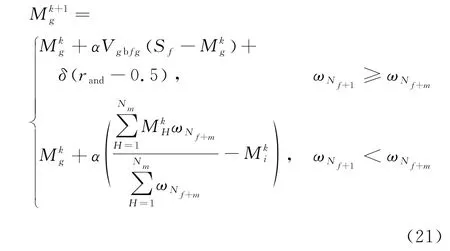
式中:Sf为距雄性支配个体g最近的雌性蜘蛛个体f所在的位置;Vgbfg为雄性个体g对个体f的振动感知能力表示雄性种群的中心位置。

2.4.4 婚配行为

对于权重较高的雄性支配个体g,如果其他的雌性个体处于它的婚配范围内,即满足个体g和个体l之间的欧式距离dgl≤r,g∈TD,l=1,2…,Nf,则发生婚配行为。婚配过程中,婚配蜘蛛越重对产生的子代蜘蛛影响越大。

3 第2 层多微电网优化调度模型

第2层优化调度是在第1层优化的结果之上,将孤岛微电网连接在一起构成多微网系统与大电网共同进行调度,并考虑能量调度过程中的损耗,选择网损最小的路径进行电网间的功率互济。

3.1 目标函数

在各单微网完成内部自身优化之后,只需考虑微网与微网及微网与电网之间功率交互的损耗。

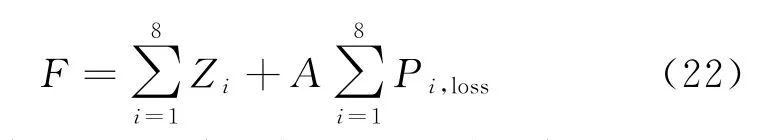
式中:Zi为各微电网单独优化的成本,其中要考虑第2层调度过程中实际的调度情况;A为电网间的交互系数;Pi,loss为各微电网交互过程中的网损。

3.2 约束条件

功率平衡约束为

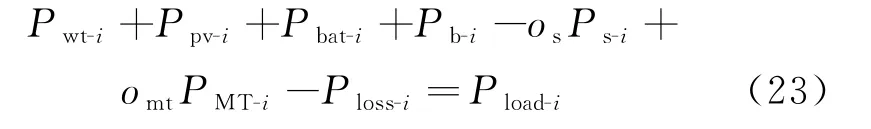
交互功率约束为

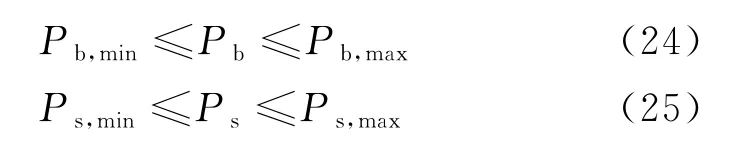
3.3 蚁群算法

蚁群算法是模拟蚂蚁在自然界中寻找食物过程的一种仿生算法。蚂蚁在寻找食物的路径上会释放出一种分泌物质,这种物质使其他的蚂蚁向着这一方向前进,这种在蚁群中能够产生正反馈作用的物质通常称为信息素[15-16]。

3.3.1 状态转移概率

人工蚂蚁在寻找最优过程中,根据不同路径上信息素含量和启发式信息来计算状态转移概率:

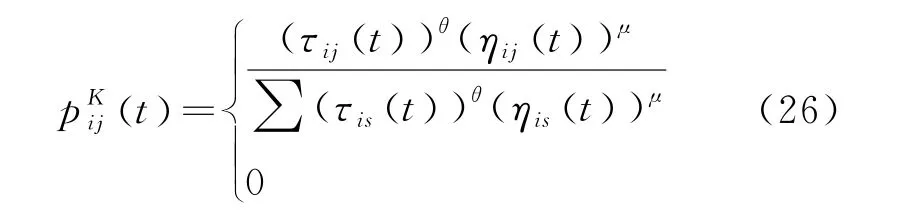
3.3.2 信息素更新

为使蚂蚁在经过所有微电网之后留下的信息素所含信息有效,对遗留的信息素按下式进行更新:

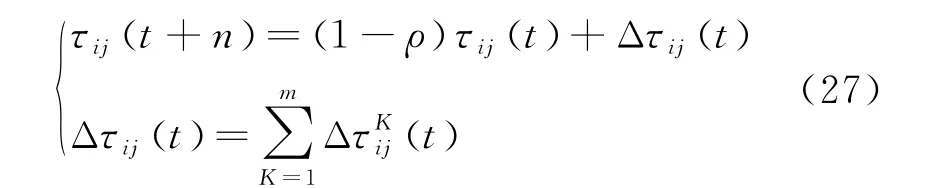
式中:ρ为信息素挥发系数;为第K只蚂蚁在本次循环中留在微电网i与微电网j之间路径上的信息量。

4 算例分析

本文使用基于IEEE 9节点的微电网系统进行分析[17],结构如图1所示,其中节点1为大电网,其余节点为微电网。由ENTSO-E 网站提供的数据进行多微网系统的优化调度。各节点间的阻抗大小如表1所示。

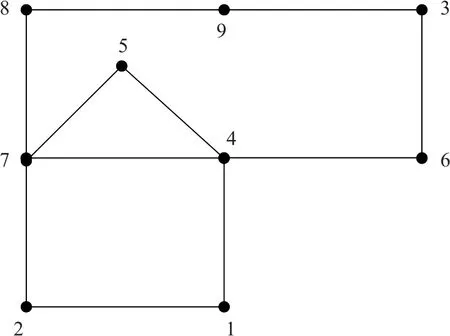
图1 多微网系统结构Fig.1 Multi-microgrid system structure

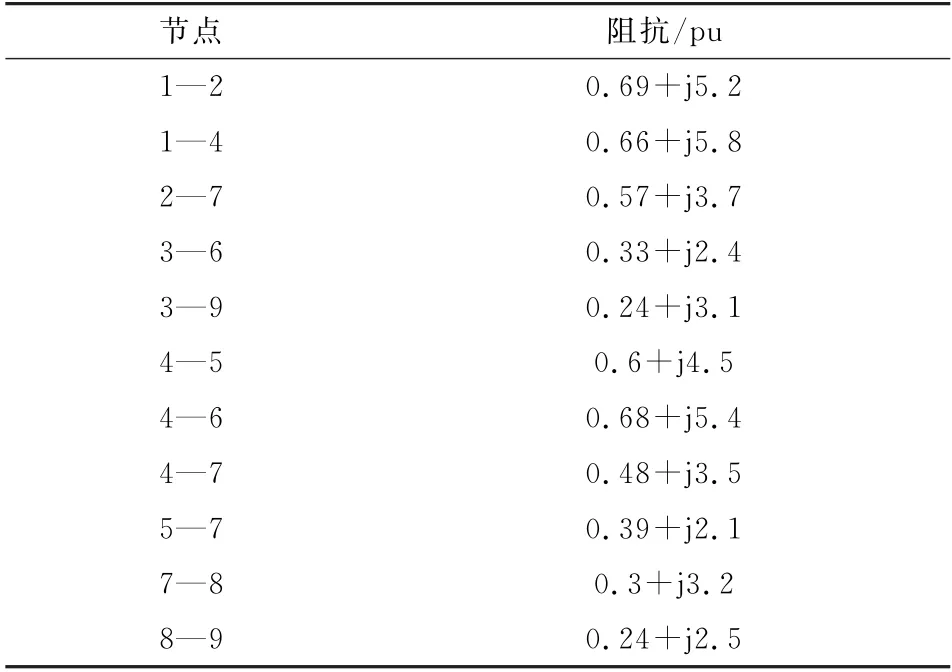
表1 节点间阻抗Table 1 Impedance between nodes

4.1 光伏发电基础数据

光伏电池基础数据如表2所示。

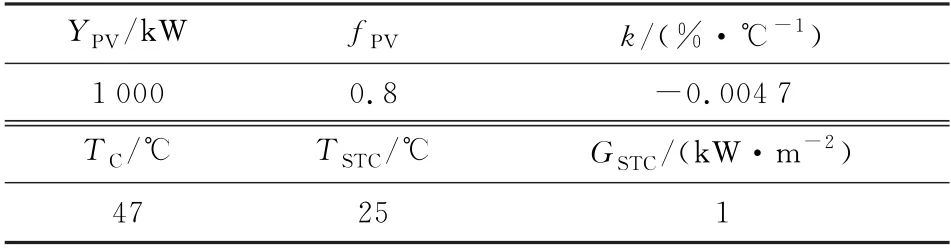
表2 光伏发电基础数据Table 2 Basic data of photovoltaic power generation

4.2 风力机发电基础数据

在Matlab上对风速-功率特性曲线进行曲线拟合,求得的风速参数如表3所示。

表3 风力发电机基础数据Table 3 Basic data of Wind turbine

4.3 蓄电池的基础数据

蓄电池损耗需计算疲劳循环量u,表4为本文使用锂电池的疲劳循环量。对数据进行拟合,得到拟合方程为u=3 491.34DDOD2-8 479.61DDOD+6 539.24。图2为拟合曲线与原数据的对比,从图2可知,拟合效果较好。

表4 锂电池的疲劳循环量表Table 4 Fatigue cycle scale of lithium battery

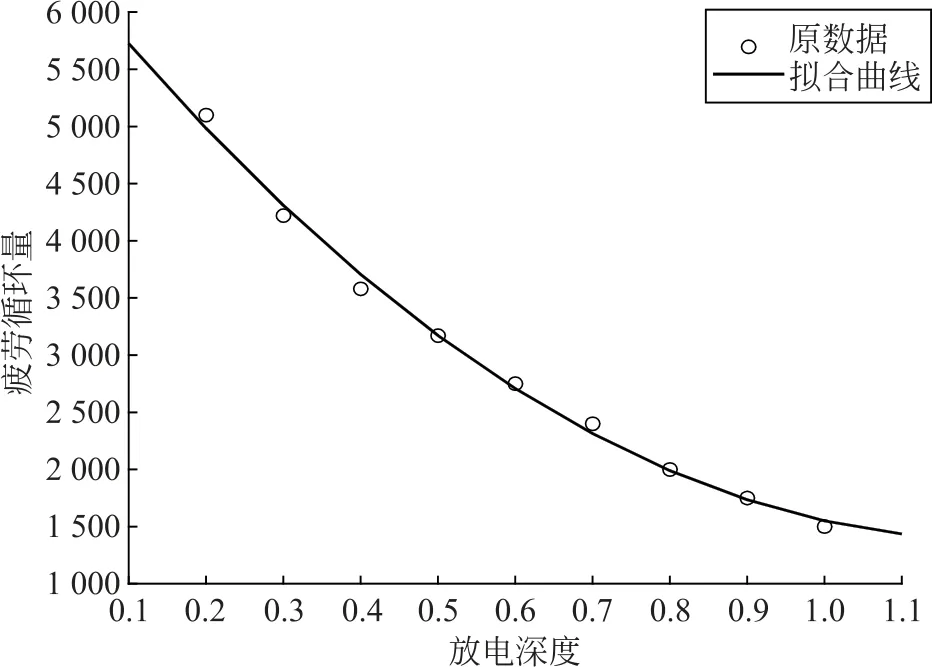
图2 锂电池的疲劳循环量拟合对比图Fig.2 Fatigue cycle fitting comparison of lithium batteries

4.4 微电网仿真基础数据

各发电系统的维护系数如表5所示,污染物排放系数及成本如表6所示。

表5 维护系数表Table 5 Maintenance coefficient table

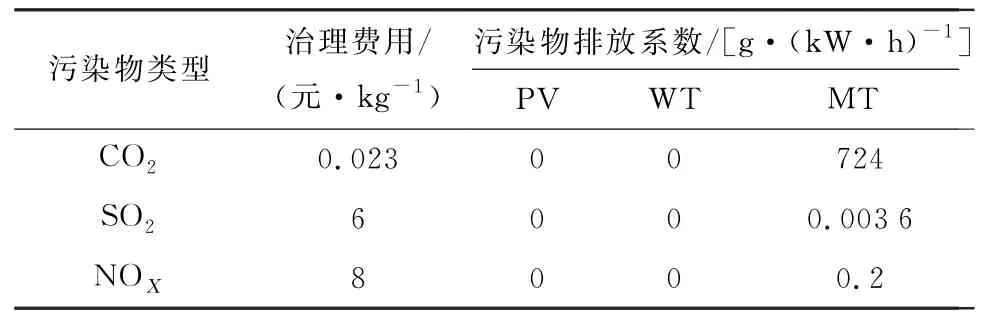
表6 污染物排放系数及成本Table6 Discharge coefficient and cost of pollutants

从大电网和微电网购电的电价如图3所示,出售给大电网和微电网的电价如图4所示。

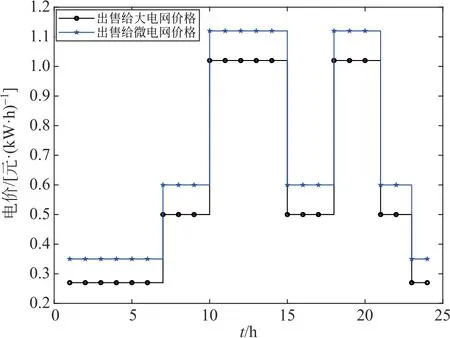
图4 售电价格Fig.4 Prices of power sell

由图3、4可见:23:00—07:00为谷时段,购售电价格最低;07:00—10:00、15:00—18:00及21:00—23:00为平时段;10:00—15:00和18:00—21:00为峰时段,购售电价格最高。

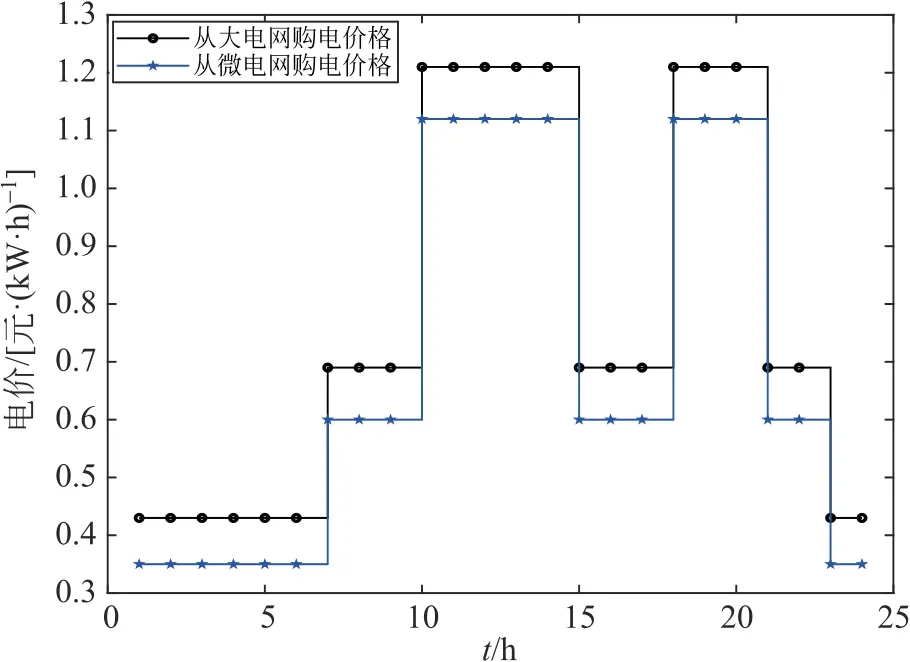
图3 购电价格Fig.3 Prices of power purchase

4.5 多微电网系统优化调度仿真

图5为各微电网光伏、风力机功率及负荷需求的预测数据。各微电网优化调度结果如图6所示。

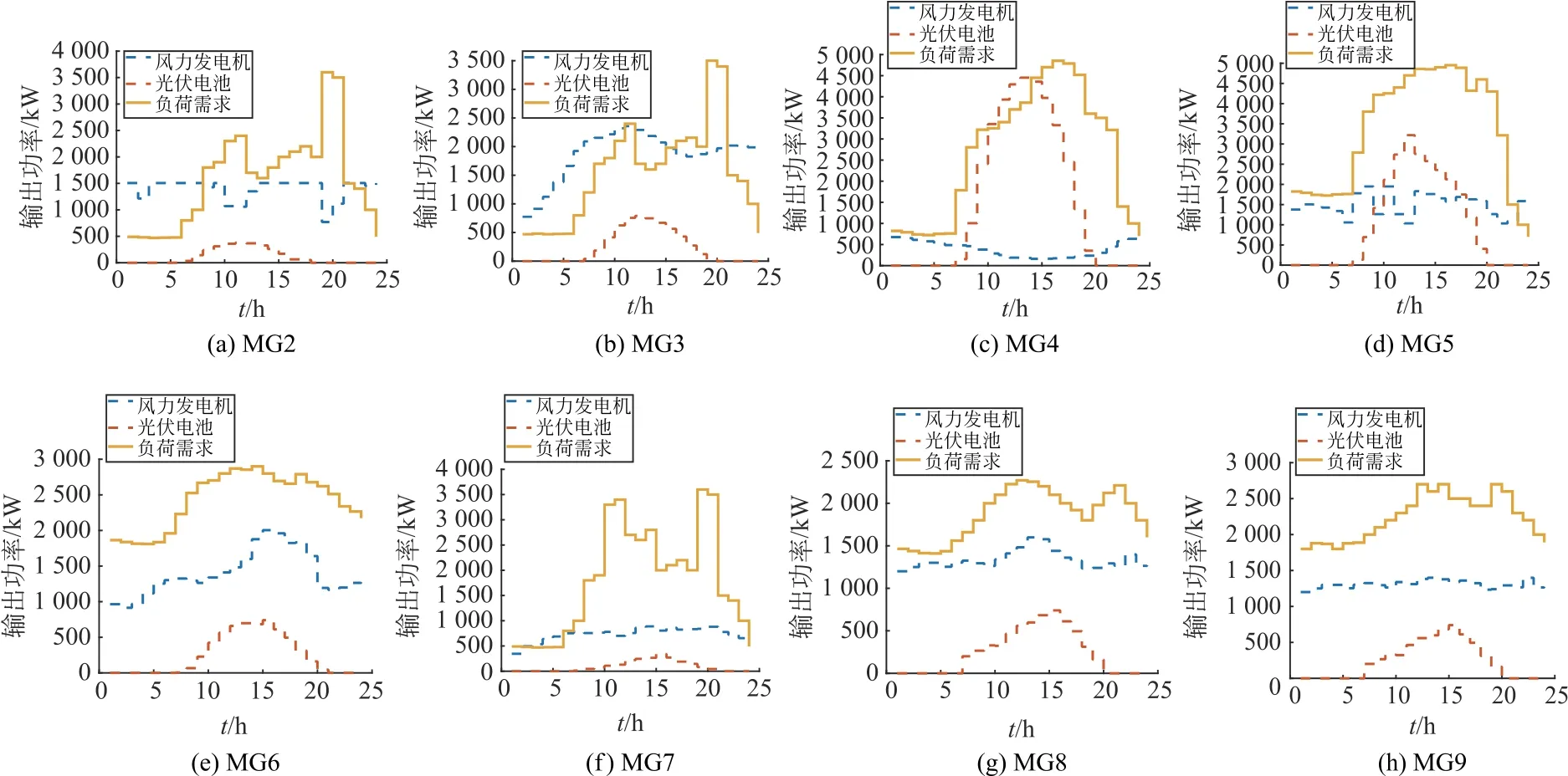
图5 微电网2—9光伏、风力机功率预测数据和负荷需求预测量Fig.5 PV and fan power forecast data and load demand forecast for MG2—9

由图6可看出:多微电网系统在优化调度时,会优先使用风力机和光伏电池所产生的清洁能源;在清洁能源能够满足需求的情况下,优先向蓄电池进行充电,多余的电量会用来进行多微电网能量交互;在清洁能源无法满足需求时,在调度过程中会考虑分时电价,选择购买或者使用蓄电池及燃气轮机来填补需求的空缺。

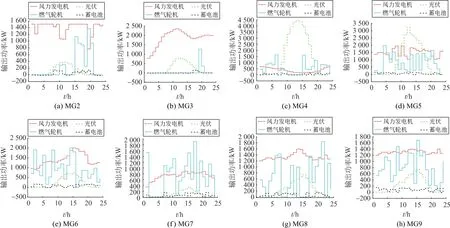
图6 微电网2—9各发电单元优化调度结果Fig.6 Optimization results of each power generation unit for MG2—9

大电网与各微电网之间的交互电量如图7所示。

考虑最优路径之后,大电网与多微网系统中各微电网之间的交互电量如图8所示。

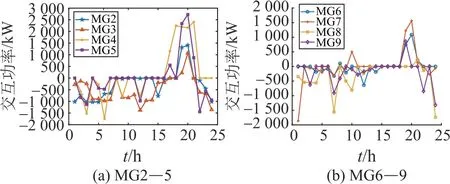
图8 大电网与多微网系统交互电量Fig.8 Electric quantity of interaction between large grid and multi-micro grid system

由图7、8可看出:在多微网系统中,由于大电网昂贵的分时电价以及买卖电过程中的损耗,各微电网更倾向于彼此之间交易,大多数时间与大电网并无能量的交换,这样不但可减小能量损耗,还可节约成本。

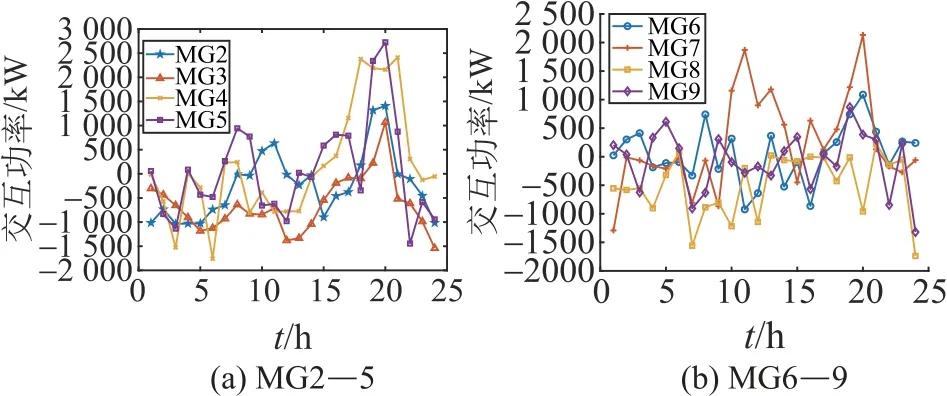
图7 大电网与各微电网交互电量Fig.7 Electric quantity of interaction between large power grid and each microgrid

多微网系统调度过程中的最优路径如表7 所示,总网损和总成本如表8所示。

表7 最优调度路径Table 7 Optimal scheduling path

由表8可知:在各微电网单独调度时,系统的总成本为17 578元,总网损为1 379 kW;而在考虑最优路径的多微网能量调度中,由于调度过程中损耗减小以及多微网间买卖电的价格与大电网不同,多微网系统的总成本为13 443元,总网损为905 kW,网损降低了34.4%,成本降低了23.5%。

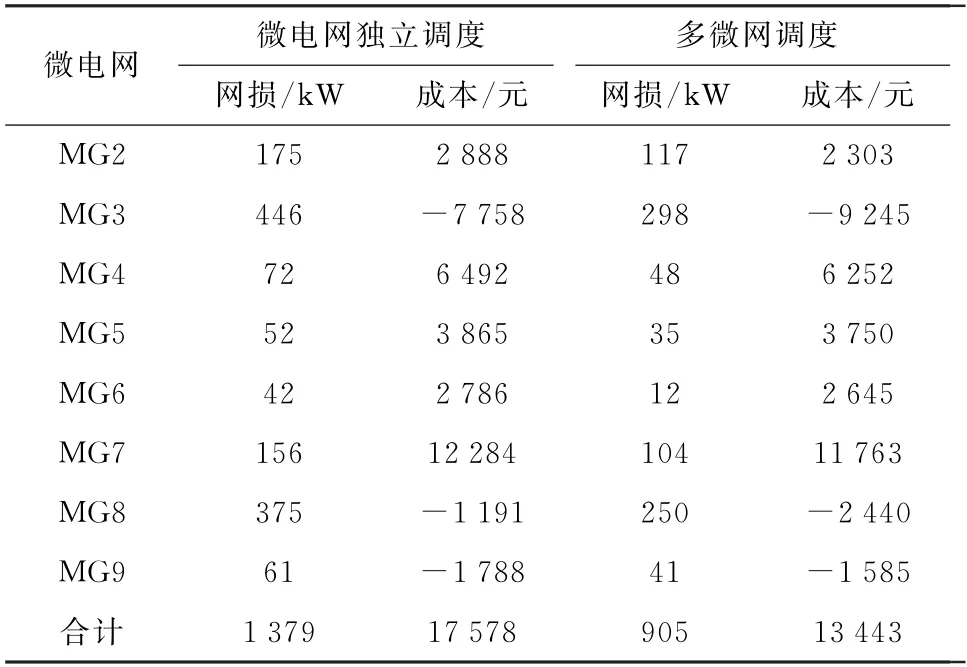
表8 总网损及总成本Table 8 Total network loss and total cost

5 结论

本文考虑多微网间能量互济的最优路径,以IEEE 9节点系统为例进行求解,讨论了微电网单独调度和多微网调度两种模式下的不同结果。通过算例分析,得到以下结论:

(1) 将多微网系统进行双层调度,综合考虑了运行成本、维护成本、环境保护成本及网损的大小,通过智能优化算法求解目标函数,使系统具有较强的鲁棒性和经济性。

(2) 采用最大化清洁能源的调度策略,提高了清洁能源的利用率。

(3) 调度过程中考虑了各微电网及大电网之间的最优传输路径,能够有效地减小传输过程中的功率损耗,达到节约能源的目的。