基于机器学习软骨细胞的时间依赖性力学行为及本构参数反演1)

魏新宇 桑建兵 张睿琳 王静远 刘宝友

(河北工业大学机械工程学院,天津 300401)

引言

软骨细胞稀疏分布于构成软骨的细胞外基质ECM 内,负责ECM 的维护和修复[1-2],其感知到的机械信号能够调节关节软骨的生理机能[3-4].此外,已有研究表明,软骨细胞在不同的病理或生理过程中表现出一定的特征反应,如骨关节炎软骨细胞较正常软骨细胞的黏弹性特性存在明显差异[5],以及在自然生长过程中的软骨细胞整体黏弹性和恢复变形的能力受年龄因素影响发生改变[6].因此,准确量化单个软骨细胞的力学特性及其对机械负荷的响应对于揭示软骨生物力学特性与骨性关节炎病理十分重要.

近年来,力学表征实验技术的发展为推导描述软骨细胞材料特性的本构模型提供了数值基础.研究表明,软骨细胞表现出高度非线性弹性[7-8].Florea 等[9]基于纳米压痕实验和计算建模,揭示了软骨细胞随时间变化的力学行为的关键本构参数.文献[10-11]基于微管抽吸实验的数值模拟及理论分析探讨了软骨细胞半空间模型、不可压缩球体模型和可压缩球体模型的弹性参数的差异.文献[12-13]基于无侧限压缩试验探究了软骨细胞孔隙弹性本构模型的渗透率数值差异性及参数可靠性问题.关于软骨细胞本构模型的研究取得了一定程度的进展,但其力学响应与计算模型本构参数之间的高度复杂非线性使得软骨细胞的本构参数反求仍是一个具有挑战性的问题.

人工智能的飞速发展为其他学科领域提供了解决问题的新思路,能够高效模拟输入和输出变量之间的非线性相关性的机器学习方法逐步应用于生物力学领域[14-15].研究表明,利用可靠的正演模型来进行反演分析是系统识别材料性质的有效手段[16-17].李洋等[18]集成有限元与智能算法实现了骨骼肌本构参数的反演方法研究.Arbabi 等[19]基于人工神经网络和软骨孔隙弹性压痕有限元模型,确定了软骨的力学和物理性能.Wang 等[20]基于红细胞的光镊拉伸过程的有限元模型利用BP 神经网络实现了红细胞膜本构参数识别,探索了原子力显微镜压痕下红细胞的局部变形机理.然而,取决于参数组的维度以及生物代理模型的复杂度,如何在有限的实验及仿真成本下提高生物材料参数反演的效率和精度仍是值得探讨的问题.Liu[21]提出了一种用于正反向力学问题实时计算的双向深度网络TW-Deepnets (twoway deepnets)模型,该模型被证明可以在基于物理定律的小样本问题上取得更高的预测精度[22].同时,在有关中小型结构表格数据方面,决策树算法具有良好的预测效果,随机森林(random forest,RF)是一种基于决策树的回归技术.在计算生物学工作中,RF 已被证明在处理小样本量,高维特征空间和复杂数据结构方面具有独特的优势[23].

因此,本论文基于软骨细胞无侧限压缩实验有限元模型以及TW-Deepnets 模型、RF 模型,分别提出了两种反演方法,用于识别软骨细胞黏弹性本构参数.同时,结合数据采样对比和智能算法超参数优化过程,拟合Nguyen 等[24]的实验曲线来验证和对比所提出的反演方法的有效性,并通过使用统计指标R2对比了这两种方法对骨细胞本构参数的预测能力.

1 有限元建模

基于Nguyen 等[24]的实验,使用有限元软件ABAQUS(6.14)模拟了单个软骨细胞的无侧限压缩松弛实验,通过微操作技术在悬浮液中对分离出的单软骨细胞的机械响应进行了实验研究.因此,本论文中的骨细胞有限元模型没有考虑细胞与基质间的黏附效应.软骨细胞建模为一个直径为9 μm 的球形,该值是基于Nguyen 等[24]测定的牛软骨细胞的平均高度.如图1(a)所示,建立的有限元模型由刚性压缩板和球形细胞组成,考虑到几何形状和边界条件的对称性,采用了八分之一模型进行计算,由2420个线性六面体单元和11 139 个节点组成,单元类型采用C3D8R 单元.沿对称面施加对称边界条件,细胞和板之间定义无摩擦的面面接触.在有限元分析过程中建立了两个分析步: 第一个分析步为0.75 s,在这一分析步中,如图1(b)刚性压缩板匀速施加竖直向下的2.25 μm 的位移;第二个分析步为2.25 s,在这一分析步中,刚性压缩板位移保持不变,模拟软骨细胞应力松弛过程.

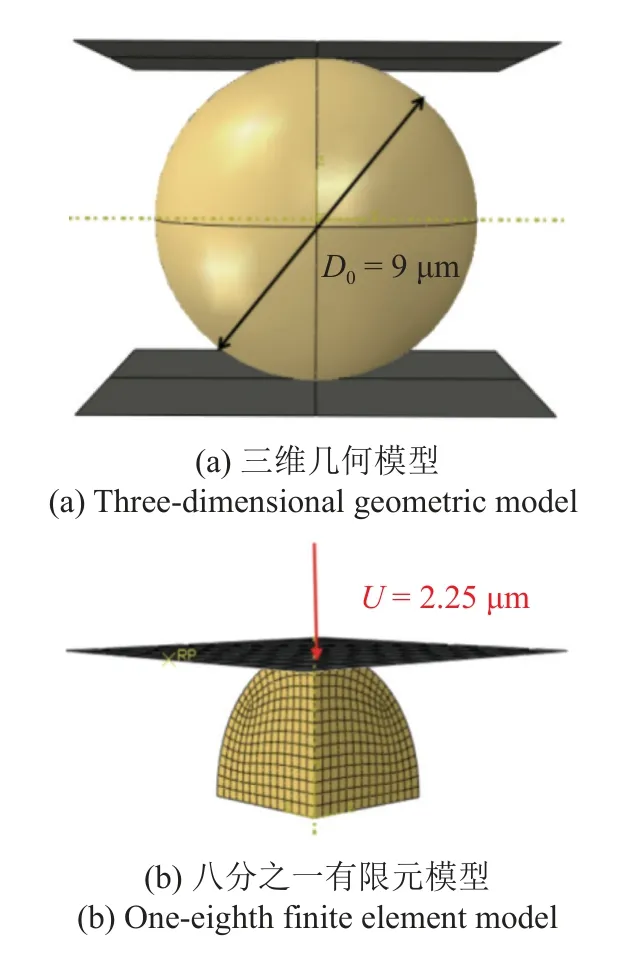
图1 软骨细胞压缩有限元模型Fig.1 Finite element model of chondrocyte compression

2 MSnHS 本构模型

黏弹性模型是细胞力学研究中最常用的力学模型之一[25].Nguyen 等[26]提出了一种修正的非线性黏弹性本构模型(MSnHS),解释了单细胞的应变率依赖行为,但研究只限于软骨细胞的压缩过程.本研究中,基于MSnHS 本构结合无侧限压缩实验的压缩及松弛过程来探究单个软骨细胞的时间依赖性全局力学性能,并分析细胞应力松弛机制对各本构参数的依赖性.软骨细胞的非线性、弹性力学响应采用可压缩Neo Hookean 超弹性模型,该模型的应变能密度表达式为

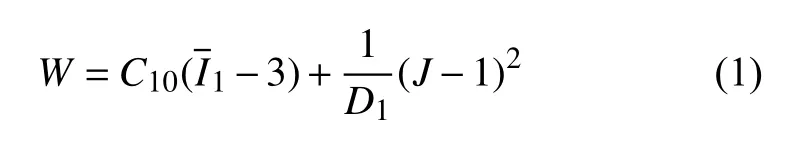
式中,C10为与剪切模量相关的本构模型参数;W为单位体积应变能;D1为材料的可压缩性;J为材料的体积比;为左柯西−格应变张量的第一应变不变量.

黏性模型的剪切松弛模量以及体积松弛模量的一项Prony 级数展开表达式为

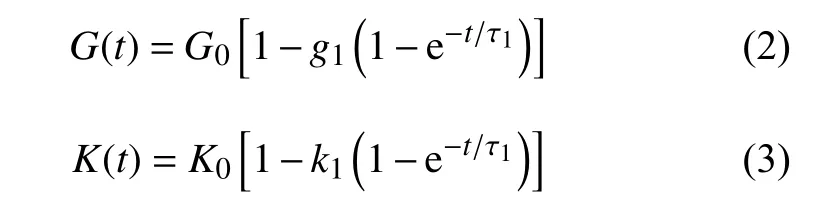
其中,G(t)和K(t)为剪切松弛模量和体积松弛模量;G0和K0为瞬时剪切模量体积模量;g1,k1,τ1为Prony 级数展开式的材料常数.将式(3)的黏性材料特性与式(1)描述的超弹性材料特性合并即为描述软骨细胞的MSnHS 本构模型.

3 双向深度神经网络与随机森林

双向深度神经网络模型,基于物理定律的模型,如有限元方法FEM,光滑FEM (S-FEM)和无网格模型进行训练,用于材料和结构的正、反力学问题的实时计算[21].有限元系统矩阵的良好特性,使得有限元−人工智能深度网络能够有效地训练正向力学问题,为高成本的反向传播提供了坚实的基础.在本论文中,基于有限元收集的数据,正问题神经网络建立了一个由材料参数预测软骨细胞压缩接触力随时间历程变化的代理模型,反问题神经网络则结合实验数据及正问题代理模型进行MSnHS 本构参数反求,利用双向深度神经网络进行软骨细胞参数反求问题流程图如图2 所示.

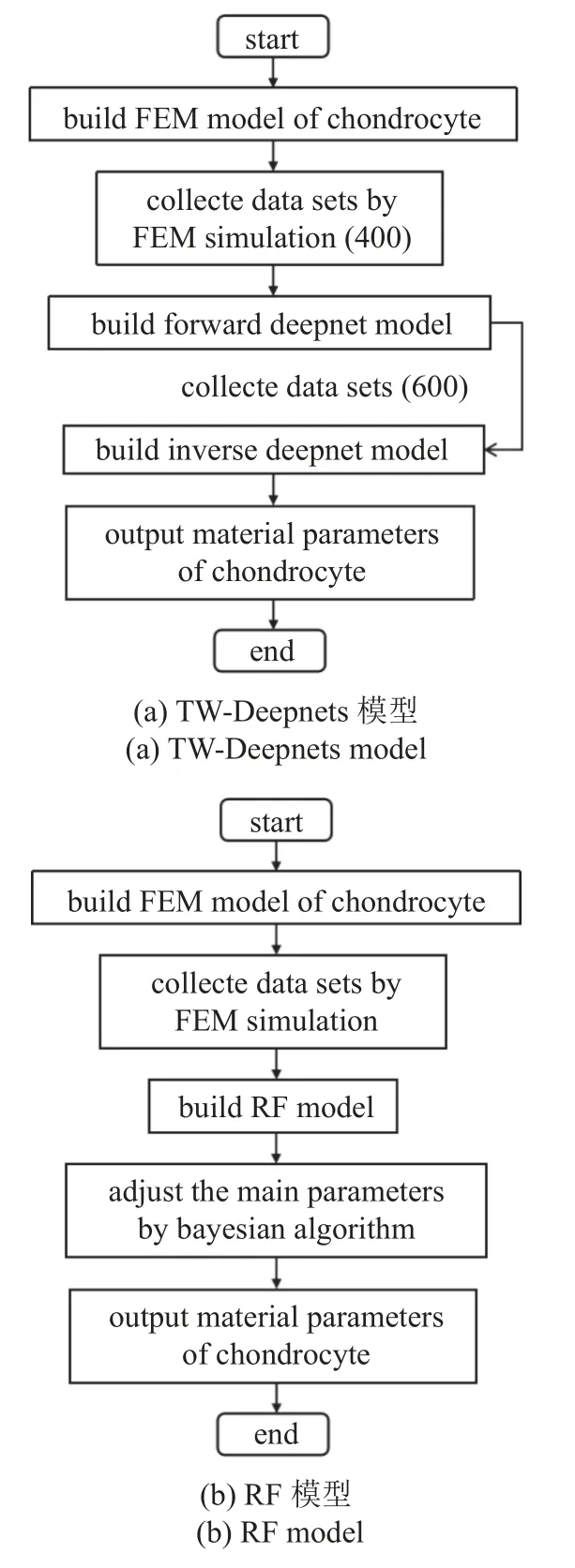
图2 本研究中提出的本构参数识别方法流程图Fig.2 The flow chart of the parameter identification method proposed in this study

随机森林是一种经典的Bagging 模型,其弱学习器为决策树模型,在回归问题上具有强大的非线性关系学习能力[27-28].RF 回归模型基于原始数据的随机抽样创建大量不相关的决策树,并根据每个决策树的平均值获取最终结果.如图3 所示,与其他算法不同,RF 回归模型将原始数据通过随机抽样分为两部分,即袋内训练数据和袋外验证数据OOB.使用OOB 数据而非外部数据用于评估学习性能,使得RF 模型具有更强的回归预测能力.利用随机森林进行软骨细胞参数反求问题流程图如图2(b)所示.

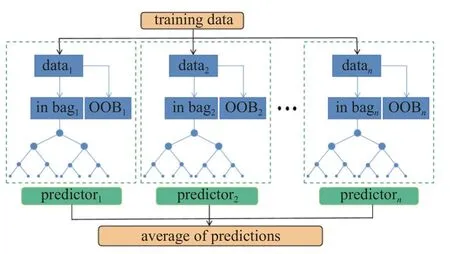
图3 随机森林模型预测结构示意图Fig.3 The structure of the RF model

4 预测结果与讨论

4.1 数据准备

MSnHS 本构参数空间的必要参数为五个,分别为C10(取值范围700～ 2630),D1(取值范围50～2260),g1(取值范围0.25～ 0.7),k1(取值范围0～ 1),τ1(取值范围0～ 1),参数范围的确定基于相关文献对软骨细胞本构模型的研究.研究表明,均匀采样和拉丁超立方采样(LHS)在采样空间的均匀性及空间填充性上具有各自的优势[29].本研究中,为了提高基于采样的分析效率、收敛性和鲁棒性,使用将均匀采样与LHS 结合的混合抽样方法,即在参数空间内分别采用LHS 及均匀抽样法各采集200 组材料参数继而合并得到采样量为400 的材料参数组.接下来,基于软骨细胞的有限元模型,获取材料参数与细胞和压板间的接触响应力的对应数据集,用于搭建能够反求本构参数的TW-Deepnets 模型及RF 模型.为了消除特征间的量级差异性,使得回归问题能够更加准确快速的收敛,本研究对数据进行标准化处理

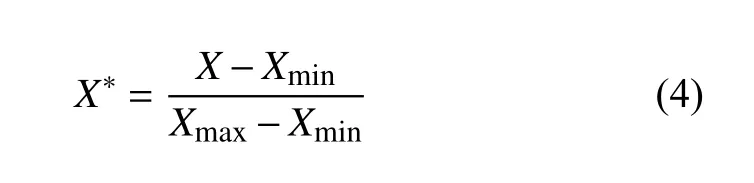
式中,X*为标准化后的值,X为原始值;Xmax,Xmin分别为特征数据范围内的最大值和最小值.

为了测试基于混合抽样法所得数据集的分析效率,基于均匀抽样法,拉丁超立方抽样法以及混合抽样法的数据集,对所搭建的软骨细胞神经网络代理模型的预测效果进行了对比.代理模型的输入为本构参数,输出接触力,以均方误差函数MSE为损失函数,表达式如式(5)所示

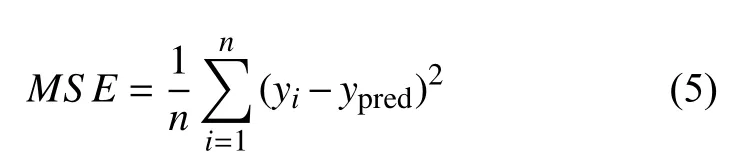
式中,n为样本量,ypred为预测值,yi为真实值.

如图4,基于混合采样数据的软骨细胞压缩实验神经网络代理模型的预测误差MSE明显小于基于其他两种单一采样方法数据的预测误差,说明本研究采用的混合采样法在数据驱动预测问题中的高效性.

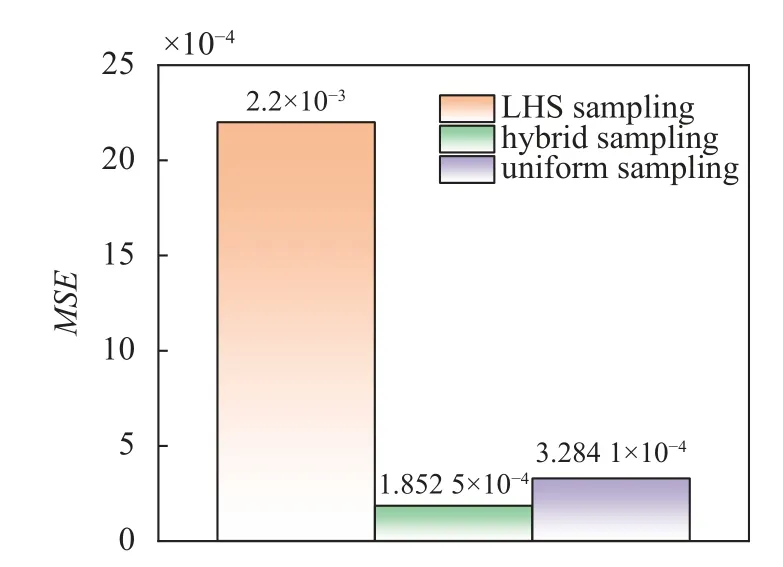
图4 软骨细胞代理模型的误差对比Fig.4 Comparing the MSE of neural network proxy model under different sampling methods

4.2 贝叶斯超参数优化

神经网络模型的主要超参数包括学习率、隐藏层数、隐藏单元数、激活函数,通常使用经验公式或交叉验证方法[30]对超参数进行估计.本文基于贝叶斯(Bayesian)优化构造了神经网络超参数搜索空间模型,用高斯过程填充样本点之间的区域,寻找验证集上均方误差函数MSE最小值的参数组合.神经网络最优超参数组搜索空间为: 学习率(10−6～10−1)、隐藏层数(1～ 10)、隐藏单元数(5～ 50)、激活函数(Relu/Sigomid).图5 为优化后双向神经网络的网络架构.同样使用贝叶斯优化对随机森林的重要超参数进行优化,随机森林主要模型参数包括决策树的数量、RF 最大深度、内部节点分裂所需的最小样本.表1 为Bayesian 优化后的TW-Deepnets模型及RF 模型超参数值.

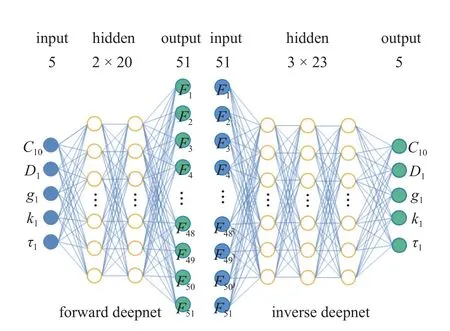
图5 TW-Deepnets 模型架构Fig.5 TW-Deepnets model architecture

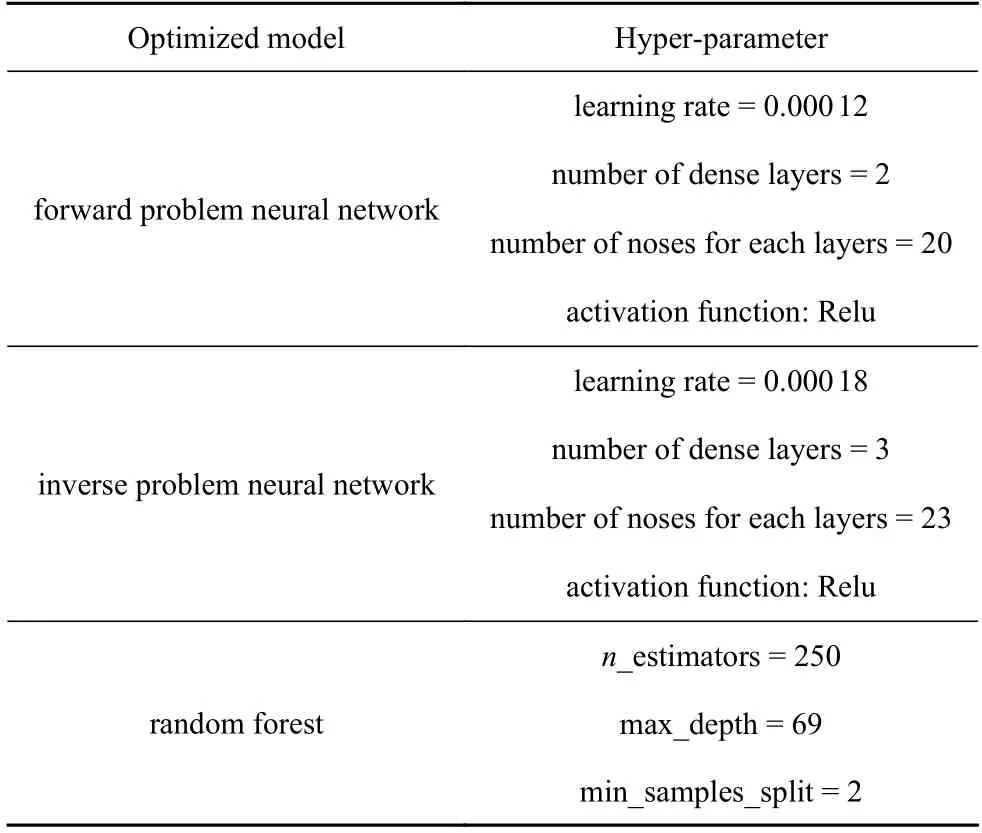
表1 Bayesian 优化算法确定的模型超参数Table 1 Hyperparameter values obtained by Bayesian optimization

4.3 参数预测结果分析

有限元收集到的初始样本量以7:3 的比例对训练集和测试集进行分配.TW-Deepnets 模型使用均方误差(MSE)作为损失函数,通过真实值与预测值的距离来指导模型的收敛方向.其中正问题神经网络在测试集上的MSE为2.076 2 × 10−6,反问题神经网络在测试集上的MSE为1.4 × 10−4,正反问题模型在测试集上的良好表现保证了模型的泛化能力及预测的准确性.对于随机森林模型的评估,采用均方根误差函数(RMSE)测量预测值与真实值之间的偏差,RF 模型在测试集上的RMSE为0.041,偏差程度较小.均方根误差函数公式为

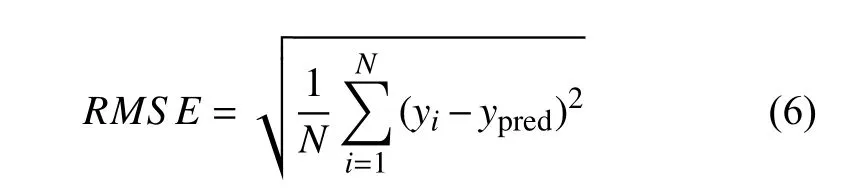
式中,N为样本量,ypred为预测值,yi为真实值.

为了更好地对比两种模型对软骨细胞本构参数的预测能力,通过决定系数R-square(R2)来评估参数C10,D1,g1,k1,τ1真实值与预测值的拟合程度.R2利用数据的平均值作为误差基准,观察预测误差的偏离程度.R2定义为

式中,yi为真实值,ypred为预测值,y为真实值的平均值.

图6 为TW-Deepnets 模型和RF 模型对10 组参数预测的R2结果对比,两种模型预测所得各个参数均能达到较高的拟合优度(R2均值 >0.80),而TW-Deepnets 模型总体情况好于RF 模型.可以观察到C10,g1的预测效果拟合优度总是很高(R2>0.9),而D1,k1,τ1的拟合优度会低一些,这说明在利用软骨细胞压缩实验挖掘其全局力学性能与MSnHS 材料参数复杂的非线性关系中,C10,g1起重要影响,而τ1,k1的影响占比较小,D1最小,这与文献[9]的研究结论一致.图7 为RF 由参数预测压缩力时的Scikitlearn 特征重要性,代表各个特征对于预测力的贡献大小,即更加直观地验证了MSnHS 本构各参数对描述软骨细胞时间依赖性力学行为的影响占比.

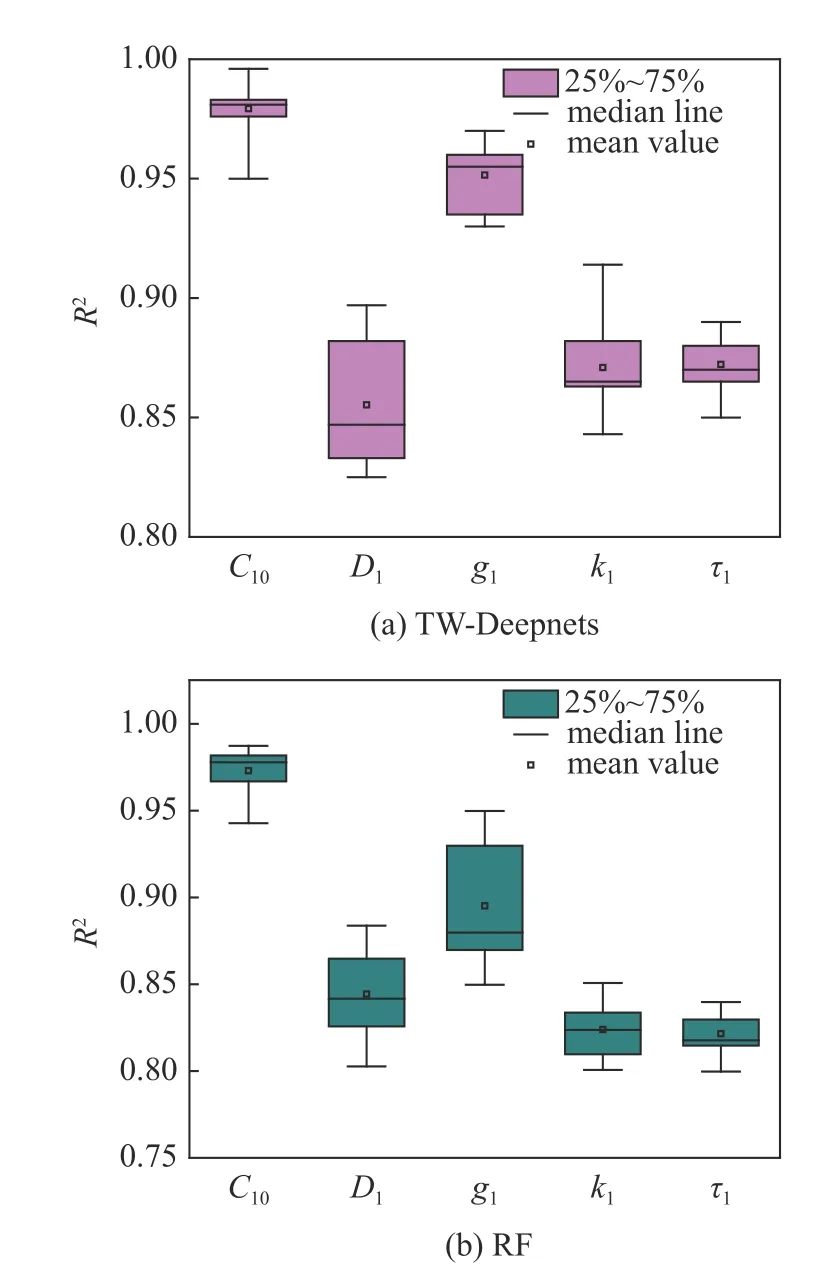
图6 本构参数预测性能检验Fig.6 Test of constitutive parameters prediction

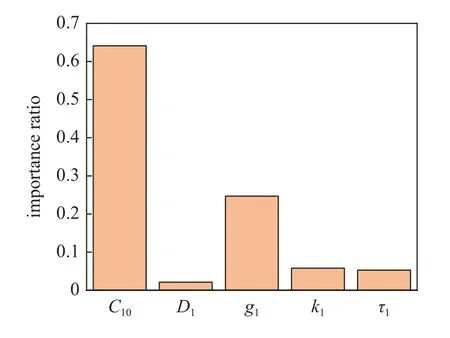
图7 MSnHS 本构参数特征重要性占比Fig.7 Importance ratio of MSnHS constitutive parameters

利用文献[24]中0～3 s 内单个软骨细胞受到50%压缩程度下与压缩板间的实验接触力数据,TWDeepnets 模型和RF 模型各预测得到一组MSnHS本构参数值.表2 为两个参数反求模型的本构参数预测结果.将预测所得的本构参数输入有限元模型,对比有限元响应曲线与实验曲线的拟合程度来验证预测所得参数的可靠性.图8(a)为分别基于两个参数反求模型预测所得有限元模型响应曲线与实验曲线对比.其中,由TW-Deepnets 模型预测所得的MSnHS 有限元响应可以很好地和实验曲线拟合(R2=0.987),RF 模型的预测响应在压缩阶段可以与实验曲线很好地拟合,而应力松弛阶段存在轻微的滞后现象,需要达到最终松弛状态的时间更长,压缩反作用力更小,与实验曲线的拟合程度为R2=0.912.因此,本文提出的集成有限元模型和TW-Deepnets模型以及集成有限元模型和RF 模型进行参数反求的过程都是预测软骨细胞的MSnHS 本构参数的有效方法,其中TW-Deepnets 模型表现出更高的准确度.

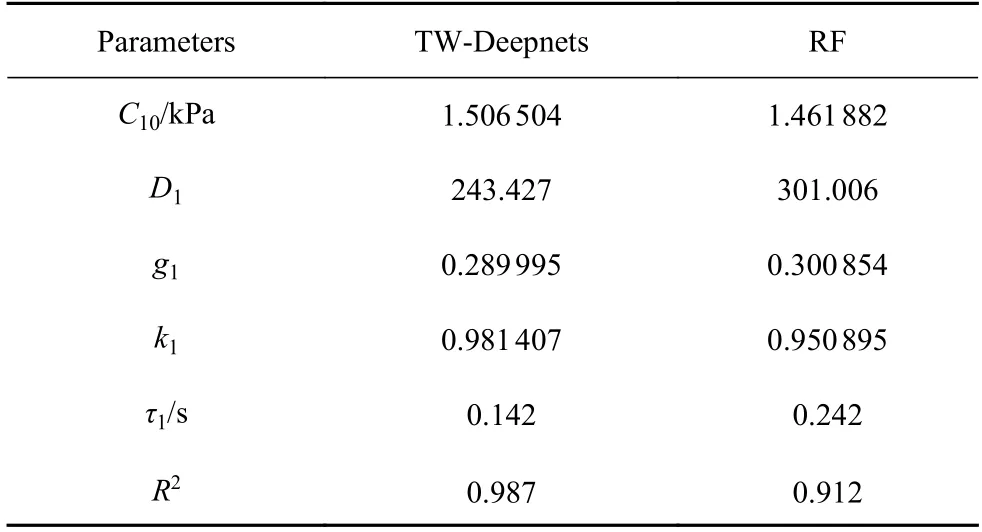
表2 MSnHS 本构模型参数预测结果Table 2 Parameters prediction results of MSnHS

将本文中利用TW-Deepnets 模型预测所得的软骨细胞压缩有限元响应与文献[13]利用传统反有限元方法进行参数预测所得的软骨细胞压缩力学响应曲线进行对比.从图8(b)中可以直观看出,无论是基于黏弹性本构模型还是基于孔隙黏弹性本构模型,传统反有限元方法预测所得的响应力最大值点都存在较大偏差,并且基于黏弹性本构的预测模型对于细胞松弛过程中响应力松弛速率与实验存在一定差异.这说明,相较于传统的反有限元方法,基于TWDeepnets 模型的参数反演方法能够预测更加可靠的软骨细胞本构参数,从而能够建立更加准确的计算模型进行力学性能研究.同时,MSnHS 本构模型也被证明能够很好地对软骨细胞的时间依赖性全局力学性能进行描述.

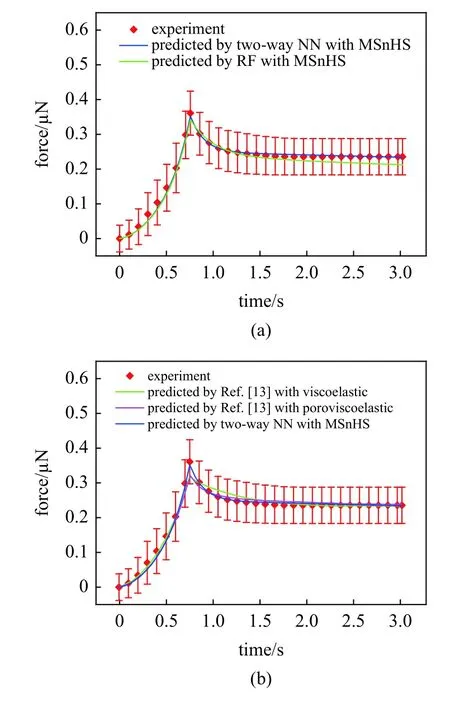
图8 模型预测与实验的时间−力曲线对比Fig.8 Model predictions are compared with experimental time-force curves

软骨细胞通常表现出应变率依赖性行为,其力学响应也与加载速率有关,如图9 为软骨细胞有限元模型在不同压缩加载速率下的力响应曲线,压缩速度越快,最终变形时细胞与压板间的接触力越大.然而在细胞松弛后,即在细胞保持数秒后,所有力都达到相同的平衡力,这与Nguyen 等[24]的实验结论一致,表明本研究中的软骨细胞本构关系及有限元模型能够捕捉单软骨细胞的应变率依赖性行为.图10 为软骨细胞受到50%压缩后3 s 应力松弛前后的Mises 应力云图(单位为MPa).正如松弛前的应力云图所示,软骨细胞受到压缩后的最大应力值点集中在细胞的中心,应力值由中心向外围不断减小.随着松弛时间的增加,细胞整体应力值逐渐减小,在3 s 后达到最终状态,此时应力最大处的应力值减少了4.969 kPa.

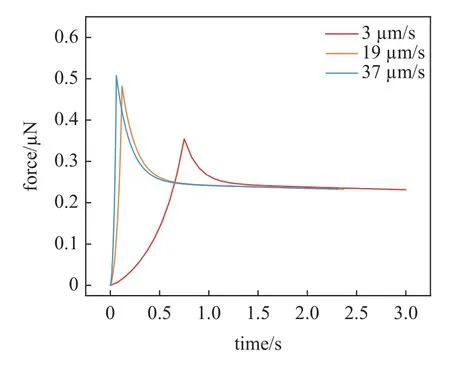
图9 软骨细胞不同压缩速度下的时间−力曲线Fig.9 Time-force curves of chondrocytes at different compression rates

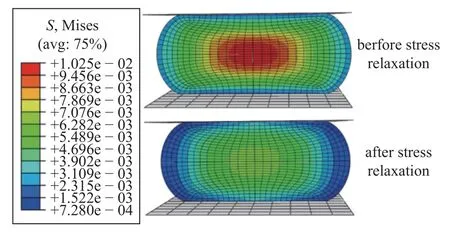
图10 软骨细胞3 s 应力松弛前后Mise 应力云图Fig.10 Mises stress cloud diagram of chondrocytes before and after 3 s stress relaxation

5 结论

本论文提出了分别利用TW-Deepnets 模型和RF 模型结合有限元系统来识别软骨细胞的MSnHS本构参数的反演方法.建立了软骨细胞的无侧限压缩有限元模型用于数据收集,利用决定系数R2对两种模型对各参数的预测性能进行了对比评估,分析了参数特征重要性占比.最后,利用文献[24]的实验曲线验证了反演方法的有效性,得出如下结论.

(1) 基于建立的软骨细胞无侧限压缩实验有限元模型,结合数据采样对比和超参数优化,利用TWDeepnets 模型和RF 模型确定了能够描述单个软骨细胞时间依赖性力学特性的本构参数取值,预测所得有限元响应与实验曲线吻合良好.

(2) MSnHS 本构模型能够很好地描述包括压缩过程和后续的应力松弛过程中软骨细胞的时间依赖性力学性能.其中,利用软骨细胞无侧限压缩实验挖掘其全局力学性能与MSnHS 材料参数复杂的非线性关系中,C10,g1起重要影响,而τ1,k1的影响占比较小,D1最小.

(3) TW-Deepnets 模型和RF 模型对于预测软骨细胞黏弹性本构参数都具有很大的潜力,就本研究来说,TW-Deepnets 模型表现出更高的准确度和稳定性.该方法也可进一步推广到其他维度更复杂的本构参数反求及其他类型细胞在负载下更复杂的细胞微观力学现象.