连接组合结构协同动力学拓扑优化设计1)

文明 王栋

(西北工业大学航空学院,西安 710072)

引言

拓扑优化的目的是在给定的设计区域内,寻求结构最佳的材料分布与传力路径,使结构的力学性能及响应指标在设定的静、动力载荷作用下达到最优[1-4].当结构的初始构型设计无法借助于设计者以往的经验确定时,拓扑优化能够在给定的载荷和一定的约束条件下搜寻出创新性的结构构型设计,充分发挥材料性能潜力,进而显著提高工程设计的效率和质量[5-8].因此,拓扑优化设计是目前工程设计领域非常重视的课题.然而传统的与结构拓扑或形状相关的优化设计问题通常只是对单个承力构件或部件进行的[9-12].

实际工程结构,如火箭、卫星、太阳能帆板等结构,都是由许多零部件,通过各种方式连接组合而成[13-17].而结构的各部件(或子结构)之间,以及结构与周围基础环境的连接状况,如连接形式、位置、约束性能等,都会对结构的整体性能产生很大的影响,因而也是结构完整性设计不可或缺的重要组成部分[18-20].连接构件将各承力构件紧密联系在一起,使其能够很好地发挥各自的作用.连接构件的约束状况及性能,对各部件之间载荷或振动能量的传递方式与路径,都有非常重要的影响,进而又影响整个结构的静、动态特性及其对外载荷的响应.仅仅追求结构中某个局部件性能的最优,并不能使系统整体性能达到最优,而组合结构的整体最佳性能需要各组成部分特性的相互匹配与协调.对于组合结构的拓扑优化设计,不同的连接构件布局及约束性能对应着完全不同的最优材料分布.若仅对单一承力构件进行优化设计,忽略了连接约束对传力路径的影响,则所得到的拓扑构型将无法有效地传递外载荷和振动能量.因此在结构拓扑优化中应将连接约束与承力构件作为一个整体进行设计,在优化承力构件拓扑构型的同时优化连接构件的布局设计,以便获得连接组合结构整体意义上的最优材料布局.

目前已有相关学者对连接约束的型式、数量、位置和刚度与结构整体性能之间的关系做了一些分析和设计优化研究.Zhu 等[21]在对结构的拓扑进行优化时,将连接构件传递的载荷也作为一种约束条件.优化结果表明,只有当连接约束性能分布均衡时,组合结构内的应力水平才能得到有效控制.乔赫廷等[22]研究了结构的构型与连接方式协同静力学优化设计问题.结果表明结构的拓扑构型设计与连接构件的布局密切相关,两者协同优化设计对改善结构的内力分布至关重要.马振云等[23]研究了连接刚度和位置变化对外力传递性能的影响.通过调整连接构件的约束刚度和位置,可使传递的载荷在各连接构件上得到均衡配置,并导致结构内的应力水平趋于均匀.田瑞等[24]研究了梁结构支承约束反力的均衡设计问题.通过调整支承连接构件的约束刚度,可使梁结构各支承反力达到一致或按刚度大小分配,从而避免了某些连接构件由于约束力过大而提前破坏或失效等问题.当前人们对连接约束条件的分析与优化设计,主要集中于改善连接约束构件载荷分布或连接组合结构的静力学性能.对连接组合结构的拓扑优化设计,并通过改变连接约束构件的分布以改善结构的整体动力学性能,降低组合结构动响应的研究还相对较少.

本文开展具有连接约束构件的组合结构协同动力学拓扑优化设计研究.首先以弹簧连接单元模拟工程中承力构件之间的连接约束与承载状况[25],基于材料属性的有理近似方法(rational approximation of material properties,RAMP)[26],建立了连续体结构在简谐激励作用下的协同拓扑优化模型.随后以组合结构整体动柔顺度最小(即动刚度最大)为设计目标[27],以承力构件材料用量和弹簧连接单元数量为约束条件,采用移动渐近法(method of moving asymptotes,MMA)[28],对整个结构的拓扑构型与弹簧连接单元布局进行协同优化设计.最后通过两个典型算例验证了本文所提协同动力学优化模型的有效性和优化算法的可行性,并与传统的单体式结构优化结果进行对比,充分展示了连接约束构件的存在与布局设计对组合结构材料分布以及动力性能的影响.

1 连接组合结构协同拓扑优化模型

1.1 线性系统稳态振动响应

首先采用有限元法对连续体结构进行离散化处理,则系统受迫振动的运动方程为

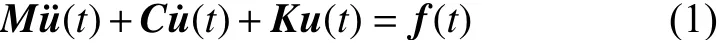
式中,K,M,C分别是N × N阶的结构刚度、质量和阻尼矩阵,N表示结构的自由度数.u(t)和f(t)均为N维列阵,分别表示结构的位移响应与外激励.假设结构受到简谐外激励的作用

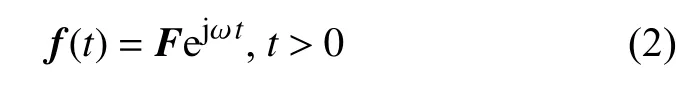
其中,F是外激励幅值N维列阵.ω是外激励圆频率(弧度/秒).在简谐载荷的作用下,线性系统的稳态响应也是同一频率的简谐运动

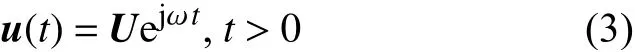
式中,U是结构位移响应幅值列阵.由于要考虑结构内的阻尼,U是复数.将式(2)和式(3)代入振动方程(1),消去时间项,得到频域内振动系统响应的特征方程

式中,Kd=K−ω2M+jωC是系统的动刚度矩阵,是激振频率的函数.求解方程(4)可得结构响应的幅值列阵U,进而由式(3)可以得到时域内结构的动响应u(t).

1.2 拓扑问题描述与协同优化模型

假设一个组合结构由两个承力构件组成,如图1所示,连接构件将构件1 的节点i与构件2 的节点j紧密联系在一起.以弹簧连接单元模拟连接构件在i与j两节点之间的约束作用,该连接单元由能够同时约束相对拉伸变形和剪切变形的复合弹簧组成.于是,连接单元的节点位移列阵可表示为

图1 连接约束力学模型Fig.1 Mechanical model of a linkage member

假设传递拉伸力的刚度系数为kt,传递剪切力的刚度系数为ks.剪切约束刚度与拉伸约束刚度相互独立,彼此间没有耦合效应,也不考虑连接约束弹簧的质量和阻尼.则弹簧连接单元的等效刚度矩阵可表示为

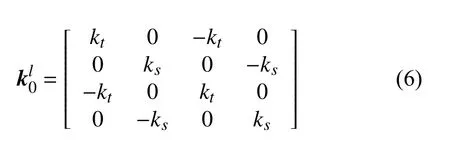
为了求解组合结构的拓扑优化问题,首先需建立结构的协同优化数学模型.与以往不同的是,此时结构的设计域是不连通的,各承力构件仅通过连接构件相互耦合,且连接构件的最优位置分布亦将采用拓扑优化的方式确定.以结构动柔顺度Cd(动刚度的倒数)最小为设计目标,以承力结构材料体积与弹簧连接单元数量作为约束条件,其拓扑优化列式为

式中,τ是拓扑设计变量列阵,其中ρi表示承力构件中单元的相对密度,ηi表示弹簧连接单元的相对刚度,NE代表承力构件的单元总数,n代表弹簧连接单元的总数.V是优化后承力结构的体积,fv是承力构件区域的总体分比,则fvV0即为优化结束后剩余的承力构件材料体积上限值.Πmax代表弹簧连接单元的数量上限值.ηmin是弹簧连接单元相对刚度ηi的下限,ρmin是承力构件单元的相对密度ρi的下限,采用它们是为了避免结构刚度矩阵出现奇异性,本文取ηmin=ρmin=0.001.通过承力构件中单元的相对密度和弹簧连接单元相对刚度来描述承力构件的拓扑构型与连接构件的布局.

本文以变密度法中有理近似材料(RAMP)模型统一对承力构件的单元刚度矩阵和弹簧连接单元的刚度矩阵进行插值[25]

2 灵敏度分析

假设外激励不依赖于结构的拓扑设计变量.由动柔顺度的定义式(8),其对承力构件每个单元设计变量的一阶导数可由如下公式计算[9]

式中,(FTU)*是(FTU)的共轭复数,Re(·)表示对括号里的值取实部.可见结构动柔顺度对设计变量的一阶导数归结为结构的结点位移对设计变量的一阶导数.由方程(4)两侧同时对设计变量ρi求导,经过移项后可得

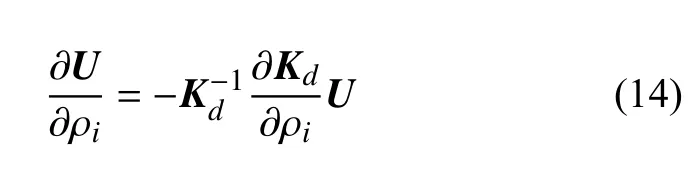
将式(14) 代入式(13) 可得结构的动柔顺度Cd对承力构件单元拓扑变量的一阶导数表达式

此外,还要在各承力构件区域内运用启发式灵敏度过滤技术[29],对动柔顺度灵敏度分别进行再分配处理,以避免各构件相互之间的干扰并消除优化过程中的棋盘格现象,保证优化结果的数值稳定性.

3 算例分析

本节用两个二维平板结构算例验证本文所提方法的可行性,展示连接组合结构协同优化效果、结构的拓扑构型与弹簧连接单元分布规律.假设板的厚度均是10 mm,材料的弹性模量E=200 GPa,泊松比0.3,密度7800 kg/m3.仅考虑承力结构的阻尼,采用比例阻尼模型:C=αMp+βKp,其中α=150,β=10−5,Mp和Kp分别是平板结构的质量和刚度矩阵.弹簧连接单元的拉伸刚度系数kt与剪切刚度系数ks均为500 MN/m,简谐激励幅值F=10 kN.优化过滤半径为单元尺寸的1.5 倍,优化过程收敛条件设置为相邻两次迭代各设计变量的最大改变量小于0.01.

3.1 双板弹簧连接结构

图2 所示的双板组合结构,左侧边界固支,在两板之间要求最多设置4 个连接约束构件.将两个承力板分别划分成 50 × 50 的四结点平面应力单元网格,材料体分比fv=0.35.初始设计时弹簧连接单元布满整个连接区域,共有51 个连接构件位于承力构件的相关节点之间.初始设计变量均给定为0.35.简谐激励频率ω/(2π)=100 Hz.

图2 双板弹簧连接组合结构Fig.2 A combined structure of two panels with spring linkage members

图3(a)示出了按照以上介绍的协同拓扑优化方法得到的连接组合结构构型设计,其中黑色水平线表示弹簧连接单元的最优位置.弹簧连接单元分别位于上下两侧,其中上侧两个连接单元之间有3 个单元尺寸的间隔距离,而下侧的两个连接单元平行相连(即分别位于同一组承力单元的上下节点处).由于两个承力构件间只在上下处连接,因此外侧承力构件先将外载荷分别传至上下弹簧连接处,通过连接构件传递到内侧承力构件,然后再传至固支边界上.内侧构件的材料分布上下基本对称,而外侧构件的构型可以视为是由两个稳固的三角形构件组成.

图3 连接组合结构拓扑优化构型对比Fig.3 Comparison of topology configurations between the combined structure and the integral one

图4 绘出了协同优化设计的动柔顺度和弹簧连接单元数量的迭代收敛过程.初始设计时,弹簧连接单元的数量并不满足约束条件(0.35 × 51=17.85 >4).随着优化过程的持续,连接单元的数量约束很快就得到满足,而且目标设计函数也稳步地收敛到最小值.

图4 协同优化设计目标函数与约束函数迭代过程Fig.4 Iterative histories of the design objective and linkage member number of the collaborative topology optimization

作为对比,若人为地将4 个弹簧连接单元平行分布于承力构件上下缘最外侧单元的两组节点之间.这时只对承力构件的拓扑构型进行优化设计,所得结果如图3(b)所示.此时组合结构的拓扑构型与图3(a)基本相同,只是由于上侧的两个弹簧连接单元平行相连,使外侧构件的斜撑杆上端也向上移动了一定的距离.从而使外侧承力构件连接处没了那一段连接平台,如图中的蓝圈所示,导致结构的动柔顺度也会有一定的改变.

而传统的单体式结构拓扑优化所得构型如图3(c)所示.此时的材料布局相对更简洁一些,外力传递到固定边界更加直接.特别是垂直外激励的一部分将沿着上缘构件直接传递到固定边界上,不会出现传递分散的现象.虽然单体结构的框架式构型也会通过上下连接构件所在的位置,但外侧区域构型仅有一个三角形.即若从单体结构的拓扑优化构型图3(c)出发,在指定的位置用连接构件替换原来的材料,却无法获得组合结构协同优化的拓扑构型.

表1 列出了以上三种情形的结构拓扑优化数值结果.可以发现组合结构的动柔顺度均大于单体式结构的相应值,即连接组合结构的动刚度略小一点.这首先是由于组合结构构型变化所致,导致组合结构对简谐激励的动响应有所增大.其次,由于连接弹簧的数量较少,连接构件的使用断开了沿上下缘分布的主承力结构件,不可避免地削弱了结构的局部刚度,使组合结构的整体刚度有一些损失.

表1 拓扑优化结构的动柔顺度以及前二阶固有频率对比Table 1 Comparison of the optimal dynamic compliance and the first two natural frequencies

由表1 还可以发现,人为布置连接构件所得到的组合结构动柔顺度相比于协同优化设计所得结果要稍大一些(增加了5.7%).由此可知: 虽然两者的拓扑构型基本一致,但组合结构的协同优化构型设计整体动刚度更大.这充分体现了连接组合结构拓扑构型与连接构件布局的协同优化设计的益处,同时也表明了连接构件的布局设计对结构整体性能会有一定的影响.

作为进一步的研究,若将连接弹簧单元数量上限增至8 个,其余参数均保持不变.则协同拓扑优化后结构的构型设计相比于4 个弹簧连接单元时所得的构型基本一致,见图5 所示.弹簧连接单元最优布局为下侧连续分布4 个弹簧连接单元,上侧靠内部的一个弹簧连接单元与外部连续分布的三个弹簧连接单元相隔两个单元的距离.虽然组合结构的动柔顺度较只有4 个弹簧连接单元所得构型的动柔顺度有所减小(5.143 5 J),但仍然大于单体结构的动柔顺度,这也从另一个方面表明组合结构的构型变化对其整体刚度的影响更大一些.

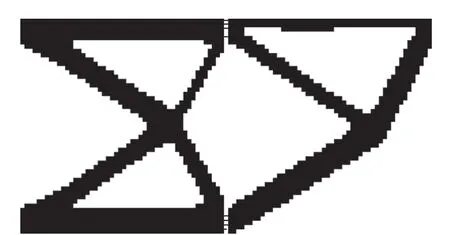
图5 连接组合结构拓扑优化构型(8 弹簧连接单元)Fig.5 Configuration of the combined structure of two panels with eight spring linkage members

深入研究发现连接组合结构的前二阶固有频率均比单体式结构相应的固有频率要大一些,如表1所示,而且协同优化构型设计的第一阶固有频率最大.图6 分别示出了两种结构的前二阶固有振型.可以看到,单体式结构的前二阶固有振型主要是上缘水平杆件的局部弯曲变形[30].而协同优化所得组合结构的第一阶固有振型是结构的整体变形.第二阶固有振型虽也是局部变形,但主要发生在结构外侧构件的三角支撑区域,其局部刚度明显比单体式结构的上缘水平构件更大.这就导致了连接组合结构的前二阶固有频率,明显大于单体结构固有频率的现象出现.由此可见,在连接组合结构的动力学拓扑优化过程中考虑连接构件的存在,由于所得构型的不同,对提高结构的振动特性也会有一定的帮助作用.

图6 结构前二阶固有振型对比Fig.6 Comparison of the first two natural modes between the combined and integral structures

3.2 固支深梁连接结构

图7 所示的组合深梁结构,左、右两端固定.假设在各承力构件之间均设置4 个弹性连接构件,但其位置暂时无法确定.分别将每一段梁划分成50 ×30 的网格.加载点位于组合结构的中心处,激励频率ω/(2π)=200 Hz.材料体分比fv=0.4.

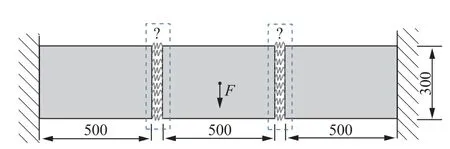
图7 连接组合深梁结构Fig.7 Combined deep beam with spring linkage members

组合深梁结构拓扑构型与连接约束单元布局的协同优化结果如图8(a)所示.同时,图8(b)示出了各将4 个弹簧连接单元分别布置于靠近上、下缘单元的两组节点处得到的组合结构拓扑优化构型.作为对比,传统单体式结构拓扑优化构型设计如图8(c)所示

图8 连接组合结构与单体结构拓扑优化构型对比Fig.8 Comparison of topology configurations between the combined deep beam structure and integral one

可以看到三种情形下所得结构的拓扑构型优化结果各不相同.协同优化所得组合深梁结构的构型(图8(a))与单体式结构的材料分布(图8(c))较为相似,外激励先通过中间的X 形构件传递到外框,然后再通过斜的外框传递到固定边界.外框较粗为主要承力结构件,中部形成了一个稳定的六边形构型.但协同优化设计将弹簧连接单元置于主承力构件上,使得中部连续的六边形出现断开现象.从而导致其中部X 形状承力构件相比于单体式结构中部的X 承力构件尺寸更大,且各传力路径之间保持相互正交[3].

而指定连接构件位置所得到的组合深梁结构拓扑构型(图8(b)),由于弹簧连接单元位于梁的上、下外侧,使得中间承力构件形成了比较复杂的传力路径.框架式构件组合体将外激励先传递到连接约束处,再通过斜外框传递到结构的固定边界.

表2 列出了三种情形结构拓扑优化数值结果.与前例一样,单体式结构的动柔顺度最小.连接组合结构的动柔顺度Cd比单体结构的优化结果分别大了12.4%和19.4%,而且人为布置连接构件所得拓扑构型的动柔顺度增加较多.表明组合结构拓扑构型与连接约束布局协同优化设计能更有效地抵抗外激励的作用,避免了人为布置连接构件位置对连接组合结构整体刚度可能造成的损失.

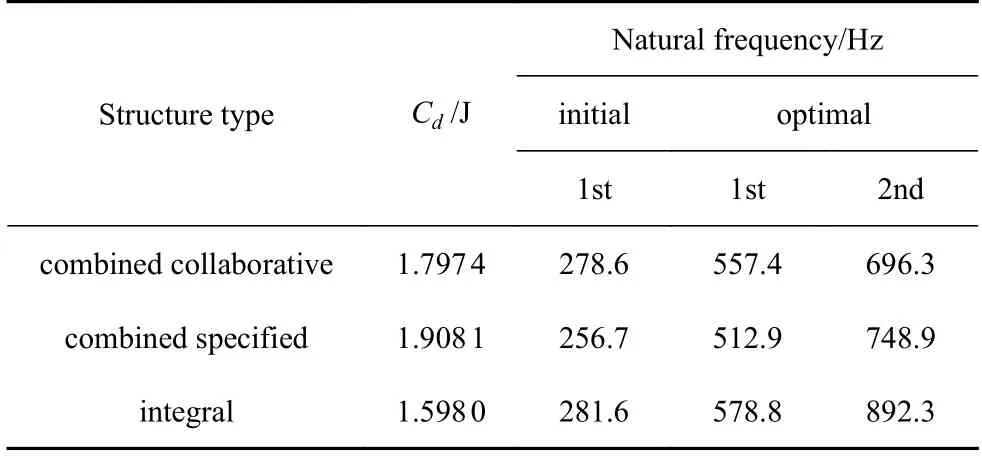
表2 拓扑优化结构的动柔顺度以及前二阶固有频率对比Table 2 Comparison of the optimal dynamic compliance and the first two natural frequencies

与前例不同的是,经过拓扑优化后,虽然三种构型的第一阶固有频率都有了很大的提高,使得外激励频率远离结构的共振区.但连接组合结构的前二阶固有频率均明显小于单体式深梁结构的结果,这显然是结构拓扑构型变化所致.因为优化后所得构型的前二阶振型均为整体变形,单体式结构比连接组合结构的动刚度更大,最终使得连接组合结构的前二阶固有频率低于单体结构的相应值.

图9 分别示出了拓扑优化后结构振动的变形幅值图.可以看到三种结构的最大位移响应均出现在外激励作用点处.协同拓扑优化所得构型与单体式拓扑优化所得构型的变形类似,而指定了连接构件位置的组合结构的中间段弯曲变形比较显著,这与中部承力结构件比较纤细有一定的关系.相反,协同优化组合结构与单体式结构均没有非常明显的变形段.

图9 连接组合结构与单体式结构动态变形对比Fig.9 Comparison of the structural dynamic deformations between the combined and integral deep beams

4 结论

本文研究了连接组合结构协同动力学拓扑优化问题,在设计承力构件拓扑构型的同时,也确定了连接构件的最优布局.以弹簧连接单元模拟工程结构中的连接约束构件,建立了分别以承力构件材料体积和弹簧连接单元数量为约束,在简谐激励作用下以连接组合结构动柔顺度最小为目标的拓扑优化模型.利用两个典型平面结构动态拓扑优化设计算例,验证了所提优化模型的有效性和优化算法的可行性.分析了连接约束构件的存在及其布局设计对结构优化构型设计的影响,并比较了两种结构的优化数值结果.研究结果如下.

(1) 连接约束的存在对优化结构的构型以及传力路径有较大的影响.由于承力构件之间仅靠连接约束构件连接,施加的外激励必须通过连接约束构件才能最终传递至结构的固定边界.

(2) 在相同承力构件体积约束的情况下,不论是最优连接构件布局对应的拓扑构型还是指定连接构件位置对应的构型,连接组合结构的动柔顺度总是大于相应单体式结构拓扑优化结果.这是由于原本连续的设计域被人为断开导致结构的整体刚度有所下降.而增大连接约束的刚度或数量,对提高结构的性能会有一定的弥补效果.

(3) 在相同连接构件数量约束的情况下,连接组合结构协同优化设计所得的动柔顺度总是小于人为布置连接构件所得结果.充分说明连接构件位置设计对结构构型的影响,最优的连接构件位置设计使结构抵御外激励的能力更强,所得结构的响应会进一步降低.体现了协同动力学优化设计独特的优点.

(4) 连接约束构件的存在,在改变优化结构构型的同时,也会改变结构的固有振型.合理的连接约束布局,能避免结构局部模态的出现,从而显著提高结构的动力特性,亦为后续组合结构的详细设计过程提供了更加优异的构型设计参考.