用GeoGebra教学频率分布直方图
2022-12-17莫竞
莫 竞
(东莞市第二高级中学,广东 东莞 523129)
0 引言
大数据时代的计算机技术不断提升,各种软件和现代信息技术在统计工作广泛应用,大大提高了统计工作的效率。数据分析是大数据时代数学应用的主要方法。《普通高中数学课程标准(2017年版2020年修订)》(以下简称《标准》)中建议,统计的核心是数据分析,统计的教学活动应通过典型案例进行,鼓励学生尽可能运用计算机处理数据[1]。根据《标准》的教学建议,学生需要通过处理案例获得数据分析的经验,习得数据分析的方法,理解数据分析的思路,从而能够区别统计思维与确定性思维、归纳推断与演绎证明的差异。可见,在统计内容的教学中,不仅要教授必要的统计技术,更重要的是要培养学生的统计思维。教学中教师应该充分发挥信息技术优势,剪枝节(统计技术),强主干(统计思维)[2]。
以频率分布直方图为例,它是普通高中数学必修内容。虽然绘制频率分布直方图仅有五个作图步骤,但是每个步骤的工作量都非常大,如果不借助于信息技术,学生将会在烦琐的数据操作中磨灭学习的热情,那就谈不上统计思维的培养了。于是,在信息技术支持下如何开展频率分布直方图的教学就成了必须逾越的课题。
通过软件例如Excel、SPSS等只要录入数据就能快速生成频率分布直方图,但这不利于学生理解频率分布直方图的构造和特点,例如很多学生经常会把纵轴的意义搞错[3],所以学生很有必要经历频率分布直方图的制作过程。经过探索,我们发现GeoGebra可用于频率分布直方图的教学。
1 GeoGebra的统计功能介绍
GeoGebra是一款能多平台使用的开源动态数学软件,因适用于几何学、三角学与微积分的动态图形而闻名。其实,该软件还有强大的统计分析功能。学生可以使用GeoGebra创建统计图,进行假设检验,并对现实世界的现象进行统计模拟,而且操作十分简便[4]。本文就利用GeoGebra教学频率分布直方图进行介绍。
GeoGebra自带统计功能包括:单变量分析、双变量回归分析、多变量分析、分布与检验等。例如,把数据输入表格区的A列后,选中A列再点击“单变量分析”的按钮,就能快速输出频数分布直方图,如果点击“显示统计”按钮,还能得到样本容量、均值、方差、标准差等基本的数据信息,拖动直方图上方的滑动条时,还能得到不同组数的图形。点开选项,我们可以选择“频数类型”中的“正态化”,就能得到“频率分布直方图”,如果选择显示“频数表”和“频数折线图”,就会在直方图上附加折线图,在直方图下方有“区间分组”和“频率/组距”的对应列表,如图1所示。
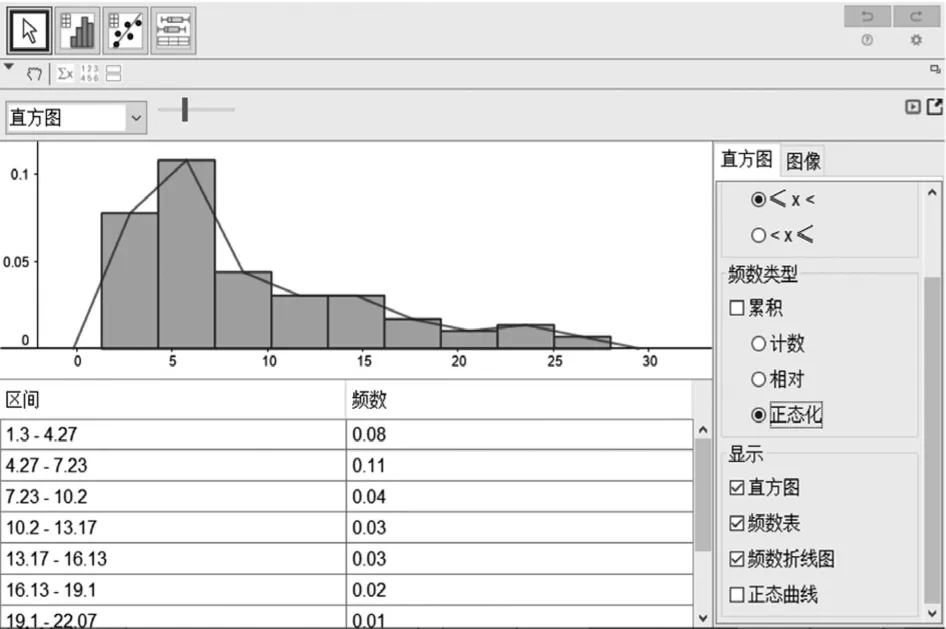
图1
可见,利用GeoGebra能快速获得频率分布直方图及相关的数据,但要想学生获得制作频率分布直方图的获得经验,就需要让学生经历制作频率分布直方图的步骤。由于GeoGebra集代数与几何于一身,所以能利用GeoGebra提供的指令完成相关数据操作。
2 教学片段
片段1:对“频率分布直方图”的整体认识。
学生把教材[5]中“100户居民用户的月均用水量”数据输入表格区中的A列,得到A1至A100共100个数据,利用GeoGebra单变量分析功能,得到直方图。教师引导学生先关注“频数类型”中“频数”“相对”和“正态化”三个选项的区别。
问题1:在三个选项转换的时候,哪些地方变了,那些地方没变?
在三个选项转换的时候,我们可以发现直方图的横坐标是不变的,但是纵坐标发生了变化,从较大的数变成较小的的数。
问题2:在三个不同的选项下拖动滑动条,图形会产生什么变化?这些变化是由哪些因素引起的?
在三个不同的选项下拖动滑动条,我们可以看到小矩形的形状发生了变化。在“频数”选项下拖动滑动条,纵坐标的变化较大,在“相对”条件下拖动滑动条,纵坐标的变化小了,在“正态化”条件下拖动滑动条时纵坐标变化很小,也就是说纵坐标相对比较稳定。
问题3:如果要绘制频率分布直方图,你会采用什么步骤?
设计意图:因为学生在前面的学习中经常利用GeoG-ebra开展探究活动,所以他们能很娴熟地利用GeoGebra自带的统计功能直接绘制出频率分布直方图。以学生已经学习过的频数分布直方图为知识的生长点引入主题,通过三个问题引导学生对该结果进行深入思考,为深入探究频率分布直方图的特征做准备。问题3起到承上启下的作用,同时能培养学生的统计流程意识。
片段二:设置分组。
为了确定每个小矩形的底边,就要对数据进行分组。教材中建议,当数据不超过100个时,常分成5至12组,并且一般取等长的组距,组距力求取整。
问题4:分组时需要哪些前提条件?
通过对片段一中的图形进行观察,学生结合绘制频数分布直方图的经验,知道分组时首先需要知道数据的范围,即要找出数据中的最小值和最大值,利用表格区中的数据创建列表“l1”,利用指令:“最小值(l1)”和“最大值(l1)”得到数据中的最大值记作a,最小值记作b。
问题5:分组时如果事先已经确定组距为k,那么组数应该怎么确定呢?
学生经过讨论后发现,组数可以利用(b-a)/k向上取整获得,在GeoGebra中可以用指令:“ceil((b-a)/k)”获得。
问题6:怎样设置分组区间的端点?
由于组距一般是等长的,而且力求“取整”,所以可以考虑对最小值向下取整,即d=floor(a);对最大值向上取整,即e=ceil(b),从而得到直方图所有区间中的最小值和最大值。用k来表示组距,那么所有分组区间的端点可以使用序列指令得到,即:“序列(d+i*k,i,0,ceil((e-d)/3)”,由此可以得到序列l2,其中的元素就是每个分组的区间端点,同时会创建滑动条k,设置k的取值范围为:从1到ceil((b-a)/3),增量为1。
设计意图:为了能确定分组区间的端点,需要对分组区间的特点进行思考。因为在问题2中,学生发现分组数(或组距)会影响频率分布直方图最后的形状,所有引入了参数k。当我们拖动k时,可以改变k的值。这时GeoGebra就不仅仅是一个展示工具,还是一个思维工具,能把学生的思维结果快速呈现出来,减轻学生的认知负荷。
片段三:列频率分布表。
有了横坐标后,就要计算每个小矩形的高的值。利用GeoGebra的统计指令能够快速进行频数统计以及频率和每个小矩形的高的值的计算。
问题7:怎样利用GeoGebra计算小矩形的高?
因为小矩形的高等于频率/组距,而频率=频数/样本容量,所以可以利用指令:“频数列表(l2,l1)”得到每个分组区间的频数,其结果是序列l3;利用指令:“映射(p/100,p,l3)”将l3中的每个元素除以样本容量100,从而得到每个分组区间的频率,其结果是序列l4。利用指令:“映射(p/k,p,l4)”计算出每个分组区间的频率与组距的比值,也就是每个小矩形的高的值。
问题8:怎样用表格文本指令绘制频率分布表?
首先需要了解频率分布表的组成结构,它一共有三列,第一列是分组区间,第二列是相应区间的频数,第三列是相应区间的频率。
接着就能利用GeoGebra提供的指令构建各列的数据和绘制频率分布表。利用指令:“序列("["+l2(i)+","+l2(i+1)+如果(i<>长度(l3),")","]"),I,1,长度(l3)”获得个分组区间的数学表达式序列l7;分别利用指令:“追加("分组",l7)”“追加("频数",l3)”和“追加("频率",l4)”增加表头,依次得到序列l8、l9和l10;最后利用指令:“表格文本(l8,l9,l10,"v|_")”获得频率分布表,拖动k的滑动条时,频率分布表也会随之而变化,如图2所示。
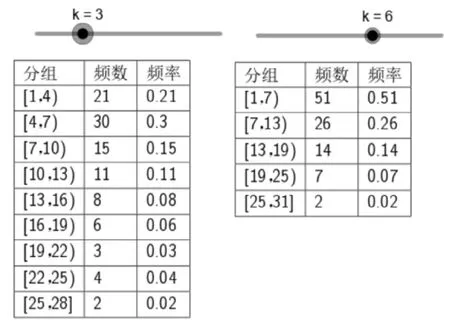
图2
设计意图:由于之前的学习中有利用表格文本列函数值表的活动经验,学生已经能比较熟练的使用指令构造一些序列,所以,在利用GeoGebra构建频率分布表的时候,学生要把注意力集中到各数据之间的逻辑关系上来,这个过程有助于学生对个统计数据关系的理解,同时还能加深他们学统计表格随机性的认识。
片段四:绘制频率分布直方图。
问题9:怎样利绘制频率分布直方图?
频率分布直方图中的每个小矩形的底边是分组区间的端点,纵轴是“频率/组距”,所以可以使用指令:“条形图(最前元素(l2,长度(l3))+k/2,l5)”绘制出频率分布直方图,由于使用条形图指令时,系统会将l2中的元素作为小矩形底边的中点,因此需要将图形平移k/2个单位,也就是加上k/2的原因。点击直方图属性时,还能根据需要设置各小矩形的颜色,如图3所示。图上还能看到“g=1”的标签,这指的是所有小矩形的面积之和为1。
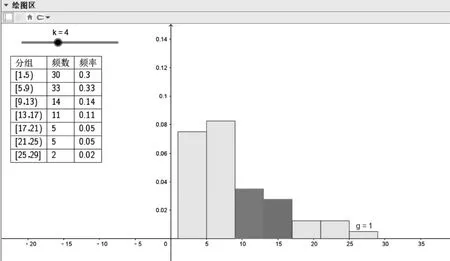
图3
问题10:拖动k的滑动条,观察图形的变化,你发现不同的组数对直方图数据的分布规律有什么影响?
观察可以发现,同一组数据,组数不同时得到的直方图的形状是不尽相同的,当频率分布直方图的组距大、组数少的时候,容易看出数据整体的分布特点,但损失了各组内数据的分布情况;当频率分布直方图的组距小、组数多的时候,保留了较多的原始数据信息,但是图形变得不规则,不容易察觉数据的总体分布特点,如图4(P133)所示。
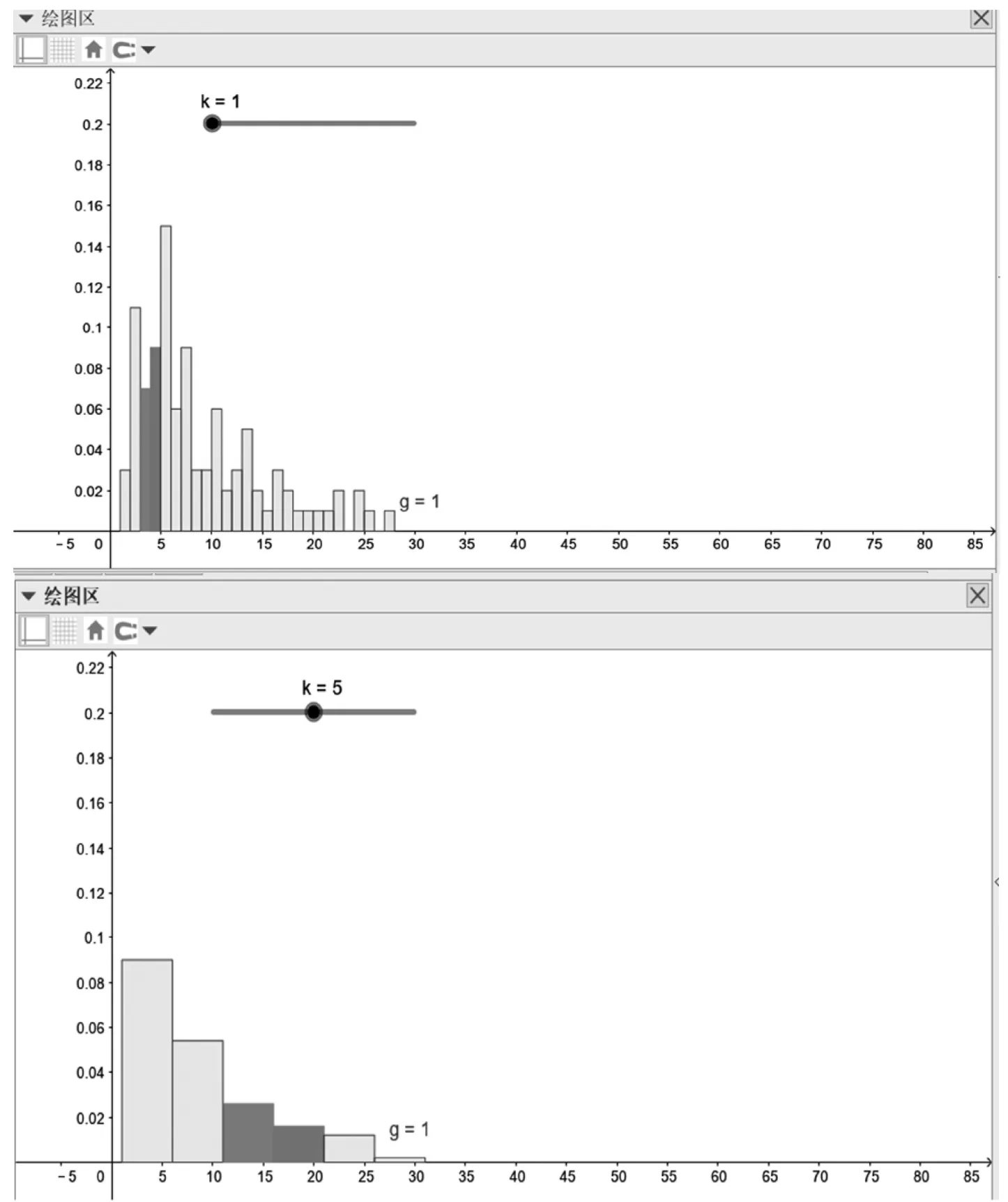
图4
设计意图:在GeoGebra中使用条形图指令制作的频率分布直方图能方便地选择不同的小矩形进行着色,为后续问题讨论提供了方便。通过观察图形地变化,加深学生对统计数据随机性地理解,从而将统计思维与确定性思维进行区分。
片段五:利用频率分布直方图估计均值和方差。
问题11:怎样利用频率分布直方图估计均值和方差?
使用频率分布直方图估算均值和方差时,将同一分组区间里的数据统一为该区间的中点的值,所以可以使用指令:“ave=总和((l2(i)+k/2)l4(i),i,1,长度(l3))”来获得平均值,使用指令:“sqrt(总和((l2(i)+k/2-ave)2*l4(i),i,1,长度(l3)))”获得标准差。
问题12:拖动滑动条k,观察比较利用直方图获得的均值和标准差与利用单变量分析得到样本的均值和标准差之间的区别?为什么会造成这种区别?
通过GeoGebra自带的单变量分析得到的样本均值是8.79,标准差是6.2047,如图5所示,当拖动滑动条时可以发现,由频率分布直方图估算得到的均值和标准差都和自带的数据有差异,这是因为频率分布直方图已经将数据信息做了简约化处理,是以损失一部分信息为代价的,尽管这样,估算的结果与真实值相差其实并不大。

图5
设计意图:通过估算平均值和方差,并通过变化k值来比较这两个值与“真值”的差异,让学生能亲切地感受到统计思维与确定性思维的区别,加深统计结果随机性的理解。
3 结语
统计内容的学习有一个螺旋上升的过程,义务教育阶段的统计内容以描述性统计为主,着重在感性层面认知统计思维,学习方式偏重于计算;而高中阶段的统计内容将过渡到推断性统计,着重于通过理性层面认知统计思维,学习方式偏重于统计推断。频率分布直方图一课具有很强的实践性,虽然内容难度不大但统计思想深刻。学生利用GeoGebra进行操作实践和动态图形的分析,能更好地理解频率分布直方图的特点,能更深刻的理解统计思维与确定性思维的区别,加深统计结果随机性的理解。
