绳牵连问题中加速度关系的求解

段石峰

(湖南省长沙市周南中学，湖南 长沙 410201)

1 绳牵连问题中的加速度关系

例：如图1所示，圆环套在固定竖直杆上，用轻绳连接后跨过轻质定滑轮与物块相连，开始时圆环与滑轮等高。杆与滑轮间的距离为l，绳和杆足够长，不计一切阻力。现将圆环由静止释放，求圆环加速度a1和物块加速度a2之间满足的关系式。

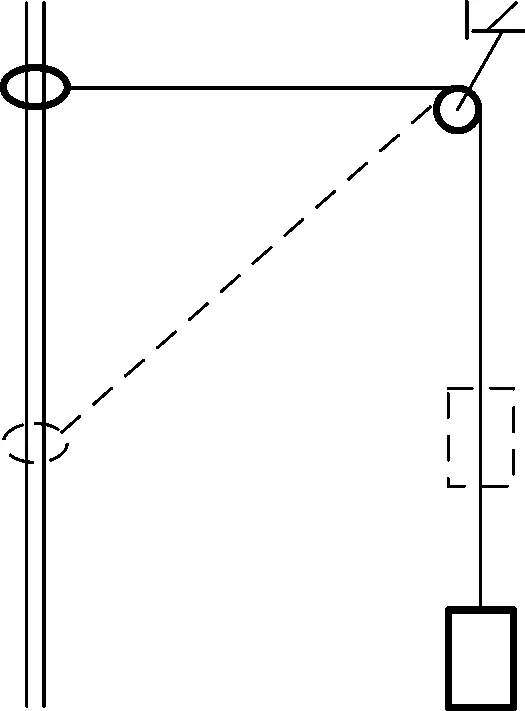
图1

分析：如图2所示，设圆环下降到某一位置时绳与水平方向的夹角为θ，圆环和物块的速度分别为v1和v2，将圆环的速度v1分别沿绳方向和垂直绳方向进行正交分解，由于绳不可伸长，圆环和物块沿绳方向的速度大小相等，有：v2=v1sinθ。

图2

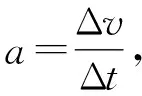
1.1 矢量图解法

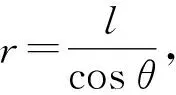
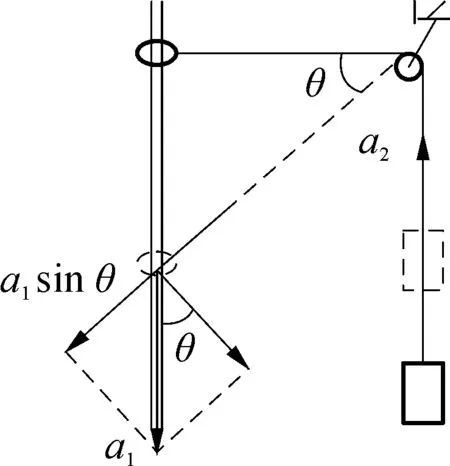
图3

1.2 数学求导法

1.2.1 对速度关系式求导

1.2.2 对几何关系式求导

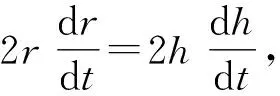
2 求解绳牵连问题中的的最大速度

在上述问题中，若已知圆环的质量m1=3 kg，物块的质量m2=5 kg，杆与滑轮间的距离l=2 m，重力加速度取g=10 m/s2，求圆环和物块的最大速度。

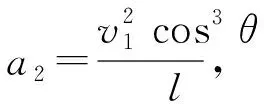
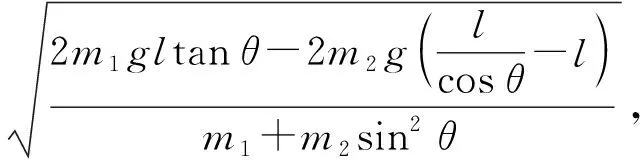
对其求导并令导数为0，也可进行求解，但难度也较大。笔者利用《几何画板》软件绘制出函数图像，以求出数值解，如图4所示，实线为v1-θ图像，虚线为v2-θ图像。由图4可知：当θ≈0.471 rad≈26.99°时，圆环的最大速度约为3.017 m/s；当θ≈0.781 rad≈44.75°时，物块的最大速度约为1.838 m/s。

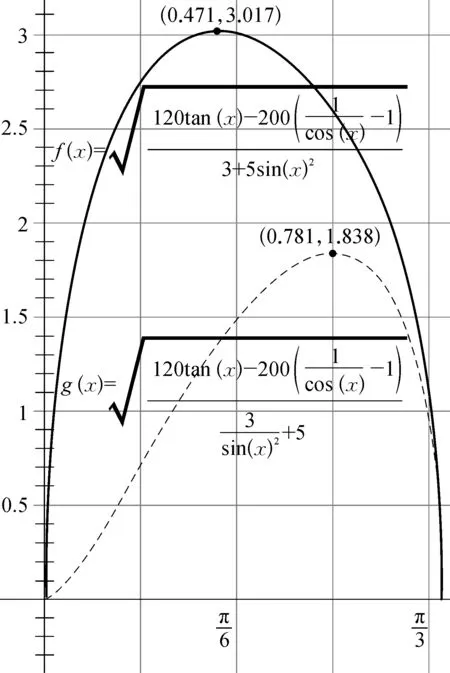
图4

3 结语

绳牵连和杆牵连问题中的加速度关系具有类似的特点，不仅要考虑加速度矢量的分解，还要考虑由于转动而引起的向心加速度。当然，高中物理不要求定量求解加速度大小不同的连接体问题，一般地不要求学生掌握，因此在常规教学中应该尽量回避。但没有超出高中学生的能力范围，对于学有余力的学生，可以先采用矢量图解法进行定性分析，再采用数学求导法进行定量计算。