内部构造具有安全保障体系的系统解分析

尹 慧, 冯 雪, 唐锎远

(1.沈阳城市建设学院 基础教研部, 辽宁 沈阳 110167; 2.空军航空大学 航空基础学院, 吉林 长春 130022)

0 引言

系统解的分析涵盖稳定性与可靠性等方面,与国民经济建设、国防建设的关系极为密切,大到卫星、飞机、导弹,小到家用电器均与可靠性息息相关.最早被研究的领域之一是机器维修问题,另一个重要的研究领域是将更新理论应用于系统更换问题.近些年来,有大量文章对具有人为操作错误的人机系统的可靠性和可靠度作了细致的研究,可靠性设计和分析已成为许多部门产品发展工作中不可缺少的重要一环.并且可靠性是决定一个系统(或子系统)是否能够在整个系统中被运用的重要指标之一.

Dhillon用拉普拉斯变换的方法研究了内部构造安全保障体系系统的模型[1],冯雪等用半离散逼近方法将一个抛物型偏微分方程化为一个矩阵常微分方程,并保持了原问题重要的物理意义[2-3].离散后的数学模型适合于计算机的计算和模拟.本文在系统解的唯一性[4]研究内容的基础上运用线性代数、泛函分析等理论方法研究了系统稳定性和可靠性,对研究该系统的解做了更为深入的分析.

1 系统模型介绍

本文讨论的冗余机器系统是由两台相同机器和一个安全保障体系组成,且其可修机器和安全保障体系在应用时是完好无损的.当机器都故障时整个系统故障.各状态间的转换关系如图1所示.

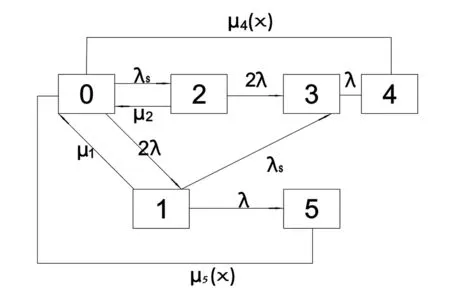
图1 系统状态转移

图1中的数字和字母表示相关的系统状态.i=0表示两台机器和安全保障体系均正常运行;i=1表示台机器和安全保障体系正常运行,另一台机器故障;i=2表示两台机器正常运行,安全保障体系故障;i=3表示 一台机器正常运行,安全保障体系故障,另一台机器故障;i=4表示 两台机器与安全保障体系均故障;i=5表示两台机器故障,安全保障体系正常运行.

系统模型可由以下积分-微分方程描述:

(1)

(2)

(3)

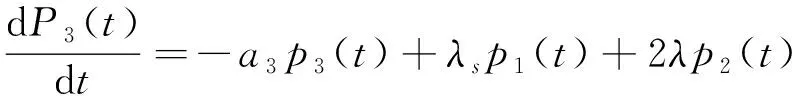
(4)

(5)

其中

a0=2λ+λs,a1=λ+λs+μ1,a2=2λ+μ2,a3=λ.

相关的边值条件如下

p4(0,t)=λp3(t)

(6)

p5(0,t)=λp1(t)

(7)

相关的初始值如下

p0(0)=1,p1(0)=p2(0)=p3(0)=p4(x,0)=p5(x,0)=0

(8)

其中λ表示机器定常故障率;μi表示状态i定常修复率;λs表示与机器相关联的安全保障体系的定常故障率;pi(t)-t为时刻系统处于状态i时的概率(i=0,1,2,3);pi(x,t)-t为时刻系统处于状态i且已修复时间x的概率,并且pi(x,t)仅在t>0时有意义(i=4,5);μi(x)为系统处于状态i,修复时间x时的系统修复率(i=4,5).且满足

2 系统解的稳定性

2.1 泛函分析处理

下面在Banach空间中用的抽象的Cauchy问题的形式来描述该系统.

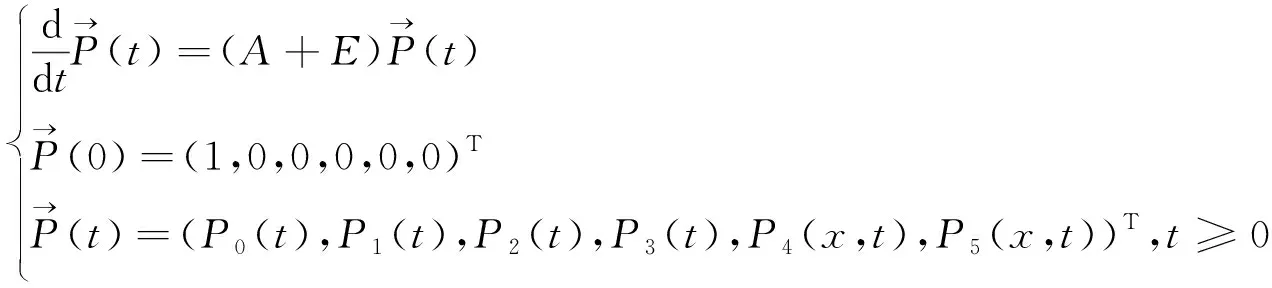
(9)

2.2 系统非负时间依赖解存在且唯一

柳京爱等运用初等方法得到系统非负强解的存在且唯一性[5-6].本文采用算子半群方法,对前面所建立的数字模型确立一正压缩c0半群,得到系统存在唯一非负动态解.

下面，分析具有内部构造安全保障体系系统解的稳定解.

假设1该系统存在唯一非负时间依赖解P(x,t).

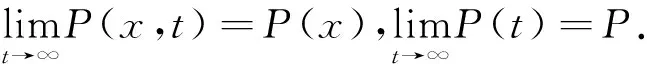
定理1 设A、E定义如前,那么

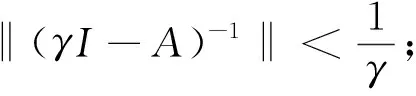
2)D(A)在X中稠密；

3)A+E生成一正压缩c0-半群；

4) 正半缩c0-半群就是算子T(t).

由耗散算子的定义知为耗散算子,结合条件3)、Philips定理及系统定性分析[7],知算子生成一正压缩c0-半群,再由生成c0-半群的唯一性,即知此正压缩c0-半群就是T(t).

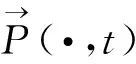
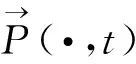
由定理1与定理2得到

则有

2.3 可修复系统解的渐进稳定性

在这部分讨论系统解的渐进稳定性,前面讨论了系统存在非负稳定解,以及系统时间依赖解.当t→∞时,收敛于此稳定解,因此证明了可修复系统的渐进稳定性.

定理3 0是算子A+E的简单特征值.

定理4 {r∈C|Rec>0或r=ia,a∈R,a≠0}属于算子A+E的预解式.

3 系统算子特征值的存在性

3.1 系统算子非零特征值的存在性

得到有关于p0,p1,p2,p3方程组行列式如下,

易证|D|有界,且当γ>0时,|D|≠0.

3.2 系统非零特征值的存在性

由冯雪等对系统特征值的分析可知[8],预解式有极点等价于|D|=0.

其中

b0=γ3+(a1+a2+a3+λs)γ2+(4λλs+a1a2+a1λs+a2a3+a3λs+a1a3)γ+

2λλsa1+2λλsa2+a1a2a3+a1a3λs,

b4=4λ2λsγ+2λ2λsa1+2λ2λsa2,

b5=2λ2γ2+2λ2(a2+a3)γ+2λ2a2a3,

γ3+(a1+a2+a3+λs)γ2+(4λλs+a1a2+a1λs+a2a3+a3λs+a1a3)γ+2λλsa1+

2λλsa2+a1a2a3+a1a3λs<0

(10)

4λ2λsγ+2λ2λsa1+2λ2λsa2<0

(11)

2λ2γ2+2λ2(a2+a3)γ+2λ2a2a3<0

(12)

为了计算简便,举例证明.

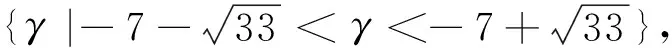
3.3 特征值与特征向量一一对应

4 系统的可靠性

4.1 方程的转换

令μi(x)=μ3(i=4,5),

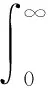
(13)

(14)

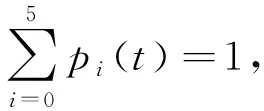
原方程组可描述为Banach空间X中抽象Cauchy问题，

(15)

4.2 单调性证明

下面证明p0(t)是严格单调函数.

定理5 当λs=λ,μ1=μ2=μ3=μ时,p0(t)为严格单调减函数.

证明在上述条件下,方程(12)可化为

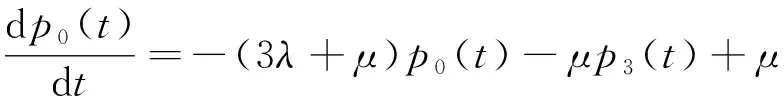
(16)

p0(t)为单调递减函数,即

（一）广开言路，听取民意。在“为灾区献爱心”的志愿活动中，学校大队部充分尊重队员的“主人翁”地位，积极发挥队员的主观能动性，让队员直接参与活动的决策，广泛听取队员的心声。首先由学校大队部召开各中队干部会议，在会上提前传达志愿活动的主题，接着由各中队自主思考、自主讨论、收集和整理意见，然后学校大队部再整合大家意见，确定活动实施方案。这样一来，志愿活动的策划方案自始自终都体现了少先队员的主体地位，并且融汇了每个少先队员的想法，提升了少先队员参与活动的积极性。在这次“为灾区献爱心”的志愿活动中，学校根据各中队的意见，决定开展“中队大义卖”的活动。

(17)

解得

(18)

4.3 系统可靠性分析

下面分两步对系统的可靠性进行分析.

1) 当0

而λs=λ,μ1=μ2=μ3=μ4=μ5=μ(i=4,5),由微分方程的求解[9-10]可得原方程的解为

则

当t=t0时,

显然p(t0)≥p0(t0),t0∈(0,t),其中

c11=eλ1t+a(-3λ-μ-λ1)+ba41+cb41,

c21=a2λ+ba21+cb21,c31=aλ+ba31+cb21,c41=ba41+cb41.

而

a11=(3λ+μ+λ2)(3λ+μ+λ1),a21=2λ(-5λ-2μ-λ1-λ2),

a31=λ(-5λ-2μ-λ1-λ2),a41=4λ2,

b11=(-3λ-μ-λ3)a11-μ41,b21=2λa11-(2λ+μ+λ3)a21,

b31=λ11-(2λ+μ+λ3)a31,b41=λa21+2λ31-(λ+λ3)a41,

h11=-λ(2λ+μ)2|A|-1,h12=μλ(2λ+μ)|A|-1,

h13=2μλ(2λ+μ)|A|-1,h14=μ(2λ+μ)|A|-1,

|A|=(2λ+μ)(6λ3+9λ2μ+μ2λ),

λi(i=1,2,3,4)为A的特征根,Qi是各已知量代数表示.

2) 当x≥x0,t0≤t≤∞时,此时令μ4,μ5(常数)μ4<μ5,此时原方程中解的初值为(p0(t0),0,0,0)T.

5 结语

本文对具有内部构造安全保障体系系统模型的方程,使用泛函分析中的压缩映照原理及不动点定理证明该系统解的唯一性、对系统非负时间依赖解的存在且唯一性.并对该系统解的非零特征值的存在以及特征值与特征向量一一对应关系进行的证明.在此基础上对系统的可靠性分析进行了证明,即得到系统的瞬态可靠性不小于牢固可靠性的结论.