带启动时间及不耐烦策略的多重休假M[X](λ1,λ2)/G/1排队

王 莉, 朱翼隽

(1.宿迁学院 文理学院, 江苏 宿迁 223800; 2.江苏大学 数学科学学院, 江苏 镇江 212013)

0 引言

随着排队论理论的逐步发展和完善,学者们根据在实际应用中出现的各类情况,分别对各种排队模型进行研究,对休假排队系统的研究[1-3]也逐渐增多,其中具有代表性的M/G/1型休假排队系统是典型的一类,学者们在此基础上纷纷构造了不同的模型[4-9]并给出了一系列有价值的观点和研究理论.比如在M/G/1型休假排队模型中考虑闲期、启动期、不耐烦策略、负顾客、单重休假、多重休假等各种因素,如朱翼隽,徐剑研究的多重休假的M/M/c排队系统[2].这些模型是在经典M/G/1排队的各种边界状态变体基础上加入了一些条件进行研究的.

本文在前人研究的休假模型基础上,建立了一个到达率不同并且是批量到达的M/G/1多重休假排队模型,并在模型中考虑了服务台工作前有启动期的情况.

1 模型描述

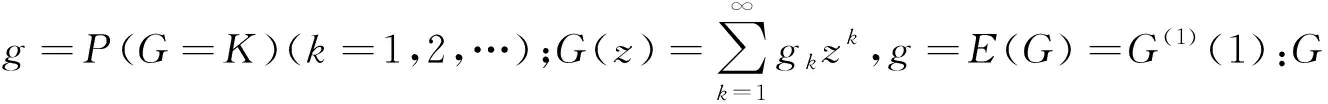
一个V内进入系统的顾客数为零的概率是

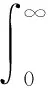
设Ln为接受完服务的第n个顾客离开后系统中的顾客数,n=0,1,…,则{Ln,n≥1}是队长过程的嵌入Markov链,从而有如下关系

(1)

其中An+1为服务第n+1个顾客时进入系统的顾客数,且A1,A2,…,An,…独立同分布;批量到达的顾客数服从复合泊松分布.一个服务期内到达的批量数Ag和顾客数A满足如下关系

A=G(1)+…+G(Ag)，

其中{G(n),n=1,2,…,Ag}与G独立同分布;得A的母函数为

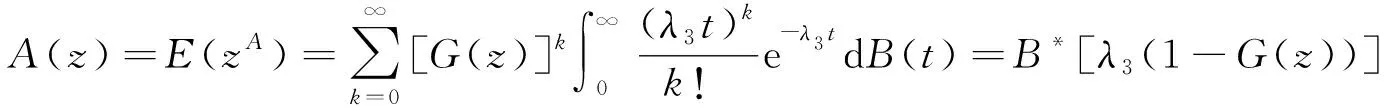
(2)

先求如下分布

其中Qb为转入忙期时系统中过的顾客数,且

ξi=P{进入i个顾客|一次假期内有顾客进入系统}=

从而可以求出Qb的母函数

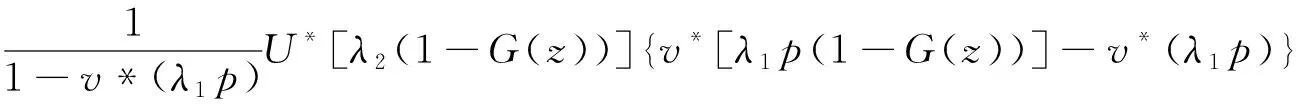
(3)

由上式可知

2 稳态队长和等待时间的随机分解

当ρ=λ3gμ-1<1时,系统达到稳态.记

定理1 设ρ<1时,分解式L=L0+Ld成立,其中L0,Ld相互独立,则L0的母函数[3]

附加队长Ld的母函数为

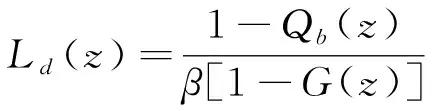
(4)

证明在第n个顾客离去时有无顾客的条件下,根据式(1),两边取母函数,得

E(zLn+1)=E(zLn+An+1-1|Ln>0)P(Ln>0)+E(zQb+An+1-1|Ln=0)P(Ln=0)=

因为{Ln,n≥0}独立同分布,将式(2)和式(3)代入上式,整理得

{1-[1-v*(λ1p)]-1U*[λ2(1-G(z))][v*(λ1p(1-G(z)))-v*(λ1p)]}

(5)

使用正规化条件L(1)=1及L’Hospital法则得到π0=(1-ρ)β-1.将其代入式(5),得到

(6)

由上式可得到式(4).

由定理1，容易给出下列均值公式，

定理2 若ρ<1,则稳态等待时间W可分解成两个独立随机变量之和W=W0+Wd,其中W0的LST[3]

附加延迟Wd的LST

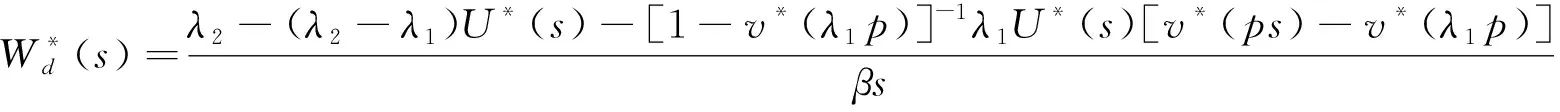
(7)

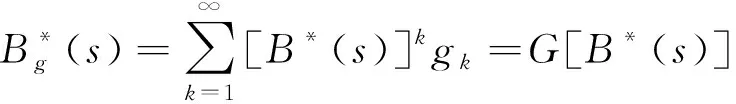
(8)

根据式(6),服务完一个大顾客后系统中大顾客数的概率母函数为

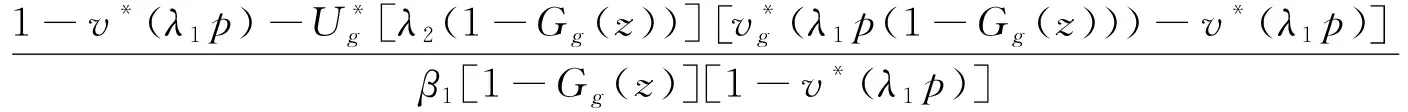
(9)

其中β1=β,Gg(z)=z.

当λ1≠λ2≠λ3时,利用同样方法化简，可得

(10)

如果在大顾客中排在一个目标顾客之前的逗留顾客数为G-,利用更新过程[10],两个连续更新点间隔为批量长G,而G-概率分布和母函数分别为

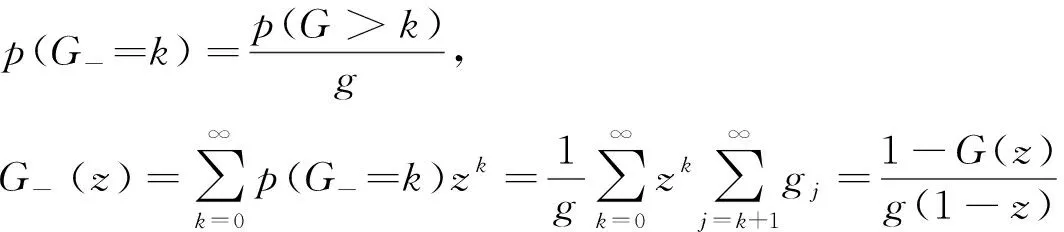
(11)

从而可以得到批量等待时间Ws的LST

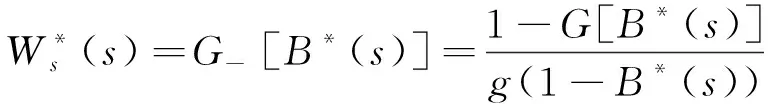
(12)

再根据式(10)和式(12)，有

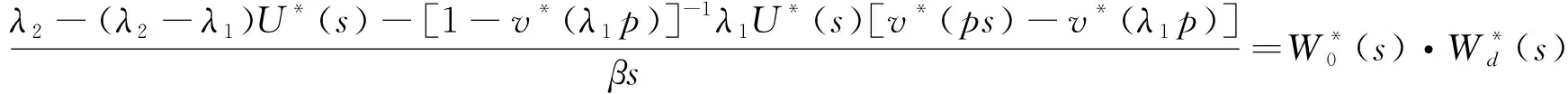
(13)

从而得出式(7),证毕.

由式(7)和式(13)，容易给出下列均值公式

从定理1和定理2不难看出当λ1=λ2=λ时,E(Ld)=λE(Wd)满足Little公式.

3 忙期和忙循环

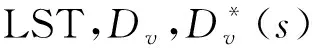
从而得出平均忙期

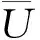
特殊地,当λ1=λ2=λ3=λ时,一个忙循环的平均长度是

记PB,PV,PU为稳态下服务、休假及启动在任一时间点的概率,由更新报酬定理可得

4 在线期分析

在线期是指一个休假结束直到下次休假开始的这段时间.忙期和启动期均属在线期.记Ts代表在线期的长度,易得在线期的均值为

5 应用案例

例1 带启动时间及不耐烦等待的多重休假M/G/1排队.

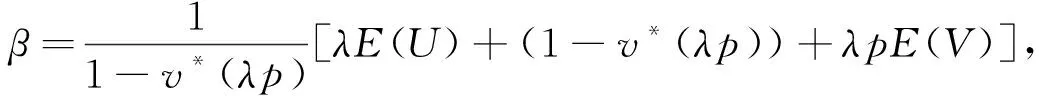
例2 带启动时间的多重休假M/G/1排队.

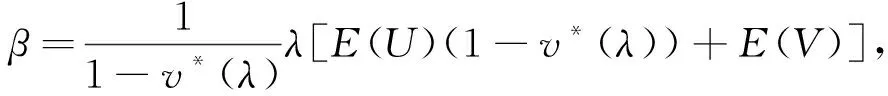
与马占友[8-9]的研究结果完全吻合.

例3 带启动时间及不耐烦等待得多重休假MX/G/1排队.

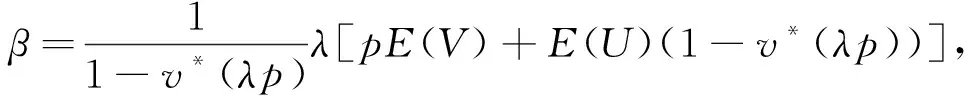
与于艳辉等[6]的研究结果吻合.

以上特例具体指标的结果，可以再次验证本模型的可行性和正确性.

6 结论

模型中考虑到多重工作休假系统在实际应用中的复杂多变的情形,将简单的休假模型复杂化,添加了批量到达、启动和不耐烦策略这些实际中的控制因素,建立了一个多重工作休假排队系统的新模型,通过运用基本的排队理论和方法得出了新模型的一系列重要的性能指标,通过几个特殊模型的验证也得出了该模型更具一般性,为实际运用提供了理论依据,同时为工作休假进一步深入的研究也提供了参考.