一类Laplace方程预定夹角问题的边界梯度估计

马春梅, 司雨欣, 吴婷婷

(新疆师范大学 数学科学学院, 新疆 乌鲁木齐 830017)

0 引言

在二阶椭圆型偏微分方程的研究过程中, 边值问题的解的存在性是最重要的问题之一.边值问题主要分为Dirichlet问题,Neumann问题与斜导数问题,而解决边值问题解的存在性问题的关键在于先验估计,即解的梯度估计,最大模估计等.梯度估计中的Dirichlet问题已有广泛的研究,1969年Serrin[1]给出了二阶拟线性椭圆型偏微分方程的Dirichlet问题的解的存在性的证明.2001年Gibarg,Trudinger等人[2],研究了具有Dirichlet问题的可解性和线性方程解的一般性质.对于预定夹角问题,也有相关研究,Simon-Spruck[3],Gerhardt[4],Lieberman[5]等人利用分部积分法用给出了高维预定夹角问题的梯度估计.

2014年,徐金菊[6]综合利用Spruck[7],Wang[8],Lieberman[5]所发展的Bernstein技巧给出了Laplace方程Neumann问题的梯度估计,即

Δu=f(x,u),x∈Ω,

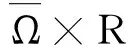
2019年,刘海燕研究如下Laplace方程在Neumann边值问题的梯度估计[9],即

Δu=f(x,u,Du),x∈Ω,

受徐金菊[6]的启发,本文考虑如下形式的一类Laplace方程预定夹角问题的梯度估计

Δu=f(x,u,Du),x∈Ω,

鉴于椭圆型偏微分方程解的梯度估计证明[10-11],本文利用徐金菊所使用的Bernst-ein技巧,推导出Laplace方程中关于f依赖于x,u,Du时预定夹角的解的全局梯度估计的结果.

1 预备知识

为了证明简便,本节将介绍一些基本概念及性质.设Ω是Rn中的有界区域n≥2,∂Ω∈C3,γ是∂Ω的单位内法向.令

d(x)=dist(x,∂Ω),

Ωμ={x∈Ω:d(x)<μ}.

|Dγ|+|D2γ|≤C(n,Ω),

引入记号cij=δij-γiγj.对任一Rn中向量ζ,记ζ′为ζ的切向部分,其第i个分量定义为

梯度Du的切向量记为D′u,则

引理1[6]研究如下二次型

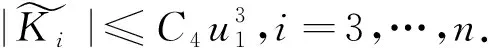
|Du|(x0)=u1(x0)≥C10,

则以下结论正定，

ζT=(1,…,1),ηT=(e3,…,en).

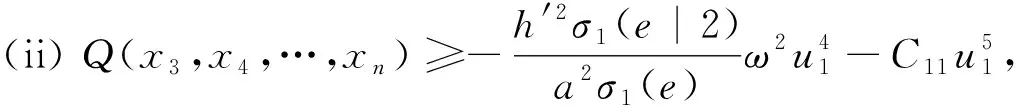
2 主要结果

考虑如下Laplace方程的预定夹角问题

Δu=f(x,u,Du)x∈Ω

(1)

(2)

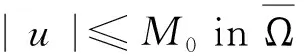
(3)

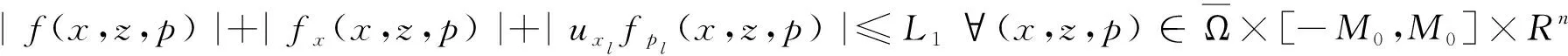
(4)

引理2[12]设u∈C3(Ω)为式(1)的解,则对任一区域Ω′⊂⊂Ω有

其中M1只依赖于n,M0,dist(Ω′,∂Ω),L1.

则存在小的正常数μ0使得

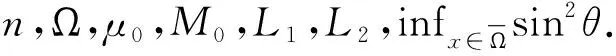
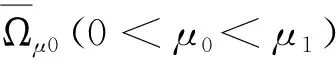
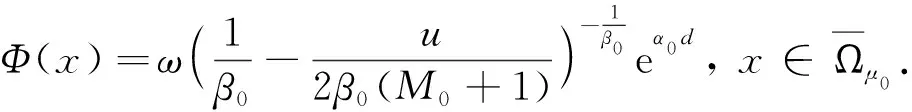
并且C0是只依赖于n,Ω的正常数.令

φ(x)=logΦ(x)=logω+h(u)+g(d).

其中

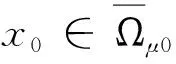
情形1x0∈∂Ω,由Hopf 引理得|Du|(x0)有界,对φ求法向导数,再利用边界点性质即可得到,证明过程可参照文[6].

情形2 若x0∈∂Ωμ0∩Ω则归结为内部梯度估计.由引理2,可得

情形3 若x0∈Ωμ0,证明|Du|(x0)有界.

由以上选取,分3步完成定理证明.以下计算都将在x0点进行.

第1步: 先推导△φ

对φ微分两次,得到

由φi(x0)=0,有

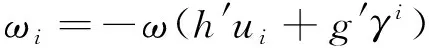
(5)

由式(5),可得

根据坐标系的选取和方程(1),有

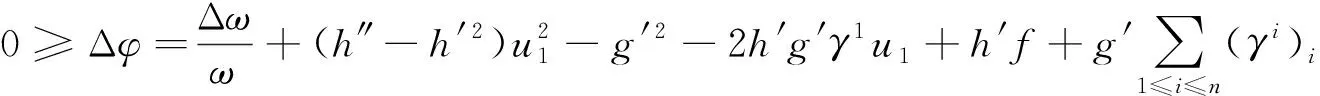
(6)

由ω的定义,对ω微分两次,并根据坐标系的选取,有

(7)

由v的定义,在x0点,可得

vvi=u1u1i

(8)

由式(8),得

(9)

将式(9)代入式(7)可得

(10)

因为Dkf=fxk+fuuk+fplulk,由方程(1)和式(10)及坐标系的选取,将式(10)代入式(6),可得

0≥Δφ=:I1+I2+I3

(11)

由于

因为

因此，式(11)中uij的二次项为

uij的一次项为

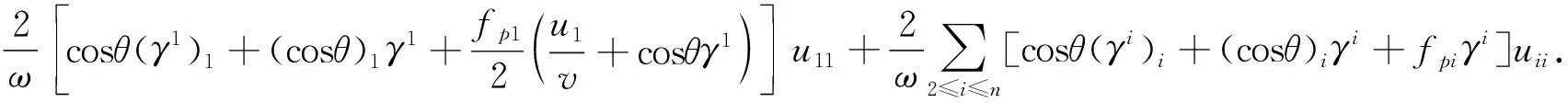
其他剩余项为

由|cosθγ1|≤|cosθ|≤b0<1,在x0点,可得

从而,得到

I3≥(h″-h′2)u12-C1u1.

第2步: 利用条件φi(x0)=0处理I1,I2并得到式(18),由式(5)和式(8),及坐标系的选取,得到

(12)

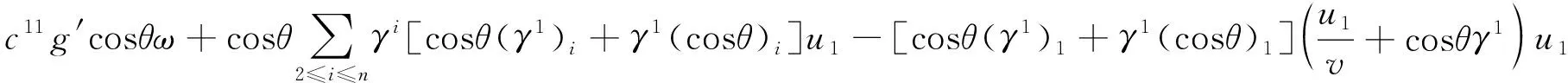
(13)

(14)

将式(14)代入式(12)和式(13),得到

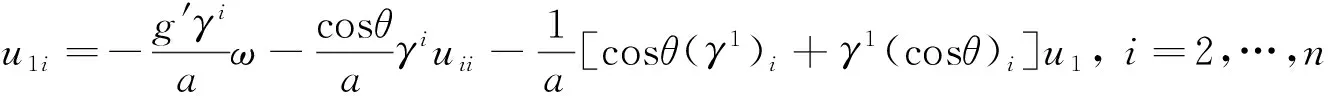
(15)

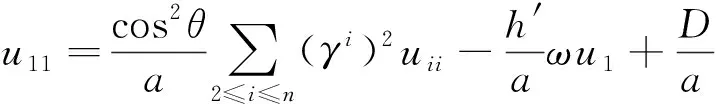
(16)

其中

得到估计|D|≤C2u1.

由方程(1)和式 (16)，可得

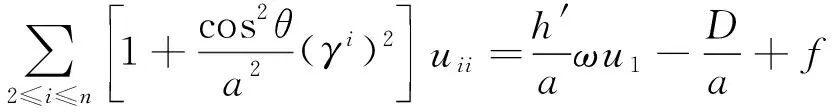
(17)

公式化简I1,I2,代入式(11)得

0≥Δφ=:Q1+Q2+Q3

(18)

其中uij的二次项为

令

(19)

uij的一次项为

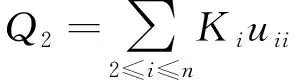
(20)

Q3=(h″-h'2)u12+Ο(u1).

第3步: 主要计算Q1,Q2,并通过引理1完成定理证明.由式(17)有

(21)

将式(21)代入Q1,得到

(22)

其中

化简Q2，将式(21)代入式(20),得

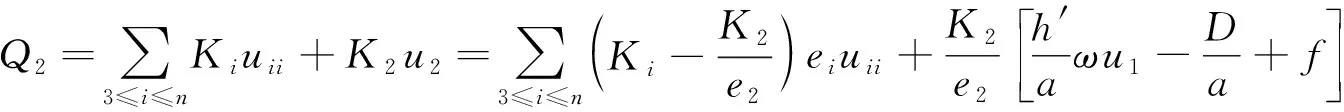
(23)

由式(21)和式(22),得

其中

以及

(24)

|R|≤C5u1.

根据引理1,如果存在正常数C6使得

|Du|(x0)≥C6

(25)

则有

(26)

结合式(25),将式(26)代入式(18)，得到

从而存在正常数C9使得

|Du|(x0)≤C9

(27)

由情形1,情形2和式(27),得到

|Du|(x0)≤C9,x0∈Ωμ0∩∂Ω.

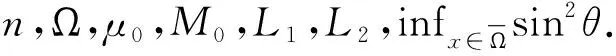
|Du|(x)≤M2,x∈Ωμ0∪∂Ω.

最后得到

定理得证.