利用加速度信号重构位置反馈的振动控制方法
2022-12-16李金辉朱会杰赵洪涛孟兆海
李金辉,朱会杰,赵洪涛,孟兆海
(1.陆军研究院五所,无锡 214035;2.天津航海仪器研究所,天津 300131)
随着北京S1 示范线、长沙机场线、凤凰旅游专线等的建设和运营,磁浮列车的低噪、安全等优势使其具备良好的应用前景。然而磁浮系统还存在磁浮列车-支撑梁耦合自激振动难题。对于高铁等轮式列车,当其零速停靠在支撑梁上时,支撑梁会出现挠性变形,但不会出现持续的、自发的振动。
当磁浮列车低速通过或静止在支撑梁时,除挠性变形外,还可能出现持续的、自发的垂向振动。德国TR 系统、日本HSST 系统、中国S1 原型系统、韩国UTM 系统和美国AMT 系统,均出现过此类自激振动现象[1]。自激振动降低了支撑梁的使用寿命和安全性,极端情况下导致电磁铁与支撑梁的碰撞,影响磁浮列车的安全运行。
为了解决磁浮列车-支撑梁耦合系统自激振动难题,学者们提出了多种解决方案。从避免自激振动的方案来看,可总结为强化支撑梁和优化悬制算法两大类方法。
强化支撑梁方面,主要包括增加支撑梁的模态阻尼系数、增大支撑梁的线密度、降低支撑梁的一阶模态频率等[2]。然而强化支撑梁的方法显著增加了磁浮系统的造价,降低了综合竞争力,不利于商业推广。优化控制律方面,王志强等提出了跟踪微分器[3]等算法,可以降低自激振动的幅值。李金辉等提出在状态反馈控制方法中增加一个吸振模拟分量[4-5],这种方法可在动态检测振动频率的基础上延后压制自激振动幅度。段宇星[6]等在无人机平台振动方面提出了隔振优化设计,也值得借鉴。
本文在借鉴磁浮列车-支撑梁耦合系统最小动力学模型的基础上,分析了采用磁通强度作为内环的系统框图和基于根轨迹的系统稳定性,提出剔除桥梁位移反馈并用加速度信号重构电磁铁位置信号的控制方案,并开展数值仿真分析和实验研究以验证控制方案的有效性。
1 悬浮系统建模
建立如图1 所示的磁浮列车-支撑梁耦合系统最小动力学模型[7]。
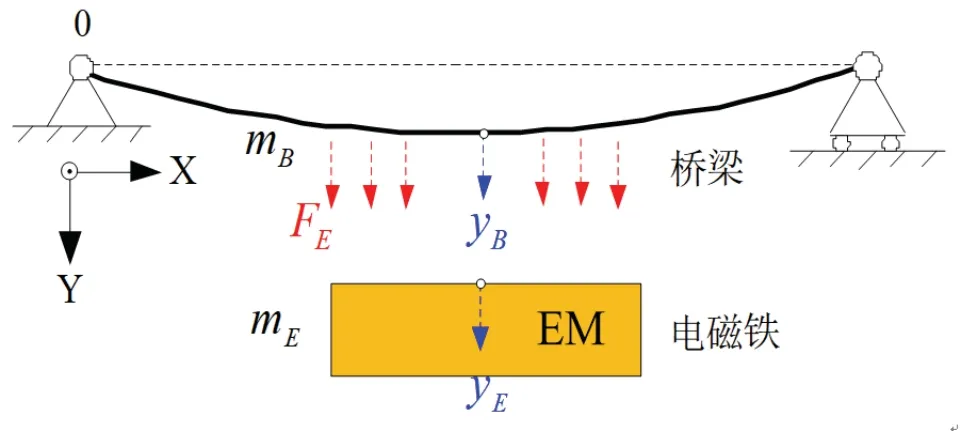
图1 简化的磁浮列车-支撑梁耦合系统示意图Fig.1 Simplified maglev train-bridge coupled system
其中,mB、mE分别为支撑梁和电磁铁的等效质量,yB、yE分别为支撑梁和电磁铁的垂向位移,FE为电磁铁吸引支撑梁的电磁力。当采用悬浮电流i(t)作为主控状态变量时,其电磁力FE(t)和电压u(t)方程为式(1)所示。其中,μ0为真空磁导率、A为电磁铁的极面积、N为悬浮线圈的匝数、R为悬浮线圈的电阻。

当采用磁量通B(t)作为主控状态变量时,其电磁力FE(t)和电压u(t)方程为:
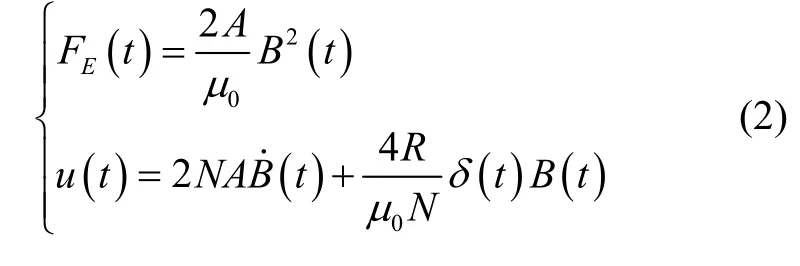
根据式(1)可知,当采用电磁铁中的电流作为内环控制量时,电磁浮力FE(t)与悬浮电流i(t)的二次方成正比,与悬浮间隙δ(t)的二次方成反比,因此电磁浮力FE(t)由悬浮间隙δ(t)和电流i(t)综合决定。
根据式(2)可知,当采用悬浮气隙间的磁通强度作为内环控制量时,电磁浮力FE(t)与磁通强度B(t)的平方成正比,是磁通强度B(t)的单变函数,更有利提出改善磁浮列车-支撑梁耦合系统稳定性的控制解决方案。
在控制领域,状态反馈控制器应用最为广泛[8,9],采用基于磁通内环的状态反馈控制算法,即:

其中,B(t)为悬浮间隙中实际的磁场强度,BE(t)为悬浮间隙中期望的磁场强度,kp、kd、ka、kB分别为反馈增益,uDC为稳态悬浮电压值,B0为稳态磁场强度。当采用如上状态反馈控制器时,系统框图如图2。其中,kF=4AB0/μ0,黄底方框表示电磁铁电压方程。
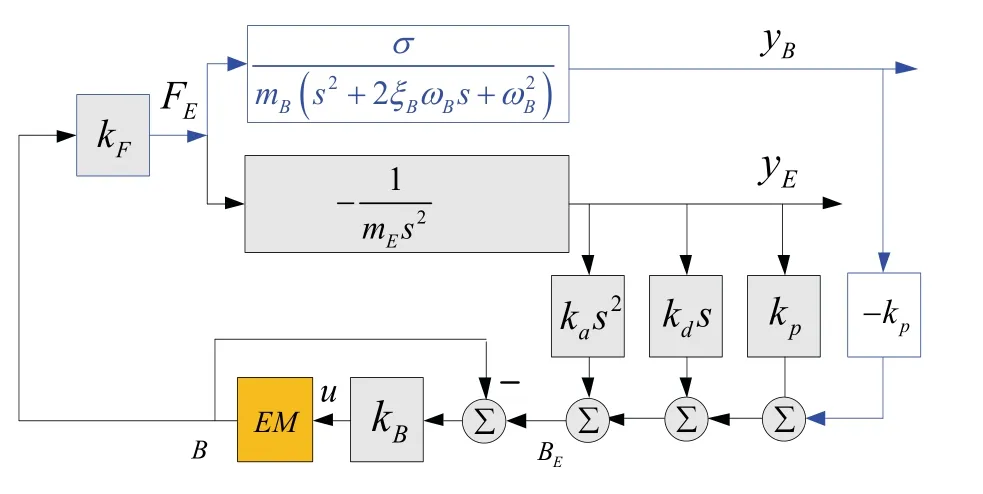
图2 采用磁场强度内环状态反馈时的系统框图Fig.2 System diagram when the magnetic intensity as an inner state is adopted
根据图2 可知,悬浮间隙中期望的磁场强度BE(t)为电磁铁的垂向状态,y E(t)与支撑梁的位移y B(t)的线性组合。下面对磁浮列车-支撑梁耦合系统的稳定性进行分析。
2 稳定性分析
如式(4)所示,将期望磁通BE(t)分解为BE1(t)和BE2(t),其中BE1(t)为悬浮电磁铁的垂向加速度、垂向速度和垂向位移的组合,BE2(t)为支撑梁的垂向振动位置反馈。
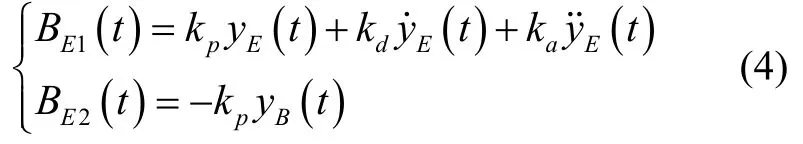
依据悬浮控制律式(3)所示,基于可加性原则,系统框图可以化成如图3 所示的框图。可定义电磁浮子系统的前向通道GE(s)和反馈通道H E(s)为:
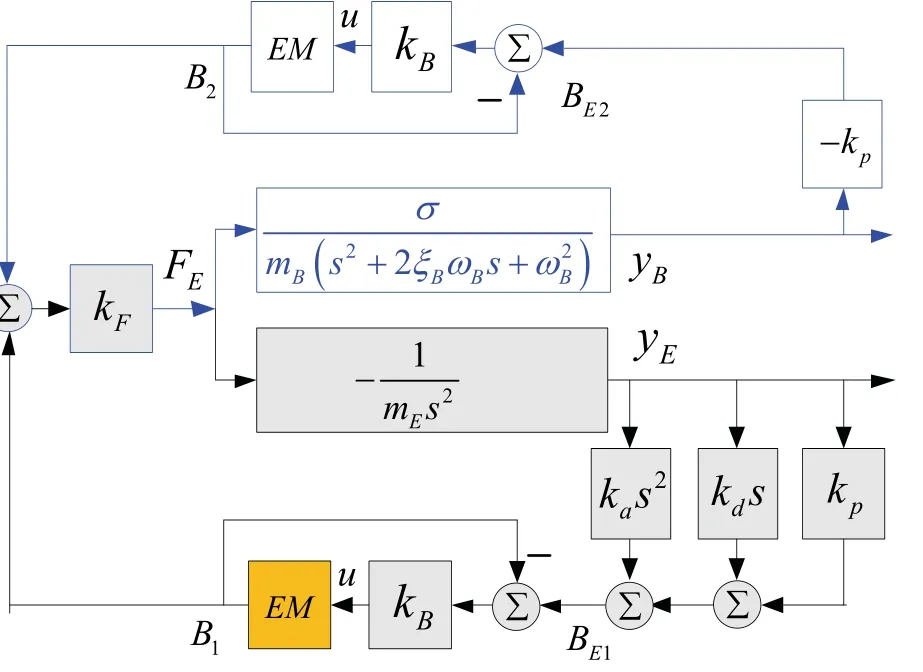
图3 变换后的系统框图Fig.3 Transformed system diagram

定义支撑梁子系统的前向通道GB(s)和反馈通道H B(s)为:
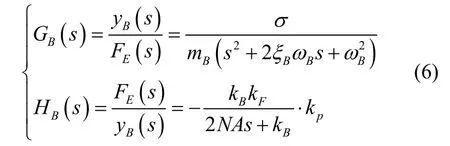
其中,ξB为桥梁模态阻尼,ωB桥梁模态频率。当不考虑支撑梁的弹性,电磁浮力FE(s)到电磁铁的垂向位移y E(s)的传递函数为:
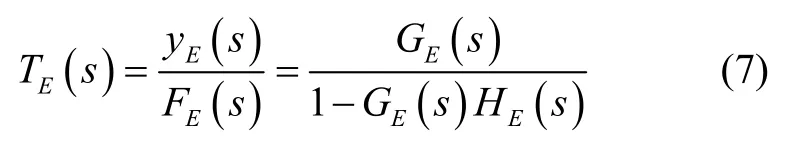
将式(5)代入式(7),其特征多项式ΔE为:
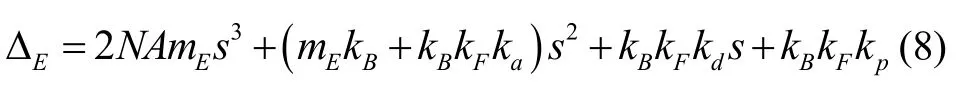
根据劳斯判据,当不等式(9)成立时,电磁浮子系统是稳定的。

考虑支撑梁的弹性时,对于磁浮列车-支撑梁耦合系统,电磁浮力FE(s)到支撑梁位移y B(s)的闭环传递函数为
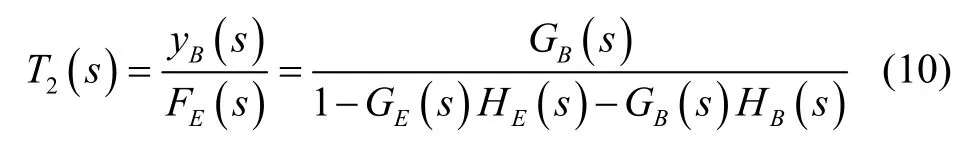
依据传递函数(式(10))可知,磁浮列车-支撑梁耦合系统的特征方程可整理为:
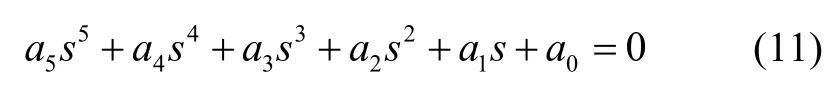

当kp=1000,kd=30,ka=0.4,kB=30,mB=2300,mE=1000,N=360,A=0.0184,kF=35295,ξB=0.005时,特征根的实部R1、R2、R3如图4 所示,在全频段,R2、R3均为负数,因此其稳定性取决于R1的情况。如图 4 所示,在[67.2rad/s 118.7rad/ s]区间,R1为正数,当支撑梁模态频率落在此区间时,极易引发振动问题。
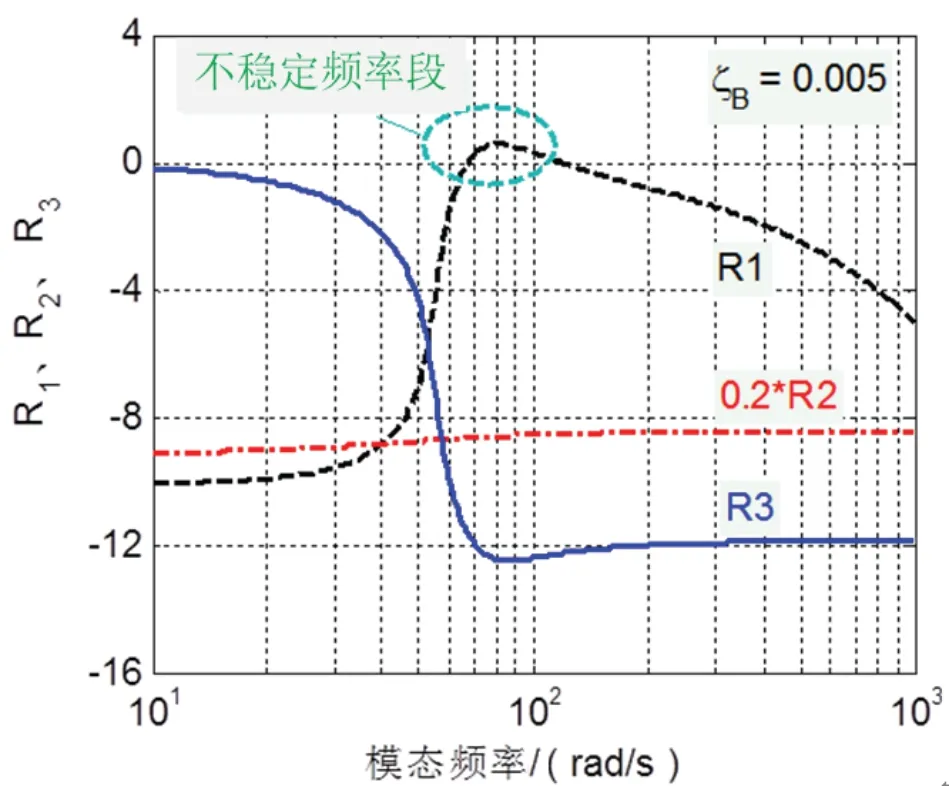
图4 特征根实部随模态频率变化图Fig.4 Diagram of real parts of characteristic root changing with modal frequency
3 控制算法优化
在如式(12)所示的状态反馈控制算法中,内环采用比例控制以提高系统响应速度。
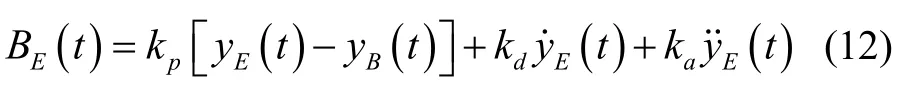
在准静态工况下,悬浮系统的跟踪能力要求较低,磁浮列车-支撑梁耦合系统的稳定性是考虑的重点。在这种情况下,期望磁通强度(式(12))可以写成:


图5 桥梁位移反馈增益为零时的系统框图Fig.5 System diagram when reducing the position control gain to zero
4 位置反馈信号重构
根据式(14)可知,期望磁通强度为电磁铁的垂向加速度、垂向速度和垂向位置的组合,与支撑梁的振动状态无关。实际工程中,悬浮电磁铁的位置信号不能直接测量,可利用刚性安装在电磁铁上的加速度计信号对电磁铁的位置进行估计[10]。理论上,电磁铁位置信号即加速度信号的两次积分,为消除两次积分的饱和效应,需要采用二阶自归零积分器代替二阶纯积分器,有:

当采用期望磁通强度(式(16))时,如图6 所示,桥梁子系统和悬浮子系统反馈通道的传递函数为:
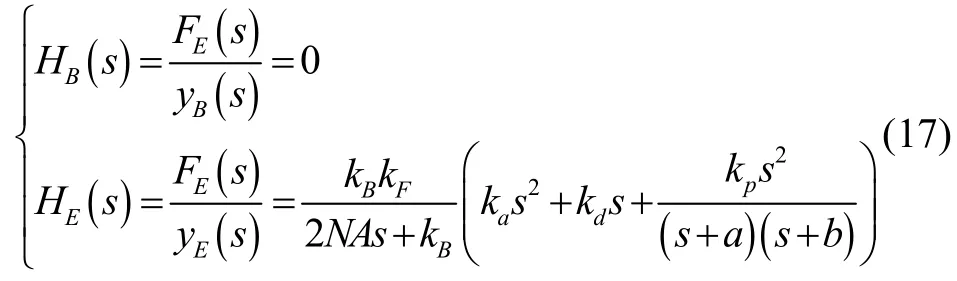
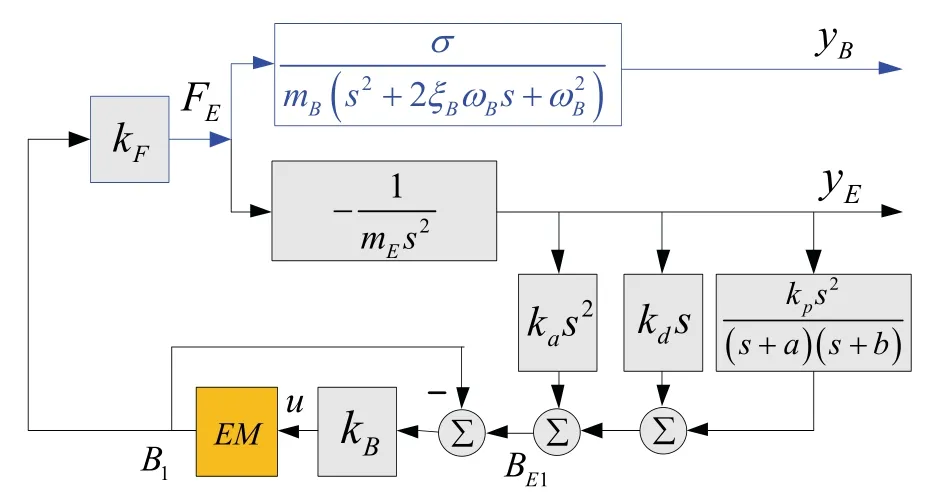
图6 利用加速度信号进行信号重构的系统框图Fig.6 System diagram when the position feedback are reconstructed by the acceleration signals
磁浮列车-支撑梁耦合系统的传递函数(式(10))为:
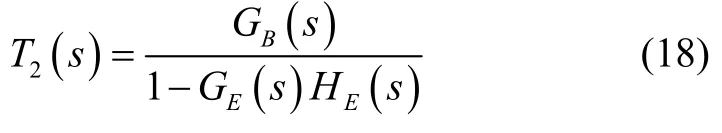
将式(5)(7)代入耦合系统的传递函数(式(18)),有:

根据上述分析,利用加速度信号对电磁铁位置信号进行重构和反馈,可以保证任意支撑梁下的稳定性。
5 仿真验证
利用加速度信号对电磁铁位置信号进行重构和反馈,为抑制耦合振动提供了一种解决方法。仿真采用全要素、非线性数值模型[11]。图7 给出了利用加速度信号进行位置重构控制的仿真验证。
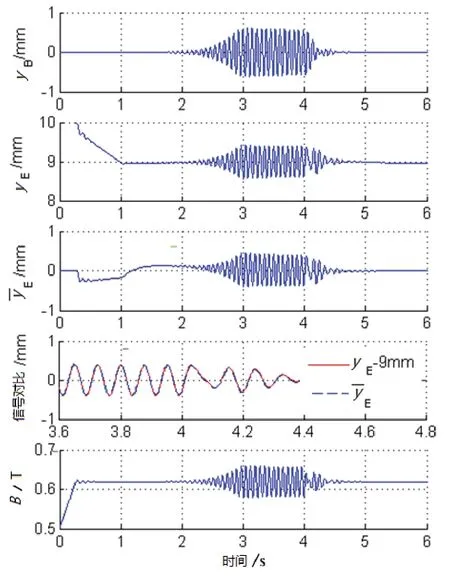
图7 利用加速度信号进行位置重构控制的仿真Fig.7 Simulation results when the position feedback are reconstructed by the acceleration signals
当时间t<4s 时,系统采用传统的基于磁通内环的状态反馈控制率,耦合系统出现了内生的、持续的垂向振动。
当时间t=4s 时,基于加速度信号重构的位置信号参与反馈控制,4.5 s 后,耦合自激振动幅度衰减至零。
悬浮电磁铁位置信号y E(t)没有能直接测量的感知手段,因此需要合理估计悬浮电磁铁的位置信号。由图7 所示,除动态响应阶段,估计值能准确估计出其垂向位置信息。
仿真结果表明,利用加速度信号重构电磁铁垂向位置信号并进行反馈,能够保证耦合系统稳定性,避免内生、持续振动现象。
6 实验验证
为了充分验证利用电磁铁加速度信号重构电磁铁垂向位置信号控制振动方法在工程上的可行性,在北车集团的磁浮基地开展了相关实验。车辆空载重13 t,载荷重8 t,平衡点悬浮间隙为9 mm,磁浮列车悬停在道岔东边的18 m 跨距的混凝土梁上,混凝土梁的线密度约为2.0 t/m。
如图8 所示,在1 s 时刻,利用加速度信号重构位置信号进行反馈以后,支撑梁和电磁铁的振幅迅速衰减;在2 s 时,振动幅值由1 mm 降低至自然噪声0.1 mm 水平。为反向验证算法的可行性,在3 s 时,恢复原有状态反馈控制律,振动又开始出现,且幅值不断增大。此次实验证明,利用基于电磁铁加速度信号重构其位置信号,并进行反馈的算法,可实现磁浮列车-支撑梁耦合系统的稳定,消除自激振动。
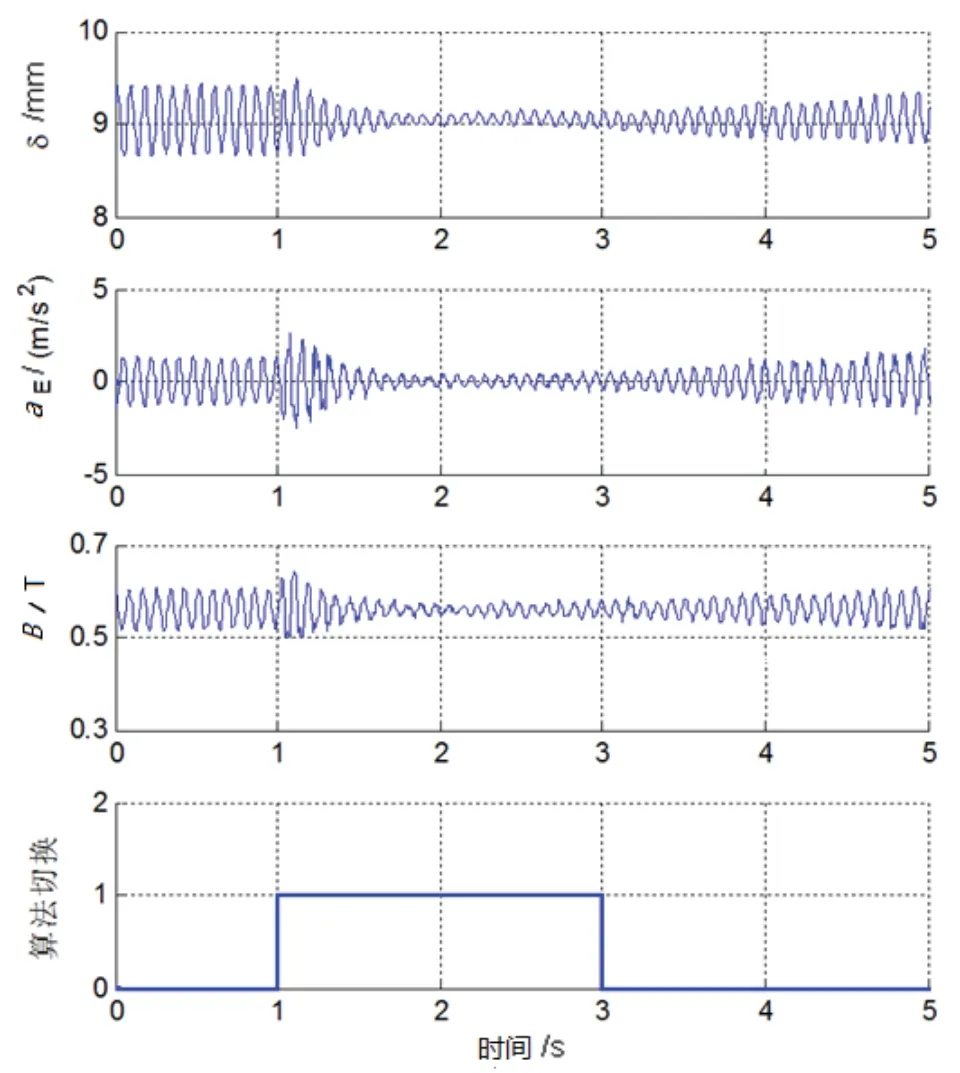
图8 利用加速度信号进行位置重构控制的实验Fig.8 Experiments results when the position feedback are reconstructed by the acceleration signals
7 结论
本文在借鉴磁浮列车-支撑梁耦合系统最小动力学模型的基础上,分析了采用磁通强度内环的系统框图特点和基于根轨迹的系统稳定性,提出了剔除桥梁位移反馈并采用电磁铁加速度信号重构垂向位置信号的控制方案,避免了磁浮列车低速式静止时的自激振动问题,开展了仿真和实验研究,验证了解决方案的可行性。
