液浮陀螺仪在双轴离心机上的标定方法

孙英博，任顺清，王常虹

（哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨 150001）

液浮陀螺仪凭其动态特性好、精度高、抗冲击振动能力强的特点被广泛应用于运载火箭、弹道导弹等远程航天系统中[1]。为了适应现代航天装备的精度需求，提高惯性平台系统中液浮陀螺仪的精度成为亟需解决的问题。受制造工艺的限制，提升液浮陀螺仪的制造精度需要革新的技术和高昂的成本。因此，通过深入研究其误差模型的标定方法和补偿方法是目前低成本且有效的提升精度的研究方向[2]。目前，液浮陀螺仪的误差模型标定方法主要分为重力场[3]和高G 环境的标定[4]。重力场标定主要通过高精度分度头、多轴转台[5,6]等设备进行。受激励程度的限制，陀螺仪误差模型中与比力相关的高阶误差模型系数不能被有效地激励，非线性系数不能被有效辨识会导致惯性平台的标定精度降低。因此，需要通过离心机[7,8]、振动台[9,10]等提供高G 测试环境完成非线性系数标定试验。由于陀螺仪主要敏感输入为角速度，因此离心机在旋转中引入的角速度输入会导致静态误差模型中与比力有关的系数无法精确辨识。当带反转平台的双轴离心机在主轴与方位轴同步反转时可以极大程度地规避离心机角速度输入的影响，同时提供高G 谐波比力输入。因此，带反转平台的双轴离心机在陀螺仪静态误差模型的高精度标定试验中应用较为广泛。

文献[11][12]分别分析了噪声和线振动台的周期性谐波误差对陀螺仪漂移误差系数标定的影响，但并未考虑线振动台的工具误差以及测试过程中产角振动产生的影响。文献[13]将工具误差及角振动进行了分析并提出了线振动台振动整周期的方法标定液浮陀螺仪。但是实际工程试验中低频线振动台试验虽然方法简单，但振动幅值稳定性、角振动误差等影响较大，对与液浮陀螺误差模型相关的高阶项标定精度影响较大，因此对于误差模型与比力相关的高阶项的标定，应考虑在带反转平台的双轴离心机上进行。文献[14]提出了一种利用速率转台旋转模式实现液浮陀螺仪误差模型各系数的标定方法，相对于多位置法提高了标定的效率，但试验采用的角速度率很小，不能呈现高G 试验环境。针对这个问题，文献[15]提出了一种在双轴离心机上采用十六位置法对液浮陀螺仪静态误差模型系数进行标定的方法，通过同步反转规避了角速率输入激励的同时实现了高G 的测试环境，充分地激励了高阶误差项，但文中并未考虑双轴离心机主轴和方位轴的旋转同步性对系数辨识精度的影响。

本文主要针对双轴离心机主轴和方位轴在速率追踪和相位追踪下旋转同步性的问题，分析两种跟踪模式下旋转不同步误差对液浮陀螺仪非线性系数与其相关漂移系数标定精度的影响。首先，对双轴离心机误差、陀螺仪安装误差等误差源进行分析；其次，分析离心机各轴系的误差传递关系，建立包含速率追踪和位置追踪不同步误差的双轴精密离心机误差传递模型；再次，结合误差传递模型，通过齐次变换准确确定输出激励的运动参数，并根据各项运动参数建立液浮陀螺仪误差模型。最后，根据误差模型通过仿真验证分析相位跟踪误差对液浮陀螺仪非线性误差系数标定的影响，并与传统的速率跟踪误差条件下标定精度进行对比分析，结果表明旋转不同步误差的大小影响标定精度的高低，在相位跟踪模式下，液浮陀螺仪的标定精度略高。

1 双轴离心机误差分析

1.1 双轴离心机结构

双轴离心机结构如图1 所示。其中1 表示离心机基座；2 表示离心机主轴轴线；3 表示离心机碳纤维大臂；4 表示激光干涉仪；5 表示离心机的水平轴轴线；6 表示离心机“鸟笼”反转平台；7 表示反转平台方位轴；8 表示液浮陀螺仪的安装位置。

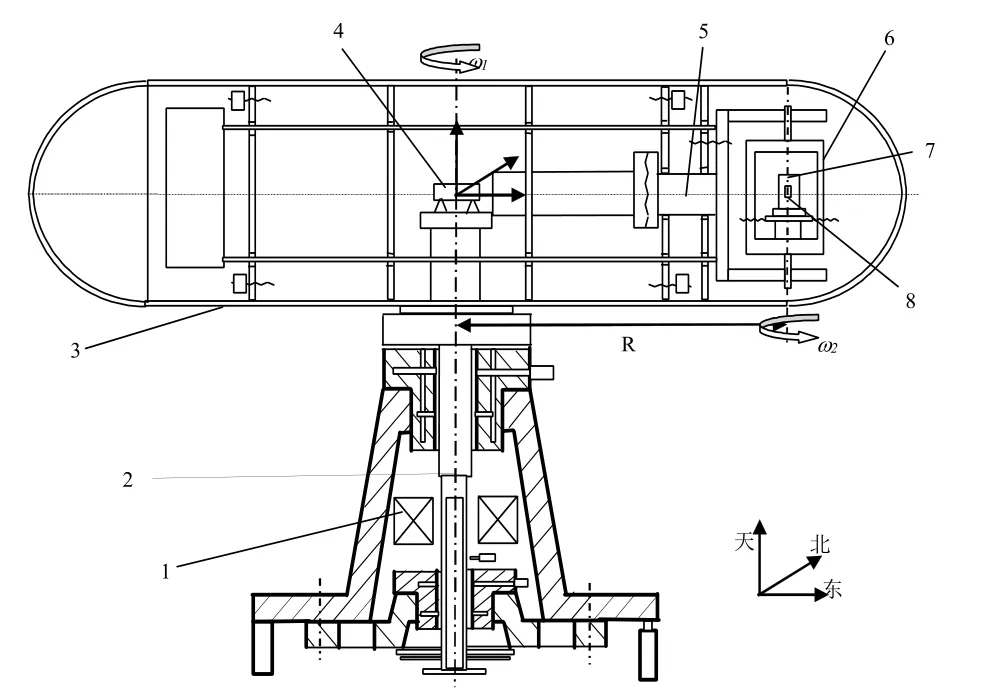
图1 双轴精密离心机结构示意图Fig.1 The diagram of the structure of the precision centrifuge

1.2 双轴离心机误差分析

对双轴离心机工作原理和结构分析建立如图2 所示的坐标系，并确定离心机各项误差源所在坐标系。依据各坐标系的转换关系，通过齐次变换可建立离心机主轴旋转角速度、方位轴旋转角速度、离心机位姿误差与液浮陀螺仪精密输入比力的内在联系。

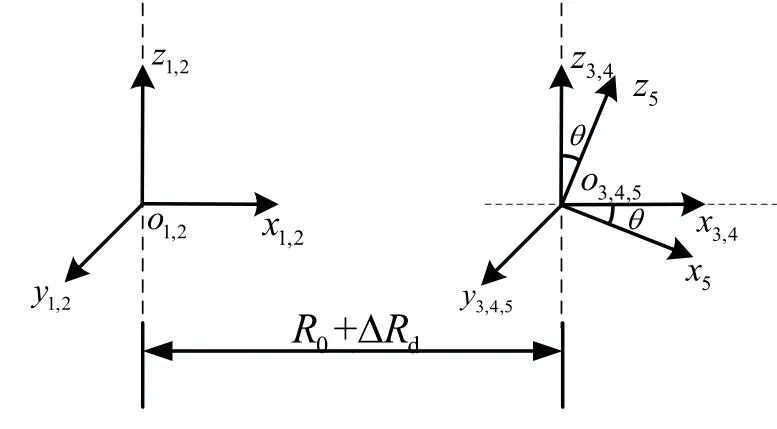
图2 双轴精密离心机坐标系示意图Fig.2 The diagram of coordinate systems of the precision centrifuge

本文主要针对旋转不同步误差对标定精度的影响，与离心机其他位姿误差不耦合，因此在坐标系的建立中只考虑旋转不同步误差。

坐标系建立如下：

（1）地理坐标系o1x1y1z1

地理坐标系为东北天坐标系，其中oz1与当地重力加速度方向平行，ox1指向水平东向，oy1指向水平北向，当地纬度为φ。

（2）主轴坐标系o2x2y2z2

主轴在旋转过程绕oz1轴旋转α，因此ox2y2z2相对于ox1y1z1的位姿矩阵为：

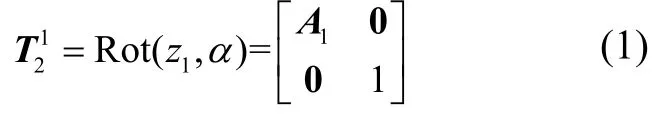
（3）水平轴坐标系o3x3y3z3

水平轴坐标系坐标原点o3相对于主轴坐标系原点o2距离为R=R0+ΔRd，其中R0为离心机半径标称值，ΔRd为在运行过程中干涉仪实时检测的动态半径误差。Δλy(ω)、Δλz(ω)为动态失准角，其大小与主轴角速度有关，可以表示为：

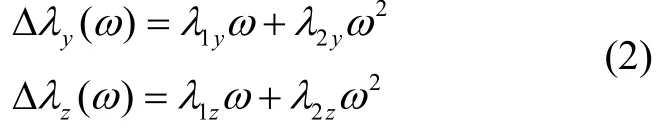
在试验中，通过双轴自准直仪可以检测动态失准角的变化，通过不同转速下的测试数据拟合可确定系数λiy、λiz的大小(i=1，2)，可以达到很高的拟合精度。o3x3y3z3相对于o2x2y2z2的位姿矩阵为：

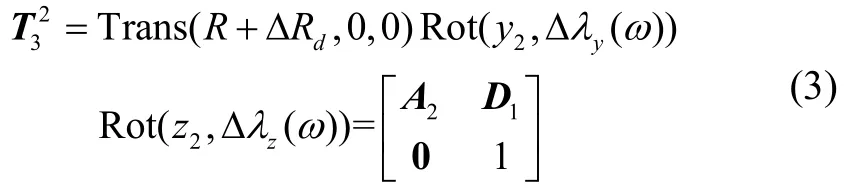
（4）方位轴坐标系o4x4y4z4

方位轴在与主轴同步反向旋转过程中绕oz3轴旋转β，主轴与方位轴存在平行度误差Δθx1、Δθy1，由于方位轴存在动不平衡晃动，可表示成一阶谐波形式展开为：

（5）陀螺仪坐标系o5x5y5z5

试验中，陀螺仪固定在反转平台的工装夹具上，夹具可以根据需求改变陀螺仪的姿态，相当于绕y4轴旋转θ，工装夹具的设计可以让陀螺仪质量重心和离心机旋转中心等高，相对于方位轴坐标系会存在偏心误差lx、ly。因此陀螺仪坐标系相对于方位轴坐标系的位姿矩阵为：

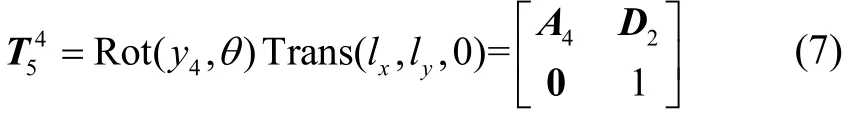
根据位姿传递的链式关系以及式(1)(3)(6)(7)，则陀螺仪坐标系相对地理坐标系齐次变换矩阵为：

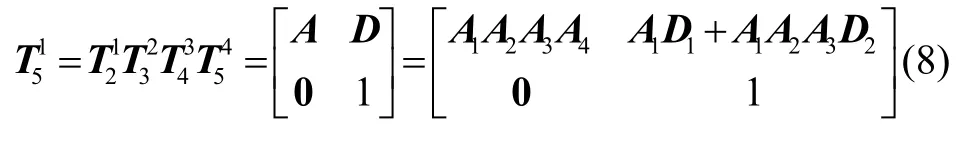
式中，A i表示各坐标系间的相对姿态矩阵；D i表示各坐标系间的相对位移矢量。

2 双轴离心机输出运动参数

双轴离心机JML-1 凭借其特殊的“鸟笼”结构的反转平台可运行位置模式和速率模式，本文所要标定的是液浮陀螺仪在高G 环境下误差模型与比力相关的各项系数，当存在角速度干扰时，会很大程度地影响标定结果，因此本文采用带反转平台的双轴离心机开展试验，主轴和方位轴同步反转时，陀螺仪各轴的指向保持不变，能够极大程度屏蔽掉测试过程中主轴旋转角速度的牵连运动对标定精度的影响。假设主轴旋转角速度为ω1，方位轴的旋转角速度为ω2，在同步反转模式下方位轴与主轴的角速度的理想关系为ω2=-ω1，但在实际系统中，主轴和方位轴的角速度不可能完全同步，角速度的不同步会在方位轴坐标系产生绕o4z4方向Δγ的角度误差。三种安装方式下的第一种安装姿态与方位轴坐标系相同，只存在偏心误差，其余两种姿态表示为绕o4z4轴顺时针与逆时针旋转45°，坐标系旋转矩阵A4对应改变即可获得最终的位姿转换矩阵。当双轴离心机主轴运行在方位轴同步反转模式时，陀螺仪的比力输入有3 个来源，分别是重力加速度比力、向心加速度比力和科氏加速度比力，陀螺仪的角速度输入为地球自转角速度分量，比力表达式如(9)所示。

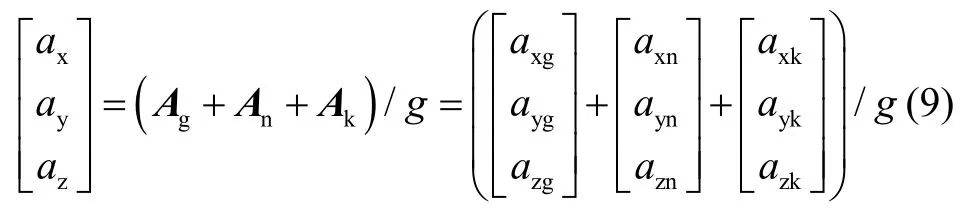
式中：Ag、An、Ak分别表示重力加速度比力、向心加速度比力、和科氏加速度比力在被测液浮陀螺仪的输入。

（1）重力加速度比力在液浮陀螺仪三轴上的分量

重力加速度产生比力在地理坐标系ox1y1z1中表示为[00g]T,根据位姿矩阵传递关系可得重力加速度在液浮陀螺仪坐标系表示：

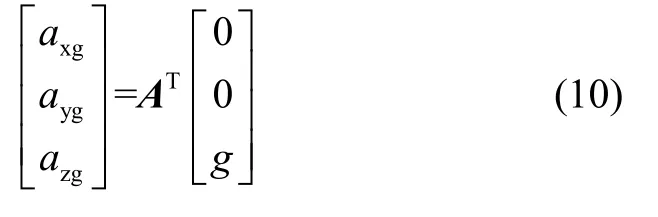
（2）向心加速度在液浮陀螺仪三轴上的分量

精密离心机运动产生的比力：

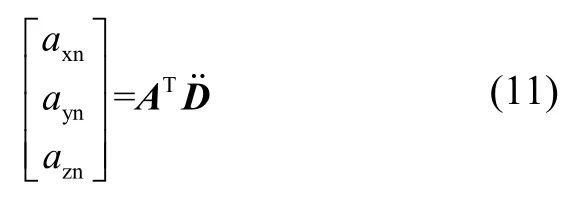
其中，A=A1A2A3A4，D=A1D1+A1A2A3D2。

（3）科氏加速度在液浮陀螺仪三轴上的分量

科氏加速度只与旋转轴系姿态矩阵有关，因此只需考虑主轴和方位轴，可得科氏加速度在液浮陀螺仪测试坐标系为：

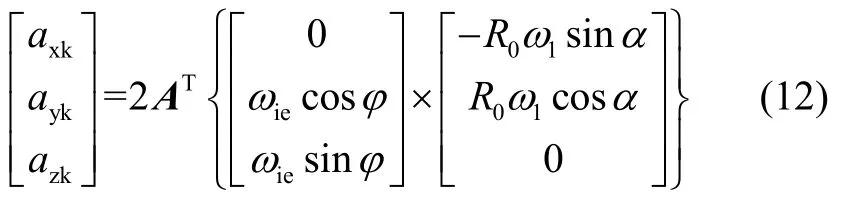
（4）地球自转角速度在液浮陀螺仪三轴上的分量

当双轴离心机运行在同步反转模式时产生了“消旋”现象，离心机的角速度被同步抵消，对输入信号的影响可以忽略不计，因此输入敏感角速度只有地球自转角速度分量：

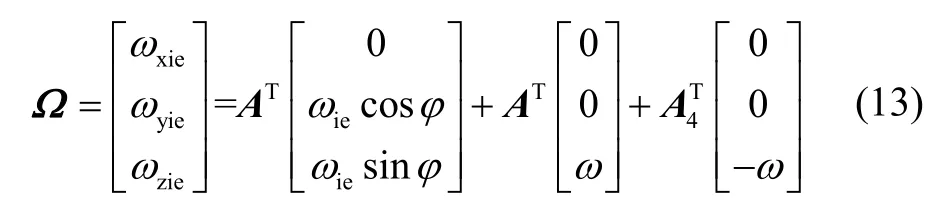
将式(9)-(11)代入式(8)中，可得双轴离心机同步反转模式下对被测液浮陀螺仪的精确三轴比力激励，将Ai(i=1,2,3,4)代入式(13)可获得三轴角速度激励，根据需求，化简规则为对于角速度输入保留至一阶小量，对于向心加速度、重力加速度、科式加速度输入保留标称值和与不同步误差γΔ 相关的项：

式中，φ为当地纬度，理想情况下α+β=0°，但在实际工程中，主轴和方位轴的速率存在不同步性，且速率追踪模式下角度的不同步会随着时间的累计逐渐增加，本文中采用Δγ=α+β表示主轴与方位轴旋转不同步误差。

3 液浮陀螺仪误差模型建立

参考文献[1]，液浮陀螺仪工程中常用的误差模型为：

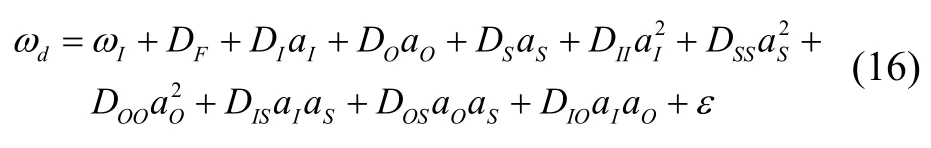
式中：ωd为陀螺仪的输出角速度，单位为rad/s；ωI为陀螺仪输入轴方向的角速度，单位为rad/s；D F为零偏，单位为rad/s；DI、DO、DS为三个轴向与加速度有关的漂移系数，单位为rad/s/g；DII、DSS、DOO为三个轴向与加速度二次方有关的漂移系数，单位为rad/s/g2；DIS、DOS、DIO为各个轴的加速度交叉二次项漂移系数，单位为rad/s/g；aI、aS、aO为输入轴、自旋轴和输出轴的比力输入，单位为g；ε为随机误差，单位为rad/s。

对于角速度输入，当双轴离心机同步反转时，三轴角速度输入包括地球自转角速度ωie分量和离心机角速度分量，由于陀螺对角速度较为敏感，因此化简过程中对于误差模型中含有三轴角速度分量的项均保留至一阶小量，其中ωie=7.292 ×10-5rad/s，作为一阶小量处理。对于比力输入，液浮陀螺仪对比力输入较不敏感，因此对三轴的比力输入保留至标称值，为研究角度不同步误差Δγ对辨识结果的影响，保留与Δγ相关的项。以第一种安装方式为例，液浮陀螺仪三轴的比力输入与式(15)对应为aI=a x,aO=a y,aS=az，角速度输入与式(14)对应为ωO=ω y,ωI=ω x,ωS=ωz，将各轴输入参数代入误差模型式(16)并化简可得：

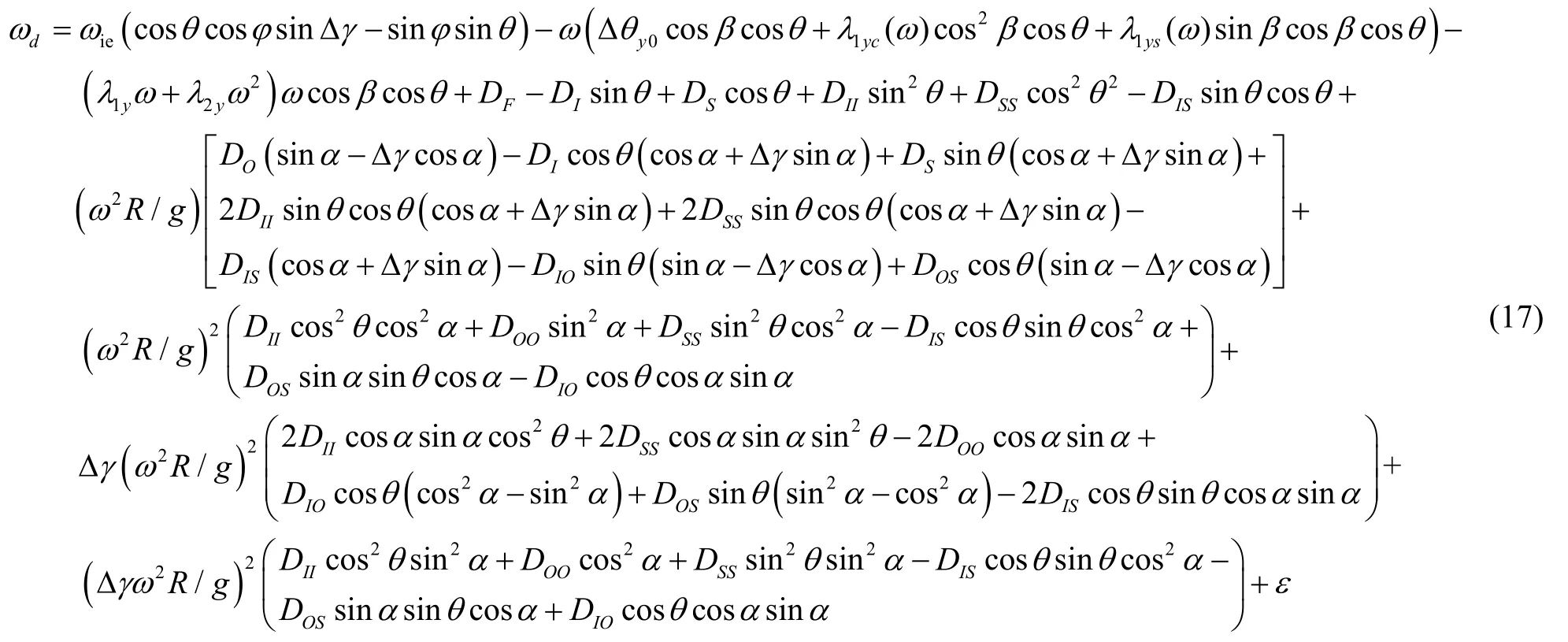
在实际液浮陀螺仪的标定过程中，采用离心机旋转整数倍周期的情况下，得到液浮陀螺仪旋转角度，再除以时间，得到平均角速度，以此作为观测量来标定液浮陀螺仪。在整周积分情况下，误差模型可写成：

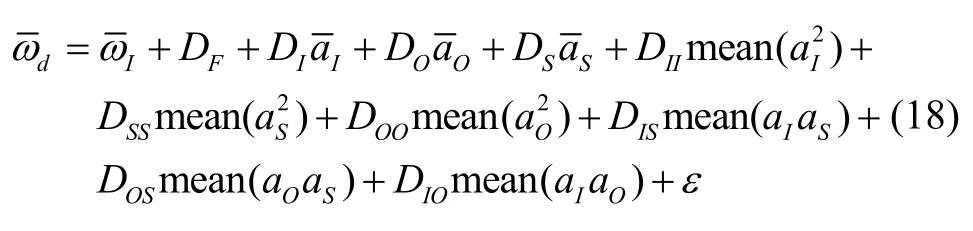
当主轴旋转圈数为n时，存在：

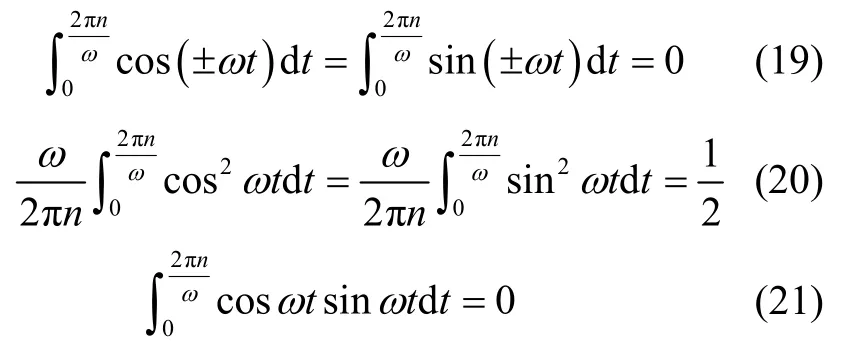
将式(19)-(21)代入(18)，误差模型变为：

可以看出，通过改变陀螺仪I、O、S轴的方向以及夹具的旋转角度θ来对误差模型中二次项误差系数进行辨识和标定。在实际系统中，方位轴相对于主轴转速控制采用速率追踪控制和相位追踪控制两种方式，不同的控制方式都存在轴系指向不同步的角度误差γΔ，试验表明，相位追踪控制时不同步角度误差为Δγp=2′，速率追踪控制时不同步角度误差每秒的累积量为Δγs=20.7′，目前现有的文献未曾涉及此类误差对参数辨识结果影响的分析，本文后面将给出分析。

4 液浮陀螺仪误差模型标定方法

本文针对实际工程测试使用的误差模型，设计了九位置法来标定陀螺仪二次项系数的试验方法，实现了对液浮陀螺仪误差模型全部高阶非线性误差项的有效辨识。液浮陀螺仪九种安装姿态如图3 所示。

图3 液浮陀螺仪安装方式Fig.3 Installation attitudes of the gyroscope

4.1 第一种安装方式

液浮陀螺仪第一种安装方式如图3(a)-(c)所示，输入轴方向平行于离心机的水平轴轴线，输出指向离心机半径切向，自转轴平行于主轴轴线。图3(b)与图3(c)分别为绕图3(a)中输出轴OA 方向正反转45°获得，由于第三节中模型建立采用与姿态一相同的坐标系指向，陀螺仪输出表达式如式(17)所示。式中当地纬度φ=45°。

为满足参数辨识要求，选取五种不同的采样角速度ωi(i=1,2...5)进行试验，采用等时间间隔采样，采样时长为主轴旋转100 圈，根据式(22)，将所有采样点的输出综合表示成矩阵形式，如式(23)所示。

对照式(22)，可简写为：

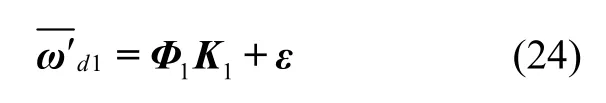
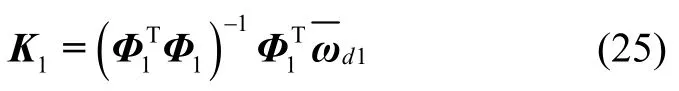
类似的，当θ=0°、± 45°时，第一种安装方式下的三种安装姿态的误差模型系数矩阵Ki(i=1,2,3)表示如表1所示。

表1 第1-3 种安装姿态的误差模型系数矩阵Tab.1 Error model coefficient matrices of the 1st-3rd installation attitudes

根据表1，可以看出二次项系数DIS和DSS可以通过加减解耦完成辨识。其余的二阶项需要结合其他两种姿态进行辨识。

4.2 第二种安装方式

液浮陀螺仪第二种安装方式的三种姿态如图3(d)-(f)所示，第二种安装方式相对于第一种的转换过程为先绕输入轴IA 顺时针旋转90°，再绕输出轴OA 顺时针旋转90°，自转轴方向平行于离心机的水平轴轴线，输入轴指向离心机半径切向，输出轴平行于主轴轴线。图3(e)与图3(f)分别为绕图3(d)中输入轴IA 方向正反转45°获得，将三轴的加速度激励分别与式(14)(15)对应并化简：

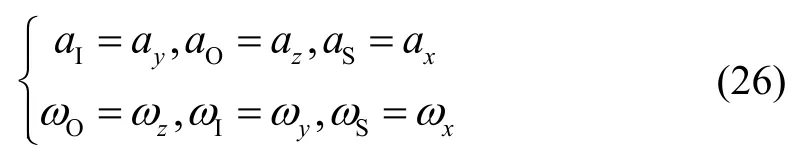
将式(26)代入式(17)中，可获得第二种安装方式的液浮陀螺仪输出表达式，与第一种安装方式类似进行整周积分并化简可得到平均角速度输出为：

表2 第4-6 种安装姿态的误差模型系数矩阵Tab.2 Error model coefficient matrices of the 4th-6th installation attitudes

4.3 第三种安装方式

液浮陀螺仪第三种安装姿态如图3(g)-(i)所示，第三种安装方式相对于第二种的转换过程为先绕自转轴顺时针SA 旋转90°，再绕输入轴顺时针IA 旋转90°。输出轴方向平行于离心机的水平轴轴线，自转轴指向离心机半径切向，输入轴平行于主轴轴线。图3(h)与图3(i)分别为绕图3(g)中自转轴SA 方向正反转45°获得，将三轴的加速度激励分别与式(14)(15)对应并化简：

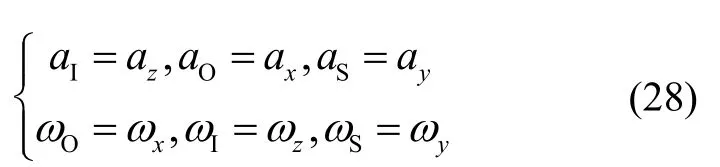
将式(28)代入式(17)中可获得姿态二的液浮陀螺仪输出表达式，与第一种安装方式类似进行整周积分并化简可得到平均角速度输出为：

表3 第7-9 种安装姿态的误差模型系数矩阵Tab.3 Error model coefficient matrices of the 7th-9th installation attitudes

表4 液浮陀螺仪误差模型系数辨识表达式Tab.4 Identification expressions of gyroscope’s error model coefficients

5 仿真校验与误差分析

本文所采用的精密离心机半径R为2.5 m，实验室所在纬度为φ=45°，g=9.8066m/s2。陀螺仪的指示输出值的不确定度独立且相等，为=10-8rad/s 。试验过程中，离心机主轴提供的角速度分别为ω1=4.43rad/s、ω2=8.85rad/s，相当于分别提供5g和20g的输入比力，采样频率为50 Hz，采用整周积分法数据采集。

由表4 可知各系数表达式，以DII为例可求解误差模型中各系数不确定度。DII的不确定度表达式为：

类似的，其他系数的不确定度计算如式(31)所示。忽略复杂的计算过程，得到各系数不确定度如表5 所示。

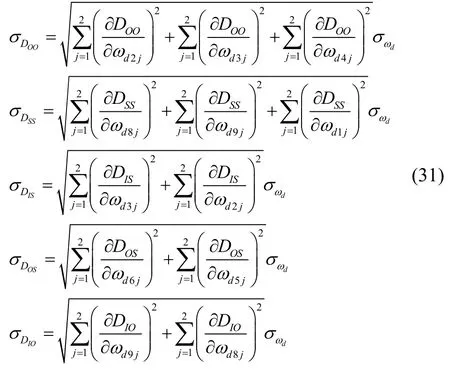
表5 液浮陀螺仪误差模型系数的不确定度Tab.5 Uncertainties of gyroscope’s error model coefficients

对于液浮陀螺仪，考虑参数如表6 所示。

表6 液浮陀螺仪误差模型系数设定值Tab.6 Values of gyroscope’s error model coefficients

对比表5 和表6，从数据可以看出，液浮陀螺仪误差模型二次项系数的辨识不确定度大小相对于系数本身均在0.2%以内，因此辨识结果满足置信度需求。

根据式(22)(27)(29)，将主轴两种输入角速度、姿态角、设定误差模型的参数设定值代入误差模型中，并加入模拟系统噪声3σ=1 ×10-7rad/s 的白噪声，可以获得陀螺仪的输出，根据前文所述辨识方法得到辨识结果如表7。

表7 液浮陀螺仪误差模型系数的辨识结果Tab.7 Identification results of gyroscope’s error model coefficients

对比表6 和表7，可以得到引入系统噪声对二阶项系数的影响，如表8 所示，通过标定结果的对比可以看出，本文的方法可以有效地标定陀螺仪的二阶误差项系数。

表8 系统噪声对误差模型参数标定的影响Tab.8 The Influence of system noise on the calibration of gyroscope’s error model coefficients

为了分析主轴与方位轴不平行度误差Δθy1和不同步的角度误差γΔ 开展对比试验，从式(22)(27)(29)中可以看出，通过整周积分的处理规避了动态失准角误差对误差模型输出的影响，但不平行度误差的一次谐波分量和γΔ 的存在会影响陀螺仪的输出，以式(22)为例，安装姿态为第二种，当ω2=4.42rad/s 时，不平行度误差的一次谐波分量产生的输出误差为7.11 ×10-6rad/s，对标定精度影响较大，相位追踪控制时不同步角度误差为Δγp=2′，速率追踪控制时不同步角度误差每秒的累积量为Δγs=20.7′，当Δγ达到1000′ 时，由Δγ引起的对输出的误差为1.823×10-7rad/s，相对于液浮陀螺仪的输出量级在2个数量级以内，会对参数的标定产生影响，因此设计对比试验，将九个姿态下的液浮陀螺仪输出中含有不同步的角度误差的分量进行补偿，并将补偿前的输出记为，将补偿后的输出记为，类似的，采用相同的辨识方法，将补偿不同步的角度误差后各参数辨识结果记为，同时，将不同步的角度误差参数辨识结果差值记为ΔDi，以DII为例，补偿前后的辨识误差如式(32)所示。

对比试验中，将不平行度误差的一次谐波分量和不同步的角度误差产生的输出误差进行消除，不平行度误差Δθy1为5 ×10-6rad/s，对于不同步角度误差Δγ，分别取Δγ1=200′和Δγ2=1000′，将不同步误差带来的有害误差输出误差消除后采用相同的辨识方法可得辨识结果如表9。

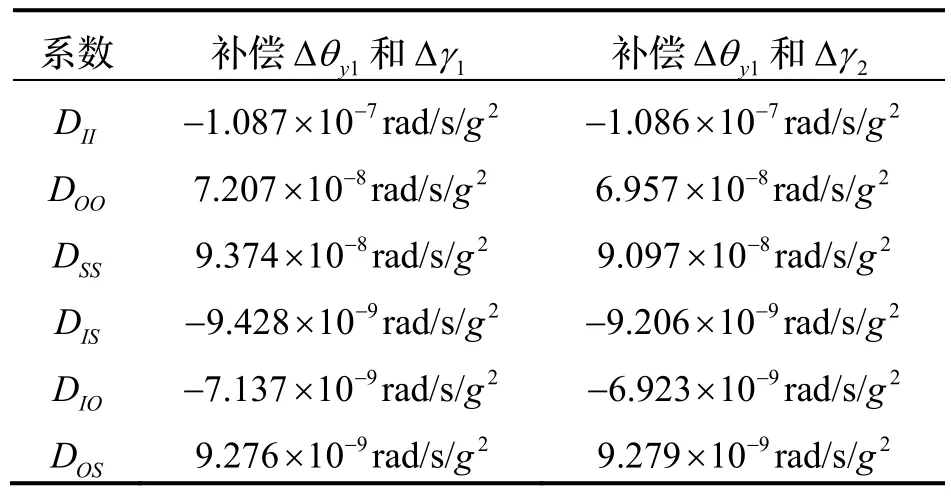
表9 液浮陀螺仪误差模型系数的辨识结果Tab.9 Identification results of gyroscope’s error model coefficients

表中，对比表6 和表9，可以获得两组不同的不同步角度误差对二阶参数辨识结果差值ΔDi，标定结果的精度为辨识结果差值相对于二阶参数百分比ΔDi/Di，标定结果精度如表10 所示。

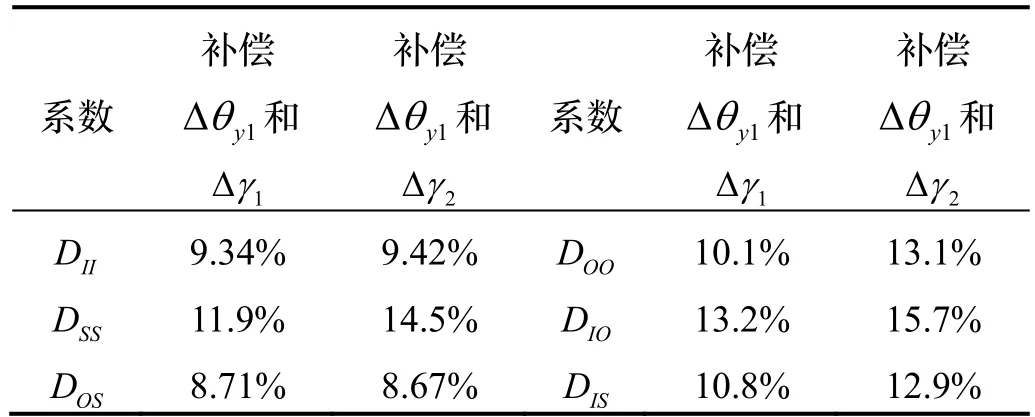
表10 液浮陀螺仪误差模型系数标定精度Tab.10 Calibration accuracy of the gyroscope’s errormodel coefficients

当Δγ1=200′时，产生的输出误差量级为10-8，相对于Δθy1的误差量级较小，标定精度主要受Δθy1的影响，从表10 可以看出，平行度误差Δθy1对标定精度的影响较大。随着不同步角度误差Δγ的增大，主要影响DSS、DOO、DIO、DIS的标定精度，对DII、DOS的影响很小。因此，在陀螺仪标定试验中对平行度误差和不同步角度误差Δγ补偿很有必要。对于Δγ，现有的试验设备多采用的是速率追踪，速率追踪控制时不同步角度误差每秒的累积量为Δγs=20.7′，随着时间的累计，误差累积速度较快，为此，考虑相位追踪的控制方式，相位追踪不同步角度误差可以达到Δγp=2′，大大降低了误差累计速度，提高二阶参数标定结果的精度，因此，在试验设备上采用相位追踪的控制方法是十分必要的。

根据上述误差分析，相对于传统的误差模型辨识方法，本文在传统的误差模型基础上引入了平行度误差和离心机不同步角度误差，分析了二者对误差模型二阶参数标定结果的影响，并说明了对新研发的试验设备采用相位追踪控制方法的必要性。在误差模型标定方法的设计中，采用了整周积分的数据处理方法，较现有方法增加了采样的数量，便于进行数据处理并可以消除地球自转角速度以及部分离心机误差对输出的影响，在一定程度上提高了误差模型系数辨识的精度。

6 结论

(1) 由于双轴精密离心机能够产生近零角速率、无比力梯度的高G 谐波加速度，并且近零角速率输入使离心机误差对陀螺仪与比力相关误差系数的标定精度影响很小。本文从目前工程上实际问题出发，相较于传统误差标定模型，着重考虑了动态失准角、主轴和方位轴的平行度和角度不同步误差对液浮陀螺仪输入运动参数的影响，并根据运动参数建立了完整的加速度计误差参数标定模型。

(2) 在数据采集与处理中，相较于传统的等时间间隔采集各个单点数据，改用整周积分的数据采集方式，增大了采集的数据量，提高了采样数据的可靠性，降低了数据处理的难度，进而提升误差模型标定结果的可靠性。

(3) 本文针对整周积分后的误差模型设计了相应的九姿态标定方法，相较于传统的十六姿态标定法，在满足标定精度的前提下大幅减少了姿态改变次数，提高了标定效率，同时，本文实现了陀螺仪误差模型二阶项系数的独立辨识，规避了离心机误差对参数辨识精度的影响。

(4) 本文通过仿真验证了二阶误差项系数的辨识精度，分析了各项误差系数辨识的不确定度，并分析了平行度和不同步角度误差的大小对各系数辨识结果的影响，误差模型系数辨识的精度可控制在模型系数的13.2%以内。对于不同步角度误差，在相同试验时长下，相位追踪控制方法相对于传统的速率追踪控制方法误差累计速率大大降低，相位追踪模式能有效降低角位置不同步误差对标定结果的影响。