一种基于自激励的核磁共振陀螺仪闭环控制方法
2022-12-16岳亚洲明泽额尔顿
岳亚洲,明泽额尔顿,雷 兴,张 昊
(1.西安飞行自动控制研究所,西安 710065;2.航空惯性技术重点实验室,西安 710065)
随着量子信息技术的进步以及原子自旋、原子干涉等理论的突破,高精度、高灵敏度的原子陀螺仪的出现,必将对未来的惯性导航与制导领域产生颠覆性影响[1,2]。核磁共振陀螺仪(Nuclear Magnetic Resonance Gyro,NMRG)是其中最具代表性的产物之一,基于原子自旋内禀属性,利用原子在恒定磁场下的宏观磁矩进动,通过自旋交换极化、磁场激励和进动检测等操作,实现对载体角速度的精确测量[3-5],是世界上已经实现的体积最小的导航级陀螺,为惯性导航带来了革命性的新手段[6,7]。
本文首先介绍核磁共振陀螺仪的基本原理,并对其中的闭环控制方法进行分析。针对传统方法存在的不足之处,在其基础上设计了一种新型的自激励闭环控制方法。利用仿真软件对方案建立数理模型,并设计实验,对新型闭环方法的零偏稳定性和角速率分辨率进行测试,最终验证了该方法的可行性与优势。
1 核磁共振陀螺及其闭环控制原理
当具有自旋磁矩μI的原子处于外加恒定磁场中时,会围绕外磁场的场线方向进行进动,可表示为[8]:

这种现象即核磁共振,式(1)中γ为原子核旋磁比,B0为恒定磁场强度。进动的频率ω0称为拉莫尔进动频率,可表示为:

如图1所示,在陀螺中建立空间直角坐标系,将竖直方向设为Z轴,沿该方向施加恒定磁场和圆偏振抽运光,使碱金属原子87Rb极化,并通过自旋交换碰撞将极化状态传递给惰性气体原子129Xe和131Xe,使Z轴方向上出现宏观极化磁矩M0。在X轴方向施加横向激励磁场B1cosωt,使XOY平面内出现绕Z轴进动的横向磁矩分量M⊥。在与激励磁场相同的方向上施加线偏振探测光,根据法拉第旋光效应,当载体相对惯性空间以角速率ωr绕Zω0轴转动时,探测光测得的进动频率ω可表示为式[9]:

图1 核磁共振陀螺的原理示意图Fig.1 Schematicdiagram of the principle of an NMR gyroscope

式中,ωr的正负取决于陀螺转动方向,若已知,可实现载体转动角速率的测量[10]。载体转动角位移的测量与之同理。
维持原子稳定共振的横向磁场闭环控制是核磁共振陀螺中的关键技术之一。目前通常采用基于相位锁定的闭环控制方法[11,12],如图2所示。采用两种惰性气体同位素作为工作介质,如129Xe和131Xe,在恒定磁场和激励磁场的作用下,两种经自旋交换极化的同位素原子以各自的进动频率绕Z轴进动。通过闭环控制,可使激励磁场的频率或相位实时跟踪进动信号,维持惰性气体原子的稳态进动,实现陀螺随载体相对惯性空间的转动角位移信息的提取。本地振荡器产生参考信号的相位φ2'=γ2B0t,经过相位比较器获取陀螺转动角位移α=φ2'-φ2。

图2 基于相位锁定的陀螺闭环控制方法[9]Fig.2 Closed-loopcontrol method of NMR gyro based on phase locking
核磁共振陀螺激励磁场闭环控制方案仍在不断改进,目前已较为成熟,近年来国内也出现了一些新的方法[12]。但采用现有方法的陀螺在转速分辨率方面仍有较大的提升空间,并且存在零偏稳定性较差、转速分辨率较低的问题,限制了核磁共振陀螺的应用范围。根据闭环控制原理分析,存在这些问题的主要原因是陀螺闭环中相位调节的过程存在延迟,无法实现实时补偿,且由于系统采样率受限于晶振频率,进而限制误差提取精度,造成较大的量化噪声。针对现有方法的不足之处,对基于相位锁定的闭环控制方法加以改进,设计一种新型闭环控制方法——自激励闭环控制方法,能够进一步改善陀螺性能。
2 传统闭环控制方法仿真分析
气室内极化的129Xe 原子在磁场中的动力学方程可用Bloch 方程描述为[13]:
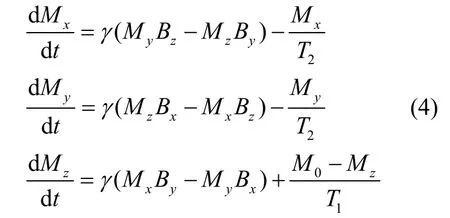
式中,T1和T2分别表示129Xe原子的纵向及横向弛豫时间,其取值影响宏观磁矩进动达到稳态的时间,通常在10s量级[14],故假定T1=10s,T2=5s。M0为稳态极化磁矩,经过理论分析与实验验证,取M0=1。[Mx,M y,Mz]T为气室内原子进动宏观磁矩即陀螺信号,[Bx,B y,Bz]T为外加磁场。γ取129Xe原子的旋磁比为11.86HzμT 。
为使得输出信号峰值达到最大,根据式(4),可解得最佳的横向磁场幅值为:
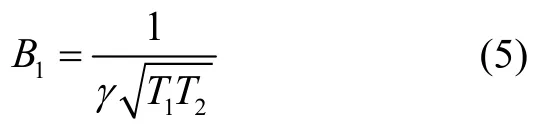
将γ、T1、T2代入式(5),解得B1=0.0019 μT。
利用数学仿真软件,搭建核磁共振陀螺磁场共振闭环的数理模型,如图3所示。输入不同形式的外界转速,即可模拟载体转角θ2的变化。

图3 核磁共振陀螺闭环仿真模型Fig.3 Closed-loopsimulation modelof NMR gyro
在仿真模型中,M0=1,工作物质129Xe旋磁比γ=11.86HzμT,横向磁场幅值B1=0.0019 μT,静磁场强 度Bz=10.12 μT,则工作点频率ω0=γBz=120Hz。弛豫时间T1=10s,T2=5s。仿真步长设定为10-5s。引入一个标准正弦参考信号参与到鉴相环节中,其相位设定为拉莫尔进动频率下的转角θ0。将鉴相结果θ1反馈至磁场信号产生模块中,并输入θ0及外界转角θ2,坐标变换后输出的磁场信号为:
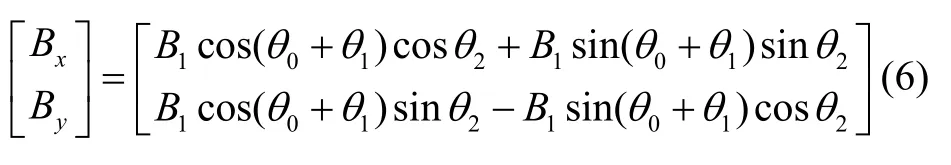
对闭环中鉴相环节的输出端进行监测,即可实现外界转速的读取。
将外界输入转速设定为0°/s,模拟静止状态下陀螺的转速输出,以便测量陀螺的零偏稳定性。仿真开始时刻记为0s,读取速度为1次/秒,在400s~4000s时间段内以100s的采样周期记录3600 个转速读取数值。仿真结果如图4所示,经计算,该闭环方法的零偏稳定性约为4.71°/h。
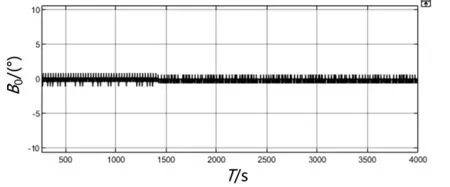
图4 传统闭环零偏稳定性仿真结果Fig.4 Simulation resultsof traditionalclosed-loopzero-bias stability
为检测陀螺转速分辨率,将外界输入转速设定为±1.0°/s,变化周期为10s。仿真输出结果如图5所示。该结果表明,采用传统闭环方法的陀螺可识别1°/s的转速,但其输出信号中存在较为明显的量化噪声。
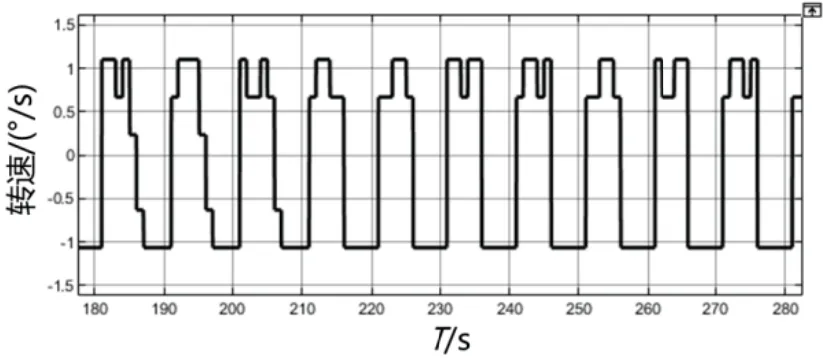
图5 传统闭环测量精度仿真结果(±1°/s)Fig.5 Simulation resultsof traditional closed-loop measurement accuracy (±1°/s)
经分析:量化噪声主要来源于陀螺误差提取环节。本文采用10-5s仿真步长,陀螺共振频率120Hz,相位误差有效刷新率为1/120s,为了避免由于闭环反馈速率慢导致的共振幅值扰动与相位误差之间的耦合,本文采用方波鉴相的方式进行误差提取,原子进动周期内能够鉴别的最小相位差为0.432°。这与图5中约0.5°的量化噪声一致。可以预见,若缩小仿真步长至10-7s,理论量化噪声将会降低至0.004°。但从仿真的角度看,仿真步长缩小意味着系统资源消耗变大。从实际应用的角度看,晶振时钟频率不可能无限提升。因此本文综合考虑,设置仿真步长为10-5s。
将输入转速幅值进一步缩小至±0.2°/s,仿真输出结果如图6所示。显然,对于采用传统闭环方法的陀螺,当输入转速的幅值在±1.0°/s以内时,输出信号中存在过大的噪声,使得陀螺无法准确读取外界转动信息。

图6 传统闭环测量精度仿真结果(±0.2°/s)Fig.6 Simulation resultsof traditional closed-loop measurement accuracy (±0.2 °/s)
3 自激励闭环控制方法仿真分析
根据上述仿真结果,采用传统闭环控制方法的陀螺的角速率分辨率低,分析其原因,误差主要来源为鉴相环节,对惰性气体原子进动信号进行解算后,作为反馈信号输入到磁场产生模块中,该环节不仅会引入误差,而且解算过程所需的时间也会导致反馈延迟,无法实时跟踪,进而无法实时补偿。
本文提出自激励闭环控制方法,其原理为:将陀螺启动阶段输出信号反馈至激励磁场线圈,利用原子核磁共振效应实现反馈,保持系统稳定。无需在外界施加独立横向磁场激励源,激励磁场来自于惰性气体原子自身的进动信号,经过移相、放大等适当处理,使其转化后满足激励磁场信号的条件,直接施加到激励磁场线圈。
根据该原理搭建自激励闭环控制方法的数理模型,如图7所示。
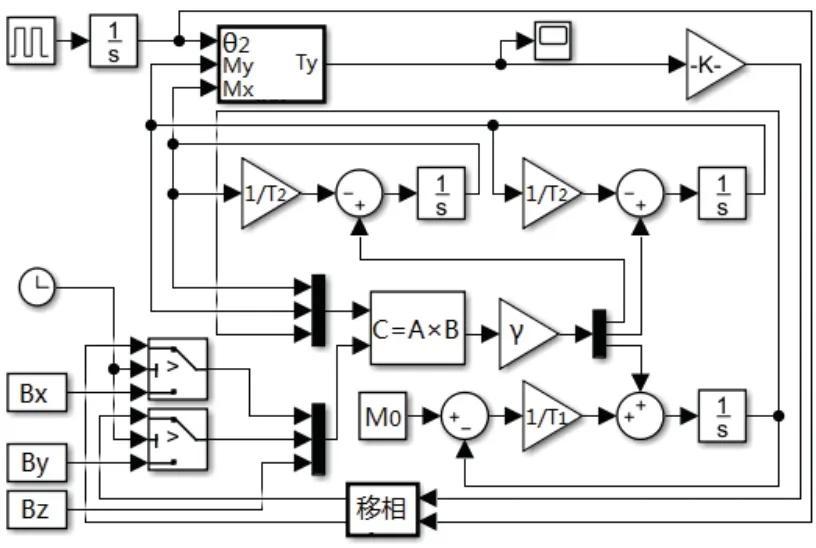
图7 自激励闭环仿真模型Fig.7 Self-excitation closed-loopsimulation model
仍将仿真开始时刻记为0s,启动过程中施加与前述传统模型中相同的激励磁场信号。对其输出信号波形进行监测。待陀螺运行至50s时,已达到稳定共振状态,之后对激励磁场输入端进行切换,断开横向激励信号源,将陀螺输出信号作放大、移相处理后,施加到激励磁场的位置。
陀螺输出的惰性气体原子进动信号可用式(7)描述:
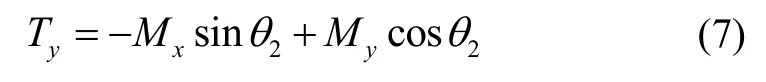
该信号的大小可以看作XOY平面上的总磁化强度在光电探测器轴向上的投影。陀螺具有外界转速时,为保持输出信号与输入磁场信号之间的相位差恒定,在移相环节中进行坐标变换,其输出信号可表示为:
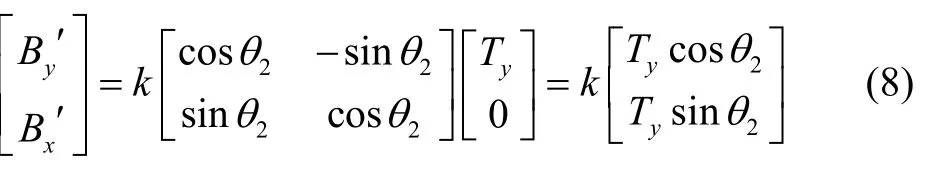
在式(8)中,k为放大倍数。根据共振信号波形,陀螺在稳定共振状态下输出信号的幅值约为0.35μ T,故最佳横向磁场幅值下将其放大倍数设定为k=2 ×0.0019/0.35 ≈1/92。
理论上,该方法避免了原有的鉴相环节导致的延迟,能够实现实时反馈,且反馈过程中的补偿参数由输出信号直接提供,能够进一步减小误差。
如图8所示,陀螺在50s之后输出信号幅值稳定,频率保持120Hz,仍可长期维持在共振状态。该结果表明,陀螺在采用自激励闭环控制方法时能够正常工作。
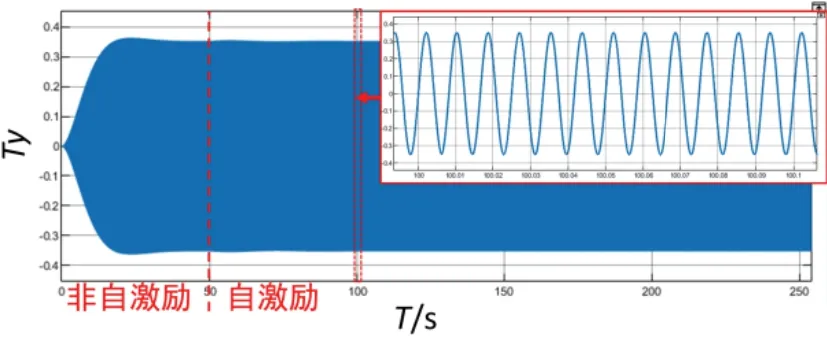
图8 自激励闭环控制下陀螺进动信号Fig.8 Gyro precession signalof self-excitation closed-loop control
在转速信息提取环节,采用相关解调,即陀螺进动信号Ty与120Hz 标准正弦参考信号相乘,以120Hz为周期对上述乘积进行滑窗累加求和获取陀螺角位移相位差信号,对角位移进行1s累加即可读取系统转速。该方法与传统闭环方案的转速提取相比,误差刷新率与晶振时钟一致,且综合考虑正弦波强度与相位的影响,相位分辨率更为精细,陀螺精度更高。传统闭环方案受制于其误差反馈方式,只能在一个进动周期内产生一个误差信号,因此并不适用本节中所采用的转速提取方案。
采用与前述非自激励模型相同的测试方法,在静态下测量陀螺的零偏稳定性,在动态下测量其转速分辨率。静态仿真测试结果如图9所示,经计算,采用自激励闭环方法的陀螺漂移约为9×10-4°/h,与传统方法的仿真结果相比,实现了极大地提升。

图9 自激励闭环零偏稳定性仿真结果Fig.9 Simulation resultsof self-excitation closed-loop zero-biasstability
动态仿真测试结果如图10-11所示,其中图10中输出结果对应的输入转速幅值为±1.0°/s,图11中输出结果对应的输入转速幅值为±0.1°/s。两种转速均可准确识别,输出结果无明显噪声,与传统闭环方法的读取结果相比,采用新闭环方法的陀螺显然具有更高的转速分辨率,可识别幅值在0.1°/s以内的更小转速。
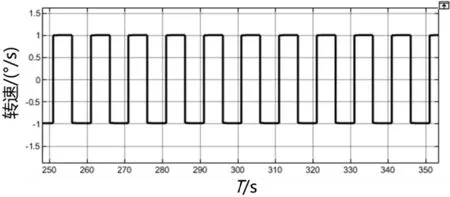
图10 自激励闭环陀螺测量精度仿真结果(±1°/s)Fig.10 Simulation resultsofmeasurement accuracy for self-excitation closed-loopgyro(±1°/s)
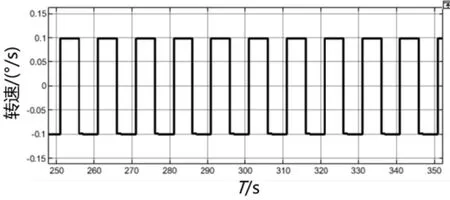
图11 自激励闭环陀螺测量精度仿真结果(±0.1°/s)Fig.11 Simulation results of self-excitation closed-loop measurement accuracy (±0.1°/s)
以上仿真结果从理论上证明了自激励闭环控制方法的正确性与优势。
4 自激励陀螺实验设计
为验证以上仿真结果,根据前述原理设计自激励实验装置,如图12所示。激光器的出射光分别为波长795 nm 的抽运光和波长780nm 的探测光,抽运光沿Z轴方向穿过气室。探测光经过适当的反射,沿X轴方向穿过气室,与线圈产生的激励磁场方向相同,垂直于抽运光的方向。偏振分光棱镜PBS将含有原子进动信息的探测光分为两束偏振方向相互垂直的线偏振光,二者分别通过光电探测器PD1和PD2转化为电信号,再经差分电路得到二者的差值,即Xe原子的进动信号。
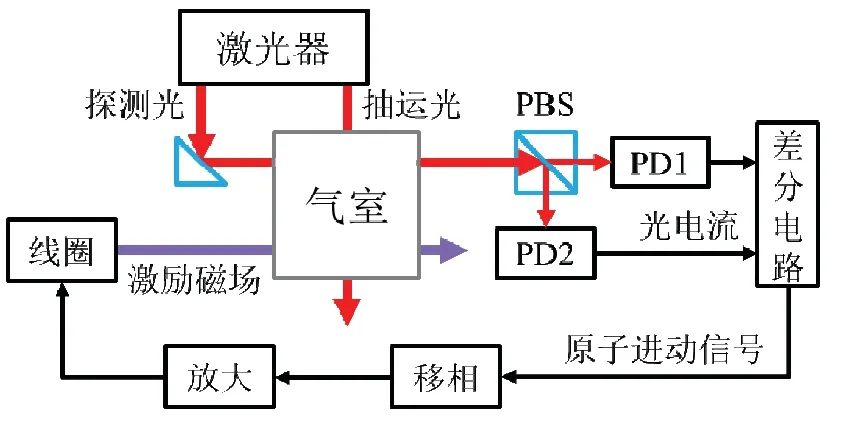
图12 自激励陀螺实验装置示意图Fig.12 Schematicdiagram of self-excitation gyro experimental device
图13为自激励陀螺实验设备,包括陀螺仪表头、激光器和自激励电路板。其中自激励电路板具备差分、移相、放大功能,输入端连接来自光电探测器的光电流信号,输出端提供的正弦交流信号可施加到磁场线圈中。

图13 自激励陀螺实验设备Fig.13 Self-excitationgyroexperimentalequipment
在相同的实验室环境下,分别采用传统非自激励闭环陀螺实验装置与上述自激励实验装置测试陀螺的零偏稳定性和测量精度。其中零偏稳定性实验结果如图14-15,经计算,传统闭环陀螺的零偏稳定性约为8.62 °/h,而自激励闭环陀螺的零偏稳定性约为0.39°/h。显然,自激励闭环方法显著提高了陀螺的零偏稳定性。
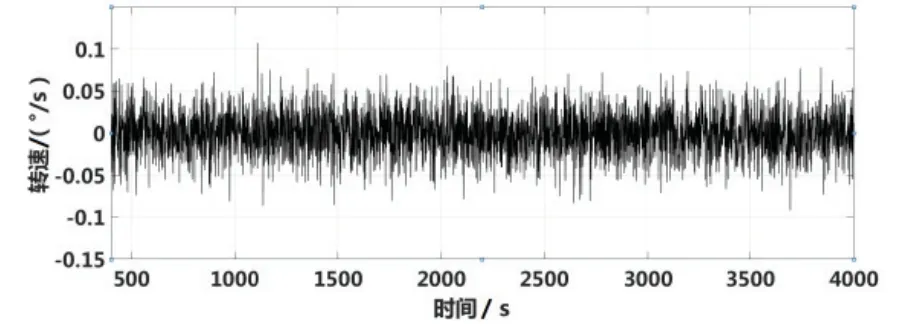
图14 传统闭环陀螺零偏稳定性实验结果Fig.14 Experimentalresultsof gyrodrift with traditional closed-loopcontrol
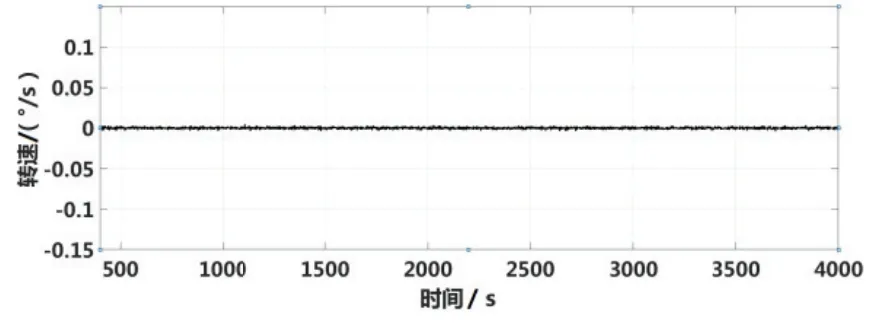
图15 自激励闭环陀螺零偏稳定性实验结果Fig.15 Experimentalresultsof gyrodrift with self-excitation closed-loopcontrol
测量精度实验结果如图16-17,分别输入±0.01°/s的转速,每次正转持续时间约50s,反转持续时间约50s,转动间隔约30s。根据实验结果,采用传统闭环方案的陀螺难以识别该转速,而采用自激励闭环方案的陀螺的读取结果较为准确。该结果进一步证明,自激励闭环控制方法能够有效提升核磁共振陀螺检测精度,助力陀螺性能提升。
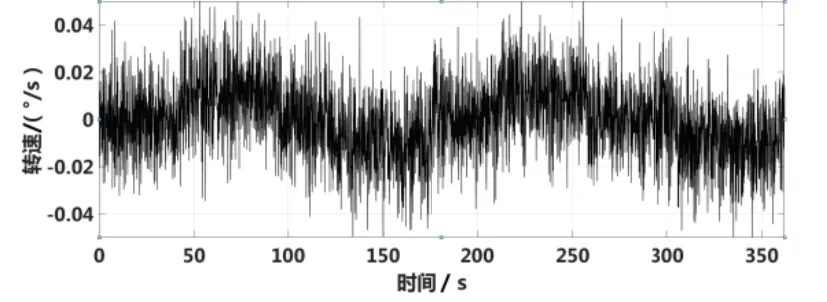
图16 传统闭环控制陀螺精度实验结果(±0.01°/s)Fig.16 Experimental resultsof gyroaccuracy with traditional closed-loopcontrol (±0.01°/s)
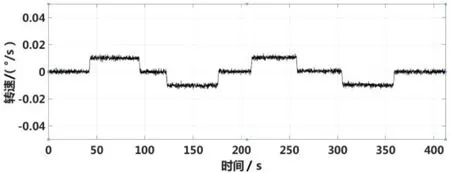
图17 自激励闭环陀螺精度实验结果(±0.01°/s)Fig.17 Experimental resultsof gyroaccuracy with self-excitation closed-loopcontrol (±0.01°/s)
以上实验中,检测系统的相位分辨率约为5×10-3°,在一定程度上限制了陀螺的精度。若要达到仿真模型中的精度,至少要求检测系统的相位分辨率达到0.28角秒,这需要通过提升工作气体弛豫时间以及降低所涉光源相位/功率噪声来实现。
与理论仿真不同,在实验过程中产生了一些由于陀螺系统连线/地磁/振动等因素导致的干扰,使得动态实验噪声略高于静态噪声,需要在今后的研究过程中提升陀螺集成度以及磁场补偿能力,保证陀螺精度进一步提升。
5 结论
经过理论计算、仿真分析与实验设计,自激励闭环控制方法的可行性已经得到验证。在数理仿真模型中,采用自激励方法的陀螺零偏稳定性高达9×10-4°/h,转速分辨率在0.1 °/s 以内,从理论上验证了该方法的正确性。在实验验证时,采用自激励控制方法的陀螺能够较为准确识别±0.01 °/s 的转速变化,且陀螺漂移约为0.39 °/h,与采用传统方法的陀螺(8.62 °/h)相比,精度提高了一个量级。
综上所述,本文设计了一种新型自激励陀螺闭环控制方法,具有更好的实时性和静态、动态特性,将载体的运动状态实时反馈给激励磁场,使得激励磁场根据相对运动的相位差进行调节。该方法能够有效解决反馈存在延迟、无法实时补偿的问题,进一步提升核磁共振陀螺的精度。此外,激励磁场由进动信号直接提供,不需要通过信号发生器持续产生,将会使核磁共振陀螺的结构进一步简化,有助于达到小型化的需求,未来将成为陀螺控制方面的重点研究内容。
