压力容器分析设计中等效应力的研究与探讨

2022-12-15白云波张亚宁袁继禹杜常宗

压力容器 2022年10期

白云波，张亚宁，袁继禹，杜常宗

(1.宁夏神耀科技有限责任公司，银川 750000；2.浙江大学，杭州 310007)

0 引言

压力容器分析设计的弹性应力分析方法中，等效线性化是选择合适的应力分类线，按照“静力等效”的原理，将应力沿分类线进行线性化等效应力处理，即用一个等价的线性化应力分布代替实际的应力分布。通过静力等效把各应力分量沿应力分类线分解为沿承压壳体壁厚方向均匀分布的应力(薄膜应力)、沿承压壳体壁厚方向线性分布的应力(弯曲应力)和非线性应力(峰值应力)[1-4]。

但是在工程实例中，经常发现某些计算出的应力分量是非线性或弯曲的，导致计算出的应力强度也会呈非线性。因此，采用应力线性化计算出的等效应力在某些情况下不一定代表真实的应力强度。很多专家学者对此进行研究并提出修正建议[5-7]。陆明万等[8]提出应力线性化出现错误的原因及修正建议；叶夏妮等[9]研究了应力线性化中横剪应力对应力强度的影响，提出应力等效线性化处理方法；黄勋[10]研究了应力线性化中不合适的应力选取会违反容器表面力边界条件，提出不违反边界条件的应力线性化修正方法。

本文按照ASME Ⅷ-2附录5.A.4应力积分法，对简单工程实例中应力线性化等效应力进行计算，探究等效应力线性化出现问题的原因，提出校核应力线性化结果时需要考虑的因素，避免出现错误。

1 ASME Ⅷ-2应力线性化基本原理

ASME Ⅷ-2附录5.A.4应力积分法，通过处理二维或三维连续单元有限元计算的应力结果，对沿应力分类线进行积分以确定薄膜应力和弯曲应力分量，再按照von Mises准则计算得到当量应力。计算步骤如下。

(1)计算薄膜应力张量。

薄膜应力张量是沿应力分类线每一应力分量的平均值组成的张量，或通过式(1)计算。

(1)

(2)计算弯曲应力张量。

①仅对局部周向和经向应力分量计算弯曲应力，并不对平行于SCL(应力分类线)的局部应力分量或面内的剪应力计算弯曲应力；

②仅对导致SCL扭转的剪切应力分布需要考虑剪切应力的线性部分(在垂直于周向平面中的面外剪应力)；

③弯曲应力张量是由沿应力分类线每一应力分量的线性变化部分所组成，或通过式(2)计算。

(2)

(3)计算峰值应力张量。

峰值应力张量是分量等于下值的张量：

σij,F(x)∣x=0=σij(x)∣x=0-(σij,m+σij,b)

(3)

σij,F(x)∣x=t=σij(x)∣x=t-(σij,m-σij,b)

(4)

(4)以薄膜和薄膜加弯曲应力分量为基础，计算在SCL端部处的3个主应力。

(5)以薄膜和薄膜加弯曲应力分量为基础，用von Mises理论计算在SCL端部处的当量应力。

按照ASME Ⅷ-2附录5.A.4应力积分法，用简单的回转壳体压力容器为例，对不同应力分类线的应力进行计算。

2 圆柱筒体远离结构不连续处当量应力计算

受内压P=10.0 MPa的回转壳体容器由圆柱筒体和沿轴线焊接在筒体两端的椭圆封头构成，其结构如图1所示。

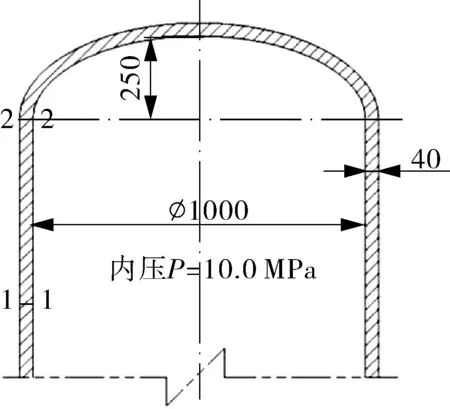
图1 受内压回转壳体压力容器结构示意

在圆柱筒体远离结构不连续处选取路径1-1作为应力分类线SCL1(应力分类线的选取按照ASME Ⅷ-2附录5.A进行选取，下同)，取与路径正交的一柱坐标系Orθz，径向、环向和轴向分别用r，θ，z表示。路径1-1上其中一点在坐标系Orθz中的应力状态如图2所示。

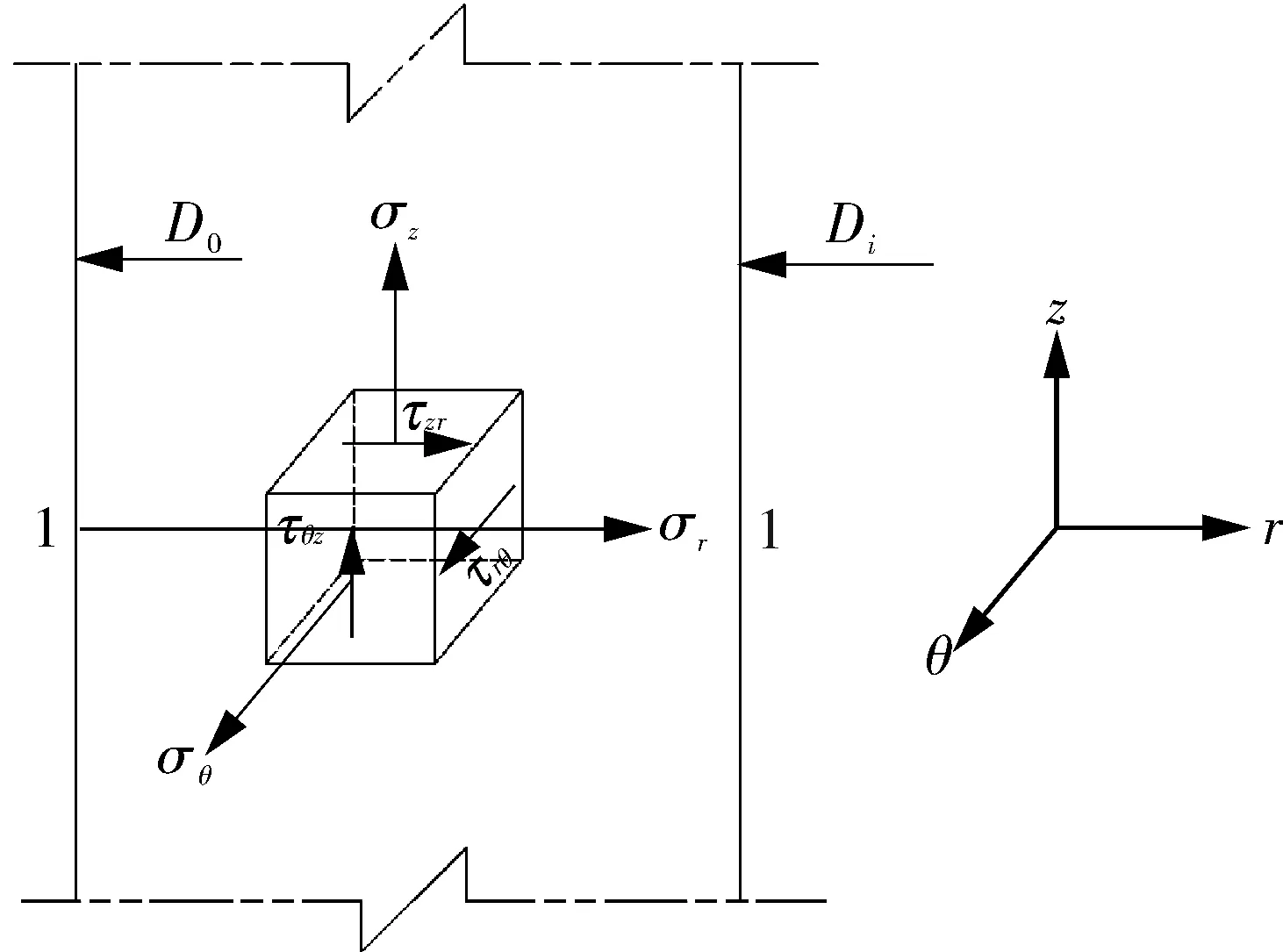
图2 SCL1上一点的应力状态

图2中，σr，σθ和σz是该点在坐标系中的正应力张量，τrθ，τθz和τzr是该点在坐标系中的剪切应力张量。因为沿应力分类线任何形式的应力分布经线性化处理后，最终的当量薄膜加弯曲应力必定出现在应力分类线两端，因此本例中按照拉美公式计算圆筒内壁一点的应力张量，其值如表1所示。

表1 圆柱筒体远离结构不连续处内壁应力张量

ASME Ⅷ-2附录5.A.4.1.2和JB 4732—1995《钢制压力容器——分析设计标准》中第4.6，4.7，4.8条都提出，薄膜应力的应力张量σr，σθ，σz，τrθ，τθz，τzr都应当线性化。弯曲应力仅考虑垂直于所考虑截面/路径的应力分量，因此并不对平行于应力分类线的σr，τrθ，τzr正应力或面剪应力计算弯曲应力，即令其弯曲应力值为0。

因此，按照即ASME Ⅷ-2附录5.A.4中第(1)～(3)步计算并提取该点的薄膜应力、弯曲应力、峰值应力和薄膜加弯曲应力张量如表2所示。

表2 圆柱筒体远离结构不连续处内壁薄膜、弯曲、峰值和膜加弯应力张量

该点的剪应力τrθ，τθz，τzr与正应力σr，σθ，σz相比是一个小量，可以略去(可参考分析设计标准JB 4732—1995第5.2.4条注1)。因此，薄膜应力、薄膜加弯曲应力的主应力σ1=σθ，σ2=σz，σ3=σr，即ASME Ⅷ-2附录5.A.4中第4步中所需的3个主应力。

最后，用von Mises理论计算得到该点的当量应力，即ASME Ⅷ-2附录5.A.4中第(5)步。

至此，SCL1靠近内壁的当量应力计算完毕。该点处薄膜应力为112.43 MPa是一次总体薄膜应力，薄膜加弯曲应力为116.78 MPa是一次薄膜加弯曲应力，分别根据当量应力性质的不同，采用等安全裕度的原则选取不同的许用极限，结合所用材料的许用应力校核结构的安全性。

工程实例中，仅承受内压的圆柱筒体远离结构不连续处的壁厚和薄膜应力可直接用公式计算。以上计算过程只用来描述ASME Ⅷ-2附录5.A.4应力积分法计算应力分类线等效应力的一般方法。

3 结构不连续处的等效应力线性化

仍以上述压力容器为例，在其壳体与椭圆封头的结构不连续处选取路径2-2作为应力分类线SCL2，取与路径正交的一坐标系Orθz，径向、环向和轴向分别用r，θ，z表示。路径2-2上其中一点在坐标系Orθz中的应力状态如图3所示。

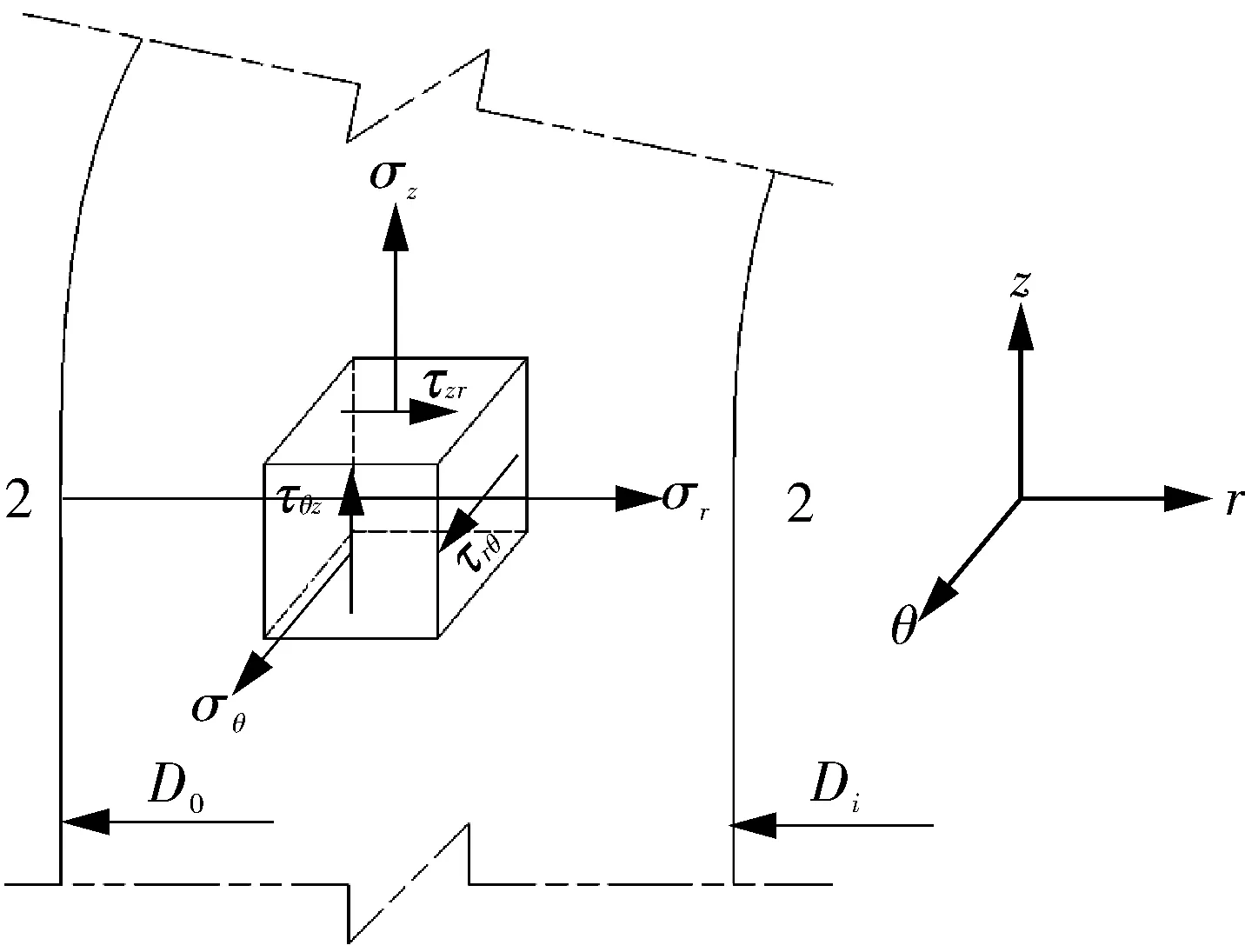
图3 SCL2上一点的应力状态

按照承受内压的标准椭圆封头计算方法[11]对封头与筒体连接处的应力进行计算，为了便于对比，本计算也提取应力分类线靠近内壁一端的点应力张量，其值如表3所示。

表3 圆柱筒体靠近结构不连续处内壁应力张量

按照ASME Ⅷ-2附录5.A.4中第1,2,3步计算并提取该点的薄膜应力、弯曲应力、峰值应力和薄膜加弯曲应力张量如表4所示。

表4 圆柱筒体靠近结构不连续处内壁薄膜、弯曲、峰值和膜加弯应力张量

可见该点的剪应力张量τzr与正应力σr，σθ，σz大小相当，不能按照前述方法进行略去，否则计算结果会出现错误。可以根据应力张量的分解与不变量[12]，计算该点薄膜应力、薄膜加弯曲应力状态下的主应力和主方向。计算该点薄膜加弯曲应力状态下的主应力和主方向过程如下：

(5)

主应力的求解可以用下面的方程：

σ3-J1σ2+J2σ-J3=0

(6)

式(6)为应力状态的特征方程，它的3个根即为所求的3个主应力。J1,J2,J3为应力不变量，其计算公式为：

J1=σθ+σz+σr

(7)

(8)

(9)

主方向与路径正交一坐标系夹角为：

(10)

其中：

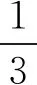
(11)

(12)

(13)

由式(6)(10)，即可计算ASME Ⅷ-2附录5.A.4中第4步中所需的3个主应力，再用von Mises理论计算得到该点的当量应力，即ASME Ⅷ-2附录5.A.4中第5步。该点薄膜加弯曲应力状态下的主应力张量、主方向和当量应力如表5所示。

表5 圆柱筒体靠近结构不连续处内壁薄膜、膜加弯主应力和偏斜角度

由表5可以看出，对于结构不连续处的应力进行线性化时，其计算出的主应力张量和应力分类线产生了偏斜(见图4)。

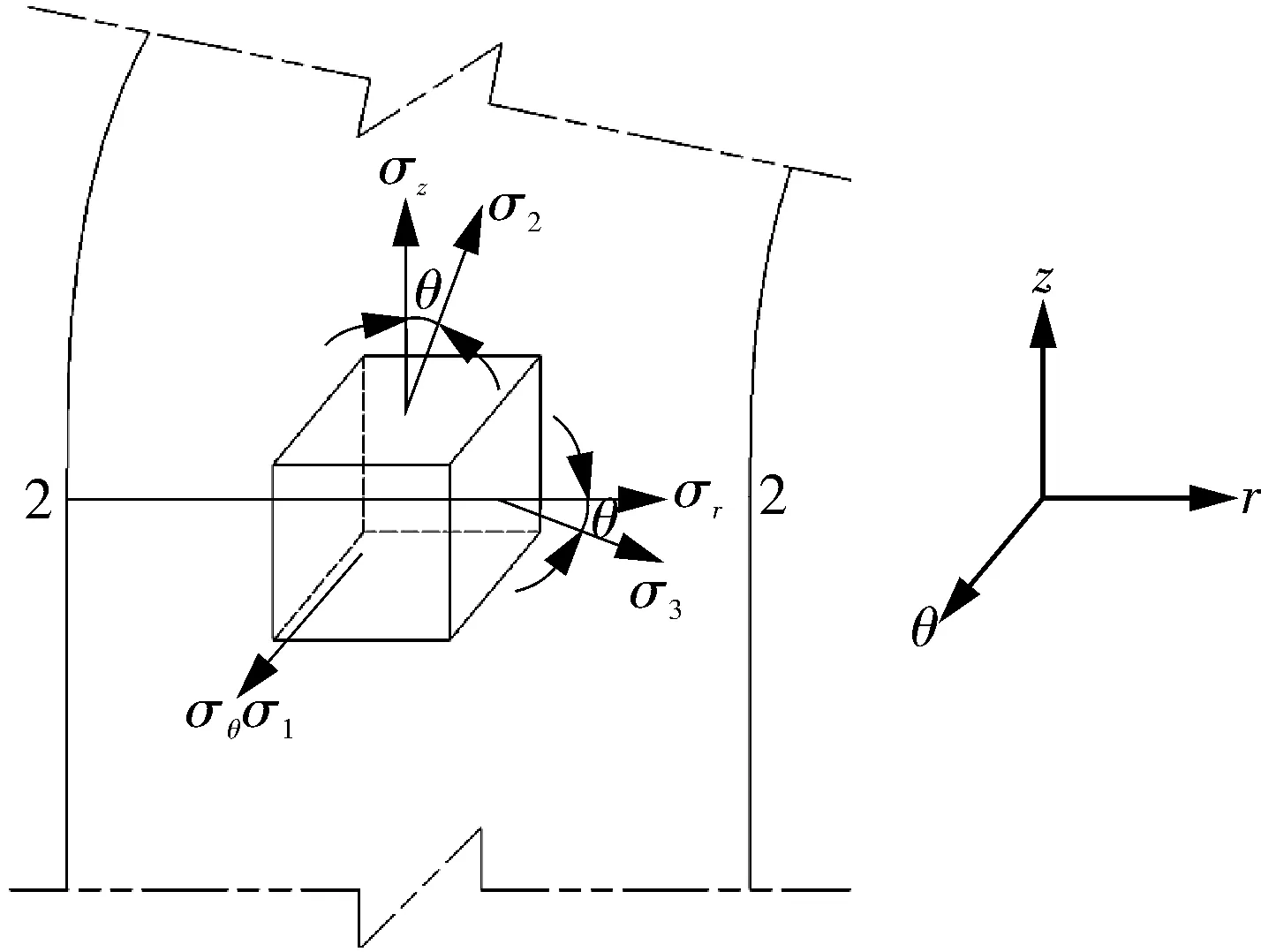
图4 SCL2上一点的主应力张量和分类线产生偏斜示意

压力容器中，除壳体特别薄或远离结构不连续处以外，应力沿壁厚大都呈非线性分布，沿应力分类线的应力张量有正应力和剪应力，因此主平面和应力分类线正交的坐标系存在夹角。根据标准规范的规定，对于在选择的线上只有与线垂直的应力分量才有弯曲的物理意义，但是对计算出的主应力在分类线正交的坐标系中的分量是否进行分解且进行线性化处理，ASME Ⅷ-2和JB 4732—1995未做明确的规定。

因此，本例在计算当量应力时，不再对计算出的3个主应力进行坐标系分解处理，直接用von Mises 理论计算该点的当量应力，即ASME Ⅷ-2附录5.A.4中第5步。对于该点来说，计算得到的该点处薄膜应力为59.91 MPa是局部薄膜应力，薄膜加弯曲应力为95.13 MPa是二次应力。可根据当量应力性质的不同，根据不同失效模式制定的失效准则，结合所用材料的许用应力校核结构的安全性。

4 有限元软件计算对比

对于圆柱筒体远离结构不连续处当量应力计算，有限元软件计算结果与手动计算结果虽然略有区别但相差不大。但是对于结构不连续处的当量应力计算，两者之间出现了较大的差异。

下面通过提取结构不连续处的应力，对有限元软件计算过程及产生差异的原因进行分析。有限元软件中柱坐标系OXYZ，径向、环向和轴向分别用X，Z，Y表示。有限元软件计算的SCL2应力分类线靠近内壁端点处的应力如表6所示。

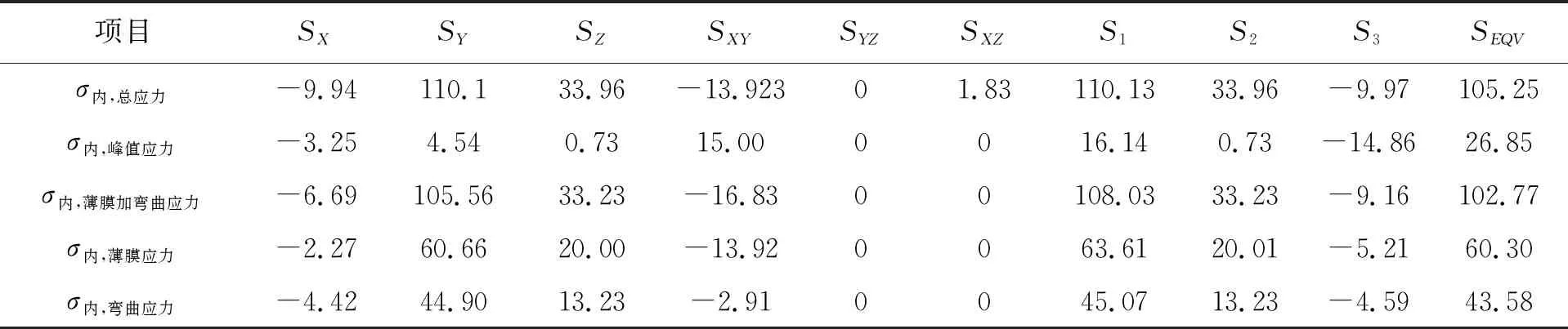
表6 有限元软件计算的圆柱筒体靠近结构不连续处内壁薄膜、弯曲、峰值和膜加弯应力张量、主应力及其当量应力

由表6可以看出，有限元软件计算弯曲应力时，对平行于分类线的SX,SXY，SXZ正应力和剪应力仍计算弯曲应力，没有按照ASME Ⅷ-2附录5.A.4.1.2和JB 4732—1995第4.6，4.7，4.8条的规定，令其弯曲应力值为0。并且与手动计算一样，也未对计算出的主应力在分类线正交坐标系中的分量进行分解。两种方法计算的薄膜应力、薄膜加弯曲当量应力如表7所示。